滴线区原子核第一性原理Gamow壳模型研究

2023-08-31耿一方许甫荣

核技术 2023年8期

张爽耿一方许甫荣

（北京大学物理学院核物理与核技术国家重点实验室北京 100871）

新一代放射性核束装置的建成，为远离稳定线的原子核性质的研究开拓了广阔的场景［1-3］。位于核素图边界的原子核陆续被合成，并且这些原子核显示很多奇特现象，例如：核子发射［4-6］、晕结构［7］、壳演化［8］及Thomas-Ehrman shift（TES）［9-10］。由于极端的质子-中子比，这些原子核具有较低的核子发射阈，是典型的开放量子系统特征。它们的最外层价核子弱束缚在核芯的周围，因此原子核中的多体关联和连续谱耦合等显得至关重要［11］。这些机制和奇特现象挑战着现有的原子核理论，将检验和加深我们对原子核的认识。

壳模型（Shell Model，SM）是研究原子核的主要理论方法之一，通过构建组态空间有效相互作用，能够合理地描述原子核能谱结构、衰变等性质［12］。随着手征有效场论［13］、自由空间相似重整化群［14-15］和量子多体方法［16-20］的发展，从第一性原理方法出发构建的有效相互作用已经适用于中重质量区开壳核计算［21-23］。同时手征三体力［24］的加入，使得第一性原理计算能更好地解释实验并精确地重现原子核性质，例如，氧同位素的滴线位置［25］，钙同位素链的壳演化［26-27］，电弱性质［28］以及镜像核中的同位旋对称性破缺［29］。迄今为止，第一性原理计算主要集中在闭壳核及其附近的原子核，通常使用谐振子基处理。对于深束缚原子核，谐振子基为多体计算提供了便捷，在合适的空间截断下能够很好地重现原子核特性。但是对于滴线附近原子核，它们属于开放的量子体系，谐振子基带来天然的截断，不能很好地描述原子核的近阈性质，例如共振态这种属于开放量子系统的内禀特征［11］。对于弱束缚和非束缚原子核，需要合适地处理共振态和连续谱效应，来描述这些开放量子系统中的奇特现象。

Gamow 壳模型（Gamow Shell Model，GSM）能够合适地处理和考虑共振和连续谱的影响［11］。与传统壳模型相比，它采用了同时包含束缚态、共振态和散射连续态的Berggren 系综［30］。但是，采用Berggren 系综会给理论框架带来一系列的困难［31］，例如，希尔伯特空间中无法描述具有指数衰减或者增长特性的态矢量。但Gamow 壳模型通过遵循Rigged 希尔伯特空间的量子力学形式，不仅能够严格地表述原有的狄拉克表示，而且还可以包含共振态等新概念，成功地把量子力学扩展到可以去描述衰变这种时间不对称过程。最终，Gamow壳模型能够提供多体框架下的束缚态、共振态和散射态间相互作用的统一描述。而第一性原理的Gamow 壳模型，则是从手征有效场论构建的两体和三体力出发，基于Berggren基矢，通过多体方法，同时考虑系统性改善的输入量、连续态耦合和多体关联等构建复对称的模型空间哈密顿量［21-22，29，32］。

本文将首先介绍第一性原理Gamow 壳模型的理论框架，再回顾该方法在氧同位素及其镜像核，碳同位素中的应用。

1 第一性原理Gamow壳模型

原子核物理中的第一性原理方法旨在从核物理最基本的自由度及其间相互作用出发，对原子核性质进行微观解释。它不依赖于经验参数，避免了模型中不可控的近似，因此，计算结果具有很好的普适性，是揭示和预测原子核性质的重要理论手段。核物理第一性原理计算的重大挑战源自于核力的复杂性和处理原子核多体系统的困难。

20 世纪30 年代，Yukawa［13］提出了介子交换理论，核力得到了长足的发展。目前，通过拟合核子-核子散射相移构建的现实核力被广泛地应用于核物理研究中，例如基于单介子交换模型的高精度Argonne V18势［33］、CD-Bonn 势［34］以及基于手征有效场论的核力N3LO［35］。其中，手征核力继承了量子色动力学（Quantum Chromodynamics，QCD）的手征对称性及其自发破缺，建立了与最基本理论间的桥梁。并且在手征有效场论框架下，多体力自然地出现。由于核子具有内部成分，多体力的存在是核子非基本粒子这一事实的自然结果。多体力特别是三体力在最近的第一性原理核结构和核物质计算中展现出至关重要的作用。虽然现实核力很好地描述了核子-核子间的散射相移，但由于它的短程排斥特性，在多体计算中会引起强烈的短程关联，通常采用Vlowk［36］或者相似重整化群［14-15］等重整化方法对核力进行软化，再进行多体计算。

原子核作为一个量子多体系统，以核子作为基本自由度，则A个核子构成的体系的哈密顿量可以写为：

式中：Ti是核子的动能项是两体核力是三体核力。求解上述哈密顿量的一种方法是在一组完备的多体基矢下直接展开体系的多体波函数，再对角化得到本征能量。由于谐振子基具有良好的解析性质，通常多体基矢由谐振子基的Slater 行列式构成。但由于计算能力限制，需要引入基矢的截断，这即是无核芯壳模型（No-core Shell Model，NCSM）［17］。随着核子数量A增加，这个过程的计算代价越来越大，因此，发展出了耦合簇方法（Coupled Cluster，CC）［19］、介质中相似重整化群（Inmedium Similarity Renormalization Group，IMSRG）［20］和多体微扰理论（Many-body Perturbation Theory，MBPT）［16，18］等一系列近似的但计算结果可系统改进的多体方法，将第一性原理计算的前沿推广到中重质量区域的原子核，并为奇特核和开壳核的研究开辟了新方向。

多体方法通常基于谐振子基展开，这为多体计算提供了便捷，但由于谐振子波函数的深束缚特性，它不能够有效地描述与外界环境有强烈耦合的开放量子体系原子核的近阈特性和远程渐进行为。Berggren基矢则是一种选择，它同时包含束缚态、共振态和散射连续态。

1.1 Berggren基矢

一般有两种方法获取Berggren 基矢：一种是在坐标空间选择辅助单粒子势场来产生共振和散射连续态。Woods-Saxon 势为有限深势阱，具有产生共振态所需的离心位垒，且通过设置合理的半径可以描述好原子核的密度分布，因此，它接近于真实的平均势场。故而通常选取Woods-Saxon中心场外加自旋轨道势和库仑势作为辅助场V（r），则径向单体薛定谔方程可以表示为：

其中：单粒子波函数u（k，r）即为包含束缚态、共振态和散射连续态的Berggren基矢。上述方程的两个线性无关解为库仑函数，且满足如下边界条件：

另一种方法则是在复动量空间自洽地求解Gamow Hartree-Fock 方程［22，29］。由于谐振子基的束缚特性，算符的远程行为会被谐振子基截断。但是对于远程具有平面波特性的粒子态，动能部分在远程处起主导作用，不能够被谐振子基截断，因此，我们可以选择在动量空间获取共振和散射态。首先根据基矢空间中Hartree-Fock方程：

其中：i，j表示对核芯所有粒子求和；tpq是动能项；和分别是用来提供正规化后单体势的两体和三体矩阵元，可以迭代得到单体Hartree-Fock 势U，得益于核力的短程特性以及费米面下填充的均为束缚态，谐振子基下迭代得到的单体势U直接转化到动量空间是合理的。为了能够描述共振态和散射连续态，通常利用谐振子波函数在动量空间的解析性，把单体势U解析延拓到复动量空间：

其中：〈k|α 〉是复动量空间的谐振子波函数；l，j分别是相应分波的轨道角动量和角动量。再通过离散化复动量空间Gamow Hartree-Fock方程：

其中：μ=m/（1-1/A），最终进行对角化就可以获得Gamow Hartree-Fock基矢。

在Gamow 壳模型计算中，通常采用Woods-Saxon势来产生单粒子Berggren基，Woods-Saxon参数由拟合实验单粒子能确定，能够准确地描述实验单粒子能。然而，数值结果在一定程度上取决于参数化的细节，且在多壳层情况下，由于缺乏跨壳单粒子能的实验数据，这种拟合比较困难。同时为了避免参数依赖，我们采用Gamow Hartree-Fock 方法生成Berggren基。这样Gamow壳模型更加自洽，因为基矢是由A核子哈密顿量本身提取出的单体势场产生的，而不是参数化的Woods-Saxon势。

1.2 复空间的多体微扰论

到目前为止，基于Berggren 基已经发展了无核芯Gamow 壳模型（No-core Gamow Shell Model，NCGSM）［37］、复空间CC［26］和Gamow IMSRG［38］等多体方法，但受限于Berggren 基的非简并性以及使用Berggren 基带来的计算量显著增长问题，这些方法只能计算闭壳及其附近原子核。而第一性原理Gamow 壳模型则是基于MBPT 框架在复空间构建模型空间相互作用，实现开壳原子核的计算。作为微扰方法，MBPT中核芯是自然分离的，不需要显式计算核芯部分，而且具有相对较小的计算量，因此适合于含连续谱的计算。并且在采用Hartree-Fock 基后，同样具有良好的逐阶收敛性。

进行复空间多体计算之前，首先需要把谐振子基下的两体、三体等矩阵元转换到Berggren 基［31］。然后以Berggren基下的单体和两体部分作为复空间MBPT 的初值，构建模型空间哈密顿量。为了简单起见，通常定义一个包含所有价连接不可约Goldstone图的顶点函数-box［16，18，21］，它对应着核子的各类激发模式和核子碰撞过程。模型空间哈密顿量最终可由ε）及其k阶导数表示：

其中：ω来自于相似变换哈密顿量H；ε0是起始能量；P表示模型空间的投影算符，对应其补空间的投影算符为Q。-box 的计算一般以两体部分作为小量作微扰展开处理，通常计算至两阶得到模型空间相互作用，而与其对应的单体部分-box［39-40］通常计算至三阶。最终可以得到模型空间哈密顿量：

其中：εpq代表计算-box得到的单体项，而“eff”表示由-box重整到价空间的壳模型有效相互作用。相比于基于Gamow Hartree-Fock 基的Gamow 壳模型的单体项采用-box 计算至三阶的结果，基于Woods-Saxon 基的Gamow 壳模型的单体项通常选取辅助场给出的单粒子能。上述的复对称模型空间哈密顿量最终可以通过m-scheme 的Jacobi-Davidson方法［41］实现对角化。

2 结果和讨论

本节回顾了弱束缚和非束缚核的第一性原理Gamow壳模型计算结果，主要集中在氧同位素及其镜像核［29］和碳同位素［42］。

2.1 氧同位素及其镜像对称性破缺

位于轻和中质量区交界处的Z=8氧同位素链由于其质子幻数特征，是检验理论方法的理想场所。同时随着趋近滴线，氧同位素展示出很多奇特现象吸引着实验和理论的兴趣。此外，N=8 同中子素和Z=8同位素中部分原子核能谱间展现了显著的镜像不对称现象［43］。因此，从手征两体力和三体力出发，基于Gamow Hartree-Fock 基矢，采用多体微扰理论构建sdpf7/2模型空间哈密顿量，研究了16O 的丰中子同位素17-28O 及其镜像对称同中子素17F-24S，并讨论了其能谱中的同位旋对称性破缺现象［29］。

图1 展示了以16O 为核芯计算的17-28O 的结合能和单中子分离能。为了提取三体力和连续谱耦合的贡献，我们分别基于两体力和两体力与三体力进行了基于实空间Hartree-Fock基的SM计算，以及基于两体力与三体力进行了GSM计算。计算显示，三体力的加入使得SM计算结果显著改进，此外，考虑连续态耦合的GSM 计算进一步改善了对结合能的描述，正确地重现了25O和26O的单中子分离能［44］，并且预测了28O不具备单中子发射特性，但允许双中子和四中子发射，其相对于24O的结合能为823 keV，共振宽度为357 keV。

图1 计算的氧同位素17-28O结合能和单中子分离能Sn与实验数据以及其他理论计算结果对比[29]Fig.1 Calculated 17-28O ground-state energies with respect to 16O and one-neutron separation energies Sn and their comparison with experimental data and other calculations[29]

此外，计算了17F-24S的结合能和单质子分离能，如图2 所示。与氧同位素链中计算结果类似，三体力显著地改善了SM 计算中结合能的过束缚现象。同时，由于库仑位垒的存在，17F-24S 基态中连续谱效应较弱。从19Na 开始，奇质子N=8 同中子素变不束缚，在含三体力的SM 和GSM 计算中均正确地再现，并正确地给出了20Mg 的Borromean 结构，而且GSM计算预测了22Si为N=8同中子素的质子滴线。

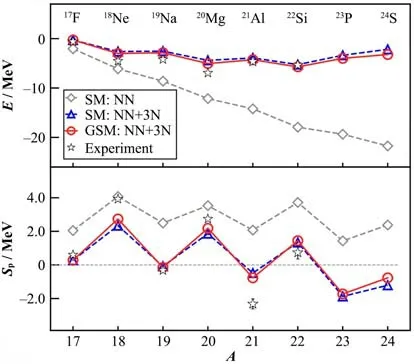
图2 计算的氧同中子素17F-24S的结合能和单质子分离能Sp，并与实验数据对比[29]Fig.2 Calculated 17F-24S ground-state energies with respect to 16O and one-proton separation energies Sp and their comparison with experimental data[29]

虽然丰质子N=8同中子素中存在库仑位垒对波函数的限制，但在激发谱中仍会出现强烈的连续谱耦合效应，如19Na 的1/2+态。实验观测到A=19 原子核的1/2+态具有显著的TES现象［43］。为了深入理解其中镜像不对称的起因，首先我们排除库仑力计算了19Na的激发谱，也即pp和nn相互作用的区别仅来自手征核力N3LO 中的CSB 和CIB［35］，从图3 看到，计算的19Na 和19O 间激发能谱对称性保持较好。当包含库仑力后，19Na中5/2+和3/2+态激发能几乎保持不变，而1/2+态显著降低。计算给出19Na的1/2+态几乎由一个纯的0d5/221s1/2

图3 19Na和19O的激发能谱中的TES现象[29]Fig.3 TES between low-lying spectra of 19Na and 19O[29]

1组态构成。由于s分波不存在离心位垒，所以相比于其他轨道1s1/2轨道的波函数在空间上更加延展，因此导致了占据1s1/2轨道的1/2+态中库仑能的贡献相对于其他激发态较小，最终导致能谱位置下降。含三体力的GSM 计算中19Na 中1/2+态由于连续谱耦合进一步下降，并且计算给出1/2+态是共振态，其共振宽度为0.28 MeV，这与实验给出的1/2+态共振宽度0.1 MeV 相当吻合［43］。

计算表明，三体力能够显著改善SM 计算对实验结果的描述。然而，要再现19Na 中1/2+的共振态特性和TES 现象，严格处理单粒子波函数的渐近行为及其与连续谱的耦合起着至关重要的作用。

22Si是一个非常有趣的原子核，文中进一步计算了22O和22Si的低激发能谱。图中给出了基于手征两体力与三体力的GSM计算结果，GSM计算的22O的激发能谱很好地符合了实验。对于其镜像核22Si，目前还没有实验数据，GSM 计算预测22Si 是丰质子滴线核，而且它的低激发态都是共振态。GSM计算的组态表明基态的6 个价核子主要占据在π0d5/2轨道上，而低激发态中有一个或者两个核子不同程度地激发到π1s1/2轨道上。由于π1s1/2单粒子轨道是共振态并且其轨道角动量l=0，故包含π1s1/2轨道成分的多体波函数在空间上更加地延展，这导致了图4中22Si的激发态中显著的TES现象。

图4 计算22O和22Si的激发能谱并与实验比较[29]Fig.4 GSM calculations of spectra for the mirror nuclei 22O and 22Si and comparisons with the experimental data[29]

2.2 碳同位素

作为sd壳层的另一个实验和理论研究热点，碳同位素中也存在着丰富的有趣现象。但是，对丰中子碳同位素激发谱的描述，特别是奇核子碳同位素的激发谱，一直是一个理论难题。因此，我们以14C为核芯，采用Woods-Saxon 基，选取现实核力CDBonn 势，用GSM 研究了碳同位素激发谱中连续谱耦合的影响［42］。

由图5看到，基于谐振子基的SM计算给出基态为5/2+，而实验得到的基态为1/2+［45-47］。通过计算19C相对于18C+n的谱因子，发现1/2+以s波为主，而5/2+以d波为主。具有零离心势垒（l=0）的s波与连续态有强烈的耦合，这显著降低了1/2+的能量，使得GSM计算给出正确的基态1/2+。

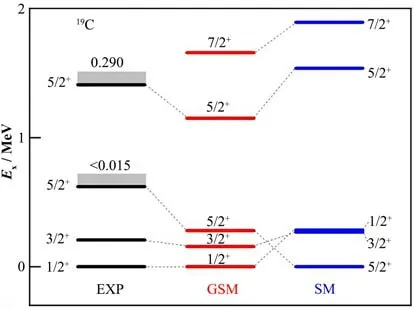
图5 GSM和SM计算19C的能谱，并与实验比较[42]Fig.5 Experimental and calculated levels of 19C based on the GSM and real-energy SM[42]

由实验可知，21C 是一个微弱的非束缚核，并且认为它的基态是1/2+［48］。如图6所示，考虑连续态耦合的GSM 计算重现了基态1/2+，而不考虑连续态效应的SM给出基态为5/2+。1/2+态由s波主导，并与连续谱间存在强烈的耦合，这导致了1/2+和5/2+之间顺序的反转。然而，GSM 计算给出的基态1/2+和激发态5/2+是弱束缚的，单中子分离能分别为Sn=0.96 MeV和0.83 MeV。而计算的3/2+、和7/2+等激发态为共振态。

图6 GSM和SM计算21C的能谱，并与实验比较[42]Fig.6 Experimental and calculated levels of 21C based on the GSM and real-energy SM[42]

图7展示了碳同位素的结合能。考虑连续态耦合的GSM 计算较合理地描述了结合能，并给出22C为中子滴线。然而，与实验相比，计算的22C、23C、24C过于束缚，大约相差4 MeV。在使用手征核力的计算中［32］，发现三体力对N=16 氧同位素滴线24O 及滴线外同位素的结合能具有显著的排斥效应。在N=16 的碳同位素22C 及更重的碳同位素中可以预期存在三体力的排斥效应，三体力的加入可能改善22C及更重碳同位素的结合能。图7还展示了基于手征两体核力N3LOW 的实空间壳模型（Realisticinteraction Shell Model，RSM）［49］和使用手征两体力与三体力的实空间的价空间介质中相似重整化群（Valence-space In-medium Similarity Renormalization Group，VS-IMSRG）［23］的计算结果。RSM 计算只给出了偶数碳同位素的基态能量。同时也展示了将单粒子能移动-427 keV后RSM的计算结果［49］。

图7 实验和计算的相对于14C的结合能，并与其他方法计算结果的比较[42]Fig.7 Experimental and calculated ground-state energies with respect to 14C and comparison with other calculations[42]