航空发动机加力燃烧燃油控制系统主动容错控制

杭杰，李运华，杨丽曼

北京航空航天大学 自动化科学与电气工程学院，北京 100191

对于高性能战斗机，航空发动机加力燃烧燃油控制系统的性能尤为重要。在加力燃烧燃油控制系统中，燃油计量装置负责军机加力工况的燃油流量的自动调节与供给，通过增加燃油流量二次燃烧获得推力提升。与主燃烧燃油控制系统不同，加力燃烧燃油控制系统工作条件更为苛刻，电液伺服阀、执行器及传感器等关键部件更容易发生故障，故急需设计容错控制策略（Fault Tolerant Control， FTC）以降低对系统控制性能的影响［1］。

阀控式燃油计量装置本质为电液伺服控制系统，其主要故障类型有传感器故障和执行器故障［2］。传感器种类多样，故障不尽相同，但都直接影响燃油系统控制精度，故应采取有效控制策略对其进行故障检测和识别（Fault Detection and Identification， FDI），以免酿成严重后果［3］。设计观测器以监测传感器故障是处理上述问题的有力措施之一［4］，如自适应观测器、扩展卡尔曼观测器和模糊观测器等。值得注意的是，未知输入状态观测器（Unknow Input Observer， UIO）因可有效解耦干扰和故障，现已被成功应用于诸多工业控制领域。Abu Nahian 等［5］利用少量历史数据设计UIO 以估计电液执行器中各类传感器故障，同时设计容错控制以提高系统鲁棒性。Tian 等［6］针对一类非线性离散控制系统设计非线性未知输入状态观测器（Nonlinear Unknown Input Observer， NUIO），以同时估计系统状态和传感器故障。Gao 等［7］针对具有非匹配扰动和传感器故障的燃气轮机，设计基于NUIO 的容错控制策略以提高系统控制性能。在以上文献中，UIO/NUIO 虽可有效处理传感器故障，但无法同时处理传感器故障、内泄漏故障和非匹配扰动。此为本文核心处理问题之一。

除传感器故障外，影响燃油系统控制性能的另一主要因素为执行器故障。执行器故障在航空发动机故障中占比约为25%，覆盖卡滞、断裂、磨损、泄漏和气蚀等失效形式。在上述故障中，由泄漏故障引起的质量问题占比近33%。与易监测的外泄漏不同，由加工/装配误差、磨损或工件变形引起的内泄漏故障率高且不易发现。内泄漏故障不仅会降低系统回路增益和控制精度［8］，亦会降低系统效率、平稳性和使用寿命。本文在文献［9］的基础上，为确保加力燃油计量装置在高供油压力大流量工况下的可靠运行，重点研究高性能容错控制以降低非匹配扰动、传感器故障和执行器故障对加力燃烧燃油系统控制性能的影响。

基于定量反馈理论的被动容错控制因需预先获悉故障类型，容错控制设计保守，现已逐渐被主动容错控制取代［10］。近年来，诸多研究将执行器故障定位为失效故障或不确定非线性扰动［11］。Wu［12］和Yao［13］等基于参数自适应律估计内泄漏故障，采用自适应控制策略恢复系统控制性能。此外，小波变换、Hilbert-Huang 变换和神经网络等技术为处理内泄漏故障提供新途径［14］。但上述文献并未考虑传感器故障或测量噪声对系统控制性能的影响。实际上，传感器测量的系统信号不可避免会引入测量噪声，进而引起系统抖动、性能下降甚至失效［15］。期望补偿技术不仅可节省在线时间，亦可降低测量噪声影响。但现有技术无法实现系统在外部扰动和测量噪声的工况下渐近跟踪［16］。此为本文第2 个核心处理问题。

综上所述，在非匹配扰动、传感器故障及内泄漏故障模式下，加力燃烧燃油控制系统难以实现高精度跟踪，而现有控制策略仅能处理一个或部分因素。为处理上述问题，本文提出一种基于NUIO 的自适应积分鲁棒控制策略。在非匹配扰动和多故障模式下，NUIO 可有效估计系统状态和传感器故障，且不受内泄漏故障和非匹配扰动影响。当传感器故障程度超过阈值时，由位移估计值取代实际测量值参与主动容错控制策略设计中。结合积分鲁棒控制和期望补偿自适应控制技术以同时处理传感器测量噪声、非匹配扰动下的内泄漏故障；通过引入误差辅助函数使误差符号积分鲁棒控制可直接处理非匹配扰动。

本文核心创新点如下：

1） 在非匹配扰动、传感器故障和内泄漏故障模式下，基于NUIO 的自适应积分鲁棒控制策略可有效实现燃油系统阀芯位移渐近跟踪。

2） 基于自适应参数估计的NUIO 可有效估计系统状态和传感器故障，且不受内泄漏故障和非匹配扰动影响。

3） 所提出的新型容错控制策略可在多种故障模式下权衡系统高效性、可靠性和经济性。

1 系统建模与问题描述

1.1 系统建模

燃油计量装置工作原理如图1 所示，其采用电液位置伺服控制计量活门开口与压差组件维持活门进出口压差恒定的流量控制原理［9］。该装置由离心燃油泵、电液伺服阀、计量活门、等压差组件和线性位移传感器等部件组成。其中，等压差组件由先导定差减压活门、主级执行活门、阻尼活塞、动态阻尼及其余附件组成［17］。高压涡轮通过齿轮箱驱动增压泵和高压离心泵，燃油泵出口处的部分燃油经定值减压阀流向伺服阀以控制计量活门开度，另一部分燃油经计量活门通向加力燃烧室，为发动机提供热能以获得二次推力提升。具体地讲，伺服阀输出控制油进入活门控制腔，通过控制活门阀芯轴向位移调节计量窗口通流面积A，先导压差活门可维持计量活门进出口压差ΔP恒定，大部分计量后燃油经主级执行活门流向加力燃烧室。当计量活门阀芯按指定规律运行时，即可实现出口流量Q按规律计量：

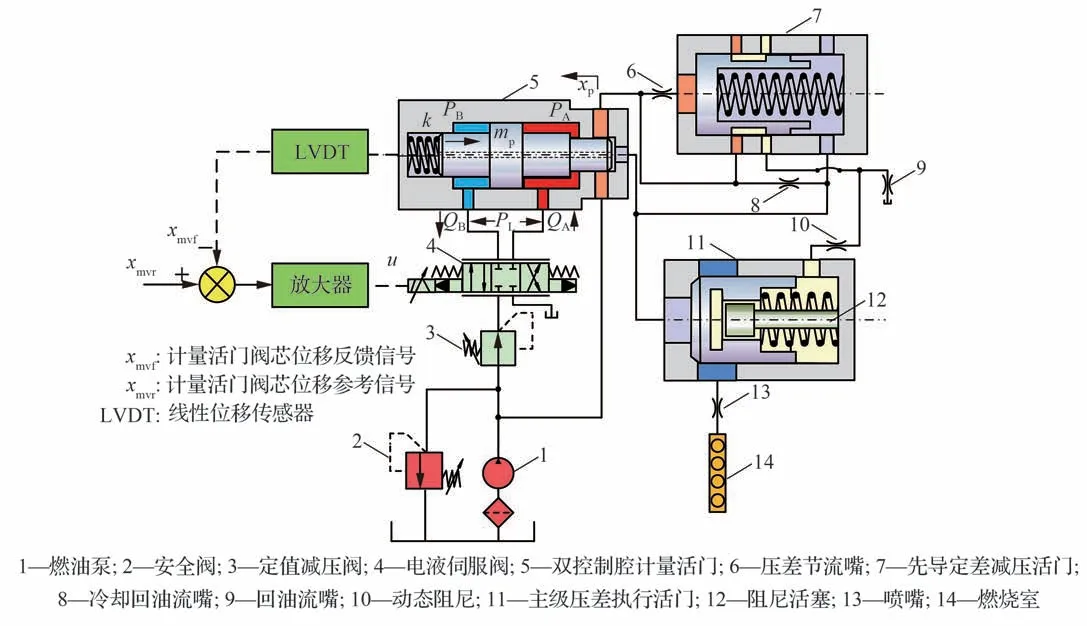
图1 航空发动机燃油计量装置工作原理图Fig.1 Working principle architecture of fuel metering unit in aeroengine

式中：Cd为流量系数；A为计量活门通流面积；ρ为燃油密度；ΔP为计量活门进出口压差。

计量活门受力平衡方程为

式中：mp为计量活门阀芯及负载折算到阀芯的总质量；xp为阀芯位移；PL=PA-PB为负载压力，其中，PA和PB分别为计量活门两端控制腔内压力；Fs=2CdCvWpcosαΔPxp为阀芯所受稳态液动力；f(xp，ẋp，t)为未建模不确定性，如外干扰和阀动态等；Ffe(xp，ẋp，t)为非线性摩擦力的集总，包括已知摩擦力Ff(xp，ẋp，t)和未知外部摩擦力Fe(xp，ẋp，t)，其中，Ff(xp，ẋp，t)=Fv(ẋp)+Fm(ẋp)，Fv=fvẋp为黏性摩擦力；fv为黏性摩擦系数；Fm(ẋp)=Fmp1tanh(Fmc1ẋp)+Fmp2[tanh(Fmc2ẋp) -tanh(Fmc3ẋp)]为具有Stricbeck 效应的静态摩擦力，Fmc1、Fmc2和Fmc3为摩擦特性形状系数，Fmp1和Fmp2为不同摩擦特性幅值水平，函数tanhx满足

计量活门两腔压力动态特性方程可表示为

式中：βeA=βeB=βe为燃油体积弹性模量；VA=VA0+Apxp，VB=VB0-Apxp分别为计量活门进出口腔的容积，其中VA0和VB0分别为两腔初始容积；qL(t)为计量活门内泄漏流量；QA和QB分别为计量活门两控制腔燃油流量，其表达式为［18］

式中：kq为伺服阀流量增益；xs为伺服阀阀芯位移。

为使非线性函数S（x）光滑可微，定义S(x) ≜2 πarctan(1 000x)代替符号函数signx；忽略伺服阀动态特性，令xs=kiu，ki为电流增益。

当计量活门发生内泄漏时（即活门密封存在缺陷），基于Thompson 理论［13］，内泄漏流动可视为湍流孔口流动，故式（4）中qL(t)可表示为

式中：Ct0为活门名义内泄漏系数，m5(N·s )；Ct为内泄漏故障发生时泄漏系数分别表征系统发生严重内泄漏、早期内泄漏和轻微内泄漏时的泄漏系数；η(t-Tf)表征为从时间Tf开始时活门发生内泄漏故障，其表达式为

式中：μ＞0 表示活门内泄漏发生速率；μ=0.5表示内泄漏故障缓慢发生；μ=5 表示内泄漏故障平稳发生；μ=10 时，η(t-Tf)近似阶跃信号，表示内泄漏故障突发。

当线性位移传感器发生故障时，计量活门阀芯位移反馈信号xp由xp+xf代替。假设线性位移传感器故障xf由未知输出信号ζ引起［19］，即

定义变量x=[x1，x2，x3，x4]Τ≜[xp，ẋp，PL，xf]Τ，由式（2）～式（8）可得燃油系统动态方程：

结合工程实际，燃油系统动态方程（9）具有高强度非线性及模型不确定性等特性：

1） 电液伺服阀压力流量非线性。由于非线性函数S(x)及开方函数的作用，控制输入具有非线性特性，故燃油系统属于不连续非仿射系统。

2） 微分方程结构非线性。当计量活门阀芯位移较大或阀活门间连接油路体积较大时，活门两腔控制容积VA=VA0+Apxp和VB=VB0-Apxp以分母形式进入系统，直接影响燃油系统非线性压力的动态特性、跟踪精度和谐振频宽。

3） 活门摩擦非线性。当系统高速运行时，可将摩擦简单视为纯黏性摩擦；但系统低速运行时，非线性摩擦对其控制性能影响较大，如Coulomb 摩擦、Stribeck 摩擦及Dahl 效应。故在控制器设计过程中应考虑非线性摩擦效应。

4） 模型不确定性。燃油系统模型不确定性主要包括受工况影响的黏性/库伦摩擦和弹性模量等参数不确定性和外干扰、未建模泄漏/摩擦和阀动态等不确定非线性。

5） 高标准性。在加力状态下，战斗机推力提升50%，军用航空发动机所需燃油流量增至2 倍。高供油压力大流量的作业工况对加力燃烧燃油控制系统的可靠运行提出严峻挑战。

综上所述，燃油控制系统的高强度非线性、模型不确定性、不确定非线性和苛刻的作业环境是限制航空发动机加力燃烧系统控制精度的核心所在。本文所设计的基于NUIO 的鲁棒积分自适应容错控制器如图2 所示。

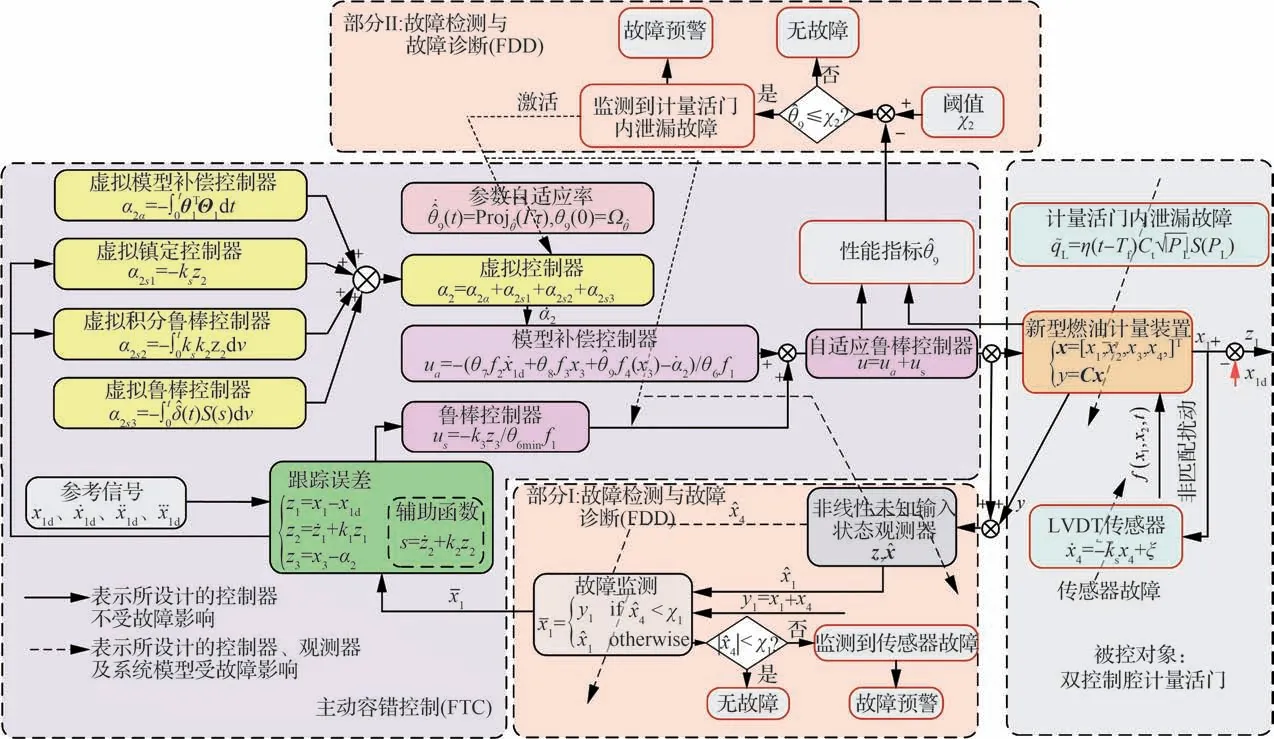
图2 主动容错控制结构Fig.2 Structure of active fault tolerant control

1.2 问题描述

本文研究目标为当燃油控制系统存在传感器故障、内泄漏故障和非匹配扰动时，设计主动容错控制器，使x1在有限时间内跟踪到期望轨迹x1d。在此前，做如下假设：

假设1除线性位移传感器存在故障外，燃油系统内部其余信号真实可测且有界。

假设2参考位移指令yd=x1d∈C3有界。

假设3活门两端控制腔内压力有界，即

假设4燃油控制系统内的内泄漏故障和非匹配扰动有界，即

式中：θmin和θmax分别为不确定参数上下确界；δ为系统非匹配扰动的上确界。

说明1本文仅考虑内泄漏故障对计量装置控制性能的影响，故由内泄漏决定的参数θ9未知，其余参数可以离线识别，且参数识别误差可视作非线性不确定项，故系统满足持续激励（Persistent Excitation， PE）条件。

说明2由假设2 和假设3 可知，f1(x1(t))不为0。为便于控制器设计，令非匹配扰动d(t)是一阶可微的。非匹配扰动足够光滑假设是合理的，因在实际系统中不存在产生不连续力/力矩的物理执行器。假设4 合理性已被试验验证［13，20］。

2 基于NUIO 的主动容错控制器设计

2.1 参数自适应律

定义未知参数θ9的估计值为θ̂9，定义非连续映射函数：

定义参数自适应律：

式中：为参数自适应增益；为待定自适应函数。定义误差

引理1参数自适应函数τ满足如下性质：

非连续映射函数使得参数始终在给定范围内变动。引理1 证明过程详见文献［18］。

2.2 非线性未知输入状态观测器设计

航空发动机加力燃烧燃油控制系统中存在的诸多干扰无疑增大了FDI 设计难度。传统基于模型的故障诊断方法需使用含有未知输入信号残差，故障检测与识别的精确度较低。本文设计基于参数自适应律的NUIO，可有效解耦干扰和故障，以避免系统残差。

令x(t)=[x1(t)，x2(t)，x3(t)，x4(t)]Τ，改写燃油控制系统状态方程（9）：

式中：d1(t)=[d(x1，x2，t)θ1，ξ]；B=[0，0，θ6，0]Τ；A=[0，1，0，0；θ2θ1，θ3θ1，1θ1，0；0，0，0，0；0，0，0，-ks]；E=[0，0；1，0；0，0；0，1]Τ；C=[1，0，0，1；0，1，0，0；0，0，1，0]；g0(x(t))=[0，0，f4(x3(t))，0]Τ；g1(x(t))=[0；θ4θ1Fm1(x2(t))+θ5θ1Fm2(x2(t))；θ7f2(x1(t)，x2(t))+θ8[f3(x1(t)，x3(t))]；0]。

假设g(x)和g0(x)是非线性函数，且满足Lipschitz 条件，即

式中：γ＞0 和γ0＞0 为常数。

使用估计值代替真实值θ9，设计NUIO：

定义NUIO 误差为

现确定矩阵F、T、K、H，分为以下3 步：

步骤1为使(HC-I)Ed1(t)=0，矩阵H应满足

由于rank(CE)=rank(E)，式（21）解得

步骤2为消除非线性项g0(x(t))和输入u(t)，故取

步骤3令

由于系统((I-HC)A，C)可检测，选取K1，以使F=(I-HC)A+K1C指数稳定；取K2=FH

则式（20）可改写为

说明3在后续控制器设计中，NUIO 估计值x̂1和传感器测量真实值y1的切换，由阈值χ1［5］决定，输出值xˉ1参与后续主动容错控制器设计中。

在分析 NUIO 稳定性前，现说明若=0，则式（25）指数稳定，证明如下：

定理1假设=0 且|θ9|≤M(M＞0)。假设存在对称正定矩阵P，使得

式中：ι＞0 为常数，则式（25）指数稳定。

证明见附录A。由定理1 可知，本节NUIO的设计思路是：利用未知参数估计器(t)代替真实值θ9，使得参数误差→0(t→∞)，最终实现式（25）渐近收敛到0。

2.3 自适应鲁棒积分容错控制器设计

针对燃油控制系统动态方程（9），将积分鲁棒控制和期望补偿自适应控制相结合，设计新型容错控制器。

步骤1设计虚拟控制。定义跟踪误差：

求导可得ż1=x2-ẋ1d。定义状态x2虚拟控制：

定义跟踪误差：

式中：α2为x3的虚拟控制；k2为正反馈系数；s为辅助滤波函数以增加控制系统的设计自由度。

对式（31）中第2 式两端同乘θ1并求导可得

故可设计虚拟控制α2为

式中：为自调节增益，满足=r|s|；

其中：τs为采样时间，辅助函数h(t)满足

说明4 引入式（36）可避免使用加速度信号，以降低传感器噪声对系统控制性能的影响。

将式（33）代入式（32），则有

将式（9）代入式（37）中，可得：

式 中 ：f2d=f2(x1d，ẋ1d)；f3d=f3(x1d，x3)；ξ3=θ7f2(x1，x2)-θ7f2(x1d，x2)，ξ4=θ8f3(x1，x3)-θ8f3(x1d，x3)。

步骤2设计鲁棒自适应控制器u

式中：k3为正反馈系数。由式（39）可知，鲁棒自适应控制器u包含2 部分，分别为前馈模型补偿项ua和线性鲁棒控制项us。

在控制器（38）下，s满足

式中：Θ2=f4(x3)。

在控制器（38）下，z3满足

2.4 主要结论

定理2燃油控制系统动态方程（9）中同时非匹配扰动、传感器故障和内泄漏故障，采用基于NUIO（18）和参数自适应律（B7）的主动容错控制（38），并选取合适增益k1、k2、k3和ks，使矩阵Λ正定：

证明见附录B。

3 仿真验证

3.1 仿真设置

本文基于Vxworks 开发的Jetlab 平台实时仿真系统［9］，验证所提出控制器的有效性，详见图3。其中，主机用于模型设计和仿真管理；目标机用于实现实时仿真；RapidForm 软件用于仿真管理，包括状态监视、仿真工程管理、代码下载和操作管理等。采样时间为1 ms。给定加力燃烧燃油控制系统足够光滑可微的类正弦信号x1d=0.01arctan[sin( πt)][1-e-t] 0.078 4。设置非匹配扰动为f(t)=50arctan[sin(0.8πt)(1-e-t)]；系统主要结构参数见表1，各控制器参数如下：

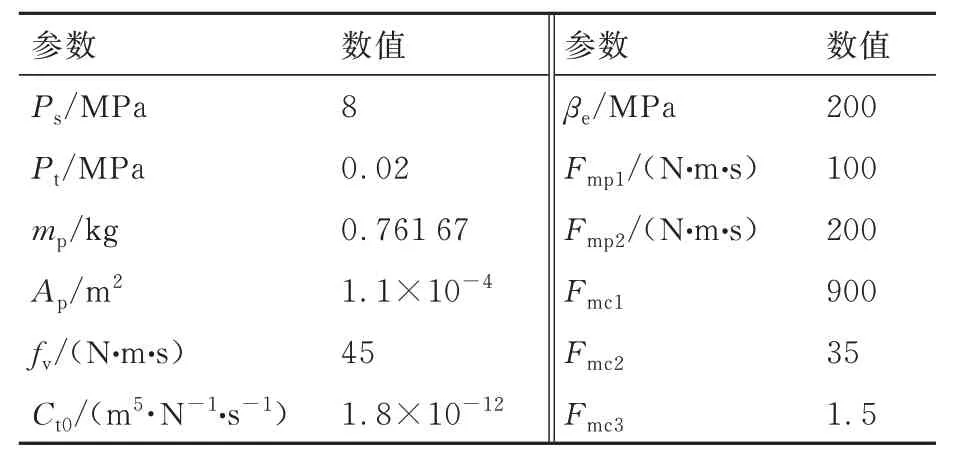
表1 燃油计量装置主要结构参数Table 1 Main structural parameters of fuel metering unit

图3 基于JetLab 的实时仿真测试平台Fig.3 Real time simulation test platform based on JetLab

1） AIRFTC （Adaptive Integral Robust Fault Tolerant Control） based on NUIO，本文所提出的基于NUIO 的自适应积分鲁棒容错控制。系统未知参数初始值为θ0=4.0×10-9，参数自适应增益Γ=1×10-12。容错控制器反馈增益为k1=200，k2=9 500，k3=2 000；ks=4 500，r=0.5。UINO设置如下：H=[0，0，0；0，1，0；0，0，0；1，0，0]；T=[1，0，0，0；0，0，0，0；0，0，1，0；-1，0，0，0]；K=[0，1，0；0，0，0；0，1，0；0，-1，0]；F=[-5，0，-10，-5；-5，-10，0，-5；10，10，-10，-10；-5，0，0，-5]。

2） ARFTC （Adaptive Robust Fault Tolerant Control） based on UNIO，即 AIRFTC不含α2s3。

3） AFTC （Adaptive Fault Tolerant Control） based on UNIO，即基于NUIO 的传统的自适应容错控制。由式（9）计算控制律u和自适应函数τ：

4） VFPI（Velocity Feedforward Proportional Integral） control based on UNIO，即基于NUIO 的速度前馈PI 控制器：

式中：kp=5 000；kI=50；kF=30。

说明5通过AIRFTC、ARFTC 和AFTC与VFPI 对比，验证非线性控制器的高效性与优越性；通过AIRFTC、ARFTC 与AFTC 对比，验证AIRFTC 和ARFTC 处理传感器测量噪声和内泄漏故障的优越性；通过AIRFTC 与ARFTC对比，验证AIRFTC 处理非匹配扰动的有效性。

本文采用最大跟踪误差Me、平均跟踪误差μe、跟踪误差的标准值σe、ITAE 和ITSE［20］评价各个主动容错控制器的性能：

1） 用于评价跟踪精度的Me可表示为

式中：N为所记录误差数字信号的数量。

2） 用于评价平均跟踪性能的μe可表示为

3） 用于评价跟踪误差偏差水平的σe可表示为

4） 用于评价误差收敛速度的ITAE 可表示为

5） 用于评价瞬态响应后期出现误差偏离水平的ITSE 可表示为

3.2 传感器故障

当系统于t=10 s 时，线性位移传感器发生故障。设置线性传感器故障参数如下：ksf=0.5，ζ=0.01+0.005sin(πt)，阈值为χ1=0.003。

本方案主要分析NUIO 对传感器故障处理的性能，主控制器仍采用AIRFTC。由图4（a）可知，NUIO 可有效估计系统状态和故障，且不受内泄漏故障和非匹配扰动影响。如图4（b）所示，系统于t=10.28 s 时，传感器故障估计值x̂4≥χ1，故障标志Im1报警。特别地，如图4（a）和图4（c）所示，当传感器故障时，即传感器反馈信号y1偏离期望轨迹x1d，NUIO 介入，使位移估计值x̂1取代实际测量值y1参与AIRFTC 设计，即=x̂1。

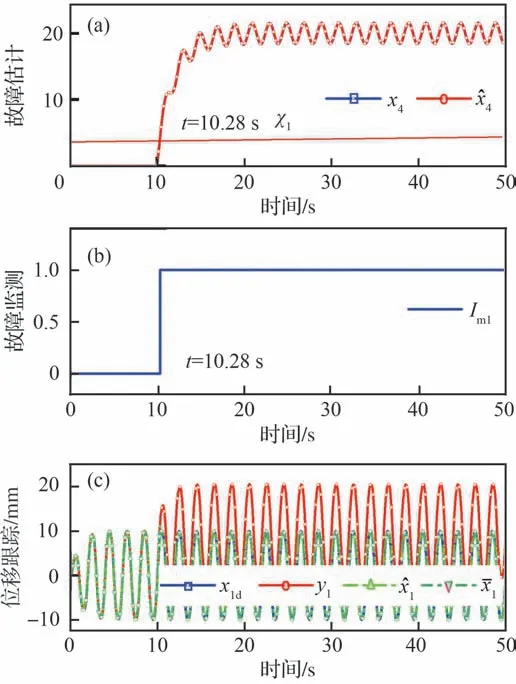
图4 传感器故障下的状态监测与位移跟踪Fig.4 Status monitoring and tracking under sensor failure

在图5 中，y1NUIO、e1NUIO和uNUIO分别代表基于NUIO 的AIRFTC 的位移反馈、跟踪误差和输入电压。当x̂4≥χ1时，激活NUIO，由x̂1代替y1，使y1NUIO精确跟踪x1d，降低跟踪误差；特别地，如图5（c）所示，引入NUIO 并未增大输入能量（u=uNUIO）。故可知该技术在提高控制精度的同时不增加控制成本。2 种方案性能指标见表2。

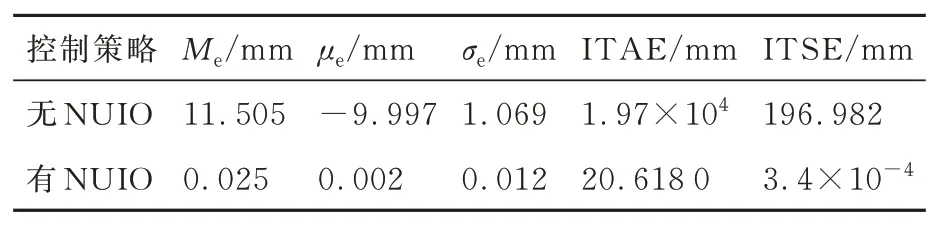
表2 传感器故障模式下最后2 个周期的性能指标Table 2 Performance indicators for last two cycles under sensor failure

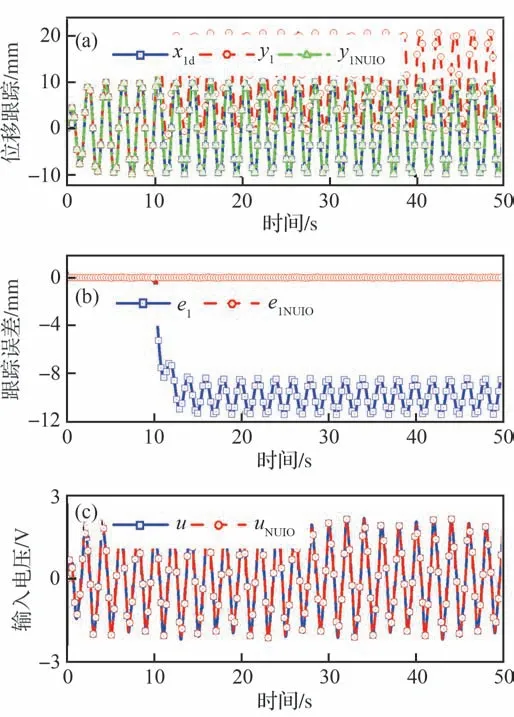
图5 传感器故障下NUIO 性能分析Fig.5 NUIO performance analysis under sensor failure

说明6传统燃油计量装置常采用双冗余传感器以提高系统可靠性。本节所提出的NUIO不仅可有效检测传感器故障状态，确保系统在传感器故障模式下正常运行，亦可减少传感器数量，降低维护成本。在完善航空发动机健康管理的同时，亦提高燃油计量装置的经济性。

3.3 内泄漏故障

提高燃油泵出口压力虽可有效增大出口流量进而提高战斗机推重比和作战性能，但在大流量大压降的工况下，内泄漏故障则易使系统超负荷作业，进而造成无法估计的后果。本节所提出的AIRFTC 结构简单，易于在实际系统中实现，可有效提高系统容错性和经济性。其主要特点如下：当系统无故障时，系统可满足所规定的性能指标；当系统发生轻微泄漏时，故障无需报警，由正常鲁棒控制器覆盖该故障，并使系统满足所规定的性能指标；当系统发生严重内泄漏和早期内泄漏时，故障报警，激活容错控制器，以补偿内泄漏对系统的影响，从而恢复系统控制性能。

本文所提出的AIRFTC 可视内泄漏为系统参数变化，只需改变正常鲁棒控制器中的参数，故其结构简单且易于实现。学习过程基于在线监测的PE 条件进行操作，可确保参数自适应的良好收敛性。FTC 控制器激活后，系统性能逐渐恢复。

1） 严重内泄漏故障。结合图6 和图7，当t=30 s 时，内泄漏故障θ̂9≥χ2，故障标志Im2报警，AIRFTC 激活，进行扰动补偿。图7（a）显示输入能量u增大，控制性能经2 s 后恢复。由图7（b）可知，AFTC 和VFPI 在初始内泄漏下，控制性能不佳，当发生严重内泄漏故障时，性能衰退尤为显著。图7（c）显示，与ARFTC 相比，AIRFTC在严重内泄漏故障发生时，系统超调较低，调节时间缩短，即表明：α2s3可有效处理非匹配扰动，无需增设观测器。表3 证明上述结果的准确性。

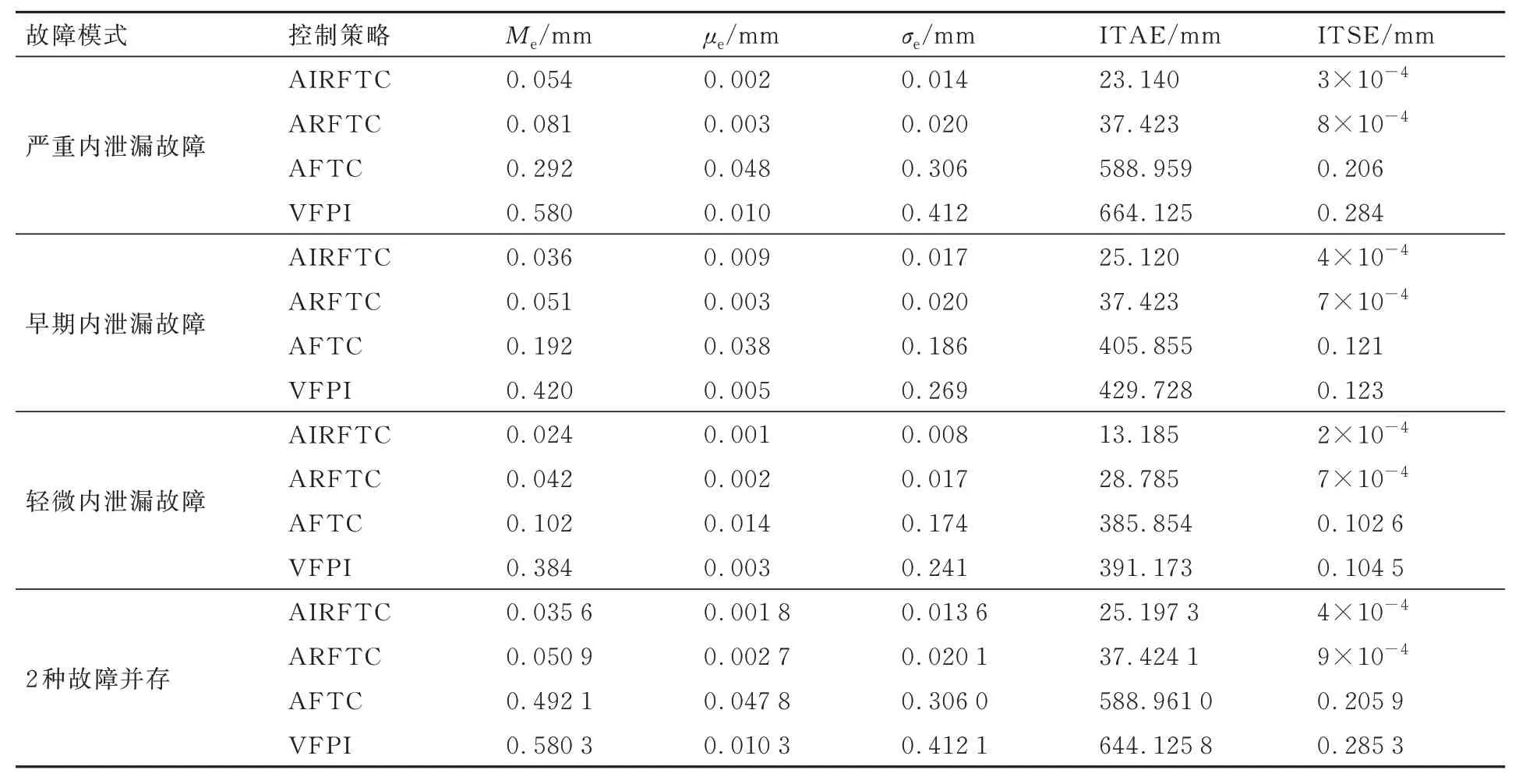
表3 最后2 个周期的性能指标Table 3 Performance indicators over last two cycles

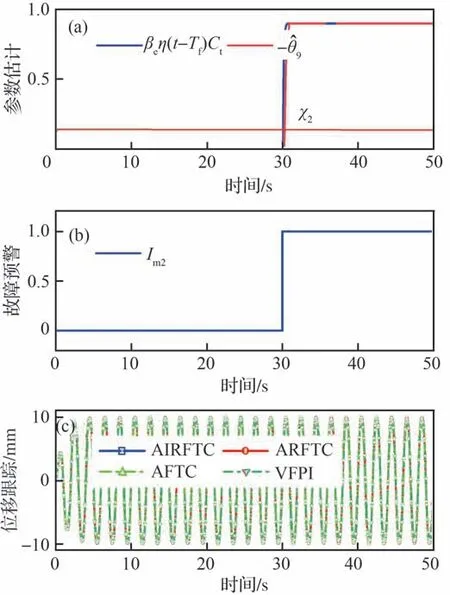
图6 严重内泄漏下故障监测Fig.6 Fault monitoring under severe internal leakage

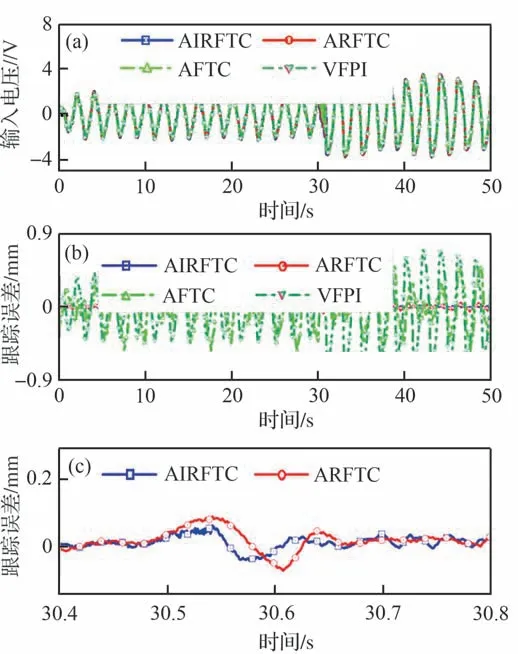
图7 严重内泄漏下输入电压与跟踪误差Fig.7 Voltage and tracking error under severe internal leakage

2） 早期内泄漏故障。如图8 和图9 所示，系统于t=30 s，系统发生缓慢内泄漏故障。此时＜χ2，内泄漏故障对控制性能影响较小，未触发故障标志Im2，AIRFTC 将此视为扰动进行补偿处理，并使系统满足所规定的性能指标。当t=32.8 s 时≥χ2，故障标志Im2报警，AIRFTC 激活。由图9（b）可知，AFTC 和VFPI 在初始内泄漏下，控制性能不佳，当发生早期内泄漏故障时，性能衰退亦为显著。图9（c）显示与ARFTC 相比，AIRFTC 可获得更好的跟踪性能，即表明：α2s3可有效处理非匹配扰动，无需增设干扰观测器。对比图7（c）可知，AIRFTC 在处理早期内泄漏故障时，控制性能提升尤为显著。表3 亦可有效证明上述结果的准确性。

图8 早期内泄漏下故障监测Fig.8 Fault monitoring under early internal leakage

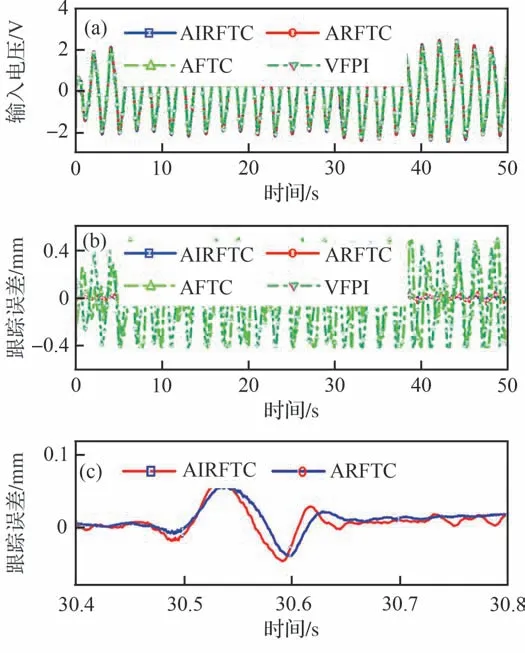
图9 早期内泄漏下输入电压与跟踪误差Fig.9 Voltage and tracking error under early internal leakage

3） 轻微内泄漏故障。由图10（a）和图10（b）可知，此时内泄漏故障流量小于允许内泄漏最大值，即内泄漏故障程度小于阈值＜χ2。此时系统未触发故障标志Im2，所设计的正常鲁棒控制器AIRFTC 将该故障视为模型不确定性进行扰动补偿，故覆盖该故障，并使系统满足所规定的性能指标。如图11（a）所示，因未激活参数自适应，故4 种控制器输入电压在轻微内泄漏故障发生前后维持不变，即输入能力不变。由图11（b）可知，AFTC 和VFPI 在初始内泄漏下，控制性能不佳，当发生轻微内泄漏故障时，性能表现依旧不佳。如图11（c）所示，与ARFTC 相比，AIRFTC 在轻微内泄漏故障发生时，非线性鲁棒项α2s3可有效处理系统中存在的较大非匹配扰动，加力燃烧燃油控制系统在超调量和调节时间等性能指标方面均获得较好地改善。表3 可证明上述结果的准确性。

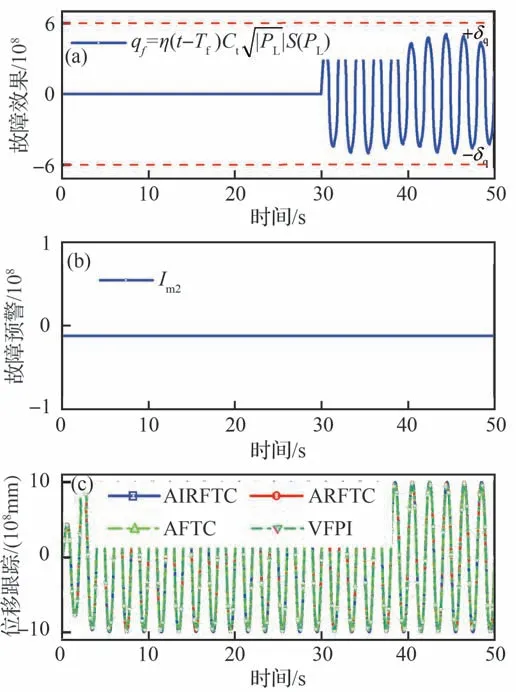
图10 轻微内泄漏下故障监测Fig.10 Fault monitoring under slight internal leakage

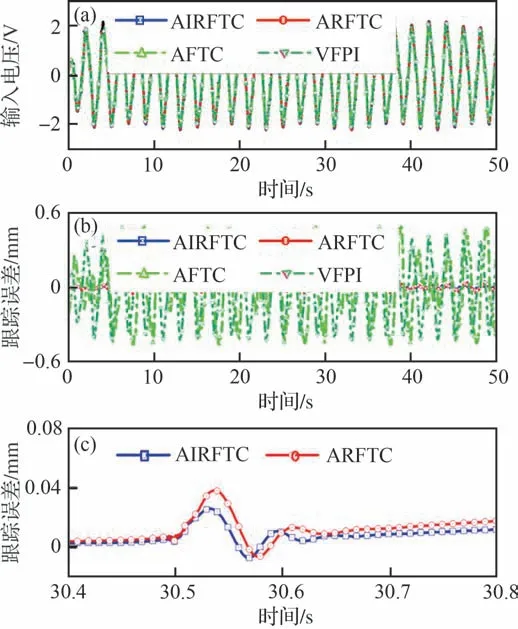
图11 轻微内泄漏下输入电压与跟踪误差Fig.11 Voltage and tracking error under slight internal leakage

综上所述，轻微故障容限的概念可能会在加力燃烧燃油控制系统性能和经济性间做出权衡。

3.4 2 种故障并存

本节主要分析在非匹配扰动、传感器故障和内泄漏故障并存的模式下，验证基于NUIO 的AIRFTC 策略的优越性。

由图12（a）和图12（b）可知，所设计的AIRFTC 可有效估计传感器故障x̂4和严重内泄漏故障θ̂9。由图13（a）可知，t=10 s 时激活NUIO并未增加系统输入电压，t=30 s 时激活参数自适应律，AIRFTC 输入电压较其余3 种控制器较大，消耗能量较多。由图13（b）可知，与其余3 种控制器相比，当传感器故障发生时，AIRFTC 可有效减短调节时间。当严重内泄漏故障发生时，AIRFTC 在超调量、调节时间和稳态误差方面均有较好的表现。表3 可证明上述结果的准确性。

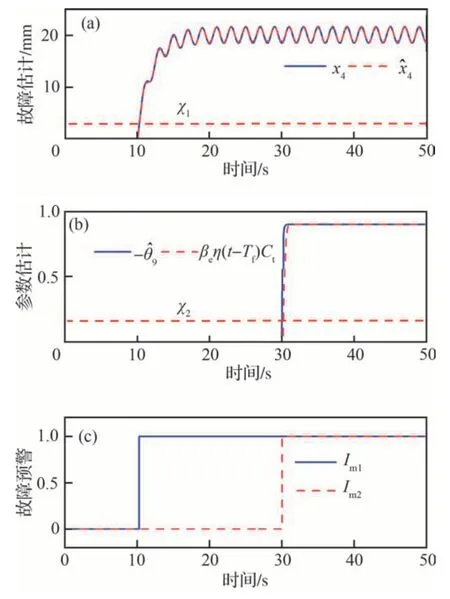
图13 2 种故障并存下性能分析Fig.13 Performance analysis under whole faults

4 结 论

针对航空发动机加力燃油控制系统，提出了一种能同时处理非匹配扰动、传感器故障和执行器故障的新型主动容错控制策略，主要结论有：

1） 非线性未知输入状态观测器NUIO 可以估计位移信号和传感器故障，且不受内泄漏故障和非匹配扰动影响。

2） 通过滤波跟踪误差构造辅助函数，提出了基于积分鲁棒控制和直接自适应控制的自适应积分鲁棒容错控制策略AIRFTC。仿真结果表明，在非匹配扰动、传感器故障、内泄漏故障并存模式下，所提出的主动容错控制在Me、μe、σe、ITAE 和ITSE 等性能上均有改善，分别降至0.035 6、0.001 8、0.013 6、25.197 3、4×10-4mm，即验证AIRFTC 的有效性和高效性和经济性。

3） 采用Lyapunov 理论，证明了基于NUIO的AIRFTC 策略可确保加力燃烧控制系统在多种故障模式下的渐近跟踪性能。但AIRFTC 控制器在同时处理2 项及以上执行器故障时，目前尚不能证明NUIO 的稳定性和系统是否满足PE条件，因此不能证明参数自适应的收敛性。后续作者将围绕这个问题开展进一步的研究。

附录A：

定理1 证明：定义式（25）的Lyapunov 函数为

对E(t)求导，可得

附录B：

引理2ξi(i=1，2，3，4)满足如下性质：

式中：ηi＞0，i=1，2，3，4 为常数。

证明：根据中值定理，存在δ1∈(ẋ1d，x2)，使得

引理3虚拟控制α2s3具有以下性质：

定理2 证明： 定义Lyapunov 函数为

对V(t)求导，并将式（30）～式（32）、式（39）、式（41）和式（A2）代入得

式中：ϑ9和ϑ10由式（41）给定。

当传感器发生故障时，即。显然设F=(F)ij，由式（25）得

为消除内泄漏对系统稳定性的影响，设计参数自适应函数：

由Young 不等式可得

则式（B5）可改写为

由式（B9）可知，V∈L∞，系统变量z、s和x͂有界，从而系统状态x和状态估计x̂有界，进而所设计的容错控制律u有界。同时该式显示所提出的容错控制器具有渐近稳定的收敛性能，即随着t→∞，W→0，即z1→0。