自适应湍流耦合建表燃烧模型的振荡燃烧数值模拟
2023-08-31陈涛徐兴平张宏达韩省思
陈涛,徐兴平,张宏达,韩省思,*
1.南京航空航天大学 能源与动力学院,南京 210016
2.中国航发沈阳发动机研究所,沈阳 110015
由于环境保护法规的逐渐严格,现代燃气轮机及航空发动机等动力设备的燃烧室设计越来越多采用预混、部分预混的贫燃燃烧方式[1]。但是,贫燃预混燃烧的燃烧不稳定性某些情况下较差,易于激发热声耦合振荡燃烧模态,导致振荡燃烧问题。振荡燃烧具有很强的破坏性,甚至可能伴随有回火、固体形变等多种问题[2]。对于振荡燃烧物理机理的研究已经成为国际热点和难点问题之一。
针对复杂燃烧系统的振荡燃烧试验技术复杂,存在成本较高、数据不完备等不足。随着数值模拟技术的快速发展,其逐渐成为燃气轮机及航空发动机等燃烧设计研发的重要辅助工具之一。对于非稳定燃烧,特别是热声耦合振荡燃烧问题的高精度、高效数值预测显得尤为重要。程林[3]采用雷诺应力和涡耗散模型,对轴向旋流器外加激励条件下的振荡燃烧特性开展了多参数的数值研究,表明振荡幅值对热声耦合具有重要作用,频率的逐渐增大对释热脉动作用并不显著。Han 等[4-5]采用燃烧和声波二者解耦的方法,基于低马赫数大涡模拟,以火焰描述函数耦合低阶声学网络模型的方式,数值预测了剑桥大学钝体驻定燃烧室的极限环振荡模态,计算结果与试验测量吻合较好。Laera 等[6]通过有限元方法构建了有热源的非线性火焰模型,通过亥姆霍兹求解器对纵向模态,及环形燃烧室分别进行了极限环参数数值研究,计算结果良好,且可用于复杂外形的工业燃烧器。Shahi 等[7-8]在通用可压缩求解器上分别测试了SAS(Scale-Adaptive Simulation)湍流模型和涡耗散、PDF(Probability Density Function)建表和BVM(Burning Velocity Model)模型等多种燃烧模型耦合对LIMOUSINE 自激振荡的数值预测效果,其中BVM 燃烧模型对振荡燃烧的频率预测精度较好。该方法对于长火焰的单一纵向模态燃烧室具有较好的应用前景。Chen 等[9]采用大涡模拟和修正的FGM(Flamelet Generated Manifolds)燃烧模型对旋流燃烧室自激工况进行了数值计算,振荡火焰形态和试验比较接近,但预测的振荡频率低于试验值。Fredrich等[10]将Pant 等[11]构建的一种新的可压缩LES(Large Eddy Simulation)-PDF 数值计算方法应用于经典的PRECCINSTA 单旋流燃烧室,并成功捕获了完全自激的极限环振荡燃烧模态,预测的热声耦合振荡特征频率和试验数据吻合良好。Xia 等[12]则在CFD 和有限元波动方程耦合的方法 中 ,采 用 URANS(Unsteady Reynolds-Averaged Navier-Stokes)湍流模型探究了LIMOUSINE 燃烧室自激振荡的临界工况模态,成功预测了特征声学主频,但振荡幅值的预测相比试验值偏高较多。
前期研究中发现,振荡燃烧中振荡幅值的数值预测结果受到多种因素的显著影响,如湍流模型、湍流燃烧模型、数值耗散、壁面边界、出口边界等。通常情况下准确预测振荡幅值难度较大。除了上述湍流模型和燃烧模型的影响外,文献中对其他影响因素也做了深入的分析和讨论。高阶数值格式[13-14]可以更精确地捕捉燃烧室中火焰位置和反应区域,对于径向声学模态具有更好的预测,也就是对于高振荡频率的幅值预测具有更好的适用性。壁面边界[15-16]通常和声学边界[17-18]共同作用,主要反映为壁面的几何结构和传热特性对声学边界阻抗值和燃烧温度及组分壁面反应的影响。总之,对于振荡燃烧,频率的预测和多种耦合机制相关,但不论哪种振荡机制,压力脉动振幅的预测具有更大的难度。实际研究中,特别是试验研究中,通常需要精细地设计试验装置,以削弱或控制壁面边界、出口边界等因素对振荡燃烧的影响。针对本文研究的经典的LIMOUSINE 部分预混燃烧室振荡燃烧问题,前期数值研究结果中对数值差分格式、壁面边界、出口边界等因素的影响已经提供了一定的参考。但是对于如湍流模型和湍流燃烧模型的影响还有待深入研究。
高精度数值计算得益于更加完备的计算数据,对于振荡燃烧物理机理的探究具有较明显的优势。目前,高精度的自激振荡燃烧的数值预测较多采用大涡模拟,而大涡模拟对于复杂的燃烧室计算网格要求较高,从而导致计算量很大。基于此,发展高效率且具有高精度的计算方法尤为重要。
目前,振荡燃烧的数值计算可分为解耦方法和直接耦合方法两大类。解耦的振荡燃烧预测方法将非定常燃烧和声学求解进行解耦。非定常燃烧需要大量的CFD 参数计算以构建足够样本和可靠性的火焰描述函数。若采用大涡模拟进行计算,工作量较大,对于工业应用尚有不足。直接耦合计算方法是在可压缩求解器上,直接通过高精度的非定常计算获得振荡燃烧的结果,即在同一个计算框架内一次完成某个工况下的非定常燃烧和声学的耦合计算过程,对于工业应用具有较大的吸引力[19]。
基于此,本文拟进一步发展耦合的振荡燃烧数值模拟方法,以在保证计算精度的前提下进一步提升计算效率。在自适应超大涡模拟方法框架下,耦合可压缩的建表燃烧模型FGM 方法,评估不同的燃烧源项封闭方法。针对经典的LIMOUSINE 部分预混燃烧室开展自激热声耦合振荡燃烧数值研究,验证其对燃烧不稳定的预测精度,探究在部分预混燃烧下热声振荡的模态特性和内在机制。
1 数学物理模型
1.1 自适应湍流模型SATES
本文采用的自适应湍流模型(Self-Adaptive Turbulence Eddy Simulation,SATES)框架是由Han 和Krajnović[20-22]长期发展并广泛验证的VLES(Very-Large Eddy Simulation)模型方法。严格的理论推导表明,Han 和Krajnović[20-22]发展的VLES 方法在网格足够精细的情况下和LES完全等价,并且可以根据当地计算网格尺度、湍流未解的大尺度、最小的Kolmogorov 尺度三者之间的关系自动调节湍流模化求解的比例。由于湍流模化过程自适应调节,因此本文将该方法称为自适应湍流模拟方法SATES。
自适应湍流模型SATES 方法基于低马赫数牛顿流体假设求解Favre 过滤的控制方程,其中残余湍流应力τij的模化基于BSL(Baseline)k-ω模型进行求解。通过分辨率控制函数Fr对湍流黏性系数μt进行重新模化,使其达到网格分辨率相关的残余尺度。分辨率控制函数Fr是SATES方法的核心,具体形式为
式中:Lc、Li和Lk分别为截断网格长度尺度、积分长度尺度和Kolmogorov 长度尺度,3 个湍流尺度的表达式为
其中:Cx为重要的模型参数,是连接自适应湍流模型SATES 和传统的大涡模拟LES 之间的桥梁。在最初的SATES 模型中,通过引入LES 和RANS 模型常数进行模化,得到的模型常数为Cx=0.61[20]。
在本研究中,为进一步优化SATES 模型对于复杂物理过程的求解,在前期理论推导基础上[22],通过理论分析,得到了更加统一的模型参数模化形式,即采用依据流场参数动态确定模型参数:
式(5)即为本研究新发展的优化的SATES模型参数求解模型。可以看出,与原始模型中Cx=0.61 不同,新模型的参数随流场变化存在时空演化,从而可以更加准确地描述湍流的演化过程。
在BSLk-ω湍流模型的基础上,通过分辨率控制函数Fr模化后的湍流黏性系数表达式为
湍动能k和比耗散率ω的输运方程与经典的BSLk-ω模型完全一致,具体为
如式(1)所示,分辨率控制函数Fr的取值根据网格分辨率的不同在0~1.0 之间平滑取值,以此定量确定湍流的模化程度。当Fr→1 时,μt→,即SATES 将趋近于底层的非定常RANS 湍流模型;当Fr→0 时,μt→0,即SATES方法将趋近于直接数值模拟(DNS)方法。其余模型参数及变量定义可参考文献[22-24]。
1.2 FGM-FSD 燃烧模型
本文采用详细化学热力学建表的火焰面生成流型湍流燃烧模型(FGM)耦合火焰面密度方法(FSD)。FGM 假定湍流火焰的标量演化可以用层流火焰中的若干标量演化进行近似。通过求解简化的层流火焰方程,采用有限个特征标量描述化学反应过程,结合假定的PDF 模型描述湍流燃烧的相互作用。预先建立包含温度、组分等信息的化学热力学表,在考虑了详细化学反应机理的同时,减少了直接求解标量输运方程的个数,极大地降低了计算量。
但是FGM 燃烧模型将湍流和燃烧解耦之后,对于强烈的湍流燃烧相互作用过程的计算需要进行验证和考量。火焰面密度方法FSD 可以保证部分预混或者预混火焰中火焰传播速度的正确性,从而可以宏观上较好地处理湍流和燃烧的相互作用。但是通常火焰面密度模型FSD 模化形式较多,不同的FSD 模型形式对结果的影响较大。振荡燃烧属于强烈的非定常燃烧过程,因此对燃烧模型的可靠性要求更高。Lecocq等[25-26]成功将FGM 和FSD 这2 种方法耦合,并数值探究了PRECCINSTA 燃烧室的预混燃烧工况,取得了较好的效果。
针对火焰面密度模型FSD,Boger 等[27]提出了一种通用的火焰面密度形式:
其中:Ξ为褶皱因子,表征湍流脉动对火焰面的影响,是火焰面密度模型构建的核心参数之一。
本文分别采用Fureby[28]与Zimont 和Lipatnikov[29]提出的模型方法:
式中:模型的其他具体参数及定义可参考文献[27-30],这里不再赘述。
在FGM 燃烧模型中,湍流燃烧源项的封闭有多种形式,通常为有限速率方法和湍流火焰速度方法。有限速率方法封闭为
式中:P是反应进度变量和混合物分数的联合概率密度函数,有限速率采用积分形式封闭源项。
湍流火焰速度方法则具有和火焰面密度相似的定义,具体形式为
通过湍流火焰速度封闭的方法可以将建表燃烧模型FGM 和FSD 方法进行耦合。同时,相比有限速率方法,褶皱因子可以通过校准实现更加精确地预测火焰面位置。本研究中通过式(10)~式(12)对其进行封闭。
通常FGM 燃烧模型采用假定Beta 分布积分获得湍流化学热力学表,一般在非绝热状态下需要计算联合混合物分数、未归一化反应进度变量及其方差以及热焓即可。但对于不稳定的振荡燃烧直接计算,需要考虑声波的求解,因此需要采用可压缩的求解形式。而解耦方法中的密度、压力和温度将不会受到声学的影响,因此,本文采用考虑可压缩性的FGM 建表方法。可压缩的FGM 建表将修正后的流体密度和压力利用理想气体状态方程重新耦合求解,从而可以保证声学波动和燃烧过程二者之间的强烈耦合。
2 试验工况与数值设置
本研究将第1 节所述数值计算方法应用于经典的LIMOUSINE 燃烧室[31],并对其多个工况进行数值模拟研究。LIMOUSINE 燃烧室是荷兰特温特大学(University of Twente)为研究热声耦合振荡燃烧发展的部分预混燃烧室,本文采用V3 燃烧室版本,其基本结构如图1 所示。燃烧器上游和下游分别由2 个不同宽度的矩形管道组成,中间由一个正三角体分隔。上游矩形通道为25 mm×150 mm,轴向长275 mm,根据文献[7-8]的研究,当发生不稳定燃烧时,声学在钝体后流场对燃烧产生较大影响,但对于上游的影响通常较小。因此,本文计算中简化上游长度为80 mm;下游矩形通道为50 mm×150 mm,轴向长780 mm。正三角型钝体边长为22 mm。空气通过上游注入燃烧室内,纯甲烷燃料通过正三角体上的1 mm 孔注入后与空气快速掺混,并在钝体面后进行燃烧。本文计算中将甲烷喷孔整体简化为1 mm 宽的狭缝。
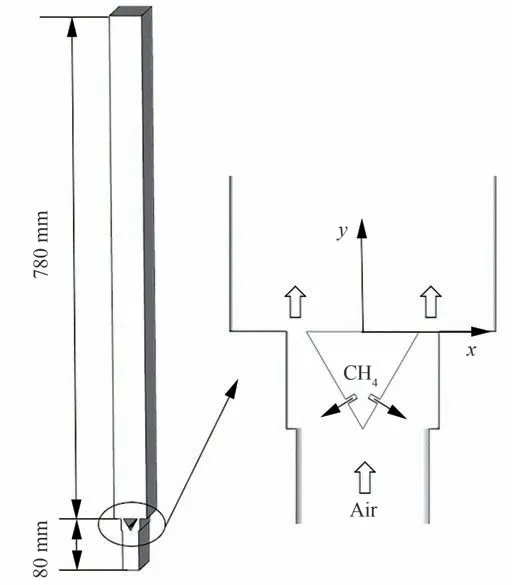
图1 LIMOUSINE 燃烧室几何结构Fig.1 Geometric diagram of LIMOUSINE combustion chamber
试验研究中探究了多种不同的振荡燃烧工况,燃烧功率包括20、40、50、60 kW,覆盖了完全发展的极限环振荡燃烧到稳定燃烧状态。不同燃烧功率下,燃料流量不同;相同燃烧功率下,空气流量不同,即空气系数λ不同(空气系数的定义同余气系数)。本文主要计算了3 个典型的振荡燃烧工况,具体参数见表1。

表1 数值计算工况Table 1 Working condition of numerical calculation
本文采用全结构化网格离散计算域,燃烧室内网格分布比较均匀。在甲烷和空气掺混的突扩结构处略有加密,燃烧室内最小网格尺寸为0.1 mm。考虑到本研究中保留了整体下游的结构,燃烧室长度较长,因此燃烧室网格沿轴向以1.15 的比例逐渐增大。依据自适应湍流模型SATES 方法的优势,本文经过多套计算网格测试后,最终网格总数约为280 万。正三角型钝体附近网格示意如图2 所示。同时,为了验证计算网格对计算结果的影响,本文将55 万、140 万、280 万网格分别标记为网格M1、M2、M3。
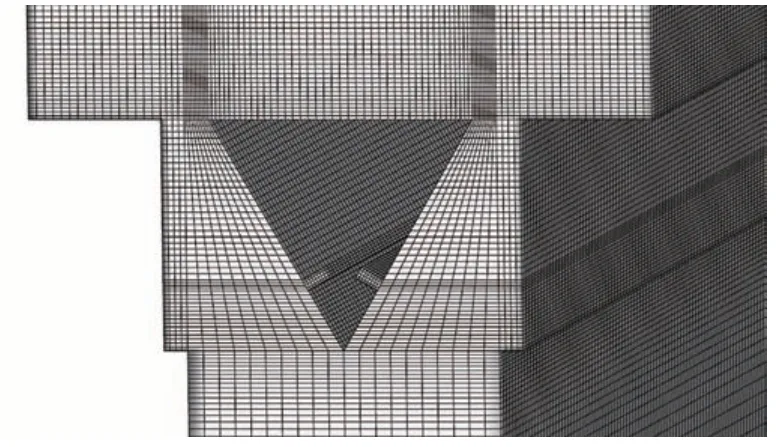
图2 计算域部分网格示意图Fig.2 Schematic diagram of partial grid of computational domain
极限环热声耦合振荡燃烧数值预测影响参数较多,声学边界是影响参数之一,对振荡幅值具有明显的影响[32]。本文研究中空气进口和甲烷进口均采用质流量进口边界,保证和试验中质流量一致。根据Rochette 等[31]的试验测量结果,出口边界在压力出口的基础上可以设为声学完全开放边界;其余固体壁面均为无滑移壁面边界条件。具体进口参数设置参见表2。
表2 数值计算进口边界条件Table 2 Inlet boundary conditions for numerical calculation
热声耦合振荡燃烧的重要信息隐含于压力脉动信号中,本文数值预测中采用和试验一样的多点监测方法,分别在上游y=-10 mm,下游y=200,500,650 mm 设置4 个压力监测点,相对位置如图3 所示。其中,PMT200 mm 的流向位置和试验研究中PMT4 的测点位置一致,也是振荡压力时序信号的核心测点位置。
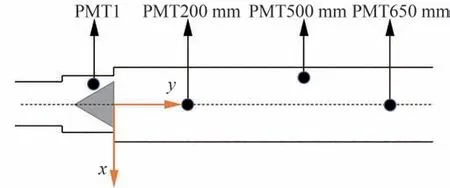
图3 压力监测点位置示意图Fig.3 Schematic diagram of pressure monitoring points
数值计算中为保证非定常计算具有较高的采样频率,设置非定常计算时间步长为8×10-5s。燃烧模型中详细化学反应建表采用GRI 3.0 详细化学反应机理。基于有限体积方法进行离散,时间项采用二阶中心隐式格式推进;动量通量采用有界二阶中心格式离散;标量通量采用二阶迎风格式离散。压力速度耦合算法采用SIMPLEC算法。
3 结果与讨论
3.1 不同湍流燃烧模型预测结果
本研究在振荡燃烧工况C1 上,对比研究了不同燃烧源项封闭方法下的燃烧模型对振荡燃烧特征主频和振幅的数值预测效果。分别将有限速率模型、Zimont 和Fureby 封闭的FSD 模型方法简记为W1、W2 和W3。
在工况C1 的试验测量结果中,燃烧室中声学振荡特征主频为234.06 Hz,压力振荡振幅为801.09 Pa。3 种不同的源项封闭模型计算的特征主频快速傅里叶变换(FFT)结果对比如图4 所示。可以看出,有限速率(W1)、Zimont(W2)和Fureby(W3)对振荡主频的预测结果比较,分别为227.22、249.28、236.59 Hz,和试验测量值236.06 Hz 的相比误差均较小。但是,3 种源项封闭方法预测的压力振荡幅值预测差异较大,有限速率(W1)、Zimont(W2)和Fureby(W3)预测的压力脉动振幅预测数值逐渐减小,分别为8 050.2、3 081.21、975.28 Pa,相比于试验测量值801.09 Pa,Fureby(W3)模型方法预测的压力脉动振幅最接近试验结果,误差约为17.9%,而其他2 个燃烧模型的结果误差>380%。
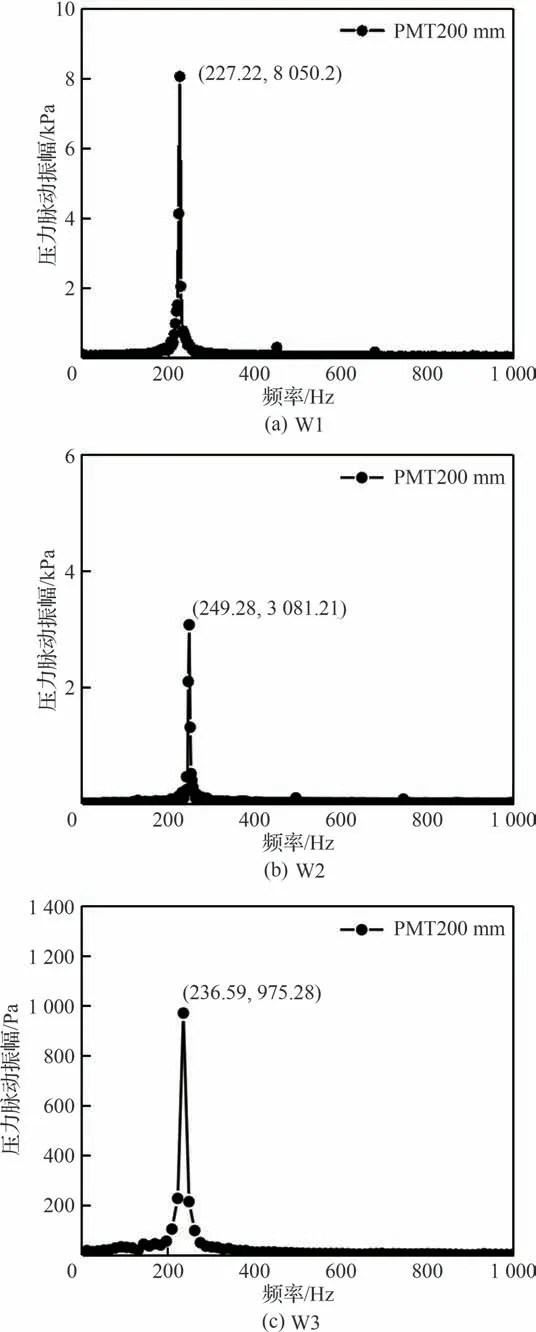
图4 3 种燃烧模型(W1、W2 和W3)预测的特征主频结果对比(工况C1)Fig.4 Comparison of results of characteristic principal frequency predicted by three combustion models(W1, W2 and W3) (Condition C1)
结合图5 中压力和体积热释放速率的信号时序图来看,3 种燃烧模型方法的体积热释放速率和压力变化趋势比较接近,即二者相位存在强耦合。此时,燃烧火焰和声波之间形成了正反馈回路,燃烧室处于振荡自激模态。但是,有限速率(W1)和Zimont(W2)模型的体积热释放的振荡幅值很大,是Fureby(W3)燃烧模型的若干倍。因此,在W1燃烧模型的数值预测过程中,呈现的燃烧振荡更加激烈,W2 次之,W3 最低也最接近试验值。同时发现在W1 和W2 的预测中,体积热释放率存在负值的情况,且随着预测振幅偏差的加剧,体积热释放速率的负值表现越强,也就是说,在数值计算中,若计算的振荡过于剧烈,超过了实际振荡幅值太多,会使计算出现局部熄火的特性。
图6 和图7 为3 种燃烧模型在同一时刻下的温度标量场和轴向速度场对比分布。云图分布同信号分析结果相一致。W1 燃烧模型在高强度的压力振幅下,回火严重,高温燃烧向贴着三角型钝体壁面两侧向甲烷燃料进口蔓延。W2 和W3 模型的振幅预测相对W1 模型较低,受声波振幅的往复影响,但未形成严重的回火现象,火焰高温燃气均向下游区域伸展的同时表现为强烈的褶皱结构。但W2 模型预测的火焰稳定比W3模型结果较差,这与W2 模型的振幅较强相关;类似地,W1 和W2 模型预测的火焰涡团卷吸相比W3 模型更加明显,体现在速度场的中心回流区变化很大。速度向下游发展中,W3 模型受声学影响主要体现在下游剪切层的不稳定,而W1 和W2 模型的湍流失稳均向上游狭缝靠近,特别是W1 模型,已经在三角型钝体的上游位置形成了新的回流区,这会对下游形成阻塞,进一步降低燃料和新鲜氧化剂的掺混效果,更加增强火焰的不稳定性。从试验结果来看,W3 模型预测结果更加接近于真实物理过程,但W1 模型和W2 模型的预测结果也体现了振荡加剧后的强烈非定常火焰演化。
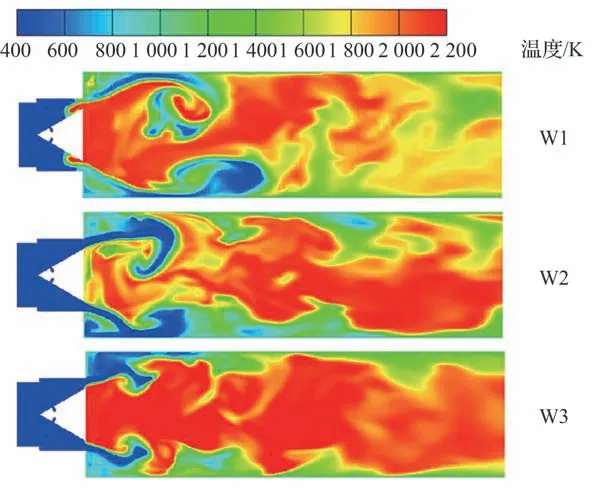
图6 同一时刻下W1、W2 和W3 模型预测的温度分布瞬时图对比结果(工况C1)Fig.6 Comparison results of temperature distribution instantaneous maps predicted by W1, W2 and W3 models at the same time (C1)
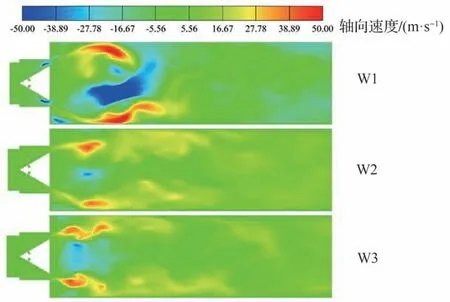
图7 同一时刻下W1、W2 和W3 模型预测的轴向速度分布瞬时图对比结果(工况C1)Fig.7 Comparison results of instantaneous maps of axial velocity distribution predicted by W1, W2 and W3 models at the same time(Condition C1)
3 种燃烧模型的不同预测结果表明,部分预混的不稳定振荡燃烧,特别是极限振荡环状态下,数值预测结果对湍流及湍流燃烧模型具有很强的敏感性。针对源项的封闭方法,直接体现在相同条件下,不同的源项方法预测的火焰燃烧速度差异较大,燃烧速度过快/过慢,声学某一模态可能和燃烧过程、高温已燃气体的发展相互耦合,热声正反馈回路的形成会逐渐增强,如有限速率(W1)和Zimont(W2)2 种源项模型的结果。但这与本文中LIMOUSINE 燃烧室的试验结果是不一致的。Fureby(W3)封闭源项燃烧模型正确预测了本文中的热声耦合振荡燃烧模式,即燃烧速度相对较慢,部分燃料在受声学振幅影响卷入卷出速度回流区,向下游发展的同时相对缓慢地燃烧完全,声学模态和燃烧过程剪切层相耦合,因此,Fureby(W3)模型预测的振荡特征幅值和频率均与试验结果比较相近。
进一步地在C1 振荡燃烧工况的W3-Fureby湍流燃烧模型上,分析了计算网格对计算结果的影响。计算网格M1、M2 和M3(分别包含55 万、140 万和280 万网格)的计算对比如图8 所示。网格M1 预测的结果为频率217.69 Hz,压力脉动振荡幅值为670.35 Pa;网格M2 预测的结果为频率211.86 Hz,压力脉动振荡幅值为582.37 Pa。粗糙网格M1 和M2 预测值比较接近,相比试验值均偏小。网格较为粗糙时,对振荡燃烧中强烈非定常性的涡系捕捉变弱,无法捕捉小尺度的涡系演化。因此压力脉动的振幅精度变差。得益于SATES-Fureby 湍流燃烧模型,粗糙网格M1、M2 的预测结果也比较合理,但M3 的预测精度更高,特别是振荡频率的预测。考虑到不同工况的涡系特征差异,以较细的M3 计算网格开展后续多工况的振荡燃烧计算具有更高的计算精度。
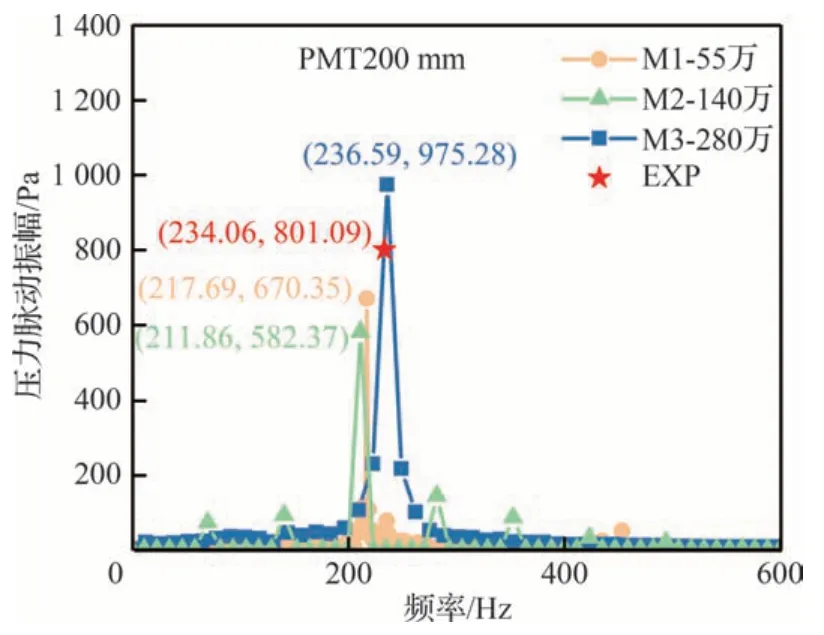
图8 不同网格在工况C1 下数值预测结果对比Fig.8 Comparison of numerical prediction results of different grids under Condition C1
3.2 不同工况数值结果
根据3 种不同燃烧模型源项封闭方法的计算结果对比,发现Fureby 模型在振荡燃烧特征主频和振荡幅值的预测上均优于其他2 种方法。因此,本文下述章节研究采用了Fureby 褶皱因子模型,对LIMOUSINE 燃烧室继续开展多工况的热声耦合振荡燃烧研究。根据试验结果,工况C1 和C3 为极限环振荡燃烧工况,C3 的振荡比C1 更加强烈,C2 为火焰稳定和不稳定的过渡状态[31]。
如表3 所示,给出了3 种不同工况下本文的数值计算和试验结果对比。3 种工况的特征主频预测值与试验吻合均较好,压力脉动振幅预测结果中工况C3 和C1 误差相对较大,工况C2 的误差较小,但最大误差不大于17.9%。特别地,也给出了针对工况C2 文献[12]中采用URANS-SST湍流模型结合有限速率封闭源项的FGM 方法预测的结果对比,如表4 所示(Xia 等[12])。可以看出,URANS 方法预测的工况C2 特征主频峰值约为300 Hz,振幅约为3 000 Pa,相比本文的数值结果,URANS 频率和振幅的预测精度误差均较大。可能的原因是本文采用了SATES 自适应湍流模型耦合更加精确的Fureby 燃烧模型,对湍流燃烧的脉动过程预测得更加准确,因此,对于非定常效应强的热声耦合不稳定燃烧,大涡方法相比URANS 方法精度更高。同样,本文也给出了工况C3 的大涡模拟结果[33],如表5 所示。Hernández 等[33]采用AVBP-Smagorinsky 对工况C3 的相近条件下的燃烧室作了热声耦合数值预测。相比于本文的工况C3,仅空气系数一项由1.2 增大至1.25。因此,文献[33]预测的振荡主频略高于试验值,本文预测结果和LES 相比,二者预测的差异在合理的范围之内,均与试验结果吻合比较好。
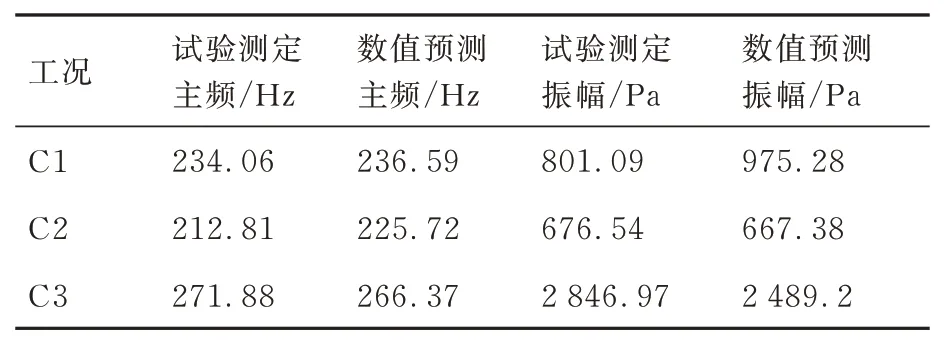
表3 多工况下本研究数值预测与试验结果[31]对比Table 3 Comparison of numerical prediction and test results[31] under multiple operating conditions

表4 工况C2 本研究数值预测与URANS[12]结果对比Table 4 Comparison of numerical prediction and URANS[12] results under Condition C2

表5 工况C3 本研究数值预测与LES[33]结果对比Table 5 Comparison of numerical prediction and LES[33] results under Condition C3
图9 为工况C2 中热释放速率和平均混合物分数的散点分布图。热释放速率随着混合物分数的变化呈现较宽的分布范围,在平均混合物分数0.045 附近较为集中,即火焰燃烧在相对广泛的掺混范围中发生,进一步证实本文发展的数值方法较好地预测了LIMOUSINE 燃烧室部分预混的特性,也侧面反映了流动掺混过程的准确预测对计算结果的显著影响。
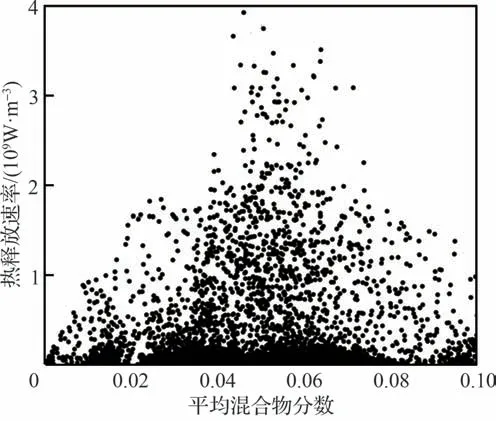
图9 工况C2中热释放速率随平均混合物分数的散点分布Fig.9 Scatter plot of heat release rate vs average mixture fraction under Condition C2
图10 为工况C2 中本文计算结果和文献[7]的时均流场结果对比,其中图10(a)为PIV 拍摄结果,图10(b)为文献[7]中SAS 湍流模型计算结果。可以看出,本文的数值方法可以有效地捕捉到振荡燃烧过渡状态工况C2 的基本流场结构,包括突扩后典型的中心回流区和侧回流区。但根据图10 中0 速度线分布可知,本文预测的中心回流区长度略短于试验结果[7]。
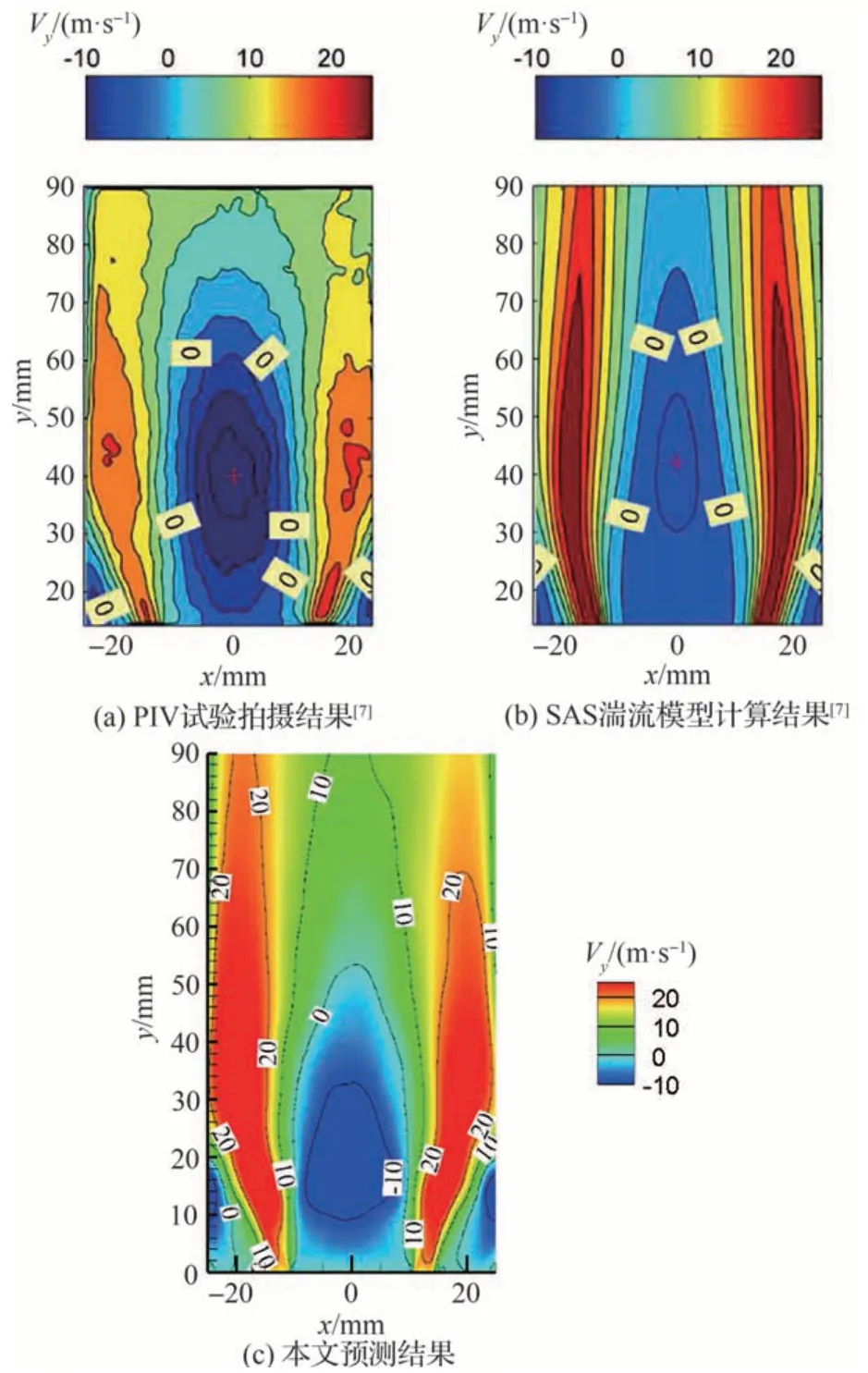
图10 工况C2 中平均流场分布对比结果Fig.10 Comparison results of average flow field distribution in Condition C2
图11 为工况C1 一个振荡周期内,燃料甲烷的分布示意图。该序列显示了火焰随着声学振荡特性的周期振荡特征。甲烷自喷嘴进入下游,起初的掺混过程较弱,随后甲烷经过突扩狭缝后在湍流回流区的作用下,自剪切层开始抖动,强化掺混后进行燃烧;与声学耦合的特性进一步增强了振荡的幅值。当正弦运动到负相位时,甲烷被阻塞在钝体狭缝中一段很小的距离,此时,振荡特性提前强化了燃料的掺混。当下一个相位来临时,甲烷流出顺畅,又重新在钝体回流区下游的剪切层位置掺混并燃烧,如此往复。同时,与非定场湍流的中心回流区相耦合,甲烷燃料在中心回流区附近一侧会卷吸进入中间位置,另一侧则向下游伸长延展,最终不稳定火焰在这样2 个往复过程中形成极限环模态的振荡燃烧。
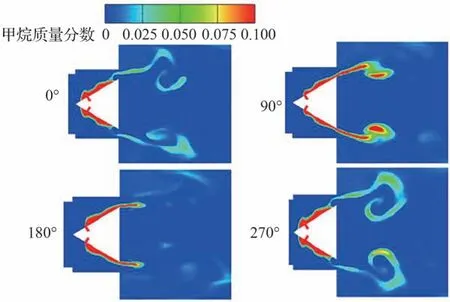
图11 工况C1 中一个周期内燃料甲烷振荡特性分布Fig.11 Distribution of fuel methane oscillation characteristics in one cycle under Condition C1
结合图12 来看,工况C1 在随着声学特性振荡时,伴随着甲烷在钝体突扩喷口间隙处的反复阻塞流动过程,形成较为轻微的回火特征。同时,随着声学振荡周期的循环,新鲜混合物来回往复流动,火焰随之发展或闪回,燃料在中心回流区的反复卷吸过程中,形成了明显的高温涡团结构。回火特征的数值预测,也显示出振荡燃烧的复杂特性。
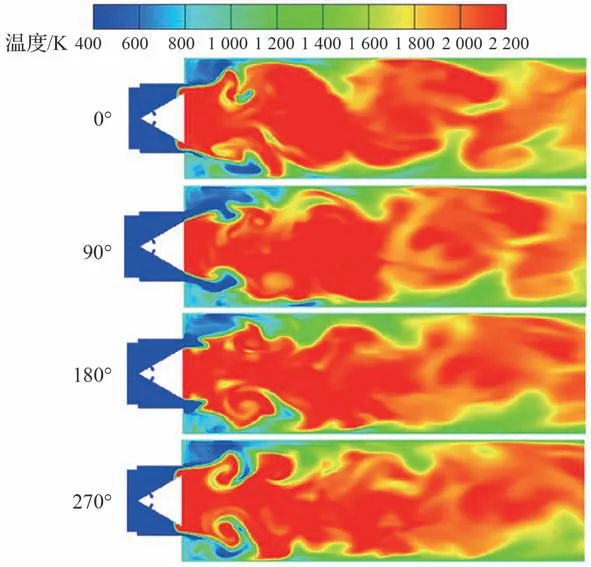
图12 工况C1 中一个周期内温度振荡特性分布Fig.12 Distribution of temperature oscillation characteristics in one cycle under Condition C1
在工况C1 中,发生极限环振荡燃烧模态后,整个狭长的燃烧室呈现轴向声学模态耦合,如图13 工况C1 中4 个压力测点的FFT 分布结果所示,各个测点的特征主频一致,振幅随着测点沿流向分布而逐渐降低。PMT1 测点的振幅1 121.1 Pa,作为上游水动力学的特征值,要高于声学振荡主频对应的975.25 Pa。此后,越靠近下游,压力脉动越弱。
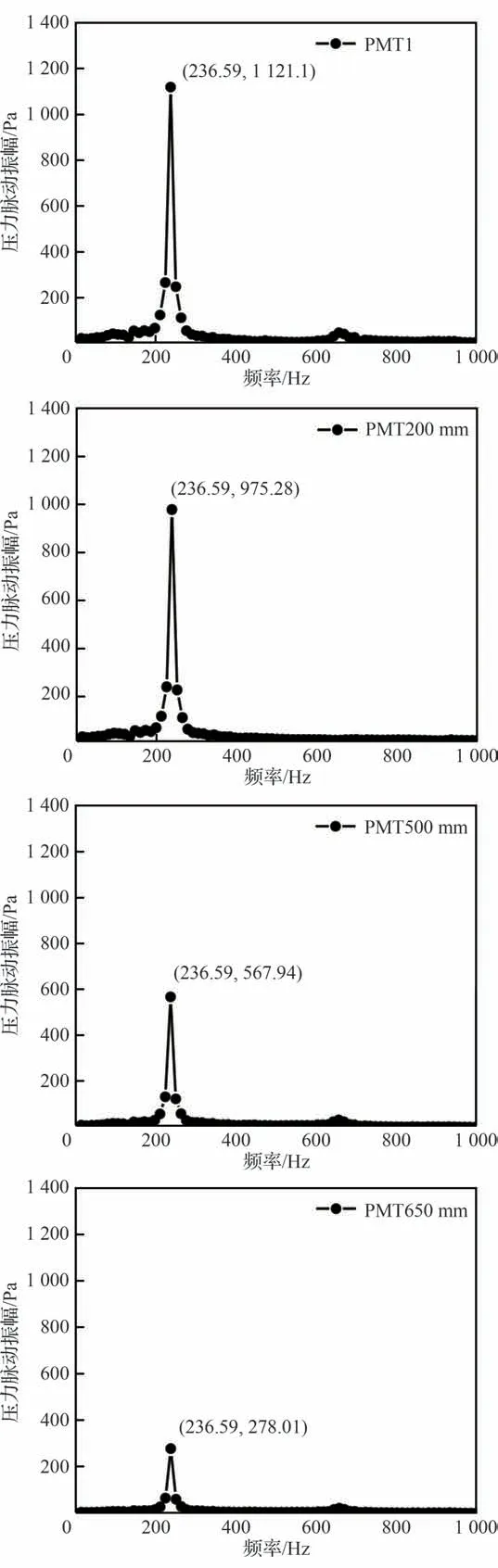
图13 工况C1 中4 个压力测点的FFT 分布结果Fig.13 FFT distribution results of 4 pressure measuring points under Condition C1
工况C3 和C1 宏观特性比较接近。但随着燃烧功率的增加,振荡燃烧时压力脉动更加剧烈,如图14 所示。工况C3 中试验测定的声学振荡主频为271.88 Hz、振幅为2 846.97 Pa,本文数值方法预测的结果分别为266.37 Hz、2 489.2 Pa,与试验值较接近;对于上游的PMT1 水动力学测点位置,数值预测的压力脉动幅值为2 828.3 Pa,大于下游的PMT200 mm 测点位置数值,但差异不大。在工况C3 中,上下游测点的压力脉动幅值数值预测结果较为接近,可能为在高功率工况C3 下,数值计算声学的影响比较强烈,已经传导至上游钝体临近喷口处,实际试验中PMT1 测点的位置要比数值计算中更加靠近上游空气进口,对湍流水动力的影响反馈也更加集中。这与工况C1 中的结果是类似的,但由于工况C3 的燃烧功率更高,振荡环模态更加充分,因此在FFT 的结果中也比工况C1 更加显著。
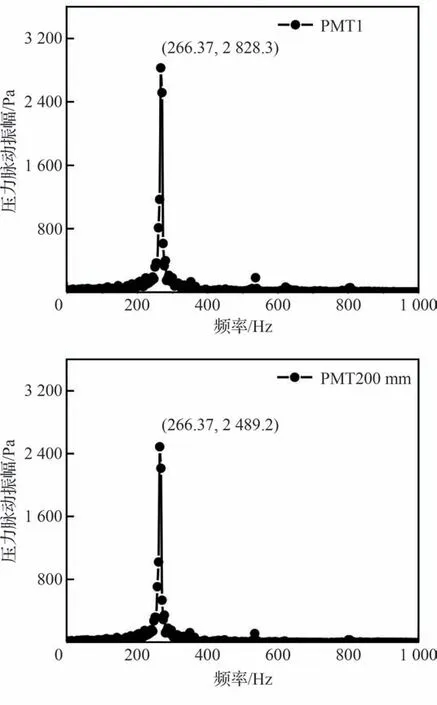
图14 工况C3 中2 个主要压力测点的FFT 分布结果Fig.14 FFT distribution results of two main pressure measuring points under Condition C3
此外,工况C3 中OH 组分和温度2 种标量场的周期性分布如图15 和图16 所示。可以看出,LIMOUSINE 燃烧室的自激振荡燃烧模态激发时,火焰会向后推移一段距离(大约为1~2倍钝体特征长度)后燃烧充分发展起来,这与试验中观察的结果比较相似[31]。OH 的分布也呈现明显的周期性特征,伴随着上述分析中的燃料掺混效果的反复,OH 组分在1~2 倍钝体特征长度的区域里随着剪切层和中心回流区而由中心向两侧壁面振荡,随后在3 倍钝体特征长的区域内形成与上一段距离相反的扩张或收缩特征,这与湍流大尺度涡系结构在振荡过程中对火焰的作用效果相吻合。
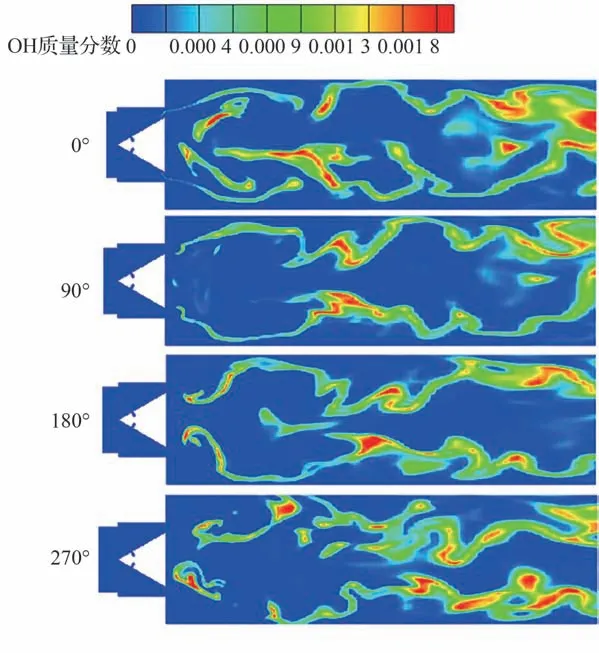
图15 工况C3中一个周期内组份OH 标量场的分布特性Fig.15 Distribution characteristics of component OH scalar field in one cycle under Condition C3
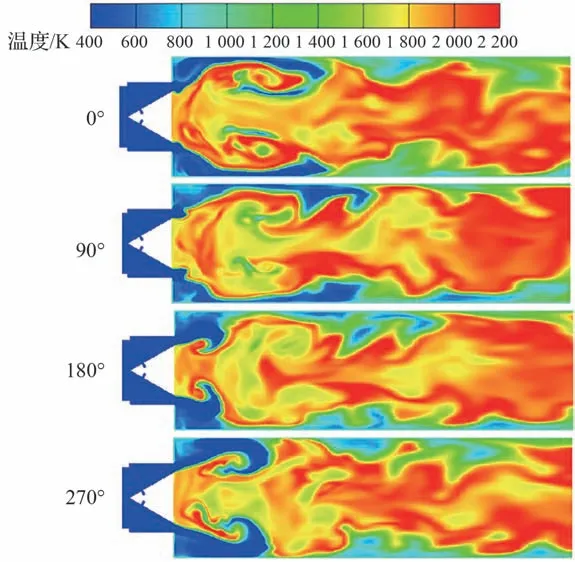
图16 工况C3 中一个周期内温度标量场的分布特性Fig.16 Distribution characteristics of temperature scalar field in one cycle under Condition C3
回火特征在工况C3 中只有轻微表现,可能是随着燃烧功率的增强,流量增大后湍流雷诺数升高,湍流对声学振荡特性的抵抗能力也随之增强,对可能造成回火的已燃高温气体向上游的阻断作用更明显。
图17 所示为工况C3 一个周期内湍流涡系的分布演化特性云图。在波峰位置时,涡管特征明显,湍流向中心回流区卷吸,并沿壁面向后发展,向上游形成肩部回流区,呈现典型的突扩后回流特征。当相位逐渐向波谷改变时,涡管被明显抑制。
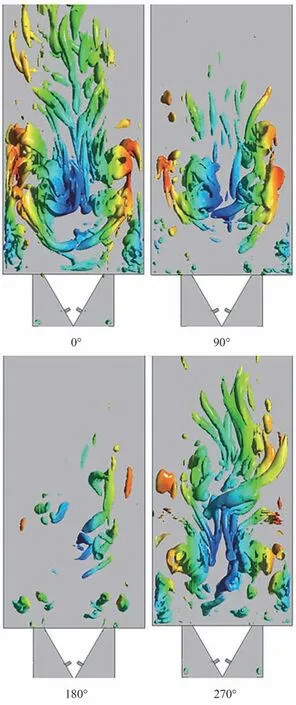
图17 工况C3 中一个周期内湍流涡系的分布特性Fig.17 Distribution characteristics of turbulent vortices in one cycle under Condition C3
3.3 过渡振荡模式工况双频特性结果
工况C1 和C3 均为极限环振荡燃烧模态工况,工况C2 较为不同,是稳定和不稳定的临界状态。本文对工况C2 利用相同的数值模拟方法作了数值研究。
主要时序信号的监测结果如图18 所示(图中HRR 表示体积热释放速率),PMT200 mm 的燃烧室压力时序信号的模态与工况C1 和C3 存在明显差异,压力在一个周期内上升时,分成2 段,第1 段斜率较高,第2 段斜率较低,之后以同一斜率下降至波谷。燃烧室更加靠后的2 个压力测点PMT500 mm 和PMT650 mm 的信号演化则趋势相同,且基本相位差较小。PMT200 mm 和燃烧室钝体上游的PMT1 以及热释放速率的监测信号间存在明显的相位差。热释放速率曲线存在二次波峰,并且间替分布。在PMT200 mm 压力脉动从波谷向波峰的振幅过程中,热释放曲线既存在波峰,也存在波谷。相比完全极限环振荡工况C1 和C3,工况C2 作为中间模态涉及的物理机制更为复杂。
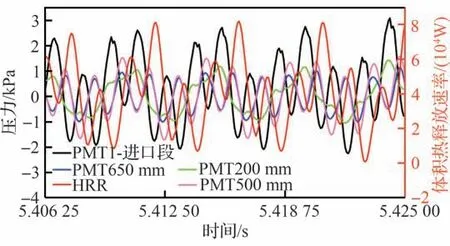
图18 工况C2中压力和热释放速率的信号时序监测变化Fig.18 Signal time sequence monitor change of pressure and heat release rate under Condition C2
试验中测量到工况C2 发生振荡的特征频率为212.81 Hz,振幅为676.54 Pa(在PMT200 mm 位置处测量)。如图19 所示,工况C2 的数值预测结果与试验相比,误差较小。不同于前述工况C1 和C3 的模式,工况C2 存在明显的双峰预测结果,且只在PMT200 mm 位置处的声学特征主频同试验保持一致。之后,声波的能量则随着向下游发展,逐渐同湍流的水动力学相耦合,在PMT500 mm 位置的高频压力振幅升高,随后在PMT650 mm 处因临近出口又略有降低。
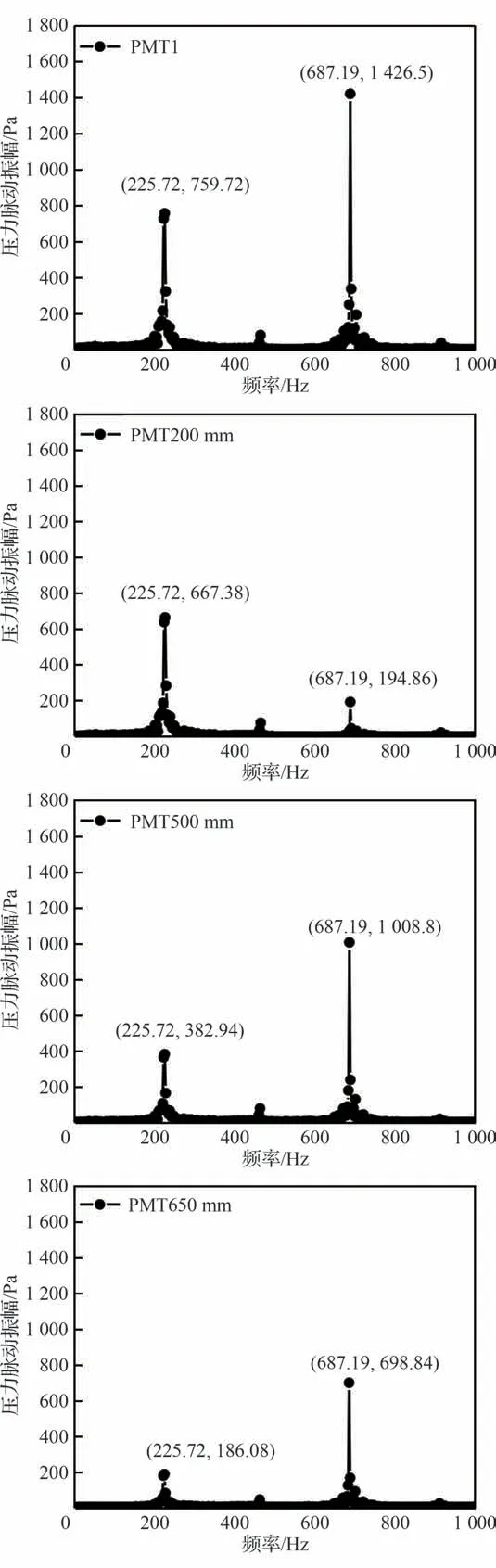
图19 工况C2 中4 个压力测点的FFT 分布结果Fig.19 FFT distribution results of 4 pressure measuring points under Condition C2
结合图20 中工况C2 的热释放速率周期分布云图来看,燃烧室中最根部位置发生典型的涡团周期振荡后,在一倍的三角型钝体特征长度下游,热释放速率趋于稳定的贴壁以波浪式发展,更下游位置的燃烧脉动较弱,和声学的振荡耦合逐渐减弱,声学模式转而和下游的已燃气体通过湍流的强烈耦合而影响整个燃烧室中低频和高频声学频率的振幅分布。
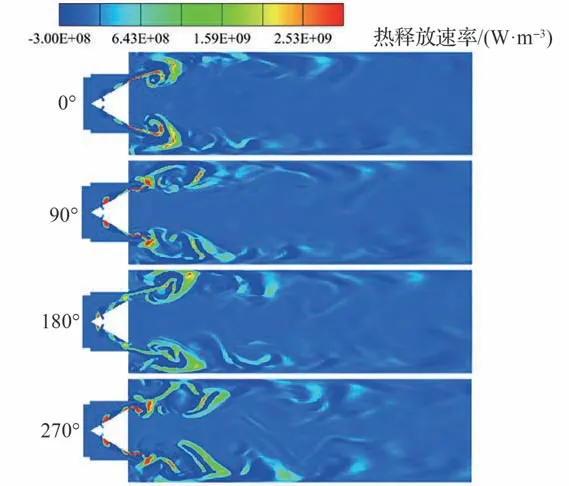
图20 工况C2 的瞬态热释放速率周期性分布Fig.20 Periodic distribution of transient heat release rate under Condition C2
工况C2 作为过渡状态,呈现复杂的热声耦合物理机制。如图21 为工况C2 一个周期内的湍流涡系分布云图。在一个周期内的涡管变化和图17 中工况C3 的趋势相同,均随着相位波峰波谷的变化呈现增强和抑制状态。尽管如此,在工况C2 中,存在明显的双层涡管发展特征,如图21中红圈部分所示。第1 层涡管在靠近上游位置,第2 层涡管自中心回流区中间,连接着第1 层涡管之后向下游发展,2 层涡管在一个周期内的某些时刻中同时存在。这也可能是工况C2 呈现双峰特征的原因。这与Han 和Morgans[5]的LES 模拟结果观测到的结果比较相似。
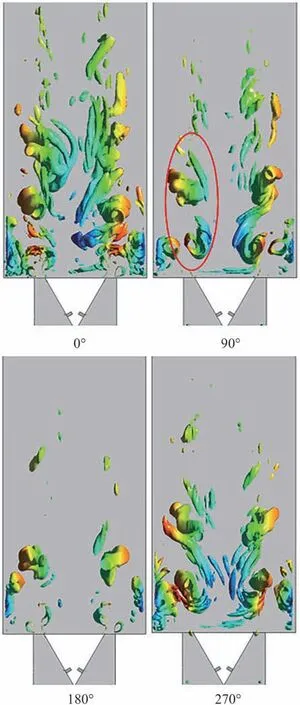
图21 工况C2 一个周期内的湍流涡系分布Fig.21 Turbulent vortices distribution in one cycle under Condition C2
4 结 论
本文在自适应湍流模拟方法SATES 框架下,发展动态模型参数的优化模型,并结合3 种不同燃烧源项封闭方法耦合可压缩详细化学反应建表FGM 燃烧模型,对LIMOUSINE 部分预混燃烧室开展了振荡燃烧数值预测和振荡模态研究,得到主要结论如下:
1) 热声振荡燃烧的数值预测结果对湍流燃烧封闭源项方法具有较高的敏感性,不同的源项封闭方法由于湍流火焰燃烧速度预测结果不同,直接影响声学模态的耦合方式及振荡燃烧的结果。
2) 在自适应湍流模型SATES 模化框架下,有限速率模型(W1)、Zimont(W2)和Fureby(W3)3 种燃烧模型对振荡特征主频预测结果均较好,但有限速率和Zimont 方法预测的压力振幅结果远高于试验值,Fureby 模型的结果则与试验值吻合良好。
3) 部分预混的振荡燃烧数值预测精度一方面受燃烧模型影响,另一方面受湍流掺混效应的影响,特别是对振荡幅值的影响较大。燃烧过快或过慢可能会由于主体对象不同(如已燃气体或燃烧释热),引起不同类型的热声耦合过程。
4) 不同工况下的振荡燃烧模态预测存在差异。完全振荡模式下数值预测趋于单一的轴向模态特征主频分布;过渡振荡模式下,数值预测的模态存在明显的双峰分布特性。
5) 振荡燃烧的单峰和双峰特征呈现不同的涡系耦合机理,双峰特征中存在着双层涡旋管结构。
