航空发动机燃烧不稳定性预测及控制研究进展
2023-08-31孙晓峰张光宇王晓宇李磊邓向阳程荣辉
孙晓峰,张光宇,王晓宇,李磊,邓向阳,程荣辉
1.北京航空航天大学 能源与动力工程学院,北京 100191
2.北京航空航天大学 航空发动机研究院,北京 100191
3.中国航发商用航空发动机有限责任公司,上海 200241
4.中国航发沈阳发动机研究所,沈阳 110015
燃烧不稳定性问题是由燃烧室内燃烧火焰所产生的非定常热释放和声波充分耦合的结果,广泛发生在多种燃烧动力系统中,如固/液火箭发动机、地面燃气轮机、锅炉、冲压发动机、军用航空发动机及民用航空发动机等[1-3]。该问题发生时具体表现为大幅度的压力脉动,影响燃烧室壁面正常冷却换热,且会造成燃烧室壁面结构疲劳损坏,甚至会引起燃烧室壁面烧蚀,导致动力系统彻底失效。该问题早在20 世纪30~40 年代固/液火箭发动机、航空发动机加力燃烧室[4]的研制过程出现,并在20 世纪60 年代美国“阿波罗”登月计划土星五号F-1 火箭发动机[5]的研制中开始得到广泛关注。随着推进动力系统的迭代演化,该问题的具体特征也在不断变化,且一直是航空航天燃烧动力系统中的关键瓶颈难题。
近年来,随着军用、民用航空发动机分别朝着高推重比、低污染物排放方向继续发展,燃烧不稳定性问题也愈加复杂[6-7]。2 类发动机燃烧室特性如表1 所示,对于军用发动机,为了满足先进战机更宽的飞行包线,其加力燃烧室的结构更加紧凑,能量密度更大[8];此外,由于进口温度的提高,燃油点燃延迟时间更短,燃油和空气到达火焰前锋前没有充分的时间均匀混合,更易发生燃烧不稳定性[9],且燃烧不稳定性呈现多频率、多模态的复杂特征,使得控制手段的设计更具挑战性。与此同时,出于对环境保护的考虑,民用航空发动机对低排放要求更加严格,具有低排放特征的贫油预混预蒸发(LPP)燃烧室得到广泛应用[10],但是此种燃烧室工作在贫油熄灭边界附近,更易受到扰动影响,也更容易出现燃烧不稳定性。在中国及西方军、民用航空发动机型号的研制过程中,均遇到严重的燃烧不稳定性问题,且在可预见的未来发展型号中,该问题仍是需要攻克的重点难题。为了在新型航空推进系统研制过程中,排除燃烧不稳定性问题,有必要对其发生机理进行深入研究,并在此基础上突破传统控制思路,发展合适且具有工程适用性的先进控制手段,并融入到发动机的设计体系中,避免重走“先出现、后解决”的高成本老路。

表1 2 种燃烧室内涉及燃烧不稳定性问题特点Table 1 Characteristics relating to combustion instabilities of two combustors
事实上,燃烧不稳定性问题的基本发生机理是十分清晰的。早在1878 年,Rayleigh 就对燃烧不稳定性发生机理给出了解释[11],提出了著名的Rayleigh 准则,即当燃烧系统内的非定常热释放与声波同相位时,热能转化为声能,在有限短时间内,系统内的声能量急剧增加,如果系统热声耦合增加的声能量大于系统内声耗散量,燃烧不稳定性就会发生;反之,声能则会转化为热能,燃烧不稳定性得到抑制。实际燃烧室中,声波和燃烧非定常热释放干涉关系的建立,通常需要流动的参与,如图1 所示,燃烧室内流动扰动会引起火焰面积的脉动,产生非定常热释放,非定常热释放引起气体体积的脉动,充当单极子声源,发出声波,声波带来的压力扰动影响燃烧室进口空气量、燃油流量及当量比的脉动,从而形成封闭的反馈环。在此过程中,如果声波反射涉及到燃烧室进出口边界,则为耦合燃烧室声腔的燃烧不稳定性;如果参与反馈的声波不涉及燃烧室进出口边界的反射,则为固有燃烧不稳定性[12-13]。因涉及的反馈机制不同,对2 种燃烧不稳定性的控制思路也有差异,本文重点关注工程实际中经常出现的耦合燃烧室声腔的燃烧不稳定性。

图1 热声反馈环示意图Fig.1 Illustration of thermoacoustic feedback loop
基于燃烧不稳定性基本发生机理,控制燃烧不稳定性可以从2 个方面入手:① 削弱热声耦合驱动;② 增加系统声学耗散。尽管控制思路已经十分清晰,但是面对实际发动机的燃烧不稳定性控制,仍有不少困难需要解决。实际航空发动机燃烧室工作环境复杂,工况变化范围大,不同状态下,燃烧系统的燃烧区域及边界处流动均有较大差异,如军用航空发动机加力燃烧室在不同马赫数及高度状态下,进口来流的马赫数和温度均不同,且不同的加力状态,燃油喷射位置也有差异,这会导致完全不同的钝体火焰形态及燃烧区域的热声耦合强度,因此通过对包括燃油供油规律和喷油位置的调整、火焰稳定器/旋流器的结构设计来削弱热声耦合强度的控制设计需要配合大量整机试验进行验证。另外,无论是加力燃烧室还是民用环形燃烧室,不同工况下的火焰形态会导致燃烧室内占主的燃烧不稳定模态也不同,大推力的加力燃烧室的燃烧不稳定模态呈纵向、横向(包括径向及周向)等多模态及其复合模态特征,因此通过增加系统的声学耗散,包括增加壁面、内部吸声装置及调整进出口声学边界等手段,来抑制燃烧不稳定性的发生需要针对具体的不稳定模态及频率特征进行设计优化。面对先进航空发动机燃烧室的控制设计,需要针对性地发展针对不同尺度问题的先进研究方法认识系统的非定常系统特征。
燃烧不稳定性问题是涉及燃烧化学反应、湍流流动及声波等多空间、多时间尺度的复杂问题,对燃烧不稳定性问题的动态特征进行准确刻画一直是领域内重点研究的课题。关于燃烧动力系统的不稳定性,最早在1941 年,冯·卡门就提出通过延迟时间进行解释[14]。随后,Crocco 和Cheng[15]建立了著名的n-τ火焰延迟时间理论,并得到广泛引用。研究人员开始认识到,火焰对扰动的非定常响应作用是燃烧不稳定性问题发生的关键。Zinn[16]借助n-τ模型发展了非线性液体火箭发动机燃烧不稳定性模型,随后Zinn 和Lores[17]发展了伽辽金方法求解燃烧不稳定模态。加力燃烧室中的火焰依靠钝体进行稳定,其中,跟钝体火焰相关的非定常流动作为火焰延迟时间的重要来源得到大量研究[18]。Rogers 和Marble[19]试验研究发现,加力燃烧室的高频燃烧不稳定性是钝体火焰稳定器后涡脱落和燃烧室声波形成反馈导致的。Lovett 等[20]对钝体火焰中的燃油雾化特性、钝体火焰特性及燃油分布特性开展了大量研究,据此,Lubarsky 等[21]提出通过新型火焰稳定器结构优化燃油分布控制燃烧不稳定性。Lieuwen 等[22-24]进一步研究了钝体火焰非定常流动特性,特别是钝体火焰在纵向、横向声激励条件下的流场和火焰响应特征。研究发现,火焰前后密度比对于钝体火焰后流场影响较大,当前后密度比低时,燃烧流场尾迹更接近于冷态流场,会有大尺度交替出现的卡门涡街出现,当密度比高时,则有对称性的、曲张的小尺度涡结构[24]。燃烧流场的流动特性及受声激励的响应特征,影响火焰延迟响应特征,进而决定发生热声振荡时的热声耦合强度。
不同于加力燃烧室的高速流动依靠钝体形成的回流区稳定火焰,目前商用航空发动机常用的旋流火焰通过旋流器形成回流区,且燃料和空气经过预混预蒸发,形成贫油预混燃烧模式,该类燃烧室工作区域靠近贫油熄灭边界,火焰对扰动更为敏感,也更容易发生燃烧不稳定性。为了研究该类燃烧室环境及燃烧模式下的燃烧振荡特性,EM2C 实验室[25]搭建了模型实验室深入研究了旋流火焰的动态响应特性,对火焰描述函数进行了大量的测量。随后,剑桥团队[26]和EM2C实验室[27]分别搭建了环形模型燃烧室,研究了在环形燃烧室多火焰的设计结构下,燃烧不稳定模态的特征。并在模型燃烧室中证实了旋转模态、驻波模态及二者混合模态的发生会受到非线性过程及非对称性的影响[28]。该类研究充分揭示了环形燃烧室内燃烧不稳定性的独特特征,为认识其机理及发展控制方法提供了指导价值。然而,真实环境下的燃烧室工作在高温高压,且会受到上游压气机出口叶片排和下游涡轮叶片排的声学反馈影响[3],需要在试验研究及模型研究中进行考虑。
燃烧不稳定性问题是系统耦合性问题,其特征受到真实流动条件,如高温高压及高流速,复杂边界条件及复杂燃烧火焰,如环形燃烧室多头部火焰干涉等因素的影响。因此,真实发动机的燃烧不稳定性问题的出现及特征,往往需要在整机发动机试车中才能暴露。而对该问题进行预测,目前工程上可行的方式依然是通过对复杂尺度问题进行简化,如燃烧火焰的非定常响应特性通过试验或者数值模拟方法进行模型化处理,其余部分则通过基于声网络的模型进行刻画。而对于燃烧不稳定性的控制,通过对火焰区域的调整,如果控制一个模态,则另一个模态可能会被激发[29]。工程可实现的仍以被动控制方法为主,特别是穿孔板声衬在军用加力燃烧室和民用环形燃烧室中均得到广泛应用,对相关被动控制的设计也需要发展模型方法在设计阶段进行考虑。
综上所述,对航空发动机燃烧不稳定性问题的研究,首先需要认识燃烧室内非定常耦合机理,并发展工程适用性强的模型工具,能够对系统的燃烧不稳定性进行快速预测及控制设计。为此,本文从以下3 个方面展开:① 燃烧室非定常流动及火焰响应特性;② 燃烧不稳定性声网络预测分析模型;③ 考虑声软壁面控制的三维燃烧不稳定性预测控制模型。在了解燃烧不稳定性问题的研究进展的基础上,重点强调建立包含非定常系统、非定常热释放及复杂声边界的三维模型的重要性,并对未来需要研究解决的燃烧不稳定性关键问题进行展望。
1 燃烧室非定常流动及火焰
燃烧不稳定性耦合问题的复杂性来源于其内部的湍流流动及燃烧。火焰的稳定燃烧需要在气路流道里产生低速回流区,才能稳定火焰,释放热能。复杂流动及燃烧在紧凑密闭、高温高压的极限条件下,更易发生流动、燃烧、声学的耦合作用,促使燃烧不稳定性问题的发生。为了理解燃烧不稳定问题的发生机理,学术界开展了大量关于燃烧室非定常流动及火焰非定常响应的试验及模型工作,以从机理上认识燃烧不稳定性热声耦合的来源,便于指导燃烧室的设计。
1.1 加力燃烧室非定常流及钝体火焰
加力燃烧室内用于稳定火焰的结构为钝体火焰稳定器。根据发动机的不同,钝体稳定器的结构略有不同,但是总的设计思想是通过钝体将主燃烧室燃烧过后的热气流进行二次喷油,在钝体稳定器后方形成低速回流区来稳定燃烧。相比于民用发动机的旋流燃烧室,该类型燃烧室流速更高,流动、燃烧及声波之间的干涉机制更加复杂,至今,研究人员仍然难以完全清晰认识该类问题的物理过程。
早期对钝体火焰的研究[30-31]主要关注火焰的静态稳定燃烧问题,即根据燃烧室内时间平均参数确定火焰的稳定燃烧边界。特别地,研究发现[30],作为表征加力燃烧室工况变化的一个重要参数,进气温度对回流区影响较大,例如,未燃气体温度提高1 倍后,回流区长度会减少15%~20%。早期的研究帮助人们对钝体火焰燃烧的时间平均参数特征及稳焰机制建立了基本认识。事实上,加力燃烧室流动的非定常特性极强,需要针对钝体流场及火焰开展瞬态非定常特性研究。
钝体火焰的非定常脉动特性,主要受到流动的非定常作用影响,包括声波和涡对火焰面的影响作用。特别以大尺度的涡结构引起火焰面的脉动为主。而钝体火焰涡结构的来源主要包括2 个方面[22]:① 钝体尾缘的剪切层受Kelvin-Helmholtz (K-H)不稳定性影响表现为对流不稳定性,剪切层后方形成间距紧凑的涡结构;② 钝体尾迹流动受Bénard/von-Kármán (BVK)不稳定性的影响会表现为绝对不稳定性,如图2[22]所示,在不考虑火焰燃烧的影响,等温钝体后方尾迹出现非对称交替脱落涡,频率为
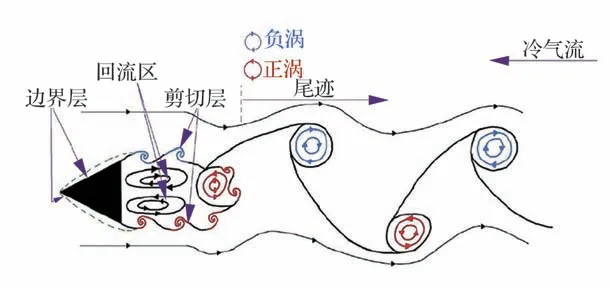
图2 等温钝体流场示意图[22]Fig.2 Instantaneous topology of an isothermal bluff body flow[22]
式中:St为斯特劳哈尔数;U为钝体尾缘平均速度;D为钝体的特征尺寸。当考虑燃烧发生时,钝体尾迹流动的这种非定常特征会受到影响,燃烧火焰热释放改变了火焰面前后的密度比ρu/ρb,进而抑制了BVK 涡街的这种非对称结构,从而使得剪切层K-H 不稳定性占主导地位。而当进气温度较高时,ρu/ρb会降低,此时,流场更加接近无燃烧反应流场非定常特征,BVK 不稳定性占主导地位。对应于实际加力燃烧室,在高马赫数状态下,进气温度较高,燃烧室内钝体流动会受到BVK 不稳定性的影响,进而影响燃烧不稳定性特征频率。
钝体火焰的非定常特性,引起气体体积脉动,在声学上可以类比为单极子声源[32],脉动火焰产生的声波在封闭燃烧室环境内,会经过边界反射进一步影响钝体火焰流动及火焰,这就带来了声波激励下的钝体火焰响应问题。研究表明声波对钝体火焰的影响主要是间接通过激起涡结构影响火焰面的脉动[33]。现代加力燃烧室常出现低频纵向模态及高频横向模态,因此,有必要分别研究纵向声模态及横向声模态激励下的钝体火焰响应特性。Emerson 和Lieuwen[23]研究发现,钝体火焰在纵向声波激励下,2 种扰动模式参与影响火焰脉动响应:① 受剪切层K-H 不稳定性影响的对称V 模态(Varicose Mode);② 受BVK 不稳定性影响的非对称S 模态(Sinuous Mode)。图3[23]给出了不同声激励频率下,2 种模态沿轴向的能量分布占比,可以发现,在钝体附近,V 模态能量主导。当激励频率等于或接近尾迹脱落涡频率时,随着下游距离的增加,S 模态的能量占主导。该结果表明,S 模态能量在共振频率激励下主导,在非共振条件下,则V 模态能量主导。

图3 在不同激励频率下S 模态能量占S 模态和V 模态总能量的比值沿轴向的分布[23]Fig.3 Axial distribution of ratio of Sinuous mode energy to total energy of Sinuous mode and Varicose mode at different forcing frequencies[23]
实际上,钝体火焰正是由于不同非定常流动模态的干涉影响,其在声激励下的非定常热释放现象会有出人意料的表现特征,如图4[23]所示的钝体后方不同位置处,局部的非定常热释放随激励频率的变化情况显示,当激励频率等于尾迹脱落涡频率时,非定常热释放最小。
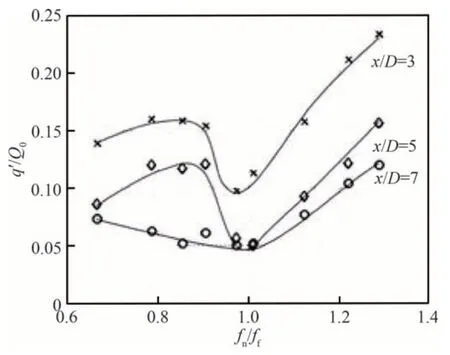
图4 局部非定常热释放幅值随激励频率的变化[23]Fig.4 Variation of local unsteady heat release amplitude with forcing frequency[23]
这其实是受到S 模态的非对称结构导致的钝体尾缘后方上下2 个火焰非定常热释放脉动相位相反相消的结果。为了认识加力燃烧室在发生横向燃烧不稳定模态问题时钝体火焰的特性,研究者也开展了针对钝体火焰在横向声模态激励响应特性的研究[34],发现火焰的响应是受到声激励产生的速度扰动以及引起的涡致速度扰动叠加的作用效果。
以上研究帮助理解了钝体火焰的非定常流动特征以及与其与声波相互作用的机制。针对此类理想模型燃烧室的钝体预混火焰,可以通过试验数据构建火焰参数模型[35],也可以用G函数方法[36]构建火焰响应模型,作为系统燃烧稳定性预测的关键模型。但是,这些研究并没有考虑加力燃烧室的实际工作条件,包括燃油特性及喷射方式等,这些因素均会影响钝体流动及火焰形态。对于先进加力燃烧室,由于进气温度更高,而且燃油自燃延迟时间更短,因此,喷油杆通常会与火焰稳定器进行一体化设计,一方面便于喷油杆的冷却,另一方面减小燃油与空气掺混对流时间。另外,隐形发动机设计要求使得涡轮后支板倾斜旋转,能够起到遮挡高温部件的作用,但是会引起加力燃烧室进口呈旋流流动,这对于钝体流动以及火焰响应问题的具体影响也是不清楚的。
通过对局部燃油喷射位置的调控抑或是对火焰稳定器的结构设计,也许在某些工况可以抑制燃烧不稳定性,但是这类控制设计方法,因为没有完全普适的规律,并不能在宽工况范围内保证控制效果。因此,面向新型航空发动机加力燃烧室的燃烧不稳定性控制问题,需要针对钝体流动与钝体燃烧火焰等基础问题,开展更深入的研究。
1.2 旋流火焰非定常响应
目前民用航空发动机广泛采用LPP 燃烧室[37],该类燃烧室氮氧化物排放低,但更容易出现燃烧不稳定性。预混旋流火焰通过旋流器产生具有周向速度分量的旋流产生低速回流区以稳定火焰。相比于加力燃烧室,民用航空发动机的旋流燃烧室平均流速较低,且旋流火焰也更加紧凑,火焰的非定常响应特性更容易通过火焰传递函数(用于预测线性稳定性)或火焰描述函数(可用于预测极限环幅值)来刻画,且将该类火焰模型运用在燃烧不稳定性问题的预测已是比较成熟的方式。本文不再赘述旋流非定常流动,关于此方面的内容可以参考文献[38-40]。
对旋流火焰的研究工作,重点在于得到代表旋流火焰的非定常响应特性[41]的火焰传递(描述)函数,方便与其他低阶声网络模型或者数值计算方法建立燃烧不稳定性理论预测模型。法国EM2C 团队在此方面开展了大量模型试验及理论模型工作[42-43],提高了对旋流火焰的物理认识。如图5[44]所示,通过搭建旋流燃烧模型试验台,引入光学、声学测试手段,可以得到旋流火焰在不同声激励频率、幅值下的非定常热释放特性,即得到旋流火焰的火焰描述函数。为了认识旋流火焰的非定常响应物理机制,Palies 等[44]根据Cumpsty 和Marble 激盘模型[45],对旋流器建立匹配条件,从而得到旋流器在受到声波扰动后,一方面会产生轴向声速度,引起旋流器出口形成涡,涡对流传播引起下游火焰卷曲,产生非定常热释放,另一方面会产生周向速度扰动,表现为旋流数扰动,引起火焰角度的扰动,产生非定常热释放,如图6[43]所示。以上2 种机制的叠加干涉形成了最后的火焰描述函数的增益具有极大极小值的特点,如图5(b)[44]所示。
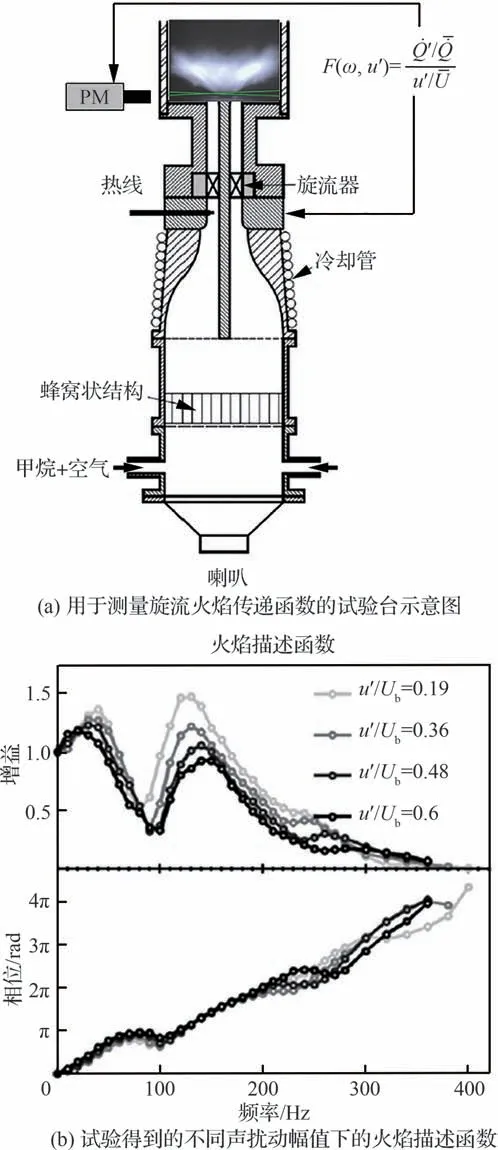
图5 旋流火焰试验台及火焰描述函数[44]Fig.5 Experimental configuration of swirling flame burner and flame describing function results [44]

图6 旋流火焰非定常热释放产生机理[43]Fig.6 Mechanisms generating unsteady heat release rate fluctuations in swirling flows[43]
通过线性火焰传递函数即可完成对燃烧不稳定性发生的预测,但是如何预测燃烧不稳定性幅值?这一问题的简化解决得益于Dowling[46]、Noiray 等[47]对火焰非线性响应的研究。多数情况下,燃烧不稳定性问题发生后达到非线性饱和,仍可以用线性声学刻画,而该问题的非线性主要来源为火焰对不同幅值入射声波的响应,因此,对不同幅值入射声波下火焰非定常响应的研究,得到旋流火焰的火焰描述函数,丰富了燃烧不稳定性非线性幅值预测的研究工具。
实际环形燃烧室具有周向分布的多个旋流器,多个旋流火焰之间会发生干涉,因此,单旋流燃烧试验得到的火焰传递函数,在某些情况下,并不能在实际中完全适用。Fanaca 等[48]通过试验测量并比较单旋流燃烧火焰和环形旋流燃烧火焰流场及火焰形态发现,在不同的受限空间边界条件下,单旋流火焰流场形态受到燃烧室壁面的影响,流场呈现“壁面射流(Wall Jet)”,即出现较大射流角度,可以明显观察到旋流射流与壁面的作用,而在具有多个旋流的环形燃烧室环境下,其中某个旋流器的流场呈“自由射流(Free Jet)”形态,旋流射流角度较小,如图7[48]所示。这种受旋流侧方边界条件不同引起的流场形态的差异是导致在不同试验台下测得不同火焰动态响应的原因。该研究通过给出旋流器和燃烧室的横截面积比Acc/Abu用于量化旋流火焰受边界影响多少来确定旋流火焰形态切换边界,用于指导在何种条件下可以将单旋流试验的火焰特性应用于多火焰的环形燃烧室中。
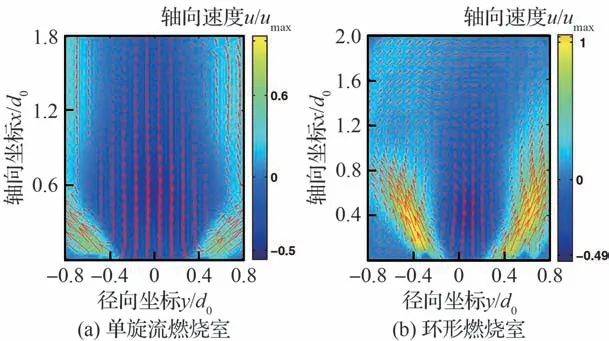
图7 流场轴向速度PIV 结果 [48]Fig.7 PIV results of axial velocity of flow field[48]
事实上,单旋流试验的结果是否能够直接应用于环形燃烧室的燃烧不稳定性预测,取决于多个因素,包括单旋流试验台的具体几何尺寸,旋流的声波激励模式以及工况条件[49]。在不同的声激励条件及旋流试验台上,单旋流的动态结果与多旋流试验台下的动态结果可能并无差异[50]。
尽管大量旋流火焰相关研究已经为认识航空发动机燃烧不稳定性机理起到重要作用,但是涉及更真实发动机燃烧室环境,例如高温高压下多火焰干涉问题,涉及非线性耦合的多频率激励下的火焰响应问题[51-52],多模态干涉问题[53],以及通过声激励旋流火焰得到的传递函数是否能够代表发生燃烧不稳定性时的火焰特性[54],这些都需要进一步深入研究来澄清回答。
2 燃烧不稳定性声网络预测分析模型
目前,得益于数值计算能力的提高,将大涡模拟(LES)用于预测真实燃烧室的燃烧不稳定性已得到证明并取得了显著进步[55-56],可作为燃烧试验的辅助手段解释燃烧不稳定模态的产生及演化机理。然而,将之应用于工程设计,特别是重复性的优化设计,仍有不少距离。因此,基于燃烧不稳定性问题的发生尺度为声波波长尺度的考虑,通过对燃烧系统进行合理的模型简化,形成便于计算,物理概念清晰的燃烧不稳定性声网络解析预测模型成为学术界及工业燃烧室设计研究常用的技术手段[57-58]。
如图8[58]所示,将航空发动机燃烧室经过合理的模型简化,形成一些系列串联或并联的直管道,将进口压气机出口导向叶片及出口涡轮进口导向叶片处设置为声学边界条件,在不同部件界面处建立守恒匹配方程,将火焰传递函数用于建立火焰及燃烧室声学的耦合关系,最后形成一组封闭的控制方程组,该动力系统的稳定性,可以通过求解特征值问题进行分析[59]。通过以上模型方法,形成特征值问题:
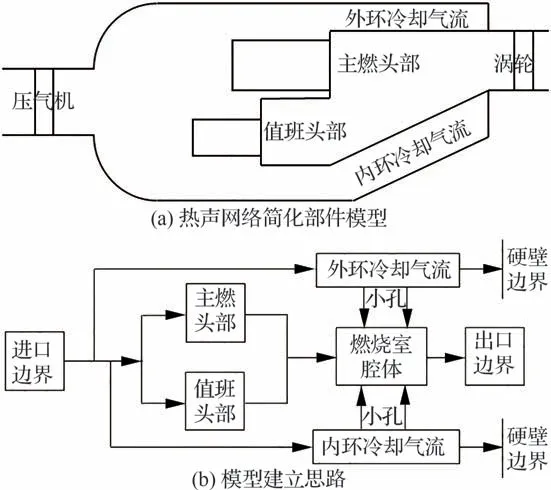
图8 航空发动机主燃烧室的热声网络模型原理示意图[58]Fig.8 Schematic diagram of thermoacoustic network model of an aero-engine combustor chamber[58]
式中:ε包含M个实参数,如燃烧室的几何尺寸,气动热力学平均参数,包括不同部件内的声速、平均流速及平均温度等;L为关于ε和ω的解析函数̂为决定系统内声模态的幅值向量。通过求解det [L(ε,ω)]=0 即可以得到系统的复数特征频率ω=ωr+iωi,其中ωr表示系统的特征频率,在扰动时间依赖项为eiωt的假设下,-ωi表示系统的增长率,其为正,表示系统不稳定性,反之,则系统稳定。
可将特征频率代入式(2),得到对应的特征模态分布情况。为了形成评估稳定性的特征值问题,需要进行以下步骤:① 将燃烧室简化为一系列的直管道,从而可以得到其内部的解析声波描述形式;② 将不同直管道进行匹配,并在匹配界面建立匹配方程,从而建立起不同部件内声扰动关系;③ 选取合适的火焰传递(描述)函数,用于建立热声耦合关系;④ 确定进出口声学边界条件,封闭方程。以较简单的一维燃烧系统(如图9所示)为例进行描述,二维和三维模型问题可以据此进行拓展。

图9 一维燃烧系统简化示意图Fig.9 Simplified schematic diagram of one-dimensional combustion thermoacoustic system
图9 中居中的红色实线表示紧致火焰面,火焰距离管道左端进口l1,距离管道右端出口l2,下标“1”和“2”分别表示未燃低温区域和已燃高温区域。火焰上游区域平均温度为,火焰下游区域平均温度为表示火焰单位面积的非定常热释放。这里采用n-τ火焰模型,即管道左端、右端声波反射系数分别为R0和RL。管道的半径相对于关注声波波长很小,因此考虑的声波仅限于平面波。管道内声波传播参考点,以及声波声压幅值系数参考图9 中示意,在马赫数为0 的近似条件下,火焰上下游的声波可以写为
式中:k1,2=ω/表示波数。根据火焰前后压力连续和流量连续条件[60],得到火焰面(x=l1)处匹配条件为
由式(5)~式(8)可以得到系统特征方程为
通过求解式(12)即可得到系统的复特征频率并对该一维燃烧系统的燃烧不稳定性进行分析。值得一提的是,传统意义上,所关注的燃烧不稳定模态为耦合燃烧室声腔的模态,而事实上,火焰处耦合建立的反馈机制导致一种特殊的固有燃烧热声不稳定模态也会产生[12-13]。考虑一种特殊的情况,即该燃烧系统的进出口边界声反射系数为0,则可以求得系统的固有热声不稳定模态的特征频率为(2n+1)π/τ(n为整数),增长率为目前,已有模型试验研究[61]证实该固有热声不稳定模态的发生,真实航空发动机是否会受到该模态的困扰还有待更多试验结果的证实。
基于声网络模型的燃烧不稳定性预测方法,根据发生机理对其中不同尺度问题分开处理,形成一种工程适用性强的分析工具。面向更容易出现周向不稳定模态的环形燃烧室,可以将周向扰动模态包含进来,发展二维燃烧不稳定性预测模型对包括轴向、周向及二者耦合复合模态进行稳定性分析[62-65],包括Helmholtz 共振器等集总参数的控制手段研究[66],不同头部热释放响应组合的控制方法研究等[67]。特别地,研究发现[63],当考虑纯周向模态问题时,声波和热释放相互干涉,火焰面前后的周向速度扰动连续导致涡波产生,在平均流速较大时,忽略涡波会导致对系统燃烧稳定性判断出现较大误差,如图10[63]所示。
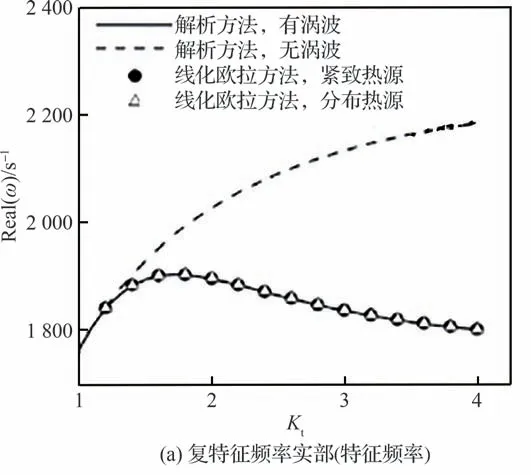
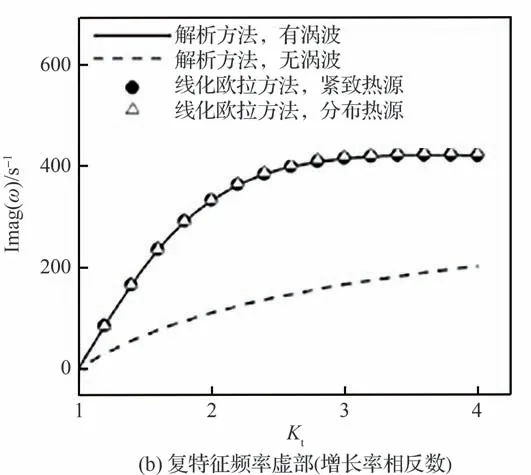
图10 复特征频率随火焰前后温度比的变化[63]Fig.10 Complex eigenfrequencies as a function of temperature ratio across flame [63]
以上综述的预测模型主要是针对硬壁面条件下的燃烧不稳定性预测,然而,实际发动机燃烧室的壁面通常开有小孔,从压气机引入冷气对燃烧室壁面进行冷却。这在声学上形成了声软壁面,引发模态散射及声学耗散,为了准确考虑壁面声耗散边界的影响,有必要建立三维模型耦合考虑声软壁面的影响,指导设计壁面声耗散以更好地控制燃烧不稳定性。
3 考虑声软壁面控制的三维燃烧不稳定性预测控制模型
燃烧室中横截面面积跳跃处,比如旋流器和进气腔、旋流器与燃烧室腔体界面处都会引发径向模态耦合问题。此外,燃烧室壁面的含冷却气流的穿孔声衬结构在声学上为声软壁面,和燃烧室硬壁面界面处存在径向阻抗边界条件的跳跃,也会引起径向模态耦合问题,如图11 所示。因此,从模型的完备性考虑,有必要建立包含声软壁面及面积跳跃的三维燃烧不稳定性模型。

图11 径向模态耦合示意图Fig.11 Schematic diagram of radial modal coupling
另外,硬壁面条件下的一维或者二维燃烧不稳定性模型可以用于分析可能的燃烧不稳定性模态及频率,并得出不稳定模态受不同参数的影响规律,却不能用于对燃烧室不稳定性壁面控制效果进行直接研究设计。这是因为,声软壁面的引入会通过改变系统的边界条件改变燃烧系统的特征频率,用硬壁面条件下预测不稳定频率结果,再针对该不稳定频率设计声学抑制器,这样解耦的方式难免会引起误差。因此,需要建立三维模型耦合考虑声软壁面的影响,才能研究并优化壁面控制效果。
3.1 均匀穿孔板声衬控制效果
声软壁面的抑制效果与燃烧室内发生的特征模态息息相关。对于加力燃烧室内常出现的纵向不稳定模态,为了研究声软壁面的抑制机制及效果,可以通过搭建模型燃烧室进行研究,如图12[68]所示。借助传递单元方法,建立了能够分析声衬对纵向不稳定模态抑制效果的解析模型,理论分析了不同声衬参数对燃烧不稳定性的影响效果。试验结果如图13[68]所示,安装有偏流的穿孔板声衬后,系统的燃烧不稳定性导致的脉动压力在所研究的当量比范围内均有大幅下降。
图12 模型燃烧室试验台[68]Fig.12 Experimental setup of model combustion chamber[ 68]
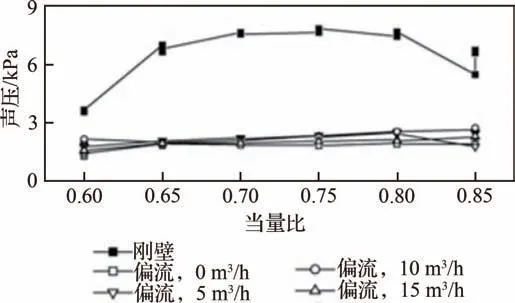
图13 不同偏流大小的声衬下燃烧室声压随当量比的变化 [68]Fig.13 Variation of sound pressure level in combustion chamber with equivalence ratio for liners with different bais flows[68]
为了建立三维模型,需要得到燃烧室内的三维声波描述[69],以一个简化的环形燃烧室为例,如图14[70]所示,该燃烧室模型由一个环形进气腔、Np个旋流器和一个环形燃烧室腔体组成,旋流器周向均匀布置在2 个环形腔体的平均半径处。进气腔内外环半径分别表示为和,长度为L0。旋流器长度为L1,直径为Dp。燃烧室腔体内外环半径分别表示为和,长度为Lc。有背腔的穿孔板声衬布置在燃烧室腔体的内外环壁面上,且内外环声衬具有相同的长度和轴向位置。声衬前缘距离旋流器出口L2,声衬长度为L3。
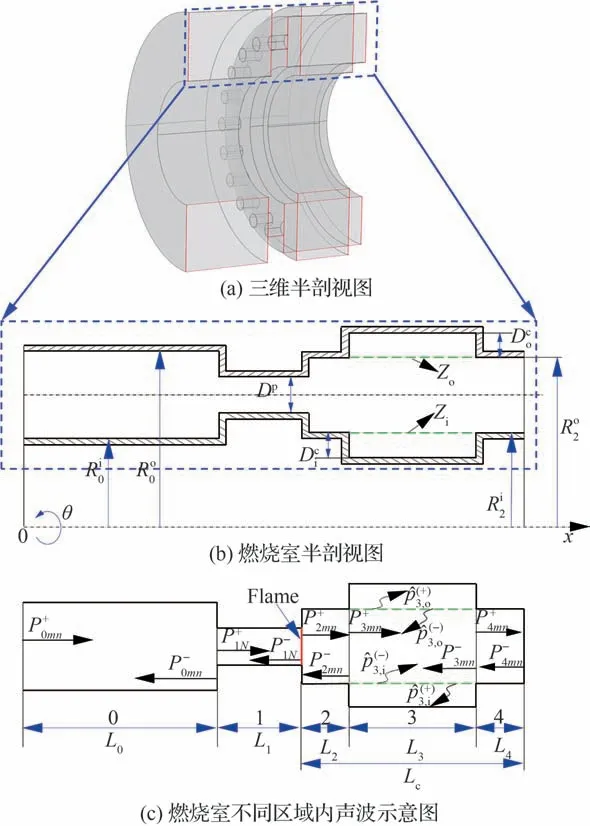
图14 简化环形燃烧室示意图[70]Fig.14 Schematic diagram of simplified premixed annular combustor[70]
为了区分不同部件内的声波,分别用“0”“1”“2”“3”和“4”表示进气前腔,旋流器,燃烧室腔体内声衬前硬壁面部分,声衬部分及燃烧室腔体内声衬后硬壁面部分。为了建立三维模型,需要得到各个部分的声波描述。旋流器足够细,其中的声波可以假设为平面波,进气前腔内声波和燃烧室腔体内硬壁面部分内声波均有关于模态系数的显式解析形式,这里的难点在于如何得到声衬部分即“3”内声波关于和的显式表达式。
Sun 等[71]在发展声衬段声传播模型时建立了传递单元方法,该方法利用等价分布源思想,将声衬壁面视为等价连续分布的单极子声源,从而根据广义格林函数方法,可通过界面匹配条件及穿孔板阻抗方程得到声衬段内声波的关于界面模态系数的显式形式,避免了声衬段内的复杂特征值迭代求解问题,保证了管道特征函数的正交性,便于声传播的计算。传递单元方法将声衬的影响通过传递矩阵的形式将声衬段作为声学单元和硬壁面部分匹配联系,形成特征值问题,将声衬对系统稳定性的影响耦合考虑进来。Li等[68]将该方法用于研究穿孔板声衬对旋流火焰燃烧不稳定性控制效果。Zhang 等[72]研究了一种纯抗性膜结构声衬对Rijke 管热声不稳定性的控制效果。Qin 等[73]基于三维模型方法研究了考虑非线性火焰描述函数情况下,声衬对纵向不稳定模态的控制效果。考虑更复杂的几何及多声衬布置的环形燃烧室构型[74],声衬段内的声波需要考虑内外环壁面声衬散射声波的影响。根据等价分布源思想,声衬段内声波扰动量可以写为硬壁面边界条件下的入射声波和内外环声衬散射声波之和:
式中:r=(x,θ,r)。
声衬在燃烧室腔体内的散射声波p̂(-)3为内外环声衬散射声波之和:
声衬在主管道内散射声波和其在声衬背腔内的散射声波可以通过格林函数得到
外环、内环穿孔板处的阻抗方程分别为
式中:Zo,i为外环或内环穿孔板声阻抗值为外环或内环穿孔板表面等价声质点速度垂直分量。阻抗可以通过适合燃烧室壁面的阻抗模型建立得到,如考虑偏流和切线流干涉及小孔厚度的阻抗模型[75-77]。通过对式(18)和式(19)进行正弦变换,可以求得,将之代入式(16)和式(17)中,可得到声衬段内的声波关于模态系数的显式形式:
根据硬壁面的声波形式,界面守恒匹配条件及火焰传递函数可以形成特征值问题研究穿孔板声衬对燃烧室不同燃烧不稳定性模态的控制效果。Zhang 等[74]根据三维燃烧不稳定性模型研究了内外环声衬布置对环形燃烧室轴向及周向模态的控制效果,如图15[74]所示。

图15 COMSOL 和本三维模型在不同的径向耦合模态数下计算得到的系统复特征频率随声衬长度的变化对比[74]Fig.15 Comparison of variation of complex eigenfrequencies with length of liner obtained by COMSOL and our 3D model under different radial truncated mode numbers [74]
图15 展示了本三维模型与COMSOL 计算得到的考虑内外环声衬时,环形燃烧室不同模态的复特征频率,图中,L 表示纵向模态,A 表示周向模态。1L0A、2L0A 及0L1A 分别表示一阶纵向模态,二阶纵向模态及一阶周向模态。Nt表示三维模型中考虑的耦合径向模态数。当只考虑第一阶径向模态(Nt=1)时,模型退化为二维模型,系统的复特征频率随声衬长度变化的大致趋势能得到,但当声衬控制效果显著时,也即是在系统增长率较低范围内,只考虑第一阶径向模态所预测的结果会有偏差。以模态2L0A 为例,当声衬长度在L3/Lc∈(0.13,0.73)时,只考虑第一阶径向模态会导致预测的增长率比考虑更多耦合径向模态预测增长率偏高,也就是说,此时模型预测会低估声衬的控制效果。从模态形状的比较可以看出[74],只考虑第一阶径向模态不能准确地预测系统内的声模态分布,特别是捕捉不到声衬段附近高阶模态的影响作用。还可以观察到,该声衬对模态2L0A 相比于模态1L0A 和0L1A 的影响作用更大。
当考虑非定常热释放时,研究发现,系统的复特征频率随声衬长度变化的规律与不考虑非定常热释放情况下系统复特征频率的变化规律类似,如图16[74]所示。不过,区别在于考虑非定常热释放后,考虑径向模态耦合对于准确预测系统的特征频率更为重要,特别是对于模态1L0A和0L1A。这一点可以通过比较图15 和图16 发现。实际上,忽略径向模态耦合,会导致系统内声压分布预测不准确,当不考虑非定常热释放时,这只会导致声衬耗散能力预测不准;而考虑了非定常热释放后,它不仅会导致声衬耗散能力预测不准,还会导致热声不稳定性发生的驱动力,即火焰面处非定常热释放和声波的热声耦合的不准确。
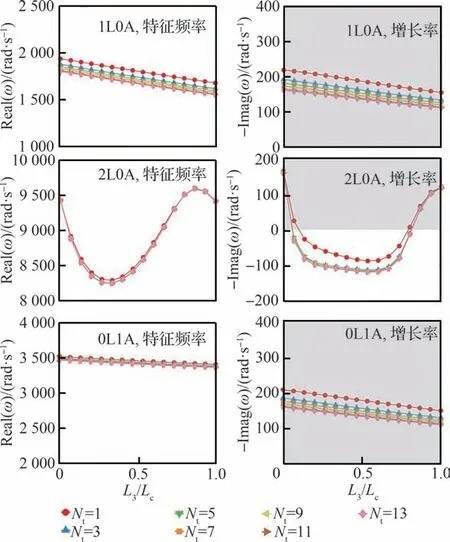
图16 考虑非定常热释放时本三维模型在不同的径向耦合模态数下计算得到的系统复特征频率随声衬长度的变化[74]Fig.16 Variation of complex eigenfrequencies with length of liner obtained by our 3D model under different radial truncated mode numbers with unsteady heat release rate [74]
此外,通过对内外环声衬控制效果的比较发现,对于多声衬控制的燃烧室系统,在燃烧室增加布置声衬不一定会得到正的控制收益,因此,需要耦合考虑多声衬的综合控制效果,因为任一引入的声软壁面都会改变系统的声模态分布,进而影响其余声衬的控制效果,以及所有声衬的综合控制效果。
另外,发现对于纵向模态,声衬布置在燃烧室进口处控制效果最好,该位置对应于纵向模态的压力波峰位置。而当其布置在压力波节处,控制效果不好。通过分析声衬穿孔板两侧声模态分布可知,当声衬位于波峰位置处时,穿孔板两侧总的声压差异较大,引起的声耗散也最大,如图17[74]所示。反之,当声衬位于压力波节处时,则没有足够多的声压差异发挥声耗散作用,如图18[74]所示。这也是在加力燃烧室设计防振屏时,通常将防振屏布置在燃烧火焰区域的原因。
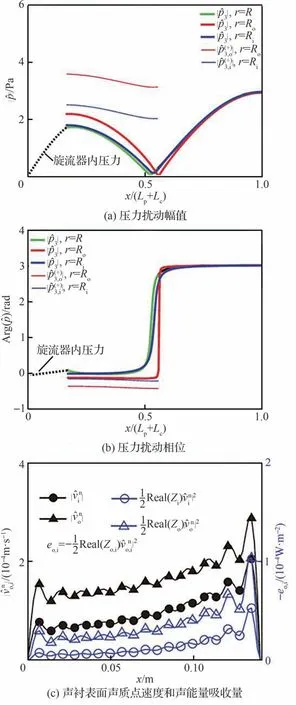
图17 模态2L0A 形状(L2/Lc=0, L3/Lc=0.47)[74]Fig.17 Mode shapes for Mode 2L0A(L2/Lc=0,L3/Lc=0.47)[74]
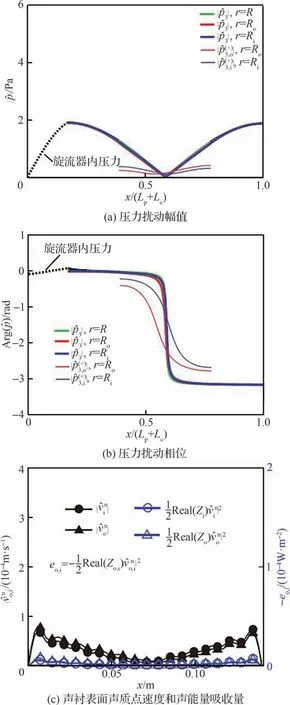
图18 模态2L0A 形状(L2/Lc=0.26, L3/Lc=0.47)[74]Fig.18 Mode shapes for Mode 2L0A (L2/Lc=0.26,L3/Lc=0.47)[74]
特别地,通过观察周向模态,发现周向均匀声衬对周向模态控制效果不好。同样地,该现象可以从周向模态分布特点来解释这一现象,为了更好地控制周向模态,可以采用周向非均匀声衬来进行控制,为此,需要发展能够考虑周向非均匀声衬的声学模型以及燃烧不稳定性分析模型。
综上所述,燃烧室壁面通有冷气的开孔结构不仅起到冷却燃烧室壁面免于烧蚀的作用,同时起到增加系统声学耗散的作用。实际燃烧室内的开孔设计不仅需要考虑高效冷却,还要借助三维燃烧不稳定性模型对多声衬的热声控制效果进行优化。
3.2 非均匀穿孔板声衬控制效果
发展非均匀声衬新型控制方法,旨在弥补均匀声衬对周向不稳定模态控制能力的不足。为此,可以在2 个方面提升对周向不稳定模态的抑制效果:① 在周向均匀声衬背腔内增加轴向安装的硬壁面隔板,从而可以改变背腔内声模态分布,影响声衬的控制效果;② 在旋流器出口(燃烧室进口)安装面设置非均匀穿孔结构,以增加对周向模态的耗散。前者模型的建立需要在3.1 节的基础上,增加对周向分段声衬段内声波描述模型[70]。后者模型的建立,则需要将安装面上的非均匀分布壁面视为“等效源”,利用格林函数方法建立匹配方程,形成特征值问题。对于包含周向非均匀分段声衬的燃烧不稳定性分析模型,壁面声衬的周向非均匀性,会引起周向模态的耦合,声衬表面的等价声质点速度需要在轴向和周向2 个方向进行展开:
穿孔板处的阻抗匹配方程需要在周向分段进行:
式中:P为背腔内隔板总数;θN为第N个隔板角度。另外,建立环形扇形封闭背腔的格林函数为
式中:θ'和r'分别表示声源周向坐标和径向坐标。对式(23)和式(24)采用正弦积分变换,可以求得内外环穿孔板处等价分布声质点速度,代入声衬段内声扰动方程,可以得到声衬段内声扰动关于入射模态系数的显式形式为
同样地,结合界面匹配条件及火焰传递函数,可以建立起包含周向非均匀分段声衬的三维燃烧不稳定性预测模型[70]。该模型可以考虑背腔内任意角度插入若干数量的硬壁面隔板,以及被隔板分开的每部分扇形穿孔板取不同穿孔参数的非均匀性。
图19[70]给出了在考虑周向分为2 段声衬,即在背腔内120°和240°处插入2 个硬壁面隔板,系统的特征模态频率及增长率随声衬长度的变化情况。图中比较结果可以验证本模型方法的有效性。另外,非均匀声衬的引入使得每个退化的(Degenerate)周向模态分裂为2 个周向模态,分别用“+”和“-”表示2 个模态分支。这正是由于声衬壁面的非对称性,引起的系统模态的对称破缺问题。可以看出,随着声衬长度的增加,2 个分支的频率及增长率差异越大。
通过对比均匀声衬和周向分段非均匀声衬(周向分为2 段,角度分别为120°和240°,及周向分为3 段,角度分别为120°)的复特征频率,如图20[70]所示,相比于均匀声衬,安装分段声衬情况下的增长率要更小,说明周向分段声衬提高了系统的声学耗散,增强了燃烧稳定性。

图20 周向均匀声衬和周向分段声衬条件下系统的复特征频率随声衬长度的变化对比[70]Fig.20 Comparison of variation of complex eigenfrequencies with length of liner for circumferential uniform liner and segmented liners[70]
为了进一步阐释周向分段声衬的作用机制,给出周向均匀(图21[70])以及周向分段声衬(图22[70]和图23[70])的声模态分布情况,展示的周向声模态默认轴向位置为x=L0+L1+L2+L3/2。通过对比可以发现,当燃烧室内布置周向均匀声衬时,由于背腔具有和燃烧室接近相同的周向尺度,背腔内和燃烧室腔体内的周向声模态相似,内外环穿孔板处几乎没有驱动声耗散产生的声压差,因此周向均匀声衬对该周向模态的抑制效果较差。

图21 周向均匀声衬下内外穿孔板两侧模态1L1A 声模态分布及声能量吸收流量[70]Fig.21 Pressure mode shapes of Mode 1L1A at default cutting plane and acoustic absorption of perforated plates for circumferential uniform liner case[70]
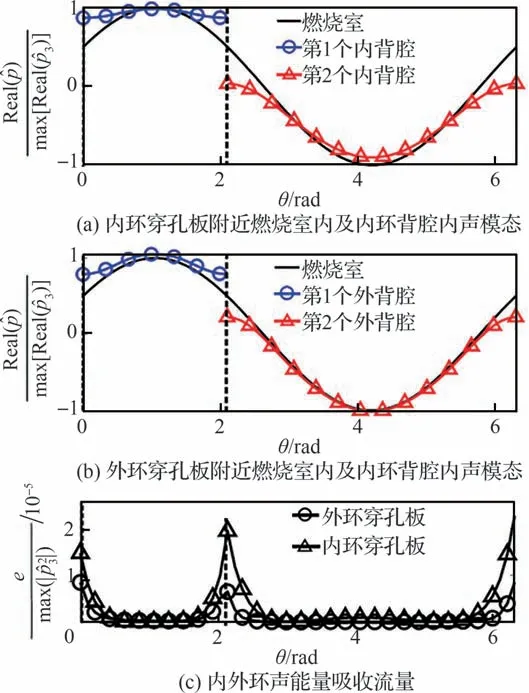
图22 周向分段声衬下内外穿孔板两侧模态1L1A+声模态分布及声能量吸收流量[70]Fig.22 Pressure mode shapes of Mode 1L1A+ at default cutting plane and acoustic absorption of perforated plates for circumferential segmented liners case[70]

图23 周向分段声衬下内外穿孔板两侧模态1L1A-声模态分布及声能量吸收流量[70]Fig.23 Pressure mode shapes of Mode 1L1A- at default cutting plane and acoustic absorption of perforated plates for circumferential segmented liners case[70]
当声衬背腔被隔板分隔形成周向非均匀声衬时,背腔的引入位置在局部形成周向硬壁面条件,进而改变了声衬背腔内的声模态分布,造成穿孔板两侧的声压差,提高了内外环声衬对周向模态的声耗散能力。另外,在非均匀声衬情况下,分裂的2 个模态中,1L1A+的稳定性更强,这也是由于两模态不同的压力分布引起的。对于1L1A+,背腔内和燃烧室内压力波峰重合,而对于模态1L1A-,背腔内和燃烧室内的压力波节重合。
从上面结果可看出周向非均匀声衬引起对称破缺问题,均匀声衬壁面下退化模态分裂为2 个模态,在实际应用中,需要保证每个模态都得到较好控制,才能实现对该阶模态的抑制。
图24[70]展示了不同周向分段声衬结构,结构名中,P 表示隔板,后面数字表示隔板数目,S 表示隔板周向对称分布,A 表示隔板周向非对称分布。通过比较复特征频率结果发现,如图25[70]所示,周向对称的分段(隔板数目>2)声衬,得到的2 个模态仍然是退化的,且具有相同的增长率。P2S 声衬的对称性,不足以使得周向一阶模态退化[70]。对于相同数目的隔板,对称情况下的2 个相同的增长率正好位于非对称情况下的两增长率之间。这个结果表明,对于实际应用的分段声衬,均匀分段声衬能够保证同阶周向模态均得到抑制。

图24 分段声衬结构示意图(阴影部分表示扇形分段背腔,短实线表示背腔内隔板)[70]Fig.24 Configurations of segmented liners (shaded regions denote sector backing cavity and short line segments denote rigid plates)[70]

图25 不同分段声衬下模态1L1A+和1L1A-的复特征频率[70]Fig.25 Complex eigenfrequencies of Modes 1L1A+and 1L1A- for different liner configurations[70]
为了验证周向分段声衬对周向不稳定模态的抑制效果,将火焰非定常热释放包含进来,均匀声衬和周向分段声衬情况下系统的复特征频率结果如图26[70]所示。可以发现,2 种周向分段声衬相比于周向均匀声衬提高了对周向不稳定模态的控制效果。当声衬长度完全覆盖燃烧室腔体时,布置周向均匀声衬的环形燃烧室仍是不稳定的,而布置P3S 结构分段声衬燃烧室的周向不稳定模态得到了完全抑制。布置P2A 结构分段声衬的其中一个模态分支得到抑制,另一分支虽然相比均匀声衬稳定性有提高,但仍是不稳定的,这也再次说明,实际应用中,为了保证所有同阶的周向模态得到抑制,最好采用周向均匀分段声衬。
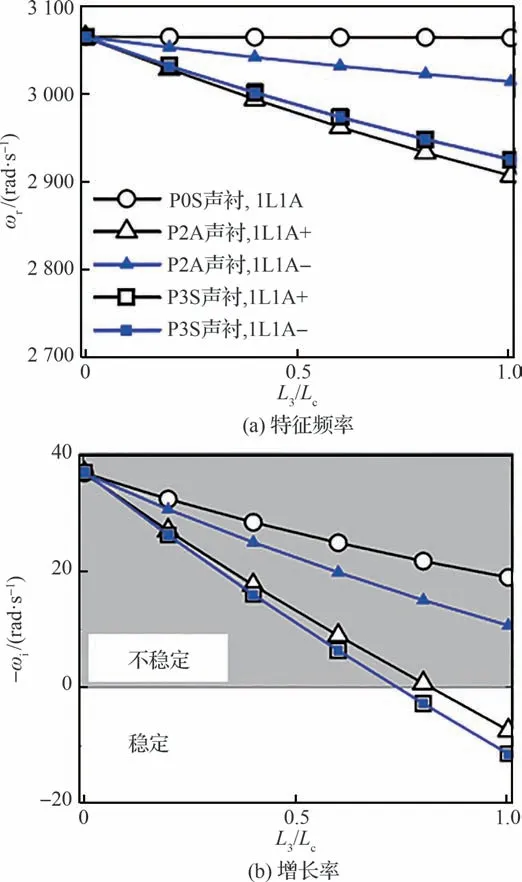
图26 考虑非定常热释放时均匀声衬和周向分段声衬条件下系统的复特征频率结果[70]Fig.26 Results of complex eigenfrequencies for uniform liner and segmented liners with unsteady heat release rate[70]
综上所述,周向非均匀声衬通过改变燃烧室声衬背腔和燃烧室腔体内的模态分布,提高了壁面声衬的控制效果,通过在声衬背腔中增加隔板的方式不会对燃烧室的设计带来较大难度,在工程应用中也更容易实现。
另外,结合数值模型方法,Dai 等[78]研究了不同周向壁面阻抗非均匀分布布局对周向声模态的散射吸声机制。研究结果表明,声衬阻抗周向非均匀布局形式对模态散射具有重要影响,而且周向非均匀阻抗对宽频噪声具有更好的降噪潜力。在后续研究中,可以进一步将壁面阻抗周向非均匀性包含进模型中,基于模态散射机制,进一步优化周向非均匀壁面声衬对周向不稳定模态的抑制效果。
为了突破环形燃烧室壁面声衬抑制能力限制,可以对旋流器出口安装面进行开孔耗散优化设计,如图27[79]所示,进一步提升系统对周向燃烧不稳定性的抑制效果。在燃烧室内外侧壁面为硬壁面的条件下,系统的周向一阶模态复特征频率随安装面穿孔率和小孔偏流的变化情况如图28[79]所示:系统频率随着穿孔率增大而降低,随偏流的增加而增加;在安装面为硬壁面边界时,增长率>0 s-1,系统处于不稳定状态,而安装面穿孔后,存在穿孔率最优值,使周向一阶模态增长率<0 s-1,系统不稳定性得到抑制。这也表明,旋流器出口安装面上引入穿孔耗散,有助于周向燃烧不稳定模态的抑制。

图27 旋流器出口安装面开孔示意图[79]Fig.27 Sketch of perforated injector mounting surface[79]
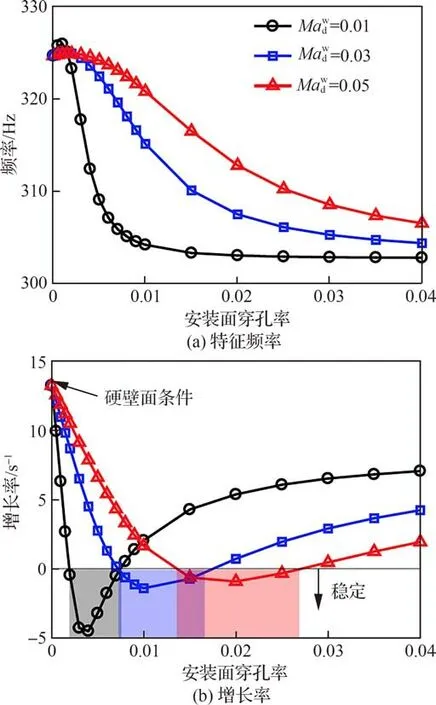
图28 不同安装面偏流条件下系统复特征频率随穿孔率的变化[79]Fig.28 Variation of complex eigenfrequencies with perforation ratio for different bias flow conditions[79]
实际上,Qin 等[79]所发展的理论方法能够实现安装面非均匀开孔的燃烧不稳定性抑制设计。如图29[79]所示,固定内圈穿孔保持不变,变化外圈穿孔参数,包括外圈穿孔率σdo、开孔半径、小孔偏流马赫数,可以研究安装面径向非均匀声衬阻抗分布对周向模态的控制效果。图30[79]结果表明,系统特征频率随孔径和穿孔率增加而减小,而随偏流马赫数的增加而增大。增长率结果表明,外圈穿孔率的增加将显著增大燃烧系统的增长率,在0.001≤σdo≤0.006 时可以保证周向一阶模态的稳定性。 此外,增大偏流和孔径半径也有利于系统稳定性,当>0.02 或>5 mm 时,系统稳定。 图30(b) 表明,在非均匀径向穿孔的情况下,当外圈的> 0.04 时,稳定性得以保持,这与图28(b) 中所示的均匀阻抗的不稳定性形成对比。这有助于扩大取值范围以保证系统的稳定性。
图29 旋流器出口安装面径向非均匀开孔示意图[79]Fig.29 Sketch of nonuniform radial perforated injector mounting surface[79]
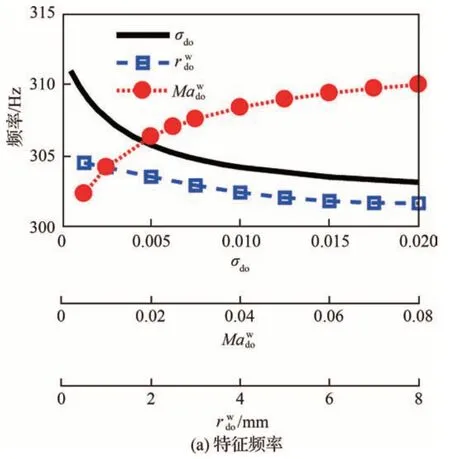
图30 系统复特征频率随穿孔率σdo、开孔半径rdwo 和小孔偏流马赫数 的变化[79]Fig.30 Variation of complex eigenfrequencies with perforation ratio σdo, radius of aperture , and Mach number of mean bias flow
4 总结及展望
随着航空发动机性能的不断提高,航空发动机燃烧不稳定性问题也变得更加复杂且难以解决。燃烧不稳定性问题仍是目前航空发动机领域需要重点研究的关键难题。本文综述了针对航空发动机燃烧不稳定性问题已开展的关键研究成果,包括燃烧室非定常流动及火焰,燃烧不稳定性声网络预测模型及三维燃烧不稳定性预测控制模型等。
1) 加力燃烧室钝体流动受声激励而影响燃烧火焰非定常热释放主要通过K-H 不稳定性及BVK 不稳定性2 种机制进行。进口温度的变化通过影响火焰面前后的密度比影响钝体尾迹非定常流动特征,进而影响火焰非定常热释放。对于新一代航空发动机加力燃烧室,燃烧室的进口流动条件、火焰稳定器形态、燃油喷射方式等变化,均给加力燃烧室燃烧不稳定性耦合发生机理带来新的未知因素,需要开展更深入的试验及理论模型研究。
2) 贫油预混预蒸发旋流火焰广泛应用于民用航空发动机环形燃烧室中。其非定常响应特性受声波直接激励产生的涡脱落对流引起火焰面的卷曲扰动和旋流数扰动引起火焰角度扰动的共同影响。火焰传递函数及描述函数模型的建立,为燃烧不稳定性模型发展提供了基础。然而,面向多火焰耦合干涉问题,多频率、多模态声激励下非线性响应问题,仍需开展更深入的研究。
3) 基于特征值分析的燃烧不稳定性声网络预测模型具有计算快速、物理概念清晰等优势特点,使其在工程设计及学术研究方面均具有较强的适用性,为分析燃烧室不稳定模态及研究影响不稳定模态参数规律提供了理论模型基础。然而,传统的预测模型均建立在硬壁面条件下,不能对声软壁面进行直接耦合设计。
4) 三维燃烧不稳定性预测控制模型,将燃烧室内多声衬壁面耦合考虑进来,能够通过特征值分析对声衬壁面下的系统燃烧不稳定性模态的特征频率及增长率进行预测,并对壁面控制声衬的布局进行优化设计。下一步,需要开展更多包含燃烧室系统复杂边界及热源耦合干涉的研究,并配合更多精细化试验研究,为支撑先进航空发动机燃烧不稳定性问题排故提供理论模型工具基础。
