多级压气机转子负荷系数对叶片非同步振动的影响

程荣辉，余华蔚，汪松柏，杜林，孙大坤，孙晓峰

1．中国航发沈阳发动机研究所，沈阳 110015

2．中国航发四川燃气涡轮研究院，成都 610500

3．北京航空航天大学 流体与声学工程实验室，北京 102206

叶轮机械中，叶片的非同步振动（Non-Synchronous Vibration， NSV）是指叶片振动频率与转子转频不成整数倍关系，非机械振动激励或尾迹周期性激励诱发。广义上，对于压气机叶片非同步振动，根据其气动激励的诱因不同，还可分为叶尖气动旋转不稳定（Rotating Instability，RI）激励振动、失速颤振（Stall Flutter）、声共振［1］等。失速颤振起始阶段，往往伴随叶片振幅的迅速增长，既有可能随着阻尼的增加进入一定振幅的极限环振动状态，也有可能由于应力过大在短时间内出现叶片裂纹。然而压气机总压升对该现象相对不敏感，甚至很难反映出变化，这也是该现象难以监测的原因之一。而叶尖气动旋转不稳定激励共振的特点是叶片不会短时间内失效，压气机出口总压也不会出现类似失速边界的急剧下降，压气机能维持稳定的工作。与颤振现象不同，旋转不稳定现象一般会先出现叶尖附近的非定常压力脉动，即在振动出现以前观察到分离脱落涡，脱落涡在转子叶片上产生非定常气动激励，失速团的模态数和周向传播速度是决定激励频率的关键参数，只有当失速团的激励频率与叶片固有频率相匹配时才易激发出叶片的振动。

叶尖旋转不稳定及其诱发叶片振动的现象，主要发生在发动机非设计工况。当不稳定流体的气流激励频率接近转子叶片固有频率，会导致叶片大幅度振动，极大几率造成叶片高周疲劳失效，甚至在短时间内叶片破坏断裂。国外主要发动机公司（罗·罗、GE、普惠等）在新型发动机研制过程中，均出现了压气机转子叶片非同步振动问题［2-6］，中国在航空发动机研制过程也出现类似问题［7-10］，这也是未来高性能航空发动机研制必将面临的技术挑战。

压气机转子叶片非同步振动是一种机理复杂、产生机制尚不完全清楚的气动弹性现象。目前，国内外针对压气机转子叶片非同步振动的耦合机制尚无统一的结论。 Baumgartner［2］、Im［11-12］、Vo［13］、Kameier［14-15］、Mailach［16-17］等认为旋转不稳定是诱发转子叶片非同步振动的主要原因，旋转不稳定性通常发生在具有大径向间隙的压气机转子高负载工况下，与叶尖不稳定涡的周向运动有关。叶尖不稳定涡的产生除了与转子径向间隙大小直接相关外，还和转子实际工作的级负荷有重要关系，而这方面的研究结果相对较少。帝国理工大学的Lu 等［18-19］认为风扇转子喉道的激波位置振荡对转子叶片非同步振动影响很大，通过降低转子叶尖气动负荷，控制喉道的激波位置振荡区域，可以抑制转子叶片非同步振动的产生。

到目前为止，在非设计工况下，受限于湍流模型和仿真模型几何偏差等因素，CFD 在叶尖不稳定涡的发展演化机制方面的数值仿真不确定性较高，且要反映整个物理过程需要开展全环非定常数值模拟，计算量巨大，尤其是考虑叶片振动以后的流固耦合模拟会进一步增加数值模拟的困难，难以在研究中广泛应用。因此，基于试验研究非同步振动的机理和影响因素，仍然是最有效的技术途径。

本文利用曾出现过非同步振动现象的多级压气机开展试验研究，通过调节导叶/静叶角度改变转子级负荷，重点分析了转子级负荷对压气机叶片非同步振动的影响机理。试验测量的主要手段是在机匣上安装非定常压力脉动测试和同步的转子叶片应变测试，分析二者的频率和模态关系，阐明旋转失稳诱发转子叶片非同步振动这一复杂的物理现象。本文的研究工作分为3 部分，第1 节将基于多级压气机整机试验数据，结合非定常数值计算，分析导叶偏关引起的转子负荷偏高，进而诱发旋转失稳和叶片振动的物理现象。第2 节，为了进一步深入研究叶片负荷对多级压气机旋转失稳现象的产生机理，开展了一系列静子叶片角度的分析，给出了对应的转子负荷随叶片调节角度偏离的变化规律，为进一步的机理试验研究提供了理论指导。根据第2 节的理论预测结果，第3 节针对性地开展了导叶/静叶角度调节试验，详细分析了导叶调节、负荷变化对非定常压力脉动、应变信号的产生关联，探讨了叶片负荷对旋转失稳现象的产生机理。

1 旋转失稳诱发的叶片振动现象及机理

1.1 整机试验多级压气机旋转失稳诱发叶片振动信号分析

本节试验工作在某整机试验台上展开，试验中主要观察到第1 级转子出现异常情况，其转子叶片数为47，叶尖马赫数为1.125，气动弯角为10.2°。试验中，采用了图1 所示的测试布局方案。其中图1（a）给出了叶尖动态压力传感器测点轴向位置的示意图，图1（b）是对应的周向测点位置，3 个测点夹角为20°和40°，用于识别旋转失稳流动结构的频率、模态。本节的整机试验测试中为了避免应变片对性能测试结果的影响，没有布置应变测量。在第3 节的部件测试中，增加了叶片表面的应变测量以分析叶片的振动响应。压气机试验过程中，第1 级转子壁面脉动压力传感器感受的是绝对坐标系下的流场压力激励频率fS，而压气机转子叶片感受的脉动压力是在相对坐标系下进行的，转子叶片感受的扰动频率为fR，因此，只有当fR与转子叶片固有频率接近时，才会引起叶片的强迫振动，而fS与转子叶片固有频率的匹配并不会引起系统的振动。如果转子转频为EO，且转子叶片已经出现振动锁定，脉动激励旋转速度与转速一致，fS和fR满足

式中：m为任意正整数［15］，由转子叶片数和振动节径数共同决定。此时fR为叶片振动频率。

旋转失稳诱发叶片振动的试验结果在国际上报道很少，尤其是多级压气机更为少见，这主要由于其试验测量难度与风险很大。用于本文研究的是一台核心机试验出现的异常结果，核心机降低转速时压气机静叶调节机构出现故障，叶片调节角度异常偏关、各排叶片调节比例失调，导致压气机未按预计工作线降低转速至目标工作点，而是向堵塞边界严重偏移，第1 级转子叶尖对应机匣的壁面动态静压出现脉动幅值突增现象，叶尖动态压力时域脉动幅值从6% 增大至20%（见图2（a）），同时频谱出现一系列非整数倍转频的异常信号，且各异常频率间隔是转频的整数倍。试验后分解检查发现第1 级转子有5 个叶片根部出现裂纹，断口分析起裂原因为高周疲劳。

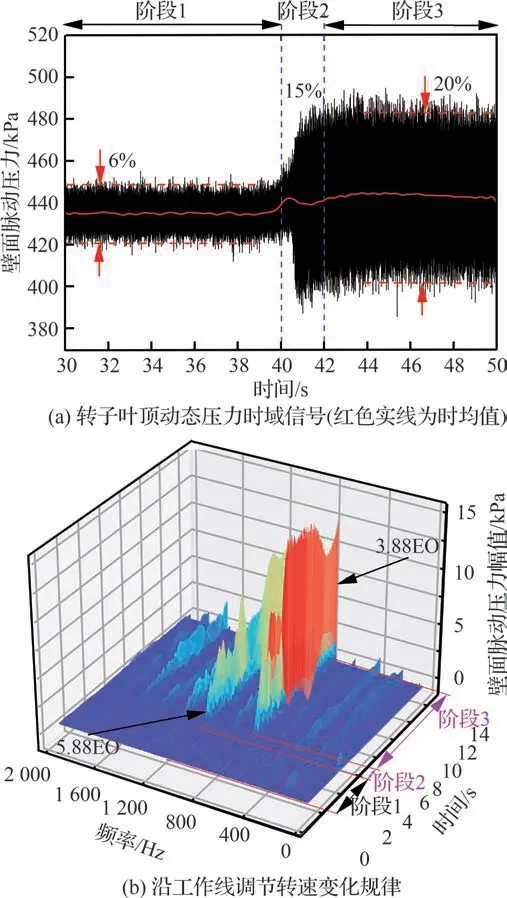
图2 压气机异常脉动压力时域-频域分析Fig.2 Joint time-frequency-amplitude analysis of abnormal pressure fluctuation of compressor

脉动幅值是对试验监测到的原始脉动压力信号直接进行相对峰-峰值计算，计算式为

式中：pmax为最大脉动压力值；pmin为最小脉动压力值；pm为时均脉动压力值。

对第1 级转子叶尖的壁面动态压力进行频谱分析，动态压力时域-频域分析如图2 所示，3 个阶段的典型动态压力频谱分析如图3 所示，阶段1为正常工作阶段，阶段2 第1 级转子叶尖压力脉动的幅值大幅增大，转子叶尖压力时均值也迅速增大（图2（a）中红色线为时均值），表明第1 级转子叶尖的气动负荷急剧增大，此时第1 级转子叶尖流场中的频谱较为丰富，最先突起的是5.88EO，之后为3.88、6.88、7.88、8.88、4.88 倍的EO，且这些频率信号的幅值均大于转频EO 幅值（见图2 和图3）。进入阶段3 后，第1 级转子叶尖脉动压力时均值维持较高的量值且趋于稳定，压力频谱中的5.88EO 幅值迅速下降，而3.88EO幅值迅速增大，而6.88、7.88、8.88、4.88 倍EO的幅值依然较高，比基频及其倍频幅值高得多，同时流场中还能较明显捕捉到0.88EO 和1.88EO的信号。上述脉动压力信号具备2 个特征：① 峰值频率非转频整数倍；② 频率间隔正好为转频。

图3 压气机异常脉动压力频谱分析Fig.3 Spectrum analysis of abnormal pressure fluctuation of compressor

第1 级转子叶片的一弯固有频率为3.88EO，即可根据式（1）对本次试验中捕捉的气流异常脉动信号进行流固耦合的模态分析。阶段1 时压力信号正常，只有转频整数倍的压力尖峰，且都在1 kPa 以下。阶段2 气流脉动时域信号幅值从6%大幅提高至15%左右（见图2（a）），更为重要的是，出现的fS=5.88EO 的脉动尖峰，幅值高达7 kPa 以上，远远高于阶段1（见图2（b））。此时m=2，说明流动激励5.88EO 和叶片的一弯固有频率达到m=2 的耦合，相互激励增大。继续发展到阶段3 时，气流脉动时域信号幅值继续提高至20%（见图2（a）），出现fS=3.88EO，幅值高达16 kPa，已经远远超出常规试验监测脉动压力范围（见图3（c））。此时m=0，说明转子盘的振动节径数发生了变化，流动激励3.88EO 和叶片的一弯固有频率已经完全耦合了，相互激励增大，而转子叶片的振动应力幅值也大幅提高，导致叶片萌生裂纹。

上述试验捕获到非同步振动是在压气机的中高转速，第1 级转子叶片出现的非同步振动正是由于叶尖流场出现旋转不稳定后，流动激励频率与叶片固有频率产生耦合而发生的。需要指出的是，该核心机经过多轮试验，同转速下，当静叶调节角度没有发生偏离、转子负荷正常时，并未观察到类似的压力脉动信号。表明此次试验中的现象并非由于通常认识的单纯叶尖间隙过大引起，而是与导叶异常偏关带来的叶尖负荷过高紧密相关，分析认为转子负荷系数决定了叶背流动的分离程度以及叶尖压差，进而影响了周向流动激励的形成，叶尖泄漏流并非旋转不稳定发生的必要条件，压气机处于非设计状态时，转子负荷系数的变化对非同步振动的影响鲜有报道。为进一步确认以上结论并揭示其物理机制，将开展调节各级静叶角度的多级压气机试验，以探究转子负荷与叶尖旋转失稳结构以及叶片动应力之间的影响规律。

1.2 全环非定常数值模拟对导叶偏关诱发旋转失稳探究

在实际问题中，如何分辨颤振和旋转失稳诱发的振动在实际中是非常困难的问题，二者都具有非同步振动共同具备的特征。为此，本文开展了全环非定常数值模拟探究导叶偏关诱发旋转失稳现象，来帮助分析1.1 节中的工况是否有出现旋转失稳现象的可能。在上述试验中无法定量地获取第1 级静叶实际的偏关量，更无法获得叶尖附近的流场细节。为了定量模拟压气机转子叶片负荷变化对旋转失稳现象产生及叶片气流激励的影响。考虑整个压气机部件多级非定常数值计算量规模超大，本文计算模型选取压气机前1.5 级，如图4 所示。采用H-O 型结构化网格，无量纲参数Y+为20～30，全环模型网格总节点数约为4 200 万，如图5 所示。湍流模型采用k-ε模型，非定常时间步长为4.17×10-6s。非定常数值计算流量的收敛情况如图6 所示。

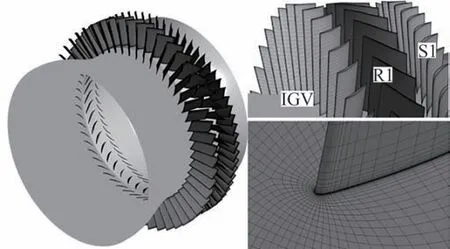
图4 非定常数值模拟全环模型Fig.4 Full-annulus unsteady numerical simulation model

图5 非定常数值模拟网格Fig.5 Mesh of unsteady numerical simulation

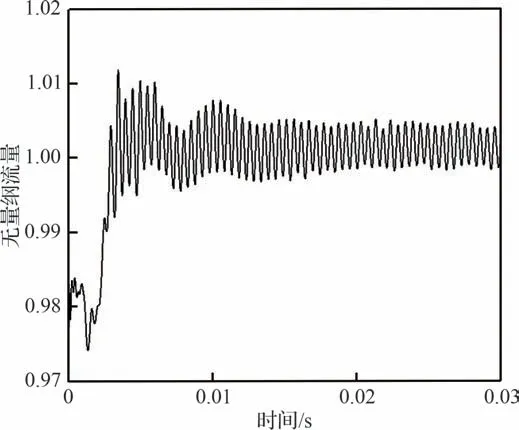
图6 非定常数值计算收敛情况（进口流量）Fig.6 Convergence of unsteady numerical simulation（inlet mass flow）

为了探究第1 级转子叶尖负荷增大的影响，在保持进出口静压不变的前提下，模拟第1 级静叶在3 种设计调节角度基础上偏关角度2°、4°、6°下的非定常流动引起的压力脉动。仿真计算中在第1 级转子叶片90%叶高前缘设置监测点，图7 为第1 级静叶3 种偏关角度下第1 级转子叶尖的压力脉动时域信号，可见第1 级可调静叶偏关使得压气机转子叶片表面非定常压力脉动幅值增大。偏关2°时，转子压力脉动幅值（式（2）定义的峰-峰值脉动幅值）为1%左右；随静叶偏关量增大至4°，脉动幅值增大到2%左右；当偏关角度增大至6°时，压力脉动幅值可达6%，且波动较大。可知随第1 级转子叶尖负荷的增大，叶尖压力脉动幅值逐渐增加，表明转子不稳定流动加剧，转子叶尖流场逐渐恶化。

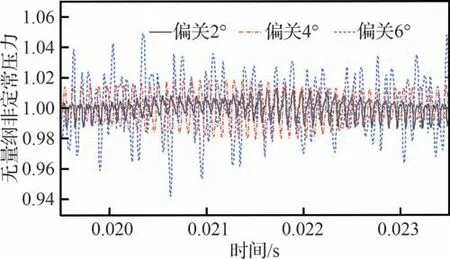
图7 第1 级转子90%叶高前缘监测点压力脉动随静叶偏关角度变化Fig.7 Variation of pressure fluctuation at leading edge monitoring points of 90% span on the first-stage rotor with closing angle of stator

对于气弹现象更为重要的是气动激励的频率，图8 为第1 级静叶不同偏关角度下转子叶片上由于旋转失稳流动引起的气动激励力对比，通过叶片表面两侧的压力积分获得，其中F为瞬时值，Fˉ为时均值。从图中可以看出，第1 级静叶偏关2°时流场的气流激励频率为叶片的1 倍通过频率（1BPF），没有发现非同步气流激励频率。在低于叶片1BPF 的频率带内，导叶偏关4°和6°均导致转子出现非同步气流激励频率（1.9EO，根据式（1），可以计算得到对应的旋转失稳模态数为23），且偏关6°时非同步气流激励频率幅值相对偏关4°增大了67%左右。该非整阶次激励产生的气动力幅值远高于在52EO 处由于IGV 尾迹激励产生的非定常力。可知当第1 级静叶偏关较多导致第1 级转子叶尖负荷增大时，周向不稳定气流使得转子出现非同步气流激励频率，非同步气流激励幅值随转子负荷增加而急剧增大。图9 为第1 级静叶不同偏关角度下叶尖非定常流场，静叶偏关角度增加使得转子叶尖负荷增重、流场恶化，叶背侧出现气流分离现象。图10 为静叶偏关6°时的叶尖分离涡与间隙泄漏流，图11 为静叶偏关6°时的转子出口相对马赫数周向分布，可见其相互作用卷起的“龙卷涡”，使得叶尖流动不稳定，是导致转子出现非同步气流激励的主要原因。这也表明转子叶片尖部负荷增大与大间隙叶尖泄漏流动同样能引起叶尖流动不稳定，导致出现非同步气流激励。

图8 第1 级静叶不同偏关角度下由于旋转失稳流动引起的气动激励力对比Fig.8 Comparison of unsteady forces induced by RI flow structure at different closing angles on the first-stage stator

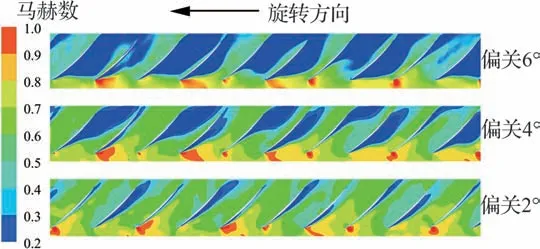
图9 第1 级静叶不同偏关角度下转子叶尖流场对比Fig.9 Comparison of rotor blade tip flow field with different closing angles on the first-stage stator

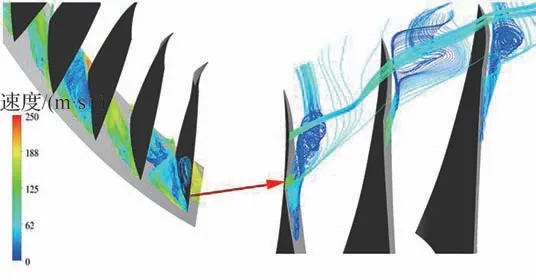
图10 转子叶尖分离涡与间隙泄漏流相互作用（偏关6°）Fig.10 Interaction of rotor blade tip separation vortex with leakage flow （close stator by 6°）

图11 转子出口相对马赫数周向分布（偏关6°）Fig.11 Circumferential distribution of relative Mach number at outlet of rotor （close stator by 6°）

2 多级压气机转子叶尖负荷系数计算

1.2节所述1.5 级压气机全环非定常计算初步解释了调节叶片角度偏关对相邻上游转子旋转失稳现象的影响机理，然而其计算量对于多级压气机非定常模拟是难以接受的。为研究在更为复杂的多级压气机环境下导叶/静叶角度对旋转失稳现象的影响规律，开展6 级压气机部件试验研究。为了给试验研究提供理论支持，采用二维（轴对称）数学模型、应用流线曲率法，定量分析不同导叶/静叶偏转角度下，多级压气机负荷系数随转速的变化规律。

本文研究的6 级跨声压气机第1 级转子的叶片数、叶尖马赫数和气动弯角等设计参数与1.1 节中的参数完全一致，但进气条件为常温常压。包括进口导叶和第1、第2 级静子叶片共3排可调叶片。为指导试验调试策略，获得6 级压气机各级级负荷随导叶/静子叶片调节的变化规律，本文采用文献［20］研究的一种工程实用的轴流压气机特性二维预估方法，包含二维（轴对称）数学模型、应用流线曲率法求解完全径向平衡方程来得到压气机内部流场，计算站设在叶片排轴向间隙中，用堵塞系数来考虑环壁附面层的堵塞影响，采用了较精准的叶片排的损失和落后角模型，能真实地反映各种工况下压气机的特性和内部流场，可用于多级轴流压气机的特性计算，已在技术研究和产品研制中广泛使用。

2.1 落后角和损失模型

为能够比较真实地反映多级轴流压气机内部的流动，获得转子负荷系数随导叶/静叶调节角度的变化规律，本文采用了文献［20］建立的落后角和损失模型。落后角的计算公式为

式中：δmin为最小损失落后角；δi为攻角偏离最小损失攻角时的落后角修正；δVA为流管面积变化对落后角的修正；δMa为马赫数对落后角的修正；δn为叶型过扭对落后角的修正；δk为径向间隙对落后角的修正。

损失模型为

式中：ωmin为叶型最小损失；ωM为激波损失；ωt为端区损失；ωk径向间隙造成的损失；i为当前攻角；im为最小损失攻角；iw为可用攻角范围的一半。

2.2 负荷系数计算结果

压气机气动设计中一般常用无量纲性能参数——负荷系数ψ*（Loading Coefficient）来衡量各级负荷。负荷系数又称载荷系数、加功因子，它的定义为

式中：L为有效加功量；U为切线速度。

当3 排可调叶片在设计角度时，通过二维流场计算，获取在压气机工作点和近喘振边界点（近喘点）的第1 级转子叶片叶尖的负荷系数随转速的变化趋势，如图12 所示。当压气机工作状态沿发动机工作线从1.0 设计转速逐渐降低转速时，第1 级转子叶片叶尖的负荷系数随转速的降低变化比较平稳（图12（a）），而沿近喘点，其负荷系数随转速降低呈现出明显的增长趋势（图12（b））。如图13 所示，在近喘点，下游静叶角度偏关，会使第1 级转子叶片的负荷增大，负荷系数也明显提高；下游静叶角度偏开，使第1级转子叶片的负荷降低，负荷系数也明显降低。说明本文1.1 节压气机试验过程中由于调节机构故障导致下游叶片偏关增大了第1 级转子叶片叶尖负荷，使之更容易发生流动不稳定，进而引发旋转不稳定现象。据此结果可以判断：通过打开下游叶片的措施可降低该处负荷，可降低第1 级转子叶片叶尖负荷，避免出现非同步振动。

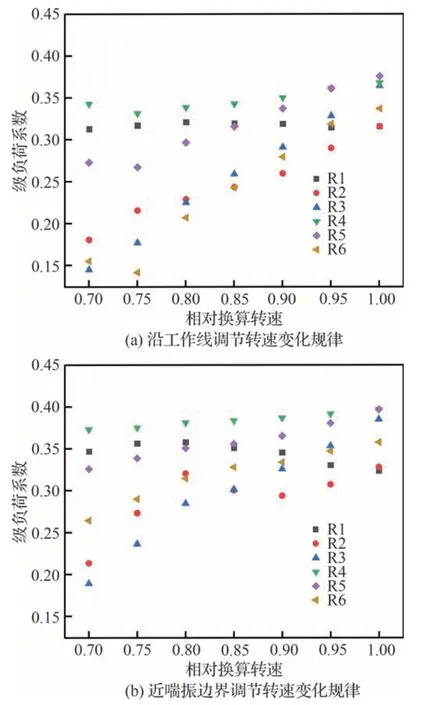
图12 各排转子叶尖的负荷系数随转速变化的计算结果Fig.12 Computed results of change of loading coefficient of each rotor blade tip with rotation speed

图13 近喘边界下游静叶偏开/偏关对第1 级转子叶尖负荷系数的影响Fig.13 Effect of downstream stator open/close on the first-stage rotor blade tip loading coefficient near surge boundary

3 试验研究

本节开展了6 级压气机部件试验，定量调节可调叶片角度，改变第1 级转子叶片负荷，研究多级压气机负荷系数对非同步振动的影响规律。基于第2 节的多级压气机负荷分析，针对增大转子叶尖负荷设计了多个试验方案，一方面获取第1 级转子叶片的负荷对叶片非同步振动的影响情况，另一方面研究对第1 级转子叶片非同步振动影响最敏感的叶片排。需要指出的是本节试验与第1 节中的试验进气条件、物理转速不同，因而各阶叶片固有频率相对转频倍数也不同。

3.1 试验装置及测试方案

本试验在敞开节流式轴流压气机试验器上开展。在压气机进、出口和各级间布置多支多点总温、总压测点，以获取压气机总性能和各级级性能；在压气机进出口布置了动态压力测点，以监测压气机中的异常流动引起的压力变化情况，可达到快速退喘或其他异常状态的目的。本次试验还增加了第1 级转子叶片叶尖的动态壁面静压Ps-R1 监测，以采集第1 级转子叶尖出现旋转不稳定时的气流脉动压力信号。试验中在第1 级转子叶片叶尖对应机匣布置周向3 点动态壁面静压测点：Ps-R1-1、Ps-R1-2、Ps-R1-3，如图1 所示，可见3 个测点夹角为20°和40°，这样布置的目的是为了识别更多旋转失稳模态。传感器采用齐平壁面安装方式，传感器为Kulite XTEH-10L-190M 系列压阻式动态压力传感器，采样率≥20 kHz，带宽≥10 kHz。

根据式（1），机匣布置的动态静压测点获取的是绝对坐标系下的气流脉动频率fS，而还需同步获取叶片振动频率fR，因此试验中在第1 级转子叶片（共47 片）的其中9 个叶片上各布置一点振动应力监测点，位置见图1（c）。图中测点A 主要监测1 阶振动（一弯）、测点B 监测2 阶振动（一扭），测点C 监测3 阶振动（一阶弦弯），将转子叶片上的应变测量与机匣上的动态压力测量同步分析，来研究旋转失稳诱发叶片振动现象。本文中应变信号编号如“R1-3-B”，“R1”代表第1 级转子，“3”代表叶片编号（测试中在若干转子上布置了同样的A、B、C 测点），“B”代表测点位置。试验在相对换算转速为90%时进行。

3.2 上游导叶出口气流角的影响

在压气机试验中，单独调节进口导叶（IGV）安装角，在各级间设置总压监测，获取了各级级压比随IGV 角度偏开（+）和偏关（-）的变化规律，如图14 所示，图中数值表示角度值。可见当IGV 逐渐偏开时，第1 级压比逐渐增大，负荷逐渐增大，而后5 级的压比变化很小。原因是IGV 打开时，第1 级转子叶片进口预旋降低，导致负荷增大。试验中气流脉动压力监测和叶片振动应力监测正常，没有出现异常信号。

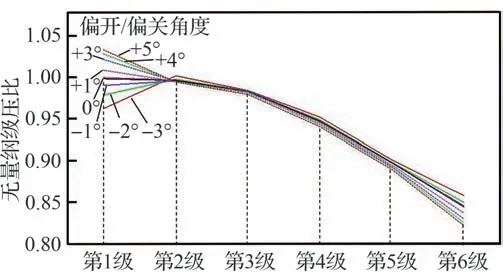
图14 IGV 偏开/偏关对各级压比的影响Fig.14 Effect of IGV open/close on pressure ratio of each stage

3.3 下游静子偏关的影响

试验通过单独偏关第1 级静子叶片S1、第2级静子叶片S2 和同时偏关S1 和S2，定量研究偏关S1 和S2 时，第1 级转子的气动负荷增大的规律。

3.3.1 单独偏关第1 级静叶S1

保持IGV 和S2 设计安装角不变，在相对换算转速为90%时，逐渐偏关（-）S1，此时第1 级转子叶片压比逐渐提高，第2 级压比逐渐下降，后4 级压比变化不大，如图15 所示。

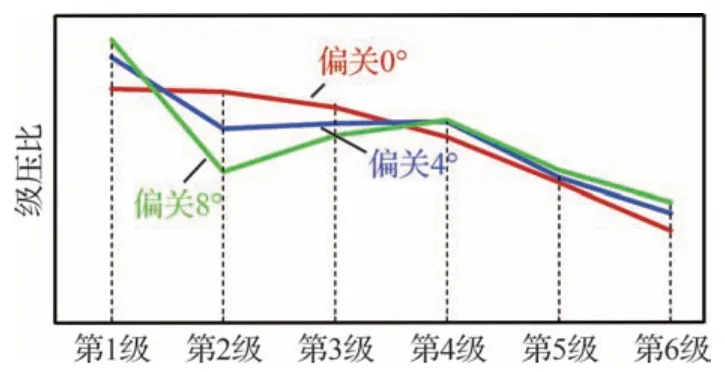
图15 偏关S1 对各级压比的影响Fig.15 Effect of closing S1 on pressure ratio of each stage

在S1 从设计安装角偏关4°～8°的过程中，R1处的机匣壁面动态压力传感器首先出现压力脉动幅值增大，各测点频率成分增加，出现丰富的非整数倍气流激励频谱，以7.16EO 幅值最大，脉动幅值约为2.6%，此时压气机工作稳定，转子叶片振动应力明显增大。当S1 偏关至8°时，壁面动态压力幅值进一步增加，频谱中5.16EO 的幅值最高，同时第1 级转子叶片的振动应力突增，应变片振动应力超限，频率为叶片一弯频率4.16EO。叶片振动应力和气流脉动压力见图16 和图17（图17 中壁面脉动压力强度系数为测量点的脉动压力幅值与进口来流压力脉动幅值均方根的比值），将过程分为以下3 个阶段：

图16 第1 级转子叶片动应力时域图Fig.16 Time-domain vibration stress of the first-stage rotor blade

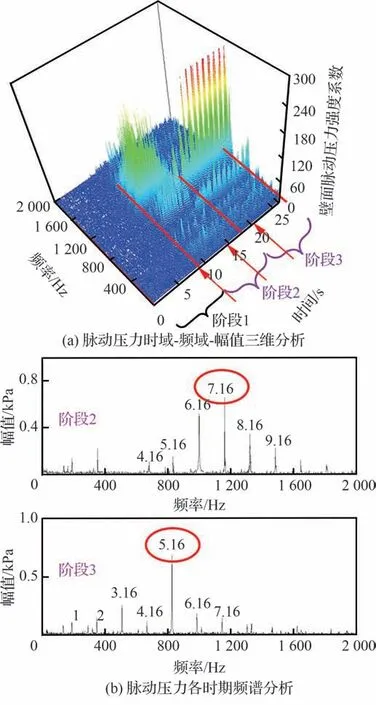
图17 第1 级转子叶片叶尖脉动压力Fig.17 Blade tip pressure fluctuation of the first-stage rotor blade

阶段1偏关4°～8°过程中，该区域内扰动较弱且较为稳定，气流脉动压力的脉动幅值约为2.6%。

阶段2偏关稳定在8°时，该区域为气动扰动与叶片振动耦合作用区域，脉动压力的脉动幅值由4.78%突增至18.58%，同时叶片振动与流场耦合频率较不稳定，叶片的振动应力急剧增加。气流脉动频率fS=7.16EO，叶片振动频率fR=4.16EO，由式（1）可知m=7.16-4.16=3，说明流场中的分离流扰动已经与叶片一弯固有频率产生耦合。

阶段3迅速打开压气机出口节气门，气流脉动压力的脉动幅值略有下降，但整体平均的脉动幅值依然保持在约15.93%的高水平区间，叶片振动处于高应力水平。气流脉动频率fS=5.16EO 频率，叶片振动频率fR=4.16EO，由式（1）可知m=5.16-4.16=1，说明流场中的分离流扰动增大，与叶片一弯固有频率的耦合加深，相互的激励也进一步增强。随着节气门继续打开并降低转速、恢复S1 叶片安装角到设计位置后该异常信号均消失。

3.3.2 单独偏关第2 级静叶S2

在相对换算转速为90%时，保持IGV 和S1设计安装角度不变，研究S2 设计安装角从偏关8°调节至偏开8°对R1 气动性能、振动性能的影响情况。试验结果表明当S2 偏开（+）时，第3 级压比显著提高，第2 级压比显著下降，而S2 偏关（-）时，压比趋势相反，如图18 所示。整个试验过程中，压气机工作稳定，机匣振动、气流压力脉动、叶片振动应力等信号均无异常，当S2 调节至偏关最大8°时，第1 级转子叶片叶尖流场中没有出现异常的压力脉动频率，叶片振动应力也没有增大趋势。

图18 偏开/偏关S2 对各级压比的影响Fig.18 Effect of opening/closing S2 on pressure ratio of each stage

3.3.3 同时偏关第1 级静叶S1 和第2 级静叶S2

相对换算转速为90%时，保持IGV 设计安装角不变，同时偏关S1 和S2 叶片至4°、3.6°时，压气机流量-压比特性如图19 所示。R1 叶尖的气流脉动压力和叶片振动压力时域图如图20 所示，可见随着R1 的负荷逐渐加重，尖部气流脉动幅值有所增大。在阶段1，压比已经快接近喘点压比，该阶段机匣监测到气流脉动出现fS=33.7EO 的频率（模态数m= 33.7+4.3= 38），脉动幅值从3%增大至5.3%，叶片振动应力也从35 MPa 逐渐增大至100 MPa。阶段2 继续关闭节气门，增大R1 负荷，从图20 中可见，气流脉动频率fS=33.7EO，频率幅值略有增大，但突然增加的fS=6.3EO，其频率（模态数m=6.3-4.3=2）幅值更大，导致脉动幅值从5.3%迅速增大至9.3%，同时叶片振动应力从100 MPa 提高到198 MPa，超限报警，台架降低转速停车。

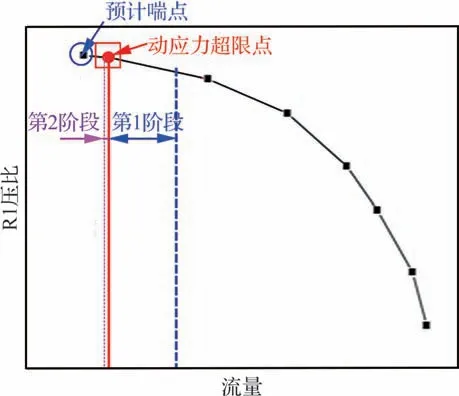
图19 相对换算转速为90%时的流量-压比试验特性Fig.19 Experimental characteristics of mass flow and pressure ratio under 90% relative corrected rotation speed

图20 第1 级转子叶片的气流脉动压力和叶片振动应力Fig.20 Flow pressure fluctuation and blade vibration stress of the first-stage rotor blades

4 结 论

本文开展了理论与试验相结合的研究，通过全环非定常数值计算解释了核心机试验中调节叶片异常偏关引起的转子负荷增加，进而诱发旋转失稳流动与气动脉动激励的物理机制，分析了旋转失稳的流动结构及频率特征；通过6 级压气机二维通流计算分析，给出了不同导叶/静叶角度下，第1 级转子负荷随转速的变化规律；通过6级压气机试验研究，获取了导叶/静叶角度对转子负荷的影响规律，揭示了旋转失稳诱发叶片振动的物理现象，主要结论如下：

1） 除叶尖径向间隙大外，转子叶尖高负荷是产生旋转失稳流动现象，诱发转子叶片非同步振动的重要原因。

2） 转子叶片上下游可调叶片角度均对转子负荷有着显著的影响，且相邻下游叶片影响更为敏感。可调叶片调节角度不合理可能引起转子负荷异常升高，导致叶尖区域流动不稳定进而诱发叶尖旋转失稳现象。当旋转失稳的频率与叶片固有频率匹配时，叶片应力短时间内显著增大，存在导致叶片疲劳裂纹的风险。

3） 控制转子叶尖负荷可以避免出现非同步振动，优化转子叶片邻近可调叶片角度是排除非同步振动的有效手段。