搭建思维台阶 打造高效学堂

金晶

［摘 要］基于学生的认知水平及规律，从学习进阶理论出发，文章以“竖直平面内临界条件”问题教学为例，搭建使学生从低水平层级逐步到达高水平层级的教学台阶，使学生的思维逐层深入，进而有效提高学生的思维能力。另外，提出了分析竖直平面内临界条件的方法——“两点法”，方便学生抓住解题的关键和本质。

［关键词］思维进阶；圆周运动；临界条件；两点法

［中图分类号］    G633.7        ［文献标识码］    A        ［文章编号］    1674-6058（2023）14-0056-04

一、教学背景

学习进阶理论认为，学习是一个不断积累、不断发展的过程，学生对某一主题或核心概念的理解不是一蹴而就的，而是要经历许多个不同的中间状态，逐层进阶，从“浅表”走向“深度”的过程［1］。要求教师在教学过程中依据学生的认知及思维发展规律，从学生学习的需求和体验出发，优化教学过程，循序渐进，不断升入，逐步提高学生的思维深度。引导学生理解核心概念的本质，促进学生思维能力的提升，进而提升学生解决实际问题的能力与高阶思维能力［2］。

习题课教学作为课堂教学的重要组成部分，对培养学生学科核心素养的作用是毋庸置疑的。习题课教学可以加深学生对习题本质的理解，提高学生解题的灵活程度。因此，教师应该将思维进阶的相关理论应用到习题课教学中，从基本问题出发，引导学生层层深入地对问题进行探究，这样有助于学生重构原有知识并深化对原有知识内在逻辑的認知，形成严谨的思维习惯［3-4］。

圆周运动是高中物理教学的重要模型之一，是高考考查的热点。竖直平面内圆周运动的临界问题因其联系广、综合性强的特点，成为教学中的重点和难点，这些因素要求教师在教学中搭建进阶台阶，逐级深化，找到竖直轨道上各点的共性和联系，灵活运用相关规律解决实际问题。本文从一道习题出发，沿着逐级进阶的教学路径引导学生理解问题的本质，促进学生核心素养的提升。

二、教学过程中的学习进阶分析

（一）进阶起点与目标

通过前期学习，学生已经知道可以用“绳模型”和“杆模型”的相关知识处理竖直平面内圆周运动的临界问题，形成了解决该类问题的基本思路，可以解决一些简单的常规问题。但这两种模型通常只能用来解决最高点的临界问题，学生对临界条件的认知比较浅显，有的学生甚至只是死记结论，没有抓住问题的本质，对知识的整合和简化有所欠缺，对临界条件的认知出现了偏差，不能灵活应用。有的教师在分析此类运动模型时不够全面，不利于学生物理学科核心素养的发展。基于以上原因，在相关教学中，应注意搭建进阶台阶，逐级深化，找到竖直平面内轨道各点的共性和联系，灵活地运用相关规律解决实际问题。

（二）进阶障碍与困难

一方面，为了快速简便解题，不少学生省略了受力分析这一重要步骤，直接根据记忆列举临界条件，由于没有理解临界条件的本质，经常写错临界条件，从而导致“满盘皆错”。另一方面，学生对动能定理的理解不够深刻，在运用动能定理求解相关物理量时出现困难。

三、学习进阶层级与设计

明确教学起点和目标，结合教学过程中了解到的学生在学习中遇到的实际难点与障碍，设计了如下的教学活动，以引导学生层层深入，逐级进阶。

进阶1.搭建基本模型，构建圆周运动的基本特征

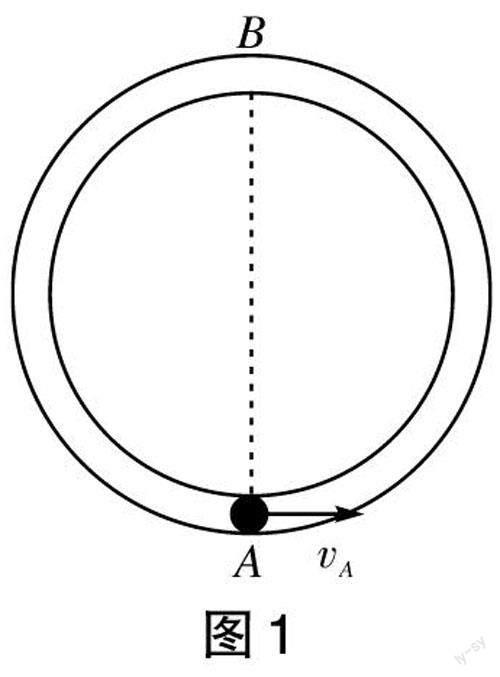
［例1］如图1所示，圆管形轨道固定在竖直平面内，轨道半径为R，光滑小球（直径略小于圆管直径）放置于轨道的最低点A，质量为[m]。现给光滑小球一水平向右的初速度[vA]，若要使光滑小球可以在竖直平面内做完整的圆周运动，初速度[vA]要满足什么条件？已知重力加速度为[g]。

学生活动：根据题意判断模型种类，尝试自己寻找该题的临界条件，个别学生回答。

分析：该模型属于典型的“杆模型”。在最低点给小球一个初速度[vA]，由于小球的惯性和轨道的支撑力，小球会沿着轨道向上运动。小球在竖直平面内运动时，轨道对小球有支撑力作用，使得小球不可能做近心运动，只要它能到达竖直平面内速度最小的点，就能在竖直面内做完整的圆周运动。由能量关系分析可知小球在最高点[B]时的速度最小，即[B]点为该题的临界点。故小球刚好在竖直平面内做完整圆周运动的临界条件为：小球在最高点时的速度为0。

［   参   考   文   献   ］

［1］  陈东晓，周洪伟. 基于学习进阶的教学构建：以“电动势”教学为案例［J］.丽水学院学报， 2021（5）：105-111.

［2］  郜攀. 基于深度学习的习题课教学：以“动能定理的运用”为例［J］.中学物理教学参考，2020（26）：38-40.

［3］  潘照萍.基于学习进阶理论的物理复习课教学设计：以“功能关系在力学中的应用”为例［J］.物理教学探讨，2017（4）：49-11，15.

［4］  韩叙虹， 姜连国. 基于学习进阶的翻转课堂教学设计：以“向心加速度”一节教学为例［J］.中学物理教学参考，2016（9）：41-44.

（责任编辑 易志毅）

［基金项目］安庆市2021年度教育科学规划研究项目（AJKT2021-098）。