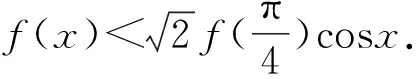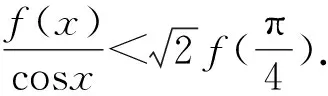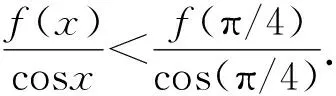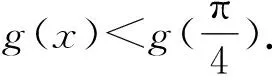利用导数研究常见四类不等式问题
2023-08-30马青莲马宇超魏俊潮
马青莲 马宇超 魏俊潮
(扬州大学数学科学学院,江苏 扬州 225002)
马宇超,男,硕士研究生,从事数学教学研究;
魏俊潮,男,博士,教授,从事数学教学研究.
不等式问题是高考数学的常见问题,结合函数命题常需要构造函数,导数是研究函数性质的利器,可更好地帮助学生分析问题、解决问题.常见的题型有比较大小、解不等式恒成立、证明不等式成立、解不等式这四类.本文结合近几年的高考题和各地模拟题,对这四类问题的解决方法进行探究.
1 利用导数比较大小
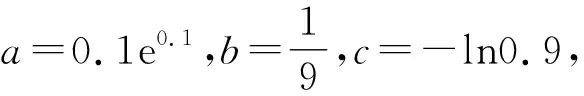
A.a C.c 令f(x)=ln(1+x)-x(x>-1), 当x∈(-1,0)时,f′(x)>0; 当x∈(0,+∞)时,f′(x)<0, 所以函数f(x)在(-1,0)单调递增,在(0,+∞)单调递减. 即b>c. (2)c=-ln0.9=-ln(1-0.1), 令h(x)=ex(x2-1)+1,则 h′(x)=ex(x2+2x-1). 所以g(0.1)>g(0)=0. 即0.1e0.1>-ln0.9. 所以a>c. 构造h(x)=(1-x)ex,h′(x)=-xex, 当x>0时,h′(x)<0,h(x)单调递减, 所以h(0.1) 所以a 综上可得c 评注对于这类无法直接比较大小的情况,首先需要观察已知表达式的特点并进行整理[1],使表达式的数字部分相互建立联系,其次将数字部分统一为自变量x,作差或作商构造关于x的函数,最后求导判断函数的单调性和函数值情况进行求解. 当x>0时,x2-2x+1≥0, 即x(x-2)≥-1. 所以φ(x)在(0,+∞)上单调递增. 又φ(2)=0,故当0 当x>2时,h′(x)>0,h(x)单调递增. 评注对于参数易于分离的不等式可使用分离参数法,将原不等式分离参数,转化为不含参数的函数的最值问题,利用导数进行求解.部分题目判断函数单调性时需要二次甚至三次求导,在求导函数时要注意导函数与原函数的对应关系,导函数的正负对应原函数的增减. 例3(2021年全国乙卷)设函数f(x)=ln(a-x),已知x=0是函数y=xf(x)的极值点. (1)求a; 解析(1)a=1; 当x∈(0,1)时,f(x)=ln(1-x)<0,所以xf(x)<0; 当x∈(-∞,0)时,f(x)=ln(1-x)>0,所以xf(x)<0. 只需证x+f(x)>xf(x), 只需证x+ln(1-x)>xln(1-x), 只需证x+(1-x)ln(1-x)>0即可. 令h(x)=x+(1-x)ln(1-x),则 h′(x)=-ln(1-x). 当x∈(0,1)时,h′(x)>0,h(x)单调递增, 当x∈(-∞,0)时,h′(x)<0,h(x)单调递减, 所以当x∈(-∞,0)∪(0,1)时,h(x)>h(0)=0,即x+(1-x)ln(1-x)>0在(-∞,0)∪(0,1)上恒成立,即证g(x)<1. 评注求导判断单调性时,一定要注意原函数的定义域,仅判断定义域内的函数单调性即可,避免部分导函数在定义域范围外的正负不易判断的情况,使简单问题复杂化. g′(x)<0. 所以g(x)是偶函数. 故选B. 评注不同区间上导函数正负的判断难度不同,若已知原函数的奇偶性和周期性,可巧用函数的奇偶性和周期性简化判断.此时可选择易于判断导函数正负的区间,再利用对称区间上奇函数单调性相同、偶函数单调性相反,周期函数各个周期上的函数单调性相同进行判断. 导数作为研究函数的强有力工具,可将函数单调性、极值和最值问题转化为导函数的符号进行求解.本文针对比较大小、解不等式恒成立、证明不等式和解不等式这四类常见的不等式问题进行了研究,总结了利用导数研究这类问题的做题方法和注意事项,希望能对学生有所帮助.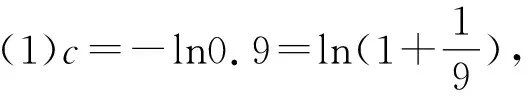
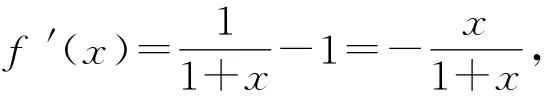
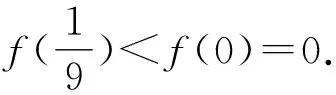
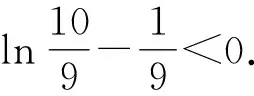
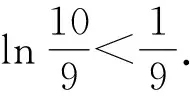
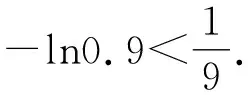
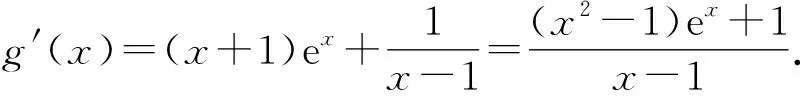
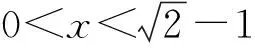
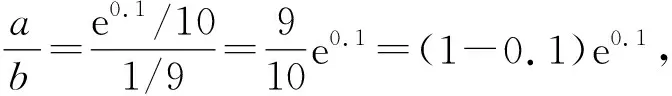
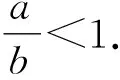
2 利用导数解不等式恒成立问题
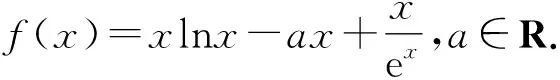

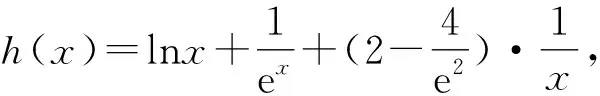
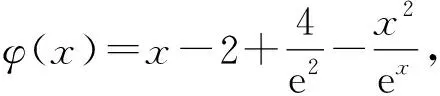



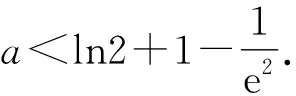
3 利用导数证明不等式
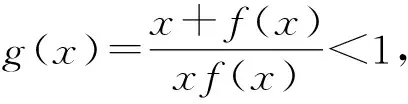
4 利用导数解不等式