巧用“三观”妙解三角恒等变换问题——以2022年新高考全国Ⅰ卷第18题为例

蔡双湖

(福建省安溪第八中学,福建 泉州 362402)

解三角形问题往往与平面几何、函数与方程、三角函数、平面向量、基本不等式等相关知识点交汇.三角恒等式变换是进一步研究三角函数图象和性质、正弦定理和余弦定理及其应用的基础,它是解决三角函数相关问题的必要知识和能力.全面贯彻新课标“知识交汇命题”的指导思想,是高考数学命题的一个基本考点,备受各方关注.以2022年新高考全国Ⅰ卷第18题为例,抓住常用三角函数公式的处理方法和变换方向,帮助学生进一步掌握三角恒等式变换的基本技能,积累三角恒等式转换的基本经验,从而提高解决问题的能力[1].

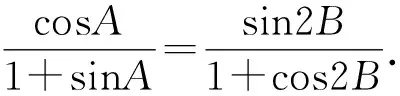
1 观角

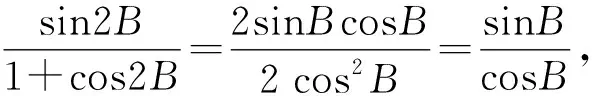
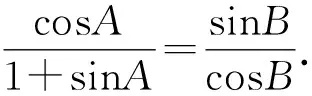
所以cosAcosB=sinB+sinAsinB.

所以cosAcosB-sinAsinB=sinB.

即cos(A+B)=sinB.

所以cos(π-C)=sinB.

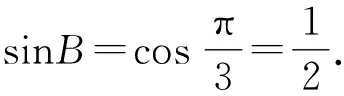
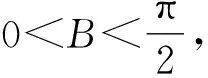
解法2由A+B+C=π,得

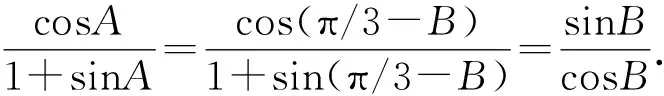
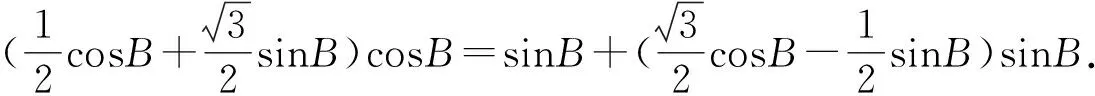
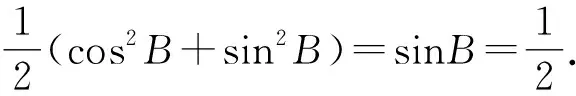
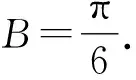
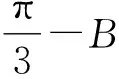
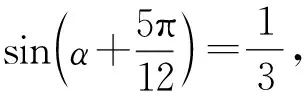
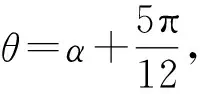
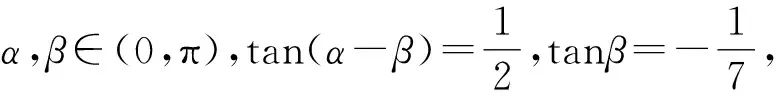
解析利用两次变角α=(α-β)+β,2α-β=(α-β)+α.

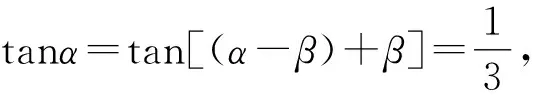
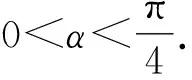
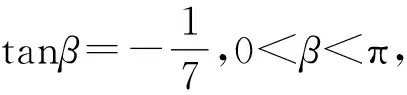
所以-π<2α-β<0.

因为tan(2α-β)=tan[(α-β)+α]=1,

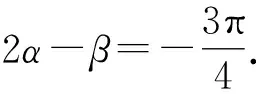
2 观名

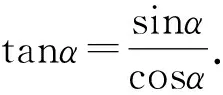
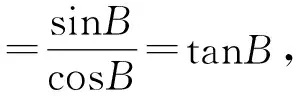
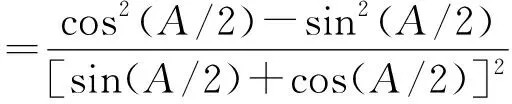
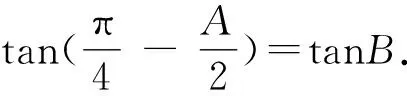
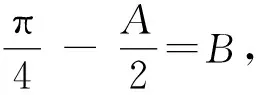
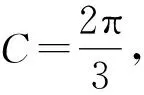
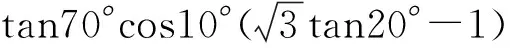
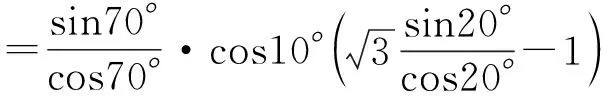
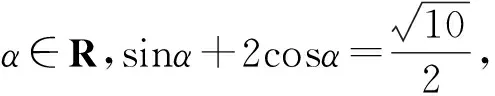
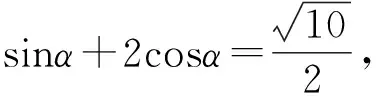
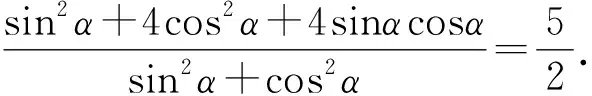
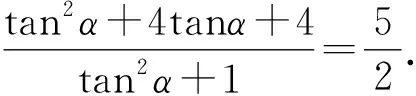
整理,得3tan2α-8tanα-3=0.

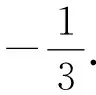
3 观结构

要熟悉三角恒等变换的各个公式的结构特征以及各种变形,像升幂、降幂,和差化积、积化和差,辅助角公式.

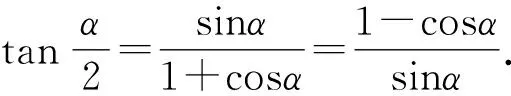
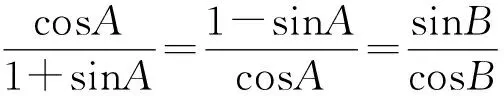
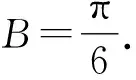
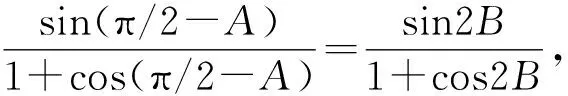
所以f(x)在(0,π)单调递增.

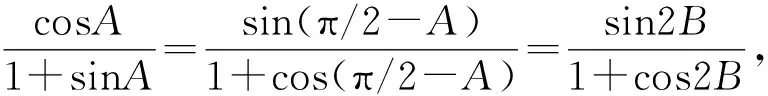
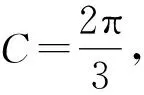
练习5(2023年新高考全国Ⅰ卷第17题第(1)问)已知在△ABC中,A+B=3C,2sin(A-C)=sinB．求sinA.

解析因为A+B=3C,所以π-C=3C.

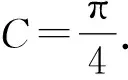
又2sin(A-C)=sinB=sin(A+C),

所以2sinAcosC-2cosAsinC=sinAcosC+cosAsinC.

所以sinAcosC=3cosAsinC.

所以sinA=3cosA.即tanA=3.

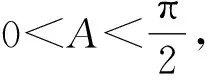
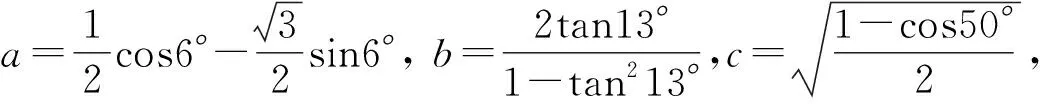
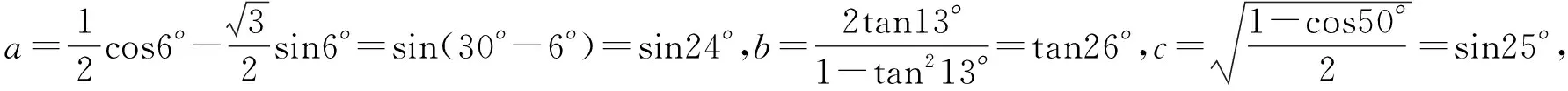
因为sin26°

综上所述,本文以2022年新高考全国Ⅰ卷第18题为例,抓住常用三角函数公式的处理方法和变换方向,梳理了三角恒等式变换的基本技能,积累三角恒等式转换的基本经验,总结了解决三角恒等变换问题的三个常见视角:观角、观名、观结构.因此,在日常教学中,不仅要总结常见的结论,还要注意结论的推导,明白变化的本质,加深对数学知识的理解,实现对数学知识的建构,积累基本数学活动的经验,达到对基本技能的掌握,增强运用数学知识解决问题的能力.