基于优化GM(1,N)模型的油气管道腐蚀速率预测
2023-08-29赵年峰夏艳权崔凯强孔淑颖梁昌晶
赵年峰,夏艳权,崔凯强,孔淑颖,解 静,梁昌晶
(1.中国石油集团渤海石油装备制造有限公司石油机械厂,河北 任丘 062552;2.河北华北石油工程建设有限公司,河北 任丘 062552;3.国家管网集团西南管道有限责任公司 南宁输油气分公司,南宁 530200;4.中国石油长庆油田分公司伴生气综合利用项目部,西安 710016)
腐蚀是油气管道失效的主要原因之一,管道一旦发生穿孔泄漏事故,将对油气田企业和周围环境造成重大影响。引发腐蚀的因素众多,因素之间具有多重非线性特征,科学有效地预测腐蚀发展趋势,及时采取适当的防腐措施,对于一定程度上降低管道失效带来的风险具有重要意义[1-2]。目前,有关管道腐蚀预测的模型有回归分析模型、神经网络模型和灰色模型(GM)等[3-4],其中回归分析模型的精度较低,对于非线性关系拟合效果较差;神经网络模型需要大量的数据支撑,对于小样本数据回归精度不高,经常出现欠拟合现象;灰色模型可用于少数据、贫信息的数据预测,适用于油气管道腐蚀这类样本规律不明显但系统内部发展明确的预测。当前灰色模型多以GM(1,1)模型为主,例如,李昊燃等[5]从无偏灰色、新陈代谢等方面对GM(1,1)模型进行了改进;王庆锋[6]将GM(1,1)模型与马尔科夫链相结合,通过状态转移矩阵,预测下一时间的腐蚀状态;张新生等[7]对GM(1,1)模型的尾端残差进行了修正,改变了预测趋势的惯性作用。但以上研究未能反映腐蚀因素对腐蚀速率的影响,模型具有一定的局限性。
基于此,本研究采用斯皮尔曼相关系数寻找腐蚀因素中相关性较高的变量,通过随机森林(RF)对变量重要性进行排序,去除相关性较高但重要性较低的变量,将优化后的变量输入GM(1,N)模型,采用人工蜂群算法(ABC)对GM(1,N)模型的背景值进行动态优化,最后对预测值和实际值的差异进行检验分析。研究结果可为管道防腐措施的制定提供技术指导。
1 数学模型
1.1 斯皮尔曼相关系数
斯皮尔曼相关系数通过两个变量间的等级关系确定相关关系,不受样本数据分布和样本容量影响,且对于缺失值和极值分布的存在具有较好的适应性,斯皮尔曼相关系数公式为
式中:rs——斯皮尔曼相关系数;
n——样本容量;
di——两变量间的等级差值。
1.2 RF重要度评价
RF 在进行数据选取训练决策树时,对输入样本进行了多次有放回的抽样,但总有一些样本无法参与决策树训练,这部分样本称为袋外数据[8]。RF 进行重要度评价的原理是计算袋外数据在每棵决策树上的贡献度,然后取平均值,即
式中:I——重要度指标;
M——决策树个数;
Error2i——第i个决策树的干扰信号;
Error1i——第i个决策树的袋外数据误差,当加入干扰信号后,I值下降幅度较大,则说明该变量的重要程度较高。
1.3 GM(1,N)模型
GM(1,N)模型是多维灰色模型,其中“1”为1 阶,“N”为变量个数,包括1 个自变量和n-1个因变量[9-10]。
设x1(0)为自变量序列,即x1(0)=(x1(0)(1),x1(0)(2),…,x1(0)(n)),因变量序列为
对原始序列xi(0)进行一阶累加形成xi(1),即
其中,i=1,2,…,n;l=1,2,…,k。
随后生成x1(1)紧邻均值序列z1(1),即
建立微分方程
该式即为GM(1,N)模型,a为发展系数,bi为驱动系数。通过最小二乘法估计a和bi的参数值,并将数据重新进行一阶累减还原得到序列的预测值。
1.4 模型评价
为了确定模型预测结果的可靠性,采用相对误差检验法评价模型精度。计算残差、相对误差和平均相对误差等三个指标,评价标准见表1。

表1 模型精度检验评价标准
2 GM(1,N)模型优化
经研究表明,GM(1,N)模型的误差关键在于公式(4)中背景值的构造存在缺陷,公式(4)是用相邻空间步长对应的梯形面积(黑色实线与底边围成的面积)近似代替积分区域面积(红色实线与底边围成的面积),如图1所示。当处理某些剧烈变化的数据序列时,误差较大。基于此,采用动态背景系数λ(i)替代公式(4)中的“0.5”,通过动态调整各区间的背景系数,最大程度降低背景值误差,即
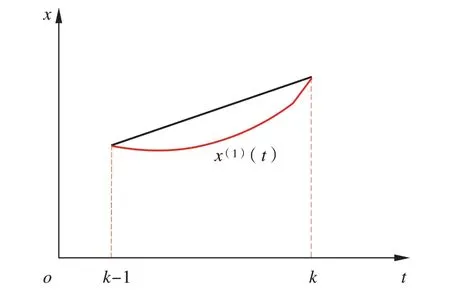
图1 背景值误差来源
对于λ(i)的选取原则是要使自变量预测值与实际值的误差最小,等同于多峰多维函数寻优问题。在此,采用人工蜂群算法(ABC)进行求解[11-12],算法步骤如下:
(1)初始化种群。根据公式(7)产生蜜源的初始位置,即目标函数的可行域,根据公式(8)计算各蜜源的初始适应度值。
式中:xij——第j维空间的第i个解;
xminj、xmaxj——第j维空间解的下限和上限;
fit(i)——第i个解的适应度值;
f(i)——第i个解的目标函数值。
(2)采蜜蜂根据公式(9)在蜜源附近进行局部搜索,形成新的位置vij,并根据公式(8)更新各蜜源的适应度值,将更新后的适应度值与之前的进行比较,并根据贪婪选择策略保留较好的解。
式中:Φij——(-1,1)的正态随机数。
(3)观察蜂在蜂房中等待采蜜蜂的蜜源信息,然后根据概率筛选蜜源。
(4)当采蜜蜂和观察蜂对搜索空间内的解均搜索完毕后,如一个蜜源的适应度值还没有提高,则放弃该蜜源,采蜜蜂变为侦查蜂,重新寻找新蜜源。
(5)迭代次数达到设定的最大迭代次数时,算法停止,否则转移至步骤(2)循环执行。
3 实例分析
以某Φ355.6 mm×6.3 mm 埋地输气管道为例,设计压力3 MPa,运行压力2.5 MPa。对管道沿线某处采用实地挂片的方式监测腐蚀速率,通过挂片与管道之间进行电性连接模拟防腐层破损点,保证该点的阴极保护电位和管道一致。在相同埋深处埋置12 组挂片,每组3 个,每30 天取一组挂片数据,序号1为第1天监测数据,序号2 为第30 天监测数据,以此类推,计算每组挂片的平均腐蚀速率,结果见表2。
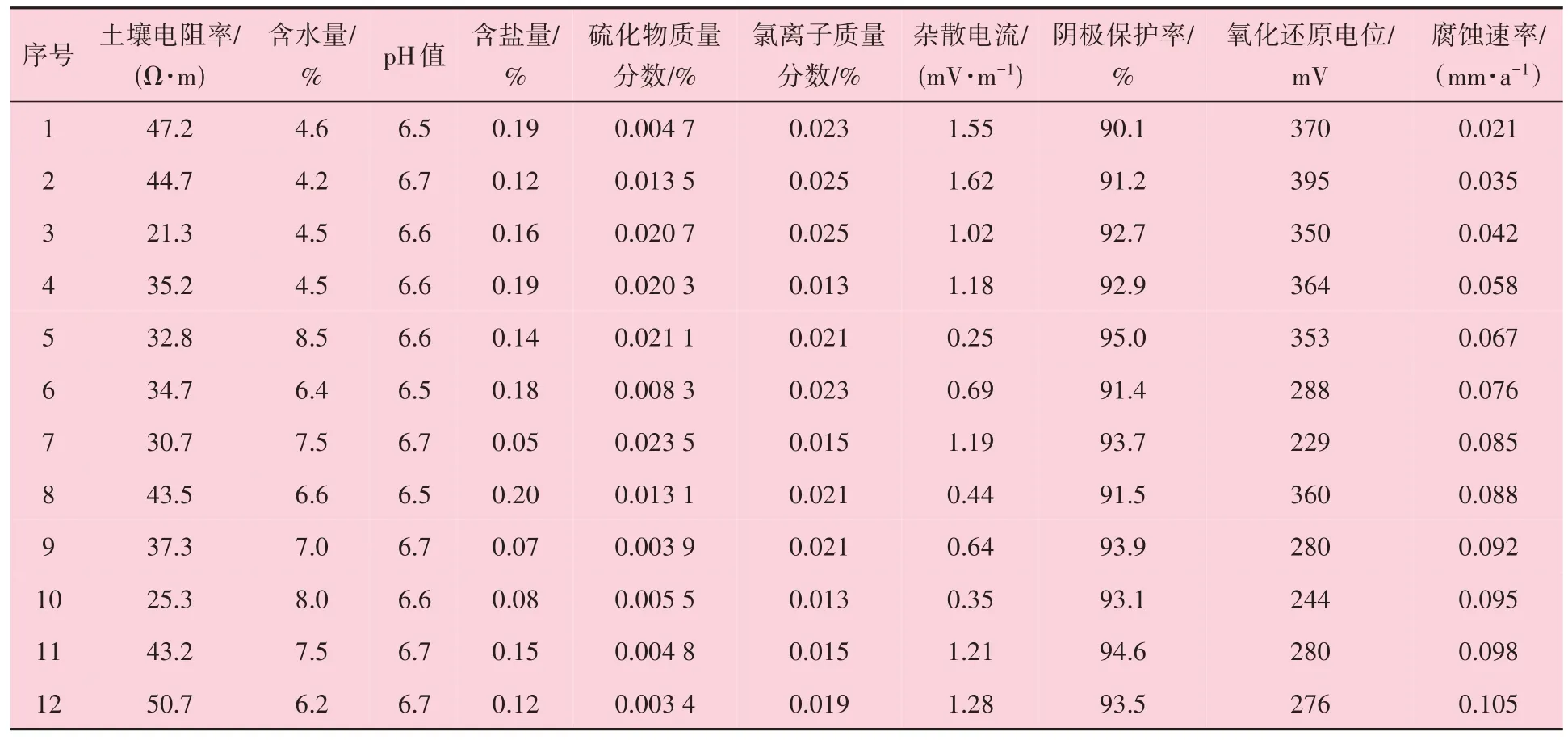
表2 管道腐蚀速率和相关影响因素
3.1 数据预处理
采用公式(1)计算表2 中影响因素的斯皮尔曼相关系数,结果见表3。筛选相关系数大于0.55 的变量,含盐量与氯离子质量分数的相关系数、pH 值和氧化还原电位的相关系数均超过了0.55。
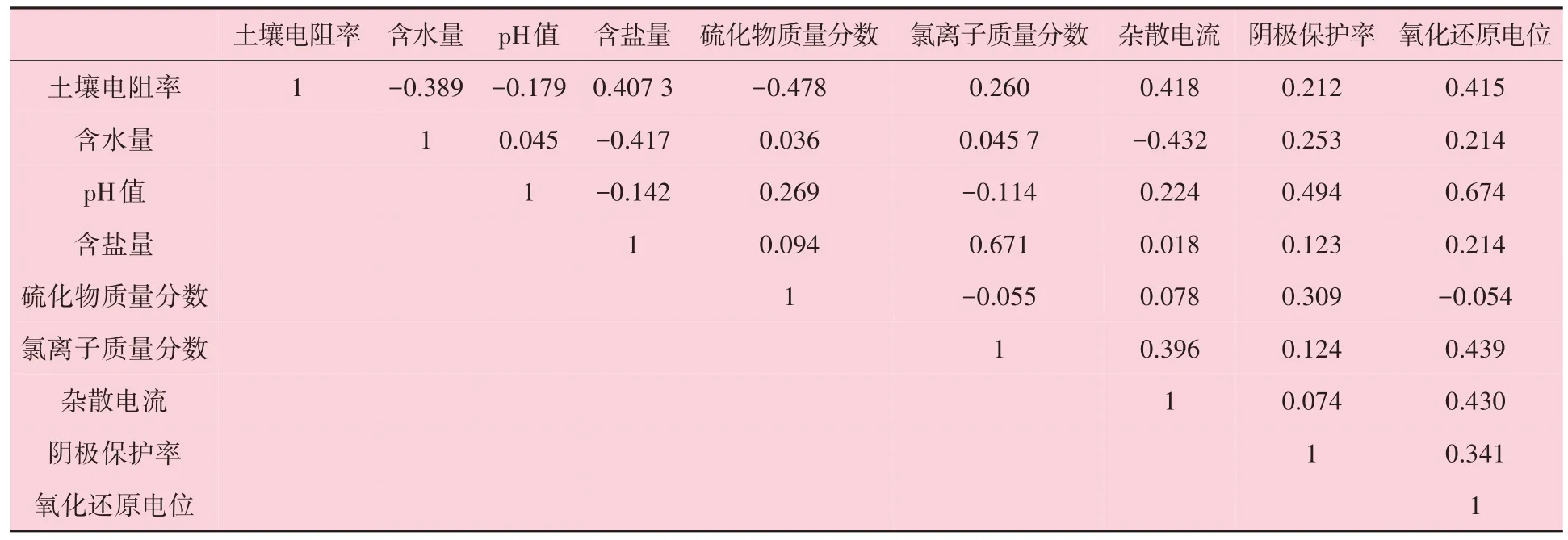
表3 斯皮尔曼相关系数矩阵
采用极差法对表2数据进行标准化处理,在最大决策树100的条件下,考察不同叶节点个数对结果均方误差的影响,结果如图2所示。当叶节点个数为5时,模型的均方误差最低,当决策树个数为80时,均方误差基本不再变化。因此,确定模型中叶节点个数5,决策树个数80。
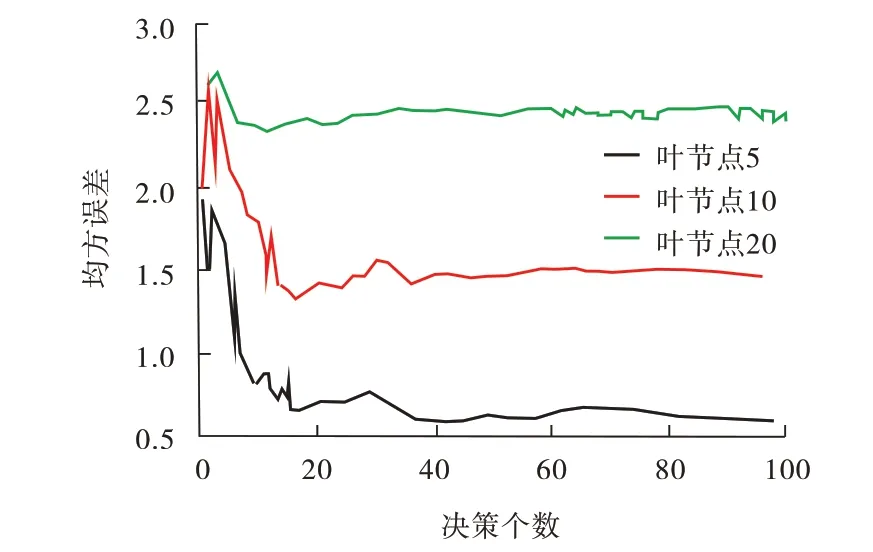
图2 RF模型参数优选
按照上述模型对变量进行重要度评价,结果如图3 所示。由图3 可知,变量重要度排序从大到小依次为土壤电阻率、含盐量、氧化还原电位、含水量、pH 值、氯离子质量分数、硫化物质量分数、阴极保护率和杂散电流,根据之前的相关系数分析,删除相关性较高但重要度较低的变量,故剔除氯离子质量分数和pH 值,这两个变量可以间接的通过含盐量和氧化还原电位反映。此外,阴极保护率和杂散电流的重要性较小,且表1中的阴极保护率均超过了90%,杂散电流均小于2.5 mV/m,说明管道在土壤中的最小保护电位基本满足规范要求,阴极保护失效对腐蚀的影响作用不大,管道周边不存在直流电气化铁路、有轨电车、直流电焊机等直流接地装置。最终确定GM(1,N)模型的因变量为土壤电阻率、含盐量、氧化还原电位、含水量和硫化物质量分数。
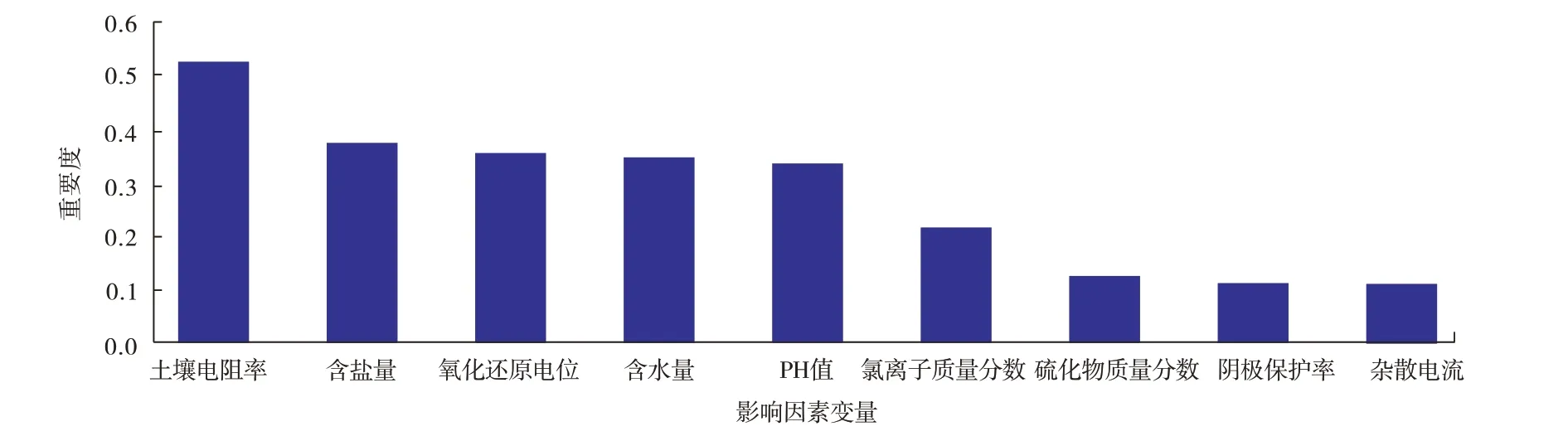
图3 变量重要度排序
3.2 训练精度检验
根据前文分析结果,N 取6,建立GM(1,6)模型,为了验证变量筛选的必要性,同时建立GM(1,10)模型(即未进行变量筛选建立的GM模型)。取前8组数据建立预测模型,通过后4组数据进行模型评价,参数列的计算结果见表4。

表4 参数列计算结果
在计算动态背景系数λ(i)时,蜂群数量为20,蜜源数量为10,搜索限制为20 次,最大迭代次数为100次,此时待优化问题的目标函数为10 维。为保证算法准确性,反复运行10 次,取误差最小的一次作为最终结果,算法在迭代至50次左右收敛,迭代过程如图4所示。最终得到优化GM(1,6)的λ(i)为0.214 7、0.014 5、0.058 9、0.075 2、0.165 4、0.987 5、0.069 52。
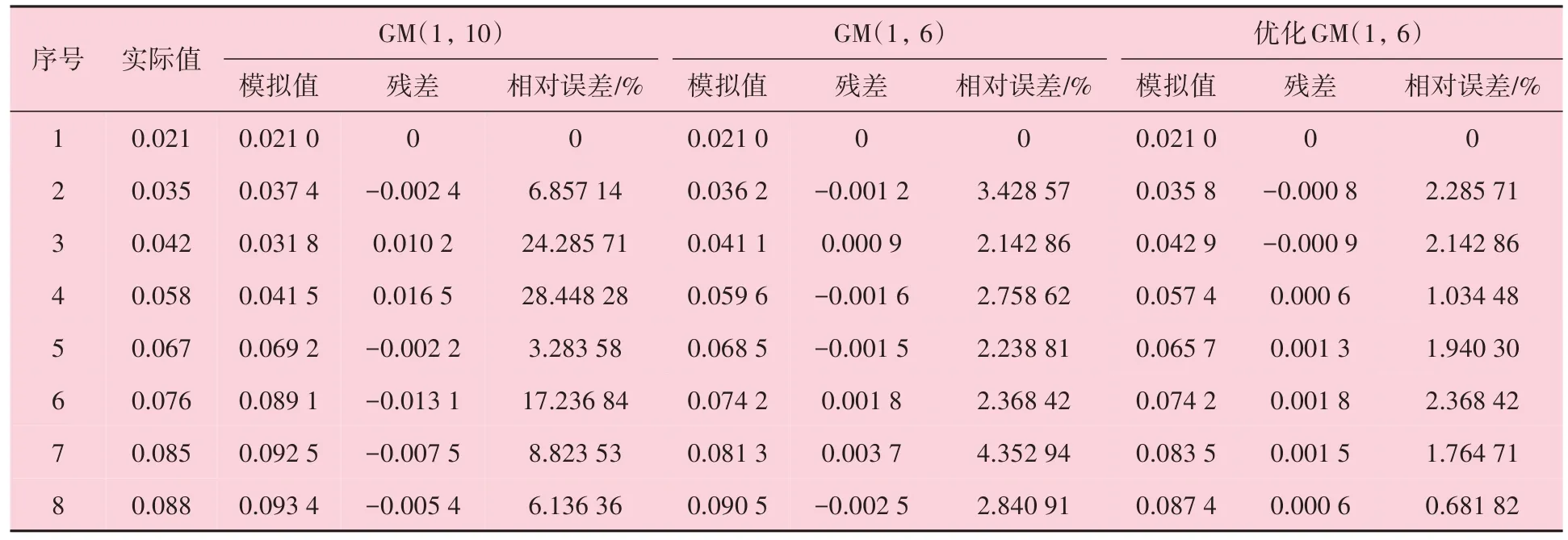
GM(1,10)GM(1,6)优化GM(1,6)序号实际值1 2 3 4 5 6 7 8 0.021 0.035 0.042 0.058 0.067 0.076 0.085 0.088模拟值0.021 0 0.037 4 0.031 8 0.041 5 0.069 2 0.089 1 0.092 5 0.093 4残差0-0.002 4 0.010 2 0.016 5-0.002 2-0.013 1-0.007 5-0.005 4相对误差/%0 6.857 14 24.285 71 28.448 28 3.283 58 17.236 84 8.823 53 6.136 36模拟值0.021 0 0.036 2 0.041 1 0.059 6 0.068 5 0.074 2 0.081 3 0.090 5残差0-0.001 2 0.000 9-0.001 6-0.001 5 0.001 8 0.003 7-0.002 5相对误差/%0 3.428 57 2.142 86 2.758 62 2.238 81 2.368 42 4.352 94 2.840 91模拟值0.021 0 0.035 8 0.042 9 0.057 4 0.065 7 0.074 2 0.083 5 0.087 4残差0-0.000 8-0.000 9 0.000 6 0.001 3 0.001 8 0.001 5 0.000 6相对误差/%0 2.285 71 2.142 86 1.034 48 1.940 30 2.368 42 1.764 71 0.681 82
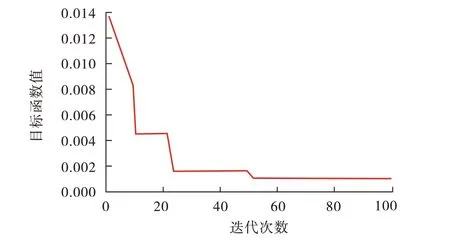
图4 ABC算法迭代过程
三种模型腐蚀速率训练精度对比结果见表5。GM(1,10)模型除了第5 个样本相对误差较小,其余均较大,平均相对误差为11.88%,对照表1为“勉强”等级。GM(1,6)和优化GM(1,6)模型训练阶段的平均相对误差分别为2.51%和1.52%,两者均达到了表1中“好”等级。
表5 腐蚀速率训练值与误差分析
同理,将GM模型中N按照图3的排序依次增加氯离子质量分数和pH 值,构成GM(1,7)和GM(1,8)模型,统计训练样本的平均相对误差,结果如图5所示。由图5可见,增加变量后,平均相对误差增大,说明了变量间的冗余性对预测精度有较大影响,采用斯皮尔曼相关系数和随机森林对变量进行筛选具有必要性。优化GM(1,6)模型的训练精度最高,可以进行下一步的预测。
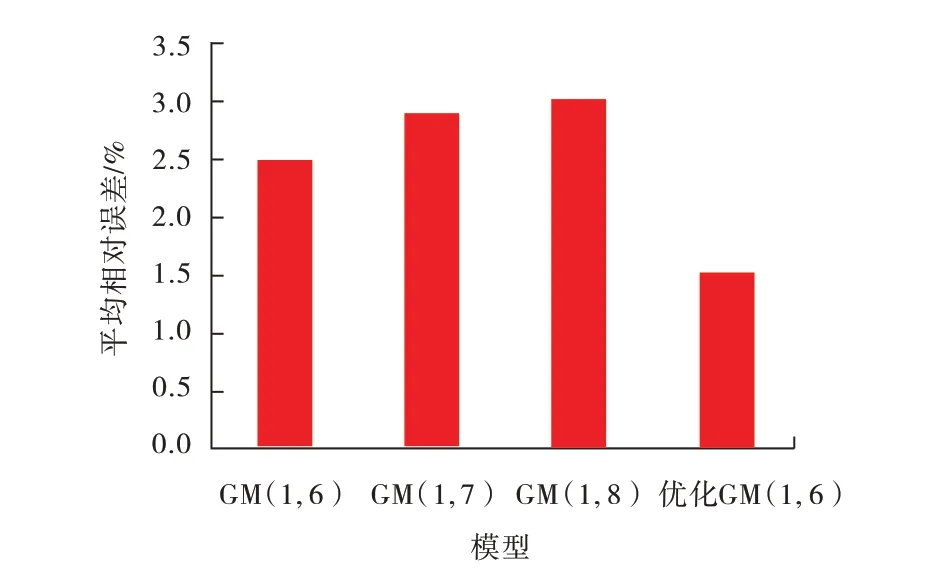
图5 不同模型的平均相对误差对比
3.3 预测精度检验
根据上述训练模型,对后4组数据进行预测和模型评价,结果见表6和图6。其中,GM(1,10)模型预测值的相对误差均在10%以上,且围绕实际值上下波动,说明影响腐蚀速率的因变量中存在较多的相关冗余信息,这些信息使模型拟合困难,导致误差较大;GM(1,6)模型在预测阶段的相对误差和数据波动逐渐增大,说明该模型不适合长期预测,当腐蚀速率发生较大变化时,下一时刻预测结果往往是前一时刻结果的延续;优化GM(1,6)模型的相对误差大幅降低,预测值与实际值吻合较好,可以根据训练时建立的非线性关系及时对预测结果进行调整。GM(1,10)模型、GM(1,6)和优化GM(1,6)模型预测阶段的平均相对误差分别为15.61%、9.74%和2.03%,分别对应“勉强”、“合格”和“好”等级,说明优化后的GM(1,6)模型在训练样本和预测样本上的表现均较好,不存在欠拟合的现象。
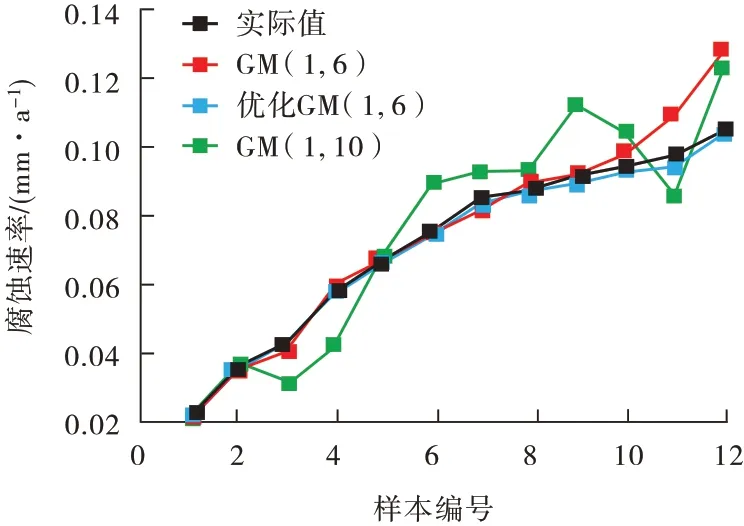
图6 不同模型预测结果对比
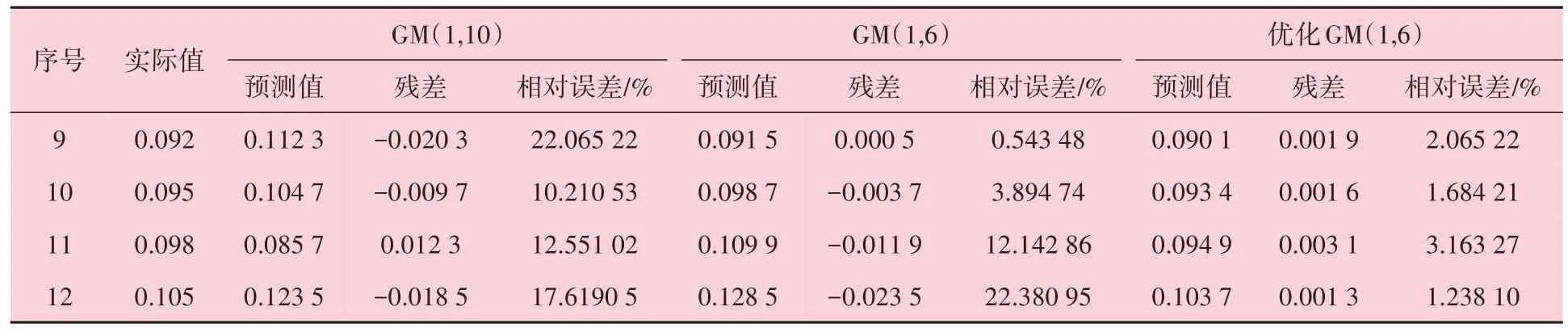
表6 腐蚀速率预测值与误差分析
4 结 论
(1)针对单变量模型预测管道腐蚀速率方面的局限性,建立了GM(1,N)模型,通过斯皮尔曼相关系数和RF 算法对因变量进行筛选,降低因变量相关性对自变量预测结果的影响,最终选取5个因素作为因变量,变量重要度排序从大到小依次为土壤电阻率、含盐量、氧化还原电位、含水量和硫化物质量分数。
(2)针对GM(1,N)模型背景值构造存在的缺陷,引入动态背景系数,采用人工蜂群算法对最佳背景系数进行寻优,实现对腐蚀速率的准确预测。
(3)相比GM(1,10)模型和GM(1,6)模型,优化GM(1,6)模型在训练阶段和预测阶段的平均相对误差大幅降低,分别为1.52%和2.03%,预测结果更接近实际值,可为油气管道重点部位的腐蚀防护提供实际参考。
