高速冲击下特殊螺纹接头动态响应特性研究*
2023-08-29苑清英晁利宁杨晓龙年晨阳
苑清英,晁利宁,余 晗,杨晓龙,汪 强,年晨阳
(1.中油国家石油天然气管材工程技术研究中心有限公司,西安 710018;2.中国石油宝鸡石油钢管有限责任公司,陕西 宝鸡 721008;3.西安石油大学 石油工程学院,西安 710065;4.宝鸡钢管西安专用管公司,西安 710200)
0 前 言
随着我国对油气资源需求的日益增大,油气田的开采已经向更深层、更苛刻的井况发展。目前国内低压、低渗透、稠油热采、高含硫天然气以及页岩气井开采量逐年升高,这些资源的勘探开发利用难度大,对油套管柱的要求也越来越高[1]。特殊螺纹接头就是针对这些苛刻井况开发的油井管产品[2]。
与传统的API螺纹相比,特殊螺纹接头具有连接强度高、密封性能好的优点,满足拉伸、压缩、内压、外压以及扭转等油田复杂载荷工况[3]。在这些苛刻条件下,检验特殊螺纹的密封性能显得尤为重要。通常工程上应用实验室复合加载评价系统,来模拟油田工况[4],然而在试验过程中,复合加载设备由于焊接端塞的断裂,引起的巨大反冲击力是否对特殊螺纹的密封性能造成影响,是否会造成接头泄漏,实验室模拟比较困难,也难以定量衡量[5]。鉴于此,数值模拟仿真技术成为解决该问题的有效手段,利用有限元仿真,不但可以模拟端塞断裂后造成的冲击载荷对特殊螺纹接头结构的影响,定量分析所关注的结构部位的应力应变分布情况,而且可以对特殊螺纹接头不断优化和改进,从而降低试验频率,缩短试验周期,对节约生产成本具有重要的意义[6]。
本研究采用Abaqus/Expilct 显式求解器,对受冲击载荷并且发生复杂相互接触作用的特殊螺纹接头进行瞬间动态响应分析,定量分析冲击载荷对密封面接触压力的影响,为特殊螺纹接头的设计和优化以及实验室试制提供理论依据和技术支持[7-10]。
1 有限元分析
1.1 分析对象
本研究选用的特殊螺纹接头结构如图1 所示,采用的是球面对锥面金属过盈的密封形式,台肩处采用负角度结构形式,连接螺纹为BJC型,套管规格为Φ114.3 mm×8.56 mm(接箍直径133.35 mm),钢级为P110,其材料参数见表1。

表1 P110套管材料性能参数
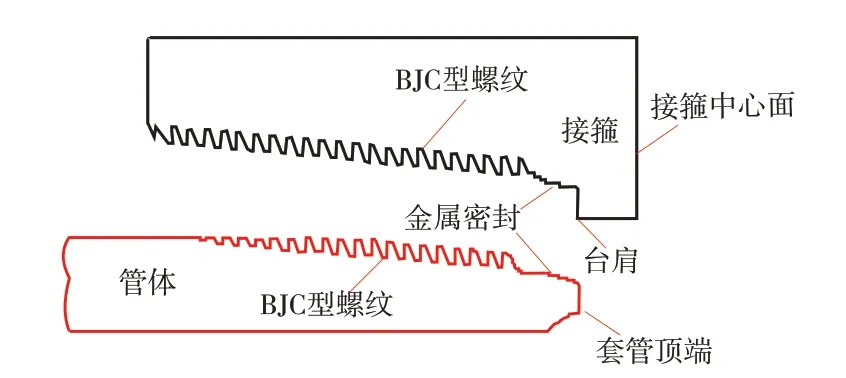
图1 特殊螺纹接头结构示意图
1.2 基本假设
特殊螺纹接头是一个复杂的三维结构,三维模型可以较好地模拟管体拧入接箍从而实现连接的过程,真实地反映螺纹空间分布以及螺旋升角。但是由于特殊螺纹三维模型网格数量多且接触复杂,计算效率低,精度较差,难以满足工程实际应用的需要。
本研究采用2D 轴对称模型进行分析,对有限元模型进行几点假设和简化:①管体和接箍二者均为各向同性材料;②忽略连接螺纹的螺旋升角的影响。
1.3 网格剖分
采用弹塑性非线性模型对其进行网格剖分。管体和接箍均选用四节点轴对称单元,管体总单元数为75 219 个,接箍总单元数为83 760 个。管体底端约束轴向位移,接箍和管体过盈配合。
1.4 边界条件及载荷施加
(1)由于模型具有对称性,其接箍的中心面轴向位移为0,在接箍中心面上施加轴向位移约束,如图2所示。

图2 边界条件及载荷施加
(2)在上卸扣的基础上,利用载荷幅值曲线模拟冲击效应,在短时间内进行加载并卸载,分析管体以及接箍密封面处的应力应变、接触压力以及载荷时间历程曲线,并观察管体和接箍密封面的动态响应。
2 非线性动力学有限元模型计算
特殊螺纹接头焊接端塞在做复合加载试验时突然断裂,管体受持续时间较短的冲击载荷时,巨大的反冲击力对接头结构变形造成一定的影响,因此必须考虑结构的几何大变形对结构整体刚度的影响,也就是几何非线性影响[11]。对于高速冲击问题即非线性动力学,采用显式积分法更加合适。显式积分法主要求解应力波传递问题,介质受到初始扰动后,其边界或者内界的某个小区域会逐渐向介质内部或者周围进行传播[12]。显式积分法采用一次一个单元的方式扩展,在求解过程中不需要求解切线刚度矩阵,不需要进行复杂的迭代求解,耗费时间较少,且容易收敛,计算效率高。
非线性动力学分析求解的基本方程为
式中:M——质量矩阵;
I——粘性效应项(考虑阻尼、粘塑、粘弹等效应);
C——阻尼矩阵;
K——刚度矩阵;
P(t)——外部激励作用;
u(t)——节点位移向量。
ABAQUS中显式动力学分析采用直接积分法求解上述方程,也就是按照时间历程对上述微分方程直接进行数值积分。考虑到非线性效应动力学问题,需要对动力学方程进行直接时间积分。
(1)节点计算[13]动力平衡方程
对时间显式积分
(2)单元计算
汇集节点内力It+Δt,设置t+ Δt为t,返回到步骤1。
3 计算结果及分析
3.1 等效应力及接触压力分布
对于管体受到高速冲击,采用*Dynamic,Explicit分析,结果如图3所示。

图3 等效应力分布云图
从图3可以看出,管体受到冲击载荷的时候,最大等效应力出现在接箍的第三牙处,最大值为913 MPa。密封面处应力均不大,为335~552 MPa。
密封面及台肩处接触压力分布如图4所示。受到冲击载荷的时候,最大接触压力出现在台肩处,其最大值为2 476 MPa。密封面处接触压力分布范围为184~393 MPa。
3.2 密封面处接触压力对比
为了定量分析受高速冲击前后密封面处的接触压力大小,选择密封面处的一条路径PATH1(如图5所示)进行应力对比,对比结果如图6所示。
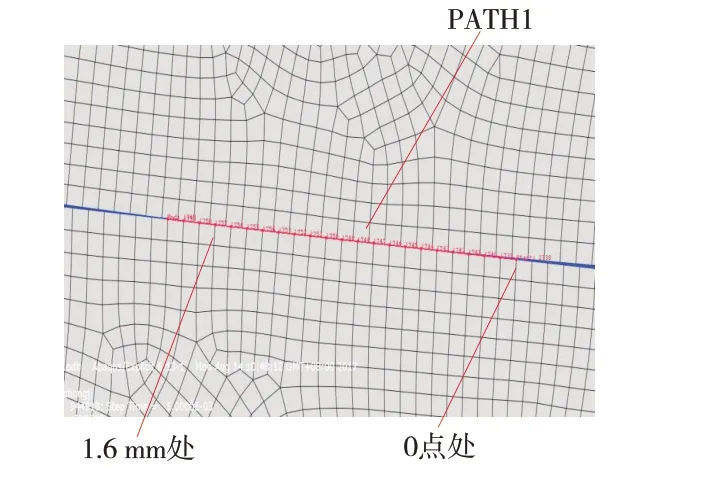
图5 密封面处的的路径PATH1
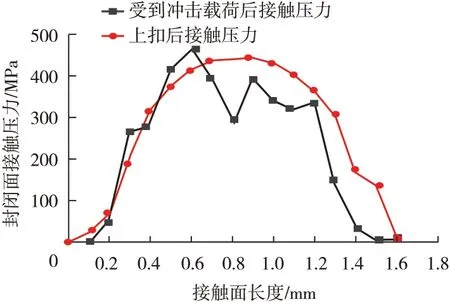
图6 密封面PATH1处接触压力对比
从图6可以看出,受到冲击载荷后,密封面处接触压力出现振荡,数值升高后又突然降低,受到冲击载荷后密封面接触压力的最大点位置发生了变化,得出最大接触点前移,而且数值也发生了变化,最大值为418.5 MPa。上扣完成后整个接触位置压力变化比较平滑,最大接触点出现在0.8 mm 处,最大接触压力为397.2 MPa。相对来说,受到冲击载荷后,接触压力略有升高,但是变化幅度不大。
密封面处的节点位移如图7所示,经过对比发现,受到冲击载荷后密封面处的节点位移普遍增大,比上完扣后的位移增大0.025 mm左右,说明冲击载荷对密封面处节点的位置有一定的影响。

图7 密封面PATH1处位移对比
密封面处等效应力对比如图8所示,对比受冲击载荷和上扣完成后的等效应力发现,由于冲击载荷的影响,密封面处的等效应力普遍高于上扣完成后的等效应力,但是两者的趋势基本一致。这是由于上扣完成后的等效应力主要是由于过盈所造成的应力,而在短时间内受到冲击载荷,再加上过盈配合,应力的叠加会导致等效应力升高。
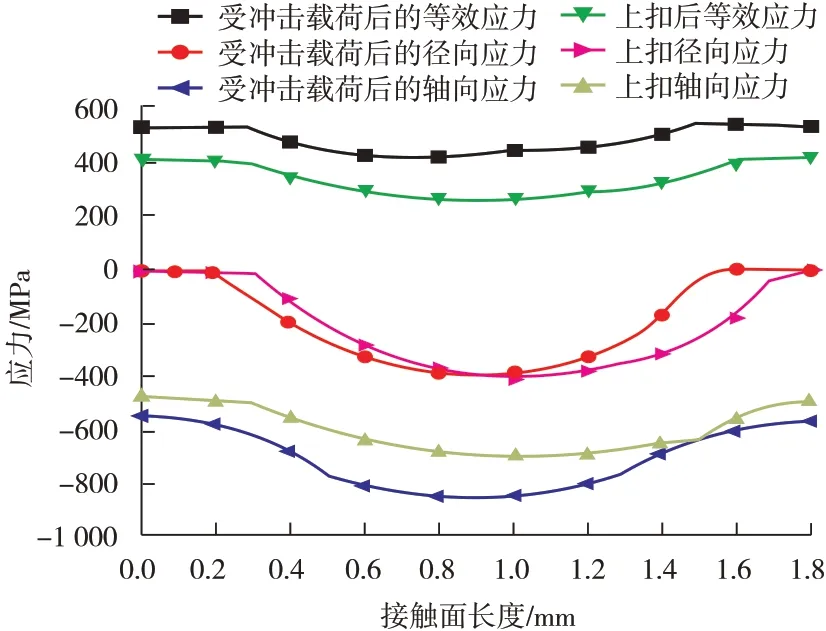
图8 密封面PATH1处等效应力对比
在冲击载荷作用之后,径向应力和轴向应力跟上扣完成后的径向、轴向应力分布趋势基本保持一致。可以看出,受冲击载荷的等效应力主要是由轴向应力造成的,轴向应力占主导地位。
3.3 台肩处接触压力对比
对台肩处的接触压力、位移以及等效应力进行分析,沿着PATH2路径(如图9所示)进行对比,对比结果如图10所示。从图10可以看出,由于管体受到轴向的冲击载荷,冲击载荷会使管体产生振动,因此在冲击载荷的作用下,台肩处的接触压力不是持续的变化,而是有一定的波动。台肩在轴向冲击力的作用下接触压力普遍高于上扣后的接触压力,其中最大接触压力达到1 310 MPa,而同样的接触位置,上扣后的接触压力为614 MPa,在整个台肩接触面上,接触压力普遍均匀,曲线比较光滑,波动较小。
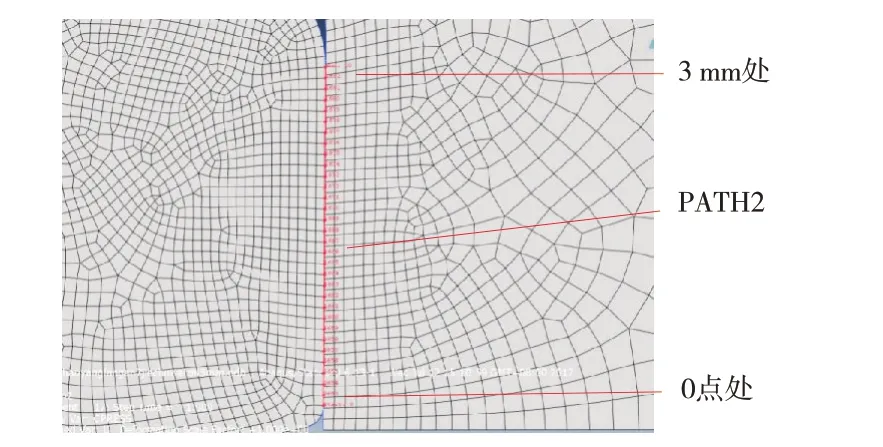
图9 台肩密封处的路径PATH2
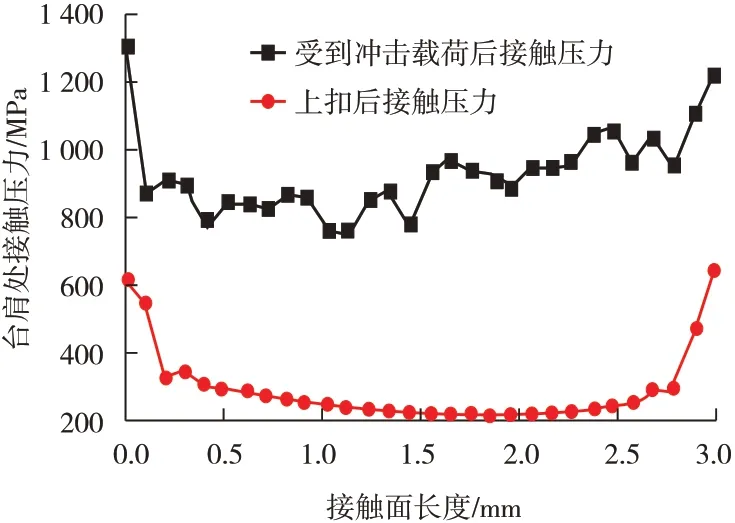
图10 台肩处沿路径PATH2接触压力对比
台肩处轴向位移对比如图11所示,从图11可以看出,受到冲击载荷后台肩处的节点位移普遍增大,比上完扣后的位移增大0.054 mm左右,说明冲击载荷对密封面处节点的位置有一定的影响。
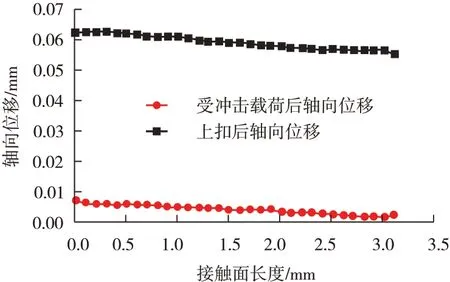
图11 台肩处沿路径PATH2轴向位移对比
台肩处应力对比如图12 所示,从图12可以看出,受冲击载荷后的等效应力比上扣后的等效应力大,受冲击载荷后台肩处的轴向应力处于主导作用,同时台肩处还受到径向应力的作用,此处的轴向应力普遍要比上扣后的轴向应力和径向应力高,应力的趋势基本一致。受冲击后台肩处的最大等效应力为758 MPa,上扣后台肩处的最大等效应力为426 MPa。
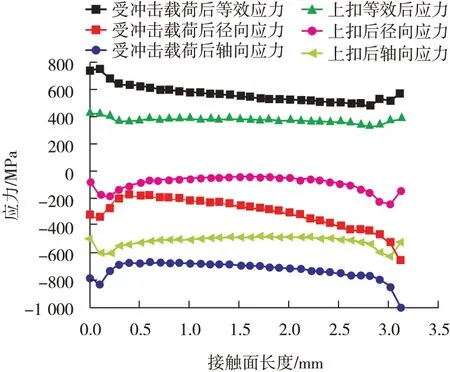
图12 台肩处沿PATH2处应力对比
能量变化历程能够真实地反映试验中冲击对特殊螺纹结构的影响。图13 和图14 分别为动能和内能随时间变化曲线。
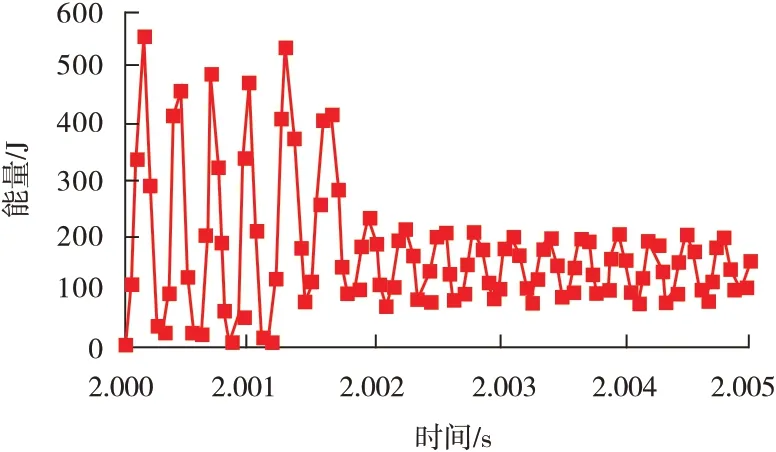
图13 动能随时间变化曲线
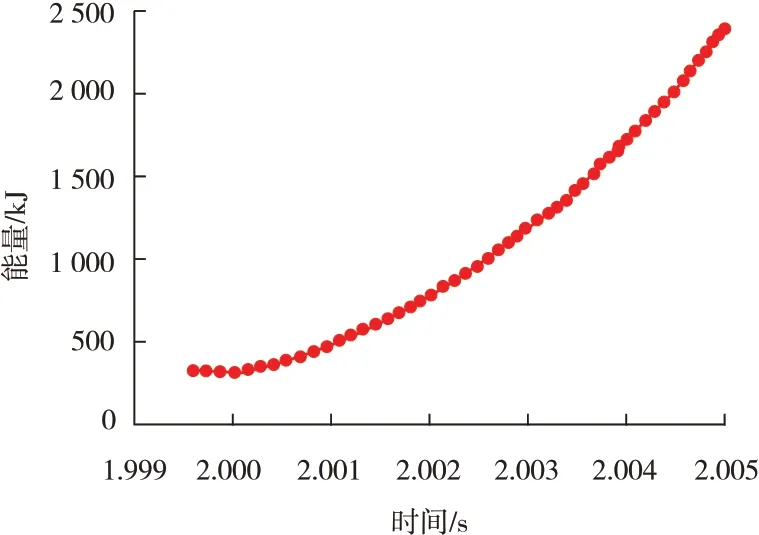
图14 内能随时间变化曲线
从图13可以看出,此结构假设无阻尼存在,因此结构会以恒定的振幅持续振动,而且振动会随着时间的增加趋于停止,在几十次振动后,振动便消失了,发生的能量损失主要是由于摩擦效果造成的。在默认情况下,总存在体粘性阻尼,但是由于体粘性阻尼很小,所以振动会持续很长一段时间。
同时可以看出,在整个结构受到冲击载荷时,结构动能总是上下波动,而且在有效时间内,波动并没有停止,因此,这种情形在图6中表现为密封面处接触压力出现波动,波动趋势跟动能的波动趋势一致,刚开始动能很大,随着时间的进行,由于摩擦力的损耗,能量开始慢慢变小,如果给予足够长的时间,最终会趋于静止。
从图14可以看出,随着冲击载荷的作用,内能逐渐增大,由于动能的作用,逐步转化成结构的变化以及阻尼引起的内能变化。此结构系统中,默认阻尼为体粘性阻尼,所以存在一定的能量消耗。
4 结 论
(1)受到高速冲击后套管特殊螺纹密封面处接触压力产生一些波动,但总体趋势跟上扣后一致,差别不大。密封面处的节点位移普遍增大,比上扣后的位移增大0.025 mm 左右,说明冲击载荷对密封面处节点的位置有一定的影响。
(2)密封面处的等效应力普遍高于上扣完成后的等效应力,但是两者的趋势基本一致。轴向冲击作用下台肩的接触压力普遍高于上扣后的接触压力,而同样的接触位置,在整个台肩接触面上,接触压力普遍均匀,曲线比较平滑,波动较小。
(3)台肩处的节点位移普遍增大,比上扣后的位移增大0.054 mm 左右,说明冲击载荷对密封面处节点的位置有一定的影响。
(4)台肩处等效应力比上扣后的等效应力大,台肩处的轴向应力处于主导作用,同时受到径向应力的作用,此处的轴向应力普遍要比上扣后的轴向应力和径向应力高,应力的趋势基本一致。
(5)从能量变化历程可以看出,特殊螺纹接头整个结构受到冲击载荷时,结构的动能总是处于上下波动,密封面处接触压力出现波动,波动趋势跟动能的波动趋势一致。
