某两栖火炮水上发射稳定性仿真及试验研究
2023-08-29崔青春宁变芳林文琦王在森
崔青春,宁变芳,林文琦,王在森
(西北机电工程研究所,陕西 咸阳 712099)
具有两栖作战能力的自行火炮是两栖登陆作战的重要武器装备,目前世界各国装备的两栖型自行火炮多为直瞄突击装备,射角通常不大于25°。研制具有海上间瞄射击功能的最大射角达到70°、射向360°的两栖自行压制火炮,适应不同海况的航渡安全性、射击安全和稳定性等研究至关重要。
段怡君等建立了带水翼的两栖火炮水上射击动力学模型,分析了有无水翼对车体稳定性的影响[1];郭昭蔚等以某轮式自行火炮为例,采用水动力无因次体系法对该自行火炮的水动力试验数据进行合理转换,运用MATLAB对轮式自行火炮水上射击动力学方程进行了解算,获得了火炮的水上射击位移规律[2]。以上文献均针对两栖车辆水上射击稳定性进行仿真计算,计算过程未涉及水的附加阻尼力及水中附加惯性矩的计算,同时也未涉及对模型验证。
为了分析某两栖自行压制火炮水上射击时发射安全性与稳定性,对纵稳性及横稳性进行了计算,建立了两栖火炮水上发射动力学方程,应用分步式迭代数值方法,有效解决了水动力变质量问题,获取了3种射击工况下火炮的运动响应及姿态角,结合水上射击试验火炮姿态角测试,对建立的水上发射动力学方程进行了验证。结果表明,高低0°射角条件下,纵向射击仿真与测试底盘最大纵摇角误差3.6%,横向射击最大横滚角误差2.7%,验证了发射动力学方程准确性及数值求解的计算精度,同时表明该两栖火炮具有良好的水上射击稳定性储备,为该两栖火炮水上发射安全性评估提供了理论依据。
1 稳性计算
1.1 横稳性计算
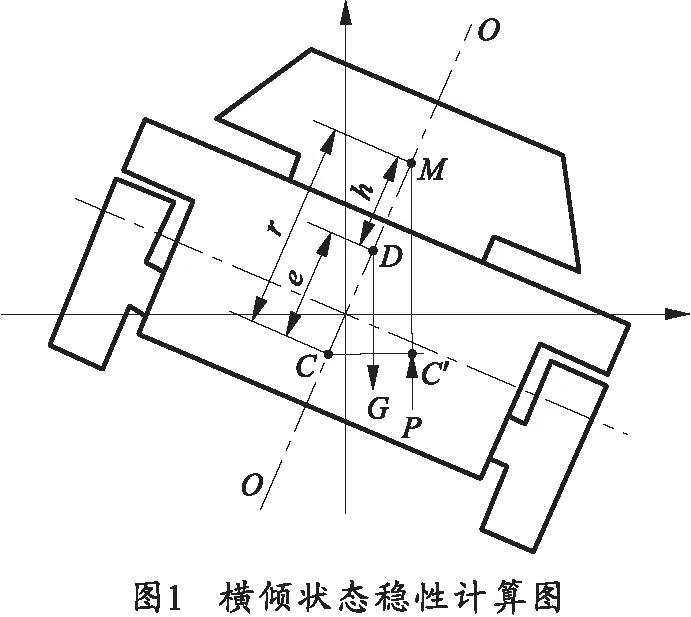
稳性是两栖车辆重要的水上性能之一,代表两栖车辆受到外力作用离开平衡位置,外力消除后恢复到平衡位置的能力。静稳性参数是水上射击车体稳定性计算的基础。
当两栖车辆浮在水面上处于平衡状态时,受到铅垂向下的重力G和铅垂向上的浮力P的作用,作用点分别在系统的重心D和浮心C上,通过重心D和浮心C的铅垂线O-O称为浮轴。重心D和浮心C之间的距离用e表示。当系统受到外界作用力干扰而发生微倾时,由于排开水的体积发生改变,重力G保持不变,浮心由C移到C′点,过C′作铅垂线,交浮轴O-O于M点,该称为稳心。浮心和稳心之间的距离CM(或C′M)称为稳心半径r。重心和稳心之间的距离DM称为稳心高度h,重力G和浮力P组成一个力偶,此力偶矩称为恢复力矩。受力示意如图1所示。
两栖车辆水线面面积对其横轴的惯性矩为[3]
(1)
式中:IB为水线面横向惯性矩;L和B分别为车体在水中浸润的水线长度和宽度。
横稳性半径为
(2)
式中,V为排水体积。
横稳性高为
(3)
式中,zD和zC分别为D、C两点垂直方向坐标。
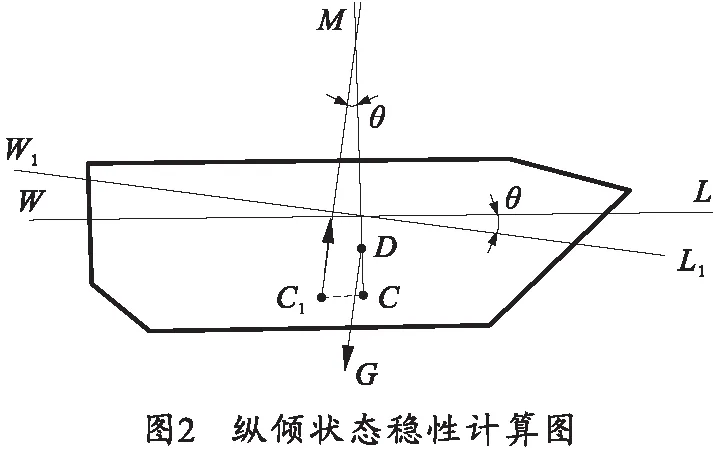
1.2 纵稳性计算
两栖车辆纵倾状态如图2所示,车辆水线面面积对其纵轴的惯性矩为[4]
(4)
式中,IL为水线面纵向惯性矩。
纵稳性半径为
(5)
纵稳性高为
(6)
2 水上射击动力学模型
2.1 水上射击动力学方程的建立
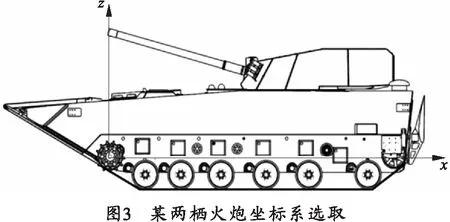
某两栖火炮水上射击动力学方程的建立采用刚体平动、定轴转动定理及平面力系分解原理建立[5-10],坐标轴原点取在车辆左右对称面主动轮中心位置,向后为x轴正向,向左为y轴正向,垂直向上为z轴正向。如图3所示。
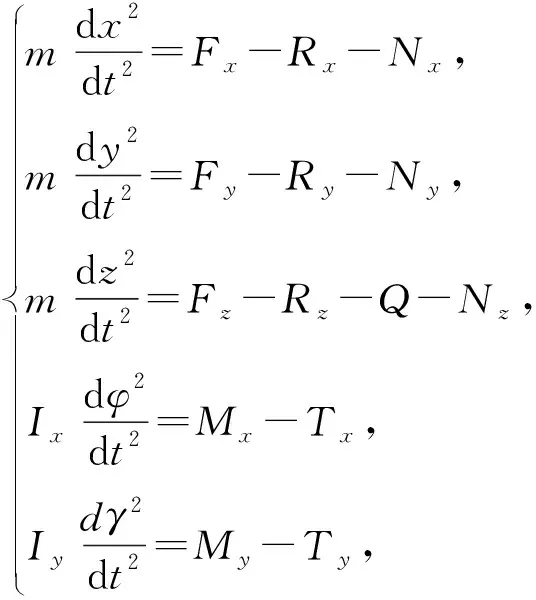
(7)
式中:x、y、z分别为对应坐标轴方向的位移;Fx、Fy、Fz分别为后坐力在对应轴方向的轴向分力;Rx、Ry、Rz分别为其速度矢量方向上的迎水阻力;Q为升沉方向的浮力产生的恢复力;Ix、Iy分别为沿纵轴线、横轴的线的惯性矩;Mx、My分别为后坐力产生的横滚和俯仰翻倒力矩;Tx、Ty分别为浮力产生的横滚和俯仰恢复力矩;φ、γ分别为俯仰、横滚角位移;m为整车惯性质量。
2.2 水上射击载荷
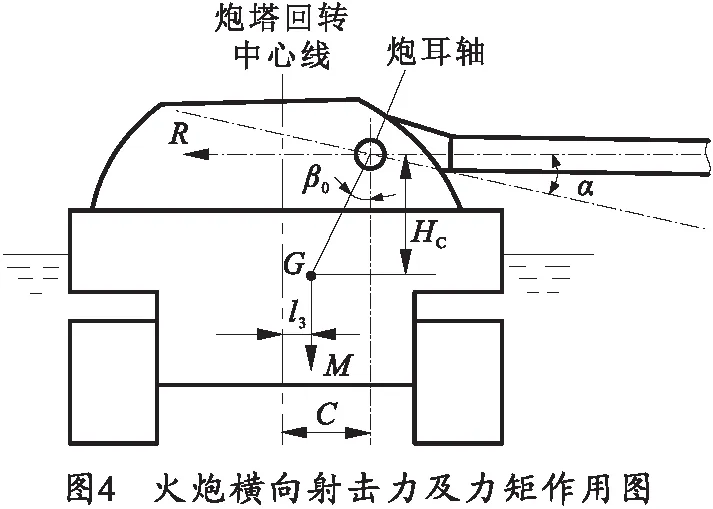
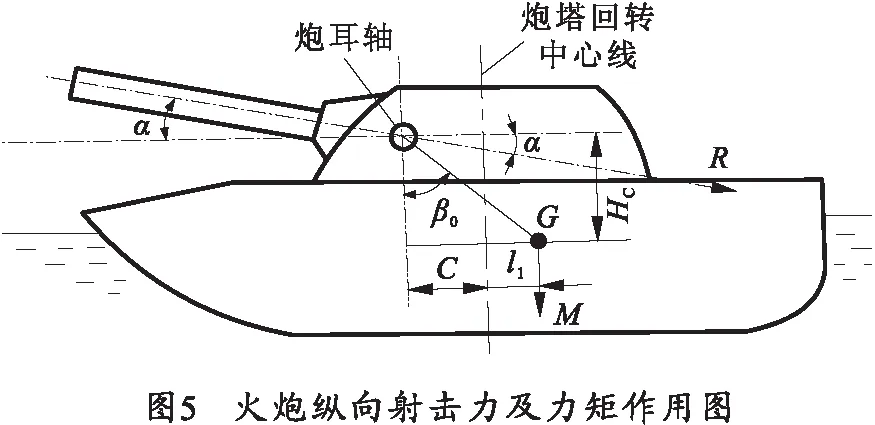
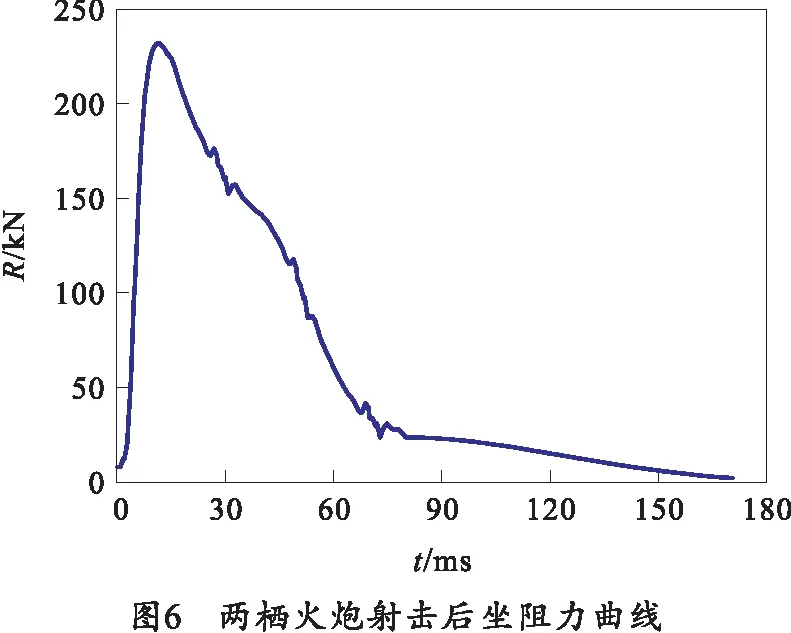
两栖战斗车辆水上横向射击时,射击载荷作用点为耳轴,作用方向与身管轴线平行,如图4、5所示,射击后坐阻力曲线如图6所示。
后坐阻力可分解为
(8)
式中:F为后坐阻力;α为高低射角;β为方位射角。
翻倒力矩为
(9)
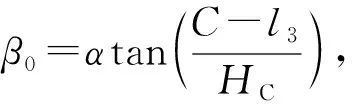
恢复力矩计算公式为
(10)
浮力计算公式为
Q=ρ(Vi-V)g,
(11)
式中:Vi为升沉时的排水体积;ρ为水的密度。
迎水阻力计算为
(12)
式中:Ax,Ay,Az分别为速度矢量方向的投影面积;CD为迎水阻力系数,根据巴普密尔近似公式计算得到:
(13)
式中:AM为中横剖面面积;Lr为去流段长度。
阻尼力矩计算为
(14)
式中,ξ为阻尼系数,
(15)
式中,d为幅值衰减比。
2.3 水中惯性矩计算
车辆在水中运动时与其周围的水相互作用,使水得到了动能,动能是以水的动压出现的,此种作用力产生了附加惯性力,一般附加惯性力与车辆的加速度成正比例关系,其比例系数称为附加质量或附加惯性矩。
横滚惯性矩:
Ix=Ix0+ΔIx1+ΔIx2,
(16)
式中:Ix为全车水中通过x轴总惯性矩;Ix0为车固有的横滚惯性矩;ΔIx1为车体带动水的附加惯性矩;ΔIx2为车辆行动部分带动水的附加惯性矩。
根据文献[3]中的公式知:
Ix0=ixV(B2+H2),
(17)
ΔIx1=ix1Ix0,
(18)
(19)
式中:ix与车辆形状质量分布相关系数;ix1为车体带动水的附加惯性矩系数;B1为履带中心距;b为履带宽;l为主动轮与导向轮纵向距离。
俯仰惯性矩:
Iy=Iy0+ΔIy1+ΔIy2,
(20)
式中:Iy为全车水中通过y轴总惯性矩;Iy0为车固有的俯仰惯性矩;ΔIy1为车体带动水的附加惯性矩;ΔIy2为车辆行动部分带动水的附加惯性矩。俯仰附加惯性矩的计算同横滚附加惯性矩计算方法。
3 不同射角射击工况计算
基于建立的两栖车辆水上发射动力学方程,采用四阶龙格-库塔法来对某两栖火炮在时域运动方程进行积分,应用分步式迭代数值方法,有效解决了水动力变质量问题。分别对方位0°高低0°、方位90°高低0°及方位0°高低70°这3种工况进行水上射击仿真计算,分析两栖火炮水上射击过程中的车辆的运动响应。其中高低0°射角时由于翻转力矩较大,重点关心底盘角位移,高低70°射角主要关心底盘升沉位移。
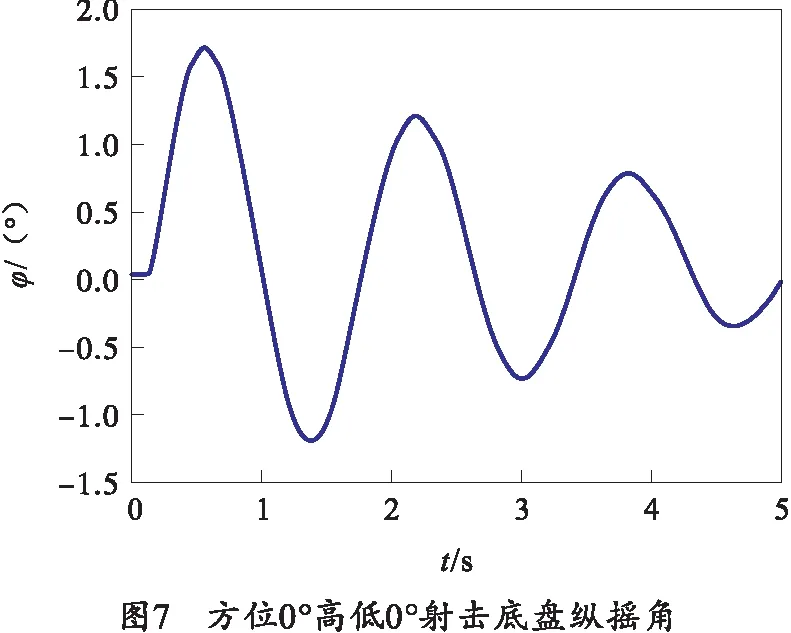
方位0°高低0°射击时,两栖火炮底盘纵摇角如图7所示。
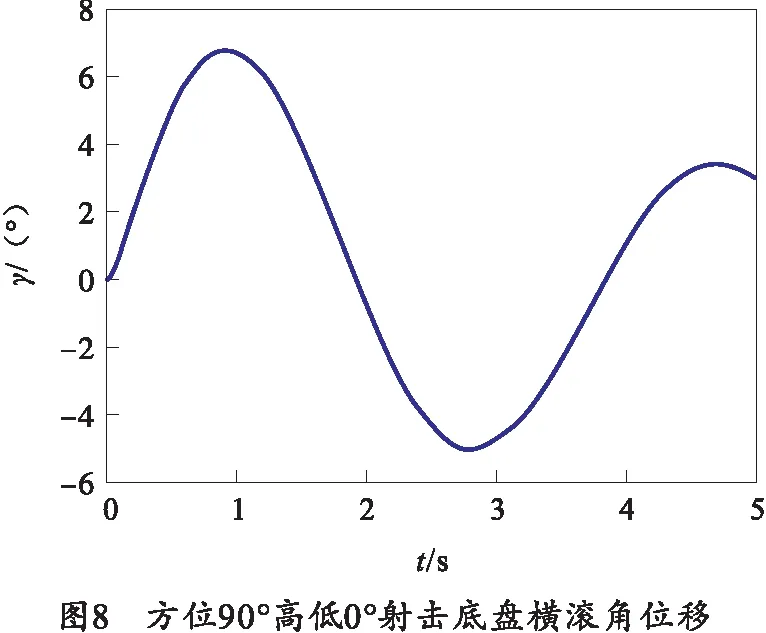
方位90°高低0°射击时,底盘横滚角如图8所示。
方位0°高低70°射击时,质心升沉位移如图9所示。

从计算结果可以看出:方位0°高低0°射击时,两栖火炮底盘最大纵摇角1.72°;方位90°高低0°射击时,两栖火炮底盘最大横滚角6.77°;方位0°高低70°射击时,火炮质心的最大下沉量为114 mm。参考中国船舶科学研究中心提出的舰船耐波性衡准值[11],单幅有义纵摇及横摇衡准值分别为4.8°及16°,因此该两栖火炮具有良好的水上射击稳定性。
4 水上射击试验测试结果对比
水上实弹射击试验在某舰船濒海科研试验基地进行,射击过程中的底盘角位移通过安装于底盘上的高精度陀螺角位移姿态传感器获得。方位0°高低0°及方位90°高低0°射击时的仿真计算及测试车体纵摇及横滚角位移对比曲线如图10、11所示,仿真与靶场测试结果对比如表1所示。
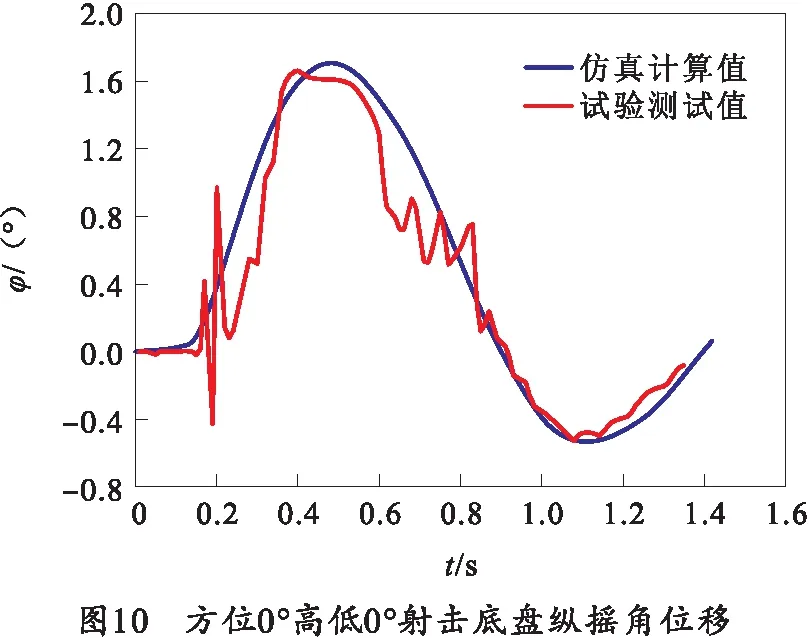
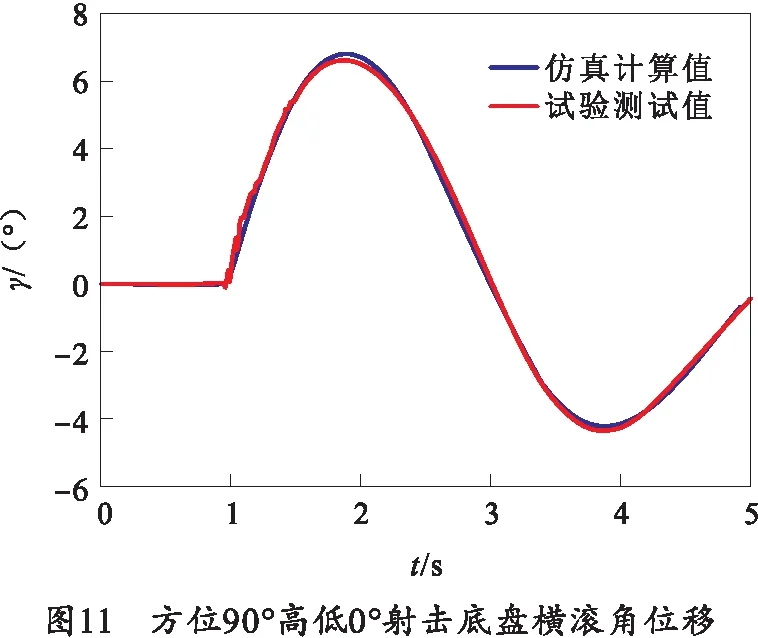

表1 仿真与测试角位移最大值对比
5 结论
1)在静水条件下,方位0°高低0°射角射击时的底盘纵摇角1.72°,方位90°高低0°横向射击时底盘横滚角6.77°,明显小于中国船舶科学研究中心提出的舰船单幅有义纵摇4.8°、横摇16°的耐波性衡准值,因此该武器系统具备良好的稳定性。
2)在静水条件下,方位0°高低70°射角射击时的火炮质心最大升沉位移约114 mm,不足最低干舷三分之一,具有较好的稳定性储备。
3)通过与水上实弹射击试验底盘姿态测试结果对比,方位0°高低0°射角仿真与测试底盘最大纵摇角误差3.6%,方位90°高低0°射角仿真与测试底盘最大横滚角误差2.7%,验证了发射动力学方程及数值仿真的计算精度。
