面向动态目标跟踪的全电坦克自适应鲁棒控制策略研究
2023-08-29陆浣清王修业孙芹芹王银龙陈雨
陆浣清,王修业,孙芹芹,王银龙,陈雨
(1.南京理工大学 机械工程学院,江苏 南京 210094;2.南京航空航天大学 能源与动力工程学院,江苏 南京 210016))
为提高坦克行进间的瞄准和射击精度,需要通过驱动和稳定坦克炮塔与发射系统,使坦克快速瞄准与精确跟踪[1-2]。由于全电坦克火炮稳定系统是一个由机械结构、伺服电机、电动缸和控制系统组成的系统,具有复杂的非线性、耦合性和不确定性[3-4],且目前坦克火炮控制方法的设计往往脱离真实模型,难以在高机动下保持良好的作战性能,因此,坦克稳定系统需要一种针对强非线性和不确定性的控制方法。
在坦克行进过程中,坦克火炮稳定系统的控制性能受外部干扰、参数摄动等非线性和不确定性因素的影响,为此近年来学者们关于火炮稳定系统动力学特性与系统非线性、时变性的研究逐渐展开[5-6]。陈宇等[7]基于动态协同仿真方法,建立了坦克行进间机电液联合仿真模型,考虑了主要的组成和受力,将其简化为底盘和火力两个部分,并上下座圈相连接,为坦克炮控系统设计及火炮稳定系统控制的研究提供了理论基础。Yuan等[8]采用连续摩擦模型描述非线性摩擦特性,利用反演方法提出了一种非线性自适应控制器来应对不确定性扰动,控制器在参数不确定性条件下具有渐近跟踪性能。
坦克稳定控制系统的控制策略对系统性能的影响同样显著。早期的稳定控制系统主要基于经典控制理论进行研究设计[9],随着现代控制理论的发展,智能控制算法在坦克火炮稳定控制方面也有相关应用。Qiao等[10]针对低速摩擦条件下坦克炮控系统目标跟踪问题,设计了反步滑模控制器,通过仿真验证该方法不需要摩擦的精确模型即可降低非线性因素的影响。Hu等[11]则将干扰观测器引入滑模控制以对外界干扰进行实时观测,仿真结果表明该控制策略能提高系统的跟踪性能和低速爬行性能,有效消除了滑模控制过程中的抖振问题。综上所述,为满足坦克火炮系统精准性、快速性和稳定性的需求,相关研究分布于探究坦克系统动力学特性、建立更为完善的坦克火炮系统动力学模型、设计先进的控制算法等方面[12-15]。
为此笔者在综合考虑系统非线性、耦合性和不确定性的基础上,开展基于动力学模型的火炮双向稳定自适应鲁棒控制策略研究,以全电坦克火炮双向稳定系统为控制对象,建立考虑执行机构作用的方位向和高低向执行器动力学模型,并以状态空间模型表达;在此基础上,综合考虑双向稳定系统中存在的参数摄动、传动误差和所受外界干扰等不确定因素,分析受控系统的不确定性边界条件,设计自适应律在线估计不确定性因素对系统性能的影响,进而设计自适应鲁棒控制器,实现对系统不确定性干扰的抑制;最后通过仿真研究进一步验证了提出的控制器的优良控制效果。
1 坦克行进间全电稳定系统建模
1.1 坦克火炮稳定系统数学模型
全电坦克炮双向稳定系统机械部分由方位向旋转的炮塔部分和垂直向摆动的发射系统部分构成。设τ1(t)、τ2(t)分别为方位向和高低向的力矩输入,θ1(t)、θ2(t)分别为火炮坐标系下炮塔和身管的旋转角度(即方位角和高低角),由欧拉-拉格朗日方程推导得到的坦克火炮稳定系统模型如下[16]
(1)
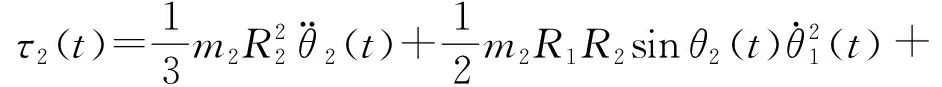
(2)

由模型(1)、(2)可见,火炮稳定系统是一个由方位向状态θ1和高低向状态θ2组成的非线性系统。真实的火炮稳定系统是一个由炮塔-发射系统、执行机构(如伺服电机系统、电动缸系统等)、控制系统等子系统耦合而成的综合性动态系统,因此后续将对稳定系统子系统进行分析,并进行控制器设计,设计思路更符合实际需求。
1.2 伺服电机驱动下方位向稳定系统动力学模型
方位向系统可看作由炮塔和电机组成的运动机构,引入伺服电机的动态方程[17]
(3)
Ta(t)=ktum(t)-keωm(t),
(4)
式中:ωm(t)为电动机角速度;Ta(t)为电动机转矩;Tm(t)为齿轮输入扭矩;um(t)为控制输入电压;J为电机转动惯量;Bm为电机轴粘滞阻尼系数;kt、ke分别为电机转矩系数和电动势系数与电枢电路总电阻的比值。
由于电机减速齿轮组之间存在间隙非线性,用dt(t)表示实际电机齿轮与传动齿轮之间存在传动误差,输出扭矩τ1(t)可以表达为[18]
τ1(t)=NTm(t)+dt(t),
(5)
式中,N为传动比。
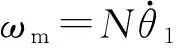
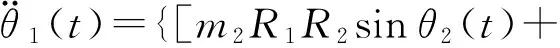
(6)
1.3 电动缸驱动下高低向稳定系统动力学模型
高低向稳定系统位置关系如图1所示,a为电动缸顶角,a0为电动缸初始角度,a=(θ2+a0),l0为电动缸初始长度,la为耳轴中心与电动缸在炮塔上安装位置之间的距离,ldt为电动缸与耳轴中心在支架上的驱动位置的距离。
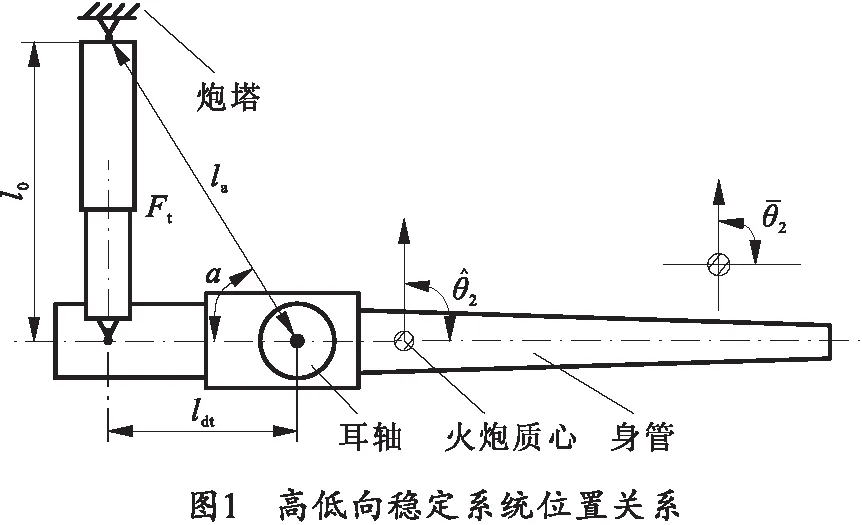
电动缸推杆位移可以表示为
(7)
(8)
根据电动缸动力学特性[19],电动缸对系统式(2)的输入转矩为
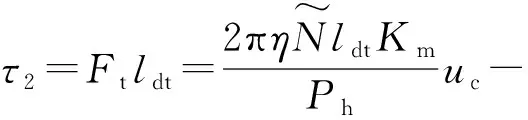
(9)
式中:Ft(t)为负载力;η为传动效率;Ja为电机转动惯量;Jb为驱动器转动惯量;Ba为电机轴粘滞阻尼系数;Bb为驱动器粘滞阻尼系数;θa(t)为电机输出旋转角度;uc(t)为控制输入;Km为电磁转矩系数与电枢电路总电阻的比值。
将式(8)、(9)代入式(2),可得全电驱动下火炮高低向稳定系统为
(10)
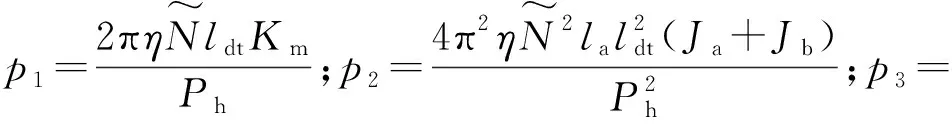
实际工作过程中,坦克双向稳定系统无可避免地存在着由建模误差、外界干扰、测量偏差、参数摄动和初始状态等导致的不确定性[20],这些不确定性极大地影响着火炮稳定系统的性能。
1.4 具有不确定性的火炮稳定系统动力学模型
针对火炮方位向系统式(6),考虑系统参数摄动、外界干扰等问题,将不确定性参数伺服电机转动惯量J,粘滞阻尼系数Bm,外界干扰d1以及传动误差dt,分解为
(11)

针对火炮高低向系统式(10),考虑电机粘滞摩擦系数Ba,驱动系统粘性摩擦系数Bb,外界干扰d2具有不确定性。将以上不确定性参数Ba、Bb、d2分解为
(12)

将式(11)代入火炮稳定系统方位向模型式(6)中,将式(12)代入火炮稳定系统高低向模型式(10)中,得到全电驱动下带有不确定性的火炮稳定系统方位向与高低向系统动力学模型
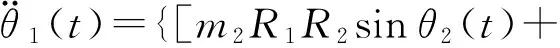
(13)

(14)
以上具有不确定性的坦克双向稳定系统动力学模型综合考虑了全电驱动下火炮稳定系统、执行机构(伺服电机与电动缸)、控制系统的非线性、耦合性与不确定性。接下来将以此动力学模型为基础,研究全电驱动下火炮双向稳定控制策略。
2 控制目标描述


定义跟踪误差:
(15)
将该跟踪误差作为控制器设计的控制对象,对θi(i=1,2)求两次微分,可得:
(16)

(17)
式中:
(18)
(19)
(20)
同理,可将高低向系统动力学模型转换为
(21)
式中:
(22)
(23)
(24)
(25)
(26)
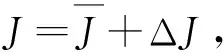
(27)
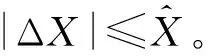
令σ1=[ΔJΔBmΔd1Δdt]T,将火炮方位向系统动力学模型(17)分解并重新整理得
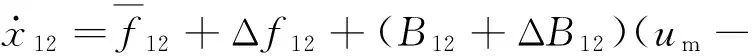
(28)

(29)
(30)
(31)
(32)
ΔB12=ktNΔX,
(33)
(34)
令σ2=[ΔBaΔBbΔd2]T,同理将火炮高低向系统动力学模型(21)分解并重新整理得

(35)

(36)
(37)
B22=M2p1,
(38)
(39)

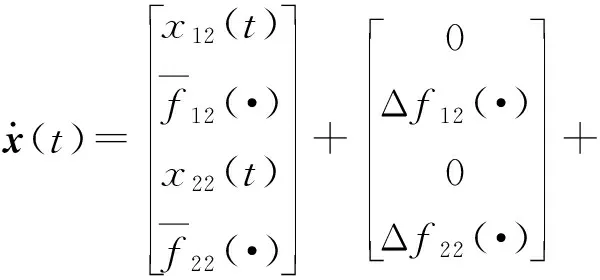
(40)
式中:x(t)∈R4为系统状态变量;um(t)∈R为伺服电机控制输入;uc(t)∈R为电动缸控制输入;σ(t)∈Σ⊂R7为系统不确定性参数(Σ⊂R7是未知但紧凑的集合,代表不确定性参数σ的界值)。该全电坦克火炮双向稳定系统状态空间模型将为研究全电驱动下火炮双向稳定控制提供模型基础,可看作受控系统或受控对象。
3 自适应鲁棒控制器设计
γi(0)=0,i=1,2,3,
(41)
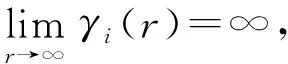
(42)
对于所有的(x,t)∈R2×R,
(43)
(44)
分析式(40),将不确定项Δf和ΔB分解为“确定”项与“不确定”项相乘的形式
Δf(x,σ,t)=B(x)h(x,σ,t),
(45)
ΔB(x,σ)=B(x)D(x,σ),
(46)
式中:B(x)为确定矩阵函数,h(x,σ,t)与D(x,σ)为不确定矩阵函数,其中

(47)
(48)

(49)
考虑其不确定性,令
(50)
由此,式(49)可重新整理为
(51)
式中:
(52)
(53)
针对不确定性综合表征参数α,设计如下自适应鲁棒控制器
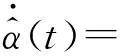
(54)
式中:αi(t0)>0(αi是向量α的第i个元素,i=1,…,k);k1,2>0为常标量,代表自适应律的设计参数。
为了实现全电驱动下的火炮双向目标跟踪控制,设计如下自适应鲁棒控制器
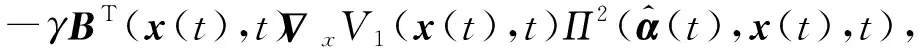
(55)
式中,γ>0为设计参数。
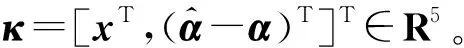

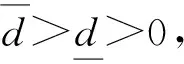
选择李雅普诺夫备选函数为
(56)
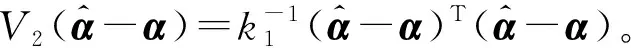
对于受控系统式(40),李雅普诺夫导函数为
(57)
根据式(44)~(46),可得
(58)
根据式(54)和(55),可得
(59)

(60)
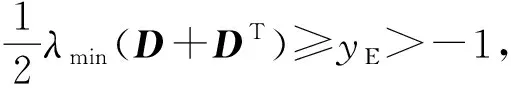
(61)
由此,式(60)中
(62)
将其代入式(60),可得
(63)
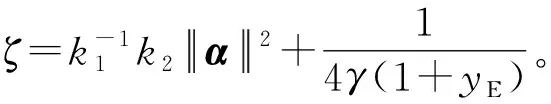
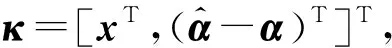
(64)
联合式(63),可得
(65)
基于以上分析,根据文献[23-25],系统实用稳定性成立,具体如下:
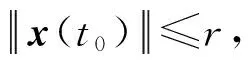
(66)
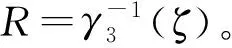
(67)


经过以上分析,当控制器u施加在受控系统式(40)上时,可使系统呈现预期的一致有界性、一致最终有界性与一致稳定性。
4 仿真与分析

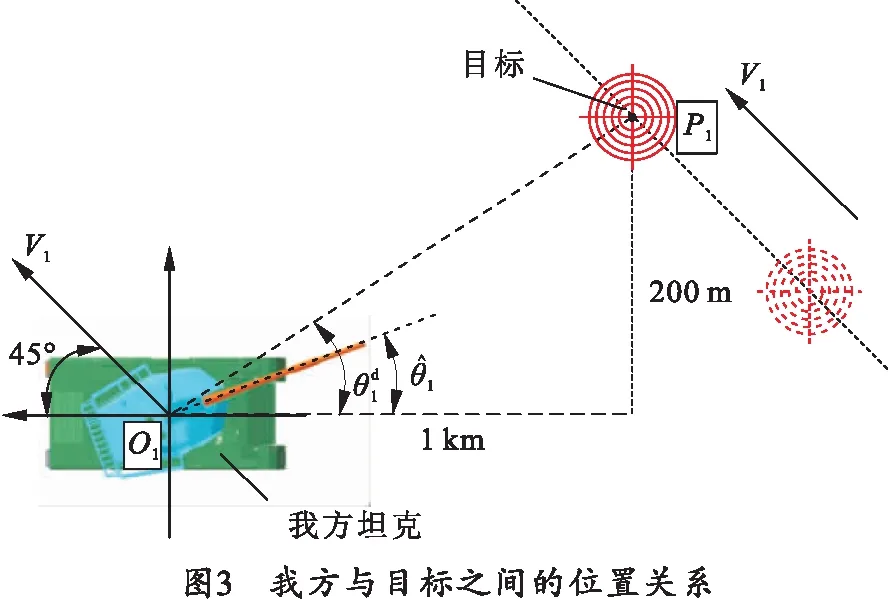
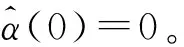
考虑系统中存在的不确定性扰动,通过计算机生成随机数模拟自身传动误差力矩、外界干扰力矩,形成幅值为5 kN·m的力矩扰动;针对系统中存在参数摄动问题,选取:电机转动惯量J=0.021+0.002 1sin 10t,kg·m2;粘滞阻尼系数Bm=0.008 8+0.000 88sin 10t,N·m·s/rad;粘滞摩擦系数Ba=0.015 3+0.001 53sin 10t,N·m·s/rad;驱动系统粘性摩擦系数Bb=0.006 3+0.000 63·sin 10t,N·m·s/rad。
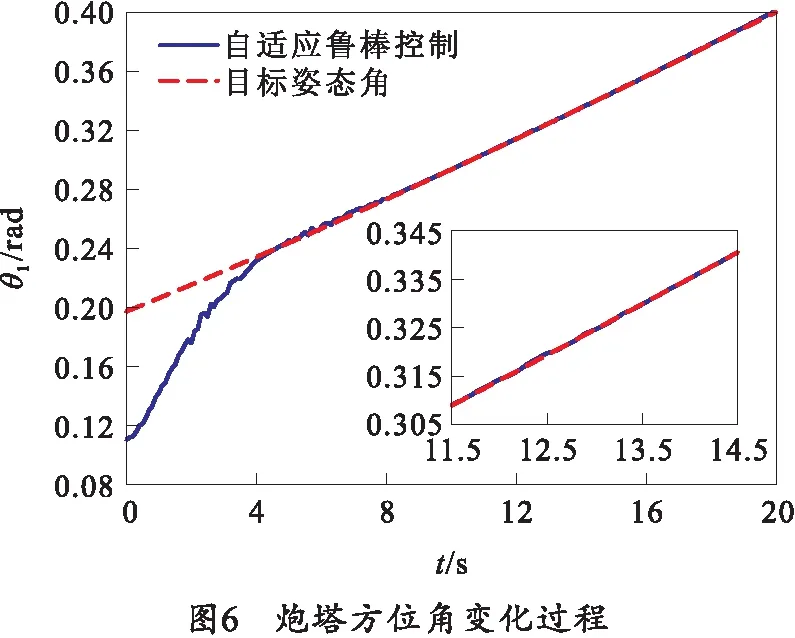
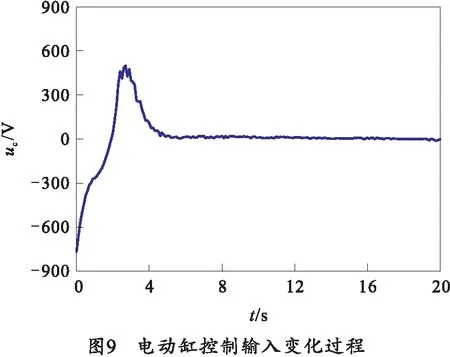
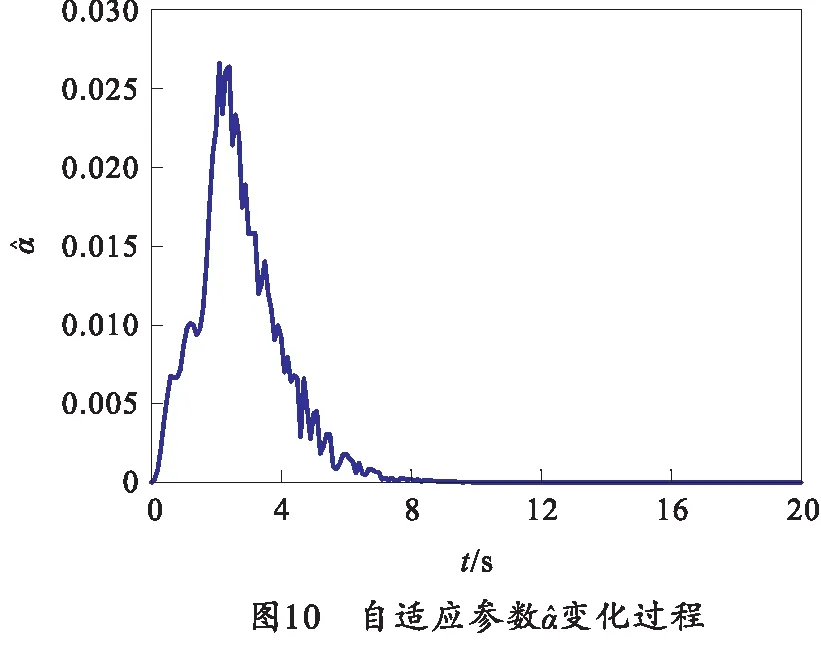
仿真结果如图4~10所示。其中,图4和图5分别为方位向跟踪误差e1和高低向跟踪误差e2动态对比图。由仿真结果来看,在所提自适应鲁棒控制器作用下,方位向跟踪误差e1和高低向跟踪误差e2在4 s后收敛并稳定在零附近,充分验证本文的控制方法对复杂时变不确定性的抑制效果。




5 结论
笔者针对坦克火炮双向稳定系统这一不确定性机械系统,将火炮行进间动态目标追踪问题转化成双向角度控制问题,设计自适应鲁棒控制器,在多种复杂时变不确定性干扰下,系统具有良好的动态跟踪特性,主要贡献如下:
1)分析火炮稳定系统工作原理,研究该非线性系统动力学特性,利用拉格朗日建模方法构建综合了方位向和高低向稳定系统解析动力学模型,该模型具有较强的真实性和实用性。
2)研究火炮稳定系统执行机构动力学模型,并考虑系统不确定性,构建考虑执行机构与不确定性的双向稳定系统解析动力学模型,基于此模型所设计的控制器可充分抑制系统的非线性、不确定性与耦合性等影响。
3)所设计的自适应鲁棒控制策略能较好地抑制系统建模误差、外界干扰等复杂不确定性的影响,使坦克火炮能够稳定地跟踪移动目标。
