磁轨关系建模对高速磁浮动力学仿真的影响

王志宇，马卫华*,，罗世辉，王波，王爱彬,2，张晓旭

磁轨关系建模对高速磁浮动力学仿真的影响

王志宇1，马卫华*,1，罗世辉1，王波1，王爱彬1,2，张晓旭1

（1.西南交通大学 牵引动力国家重点实验室，四川 成都 610031；2.中车长春轨道客车股份有限公司，吉林 长春 130113）

为研究磁轨关系建模方式对高速磁浮列车动力学仿真的影响，本文首先建立将磁轨关系简化为2、4、12三种等效集中力数量的单电磁铁模型，计算单电磁铁模型在正弦轨道不平顺下受到的悬浮力，得到不同相位、不同角频率的轨道不平顺激扰对悬浮力的影响。其次通过修正后的德国高速低干扰谱设置轨道不平顺，对比分析不同单电磁铁模型的悬浮力变化；并建立高速磁浮列车动力学模型，通过动力学仿真计算得到列车车体与摆杆间接口的垂向载荷数据，最后通过雨流计数法得到接口载荷幅值数据并进行分析。研究结果表明：等效集中力数量对仿真计算中第1位摆杆接口载荷的影响较大，随着等效集中力数量的增加，所得载荷数据中大幅值循环占比逐渐减小，小幅值循环占比逐渐增大。在低速时等效集中力数量对于仿真结果的影响较为显著，而在时速600 km时影响较小。

磁浮列车；动力学模型；磁轨关系；接口载荷

磁浮列车凭借无磨耗、环境友好、速度域广、乘坐舒适性高等优点，成为轨道交通的一大发展方向。高速磁浮列车时速可达600 km，在长大干线运输中具有较强竞争优势[1-2]。随着国家对高速磁浮技术研发的统筹布局，为进一步对高速磁浮列车进行结构优化设计，需要得到列车各构件间的接口载荷数据。由于线路及相关技术成本限制，采用试验方式的难度较大。在动力学仿真中，通过建立列车动力学模型、设置外部激励，即可得到列车内部各接口的载荷时间历程数据。因此，基于计算机虚拟环境的CAE仿真也是获得列车接口载荷的有效手段之一[3]。学者们对使用计算机仿真模拟实际工况做了大量研究，李岑等[4]建立磁浮列车动力学模型，通过动力学计算得到悬浮模块各作用位置的载荷时间历程，将载荷数据作为输入条件，可用于悬浮架疲劳寿命计算；FENG等[5]通过动力学仿真分析高速磁浮摆杆长度对列车动力学响应的影响，并给出了选取建议；ZHAI等[6]通过有限元仿真计算了不同负载工况下的磁铁受力特性，并通过与线路试验数据对比验证了仿真数据的可靠性；LI等[7]建立了考虑轨道、桥梁柔性的车轨桥耦合动力学模型，对比分析了仿真模型与实际模型的动力学特性。

不同于轮轨高铁列车通过轮轨接触点承载车体质量，高速磁浮列车利用通电导体产生磁场，通过磁场吸力及主动控制保持额定的小间隙（8～10mm），将列车质量均匀施加于线路，属于分布载荷[8]。电磁铁与导轨相互作用关系即磁轨关系是进行磁浮列车系统动力学研究的基础，磁轨关系在本质上确定了磁浮列车系统的动力特性[9]。因此，学者们针对磁轨关系开展了大量研究，BRZEZINA等[10]利用保角变换推导出垂向和横向电磁力的解析公式；CHEN等[11]建立柔性梁和单电磁铁模型，使用单个集中力表示磁轨关系，分析控制算法的控制精度和系统鲁棒性；王波等[12]分别采用弹簧阻尼法和悬浮控制法建立了磁轨关系模型，对比分析了两种磁轨关系的力学特性；魏高恒等[13]以1力元、3力元、5力元模拟单电磁铁悬浮力，分析比较了不同力元模拟的电磁铁悬浮力与实际悬浮力之间的差异；赵春发等[14]分析了不同等效集中力数量下，车体加速度及简支梁跨中挠度的时间历程曲线；汪科任等[15]将电磁铁悬浮力简化为悬浮架两端的2个集中力，分析了二系悬挂中置与端置的磁浮列车振动特性。在磁轨关系的处理中，由于计算机求解能力的限制，需要将连续模型问题转换为离散形式的问题，即将磁轨相互作用的分布载荷转换为相应的集中载荷。而在现有研究中，关于集中载荷的集中力数量对动力学仿真中列车接口载荷的影响的相关研究较少。

本文选取高速磁浮列车为研究对象，通过不同数量的等效集中力表述磁轨关系，建立以2点、4点、12点支撑的悬浮模块为基础的高速磁浮列车模型，对比分析不同等效集中力数量下高速磁浮列车动力学仿真中垂向接口载荷的变化，以给出磁轨关系等效集中力数量的选取建议，为通过动力学仿真获取高速磁浮列车关键位置的载荷时间历程数据提供相应参考。

1 列车系统结构

1.1 列车结构

高速磁浮列车结构及结构序号如图1所示，列车主要由车体、二系悬挂、悬浮架、悬浮电磁铁、导向电磁铁等结构组成，从列车1位端到2位端方向从小到大依次定义摆杆顺序号。每节车包含4个悬浮架，每个悬浮架由2个C型悬浮弓组成。

磁浮列车垂向载荷相关各部件的拓扑关系如图2所示，悬浮电磁铁通过一系悬挂安装在相邻的C型悬浮弓上，左右摇枕通过防侧滚橡胶耦合在一起，并通过摆杆与空气弹簧组成二系悬挂，连接悬浮架与车体。列车的垂向力传导路径依次为悬浮电磁铁、悬浮架、空气弹簧、摇枕、摆杆、车体。

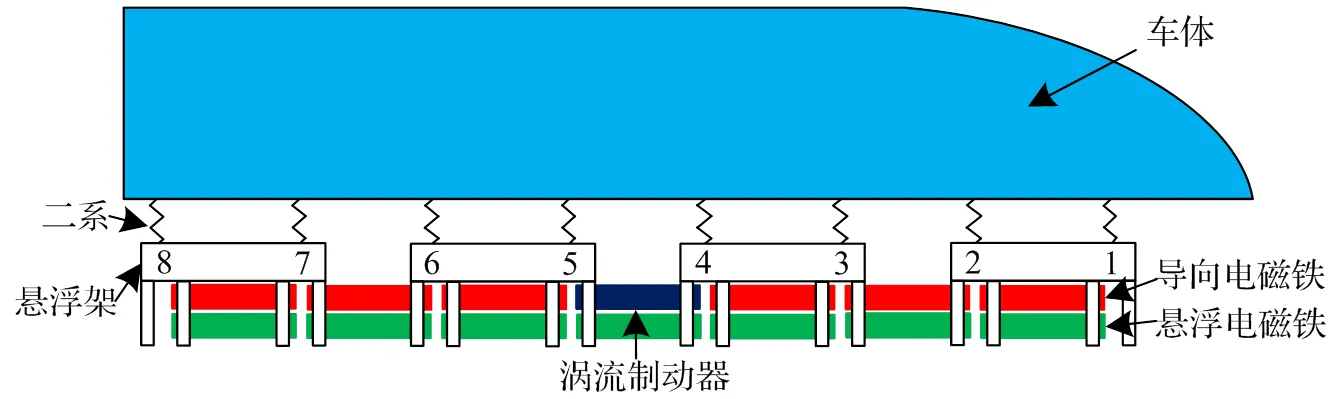
图1 高速磁浮结构示意图

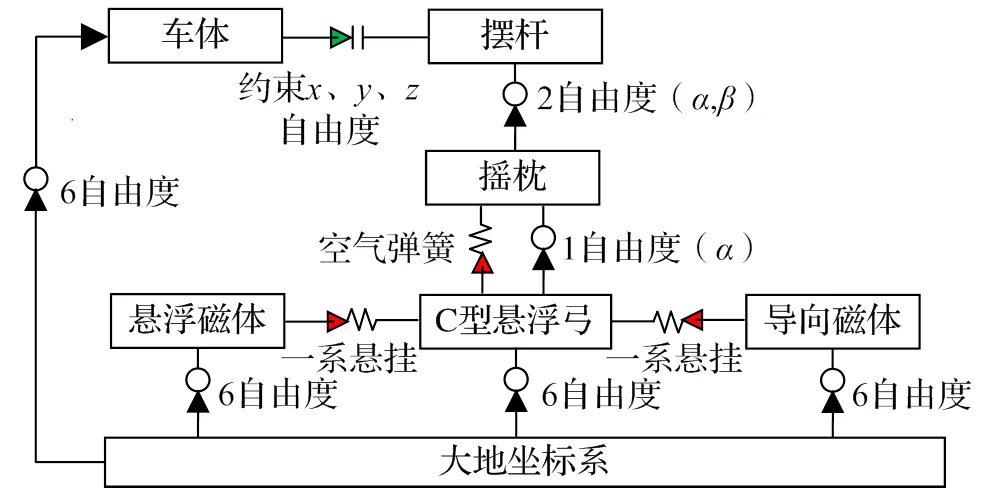
图2 高速磁浮拓扑关系示意图

1.2 悬浮控制系统模型

将搭接在悬浮弓之间的整个悬浮电磁铁作为单个悬浮模块，其磁轨关系如图3所示。根据牛顿第二定律及电磁学原理可得公式：

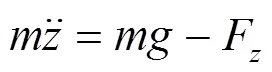
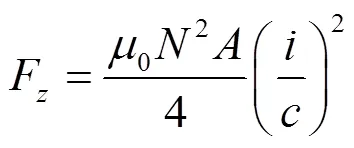
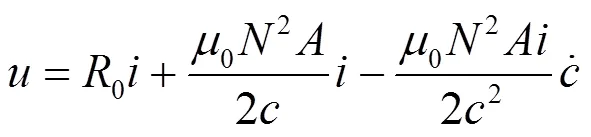
式中：为电磁铁质量；为垂向位移；F为单电磁铁所受悬浮力；0为真空磁导率；为线圈匝数；为磁极面积；为电磁铁电流；为悬浮间隙；为电磁铁电压；0为线圈电阻。

悬浮力与间隙及电流的关系如式（2）所示，悬浮力与间隙的平方成反比，与电流的平方成正比。在平衡点处，微小的扰动即可使系统离开平衡状态。因此，需要设计悬浮控制模型，调整悬浮电磁铁电流，使列车在轨道激扰下保持稳定运行。

如图3所示，高速磁浮列车通过在悬浮模块两端安装间隙传感器及加速度传感器，得到对应位置的间隙信号及加速度信号，并通过设计状态观测器得到速度信号。

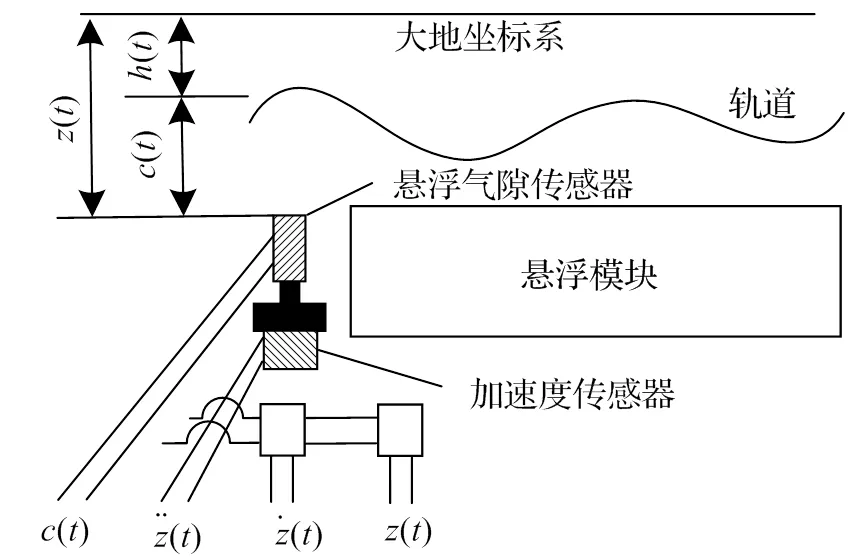
图3 磁轨关系示意图

模型中使用的位置－速度－加速度反馈控制的计算公式为：

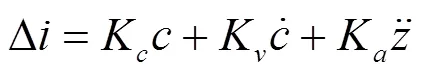
式中：Δ为电流变化量；K为间隙反馈系数；K为速度反馈系数；K为加速度反馈系数。

2 磁轨关系简化建模

实际磁轨关系模型较为复杂，建立完整的磁轨关系模型虽然可以提高仿真精度，但会显著降低计算速度，不适合直接应用于动力学计算中。因此，在动力学模型中模拟磁轨关系时，需要对模型进行一定程度的简化。高速磁浮列车结构复杂，系统总自由度较高，因此高速磁浮对列车模型，尤其是磁轨关系模型的建立有着更高的要求。所以，如何在结构简化过程中保证磁轨相互作用的力学特性与实际接近，是高速磁浮列车建模中较为重要的一环。在建立高速磁浮列车动力学模型之前，有必要对磁轨关系的建模方式进行分析。

2.1 磁轨关系简化方式

单个悬浮模块的受力情况如图4所示。悬浮模块与轨道之间的电磁力分布在整个悬浮模块上，悬浮模块与轨道基准面的额定间隙为0＝10 mm。设纵向为方向，由于作用在悬浮电磁铁下的悬浮力为分布力，悬浮模块受到的悬浮力合力为磁轨作用面上分布力的积分。

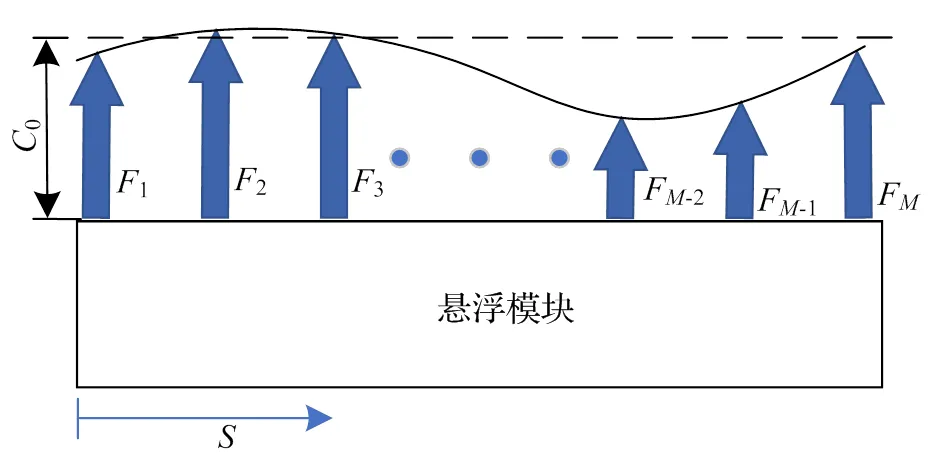
图4 悬浮模块受力情况

由于电磁力与悬浮间隙的平方呈反比，悬浮力不会在纵向上均匀分布。因此，设悬浮模块在微元d长度上所受悬浮力为dF，单个悬浮模块受到的悬浮力合力为F，可得到：

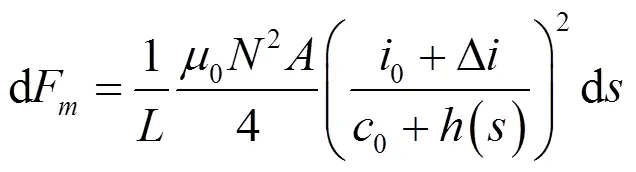
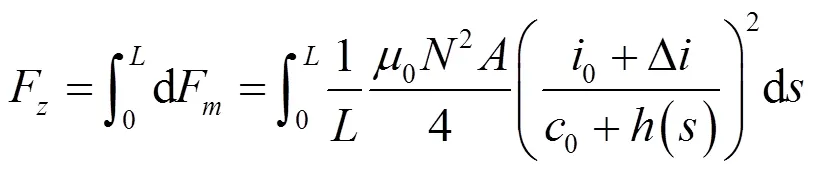
式中：为等效集中力元的纵向坐标；为单个悬浮模块长度；()为轨道不平顺。

在建立动力学模型时，通过将分布力简化为一定数量的集中力，完成对磁轨关系的简化。由于轨道不平顺的设置，悬浮模块在不同位置受到的电磁力不同，每个悬浮模块均受到相应力矩作用。若采用单力元模拟磁轨关系，集中力作用于悬浮模块中心位置，则在一定轨道不平顺激扰下，悬浮模块仅显示力的激扰，忽略了对悬浮模块的力矩输入，因此，模拟悬浮模块的磁轨相互作用，需要采用两个及以上集中力元才能反映出力矩对悬浮电磁铁的影响。本文分别取集中力数量为2、4、12。

将式（5）（6）简化得到：

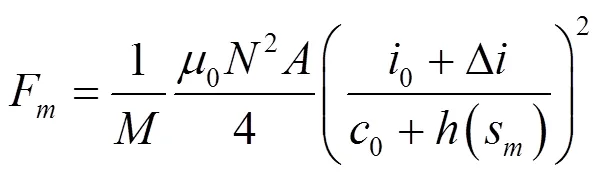
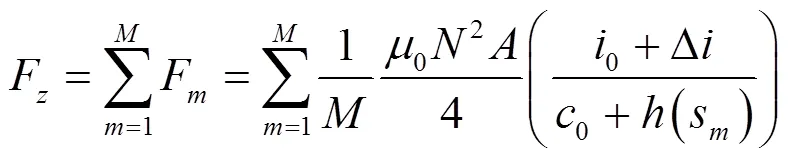
式中：F为悬浮模块在第个等效集中力点所受悬浮力；s为第点的纵向坐标。

2.2 不同磁轨作用模型理论分析

如图5所示，本文首先探究等效集中力的选取数量对磁轨相互作用力的影响，将悬浮模块水平放置，悬浮模块与系统坐标系距离为额定间隙0，引入轨道不平顺()＝sin()，为轨道不平顺变化幅值，为角频率。

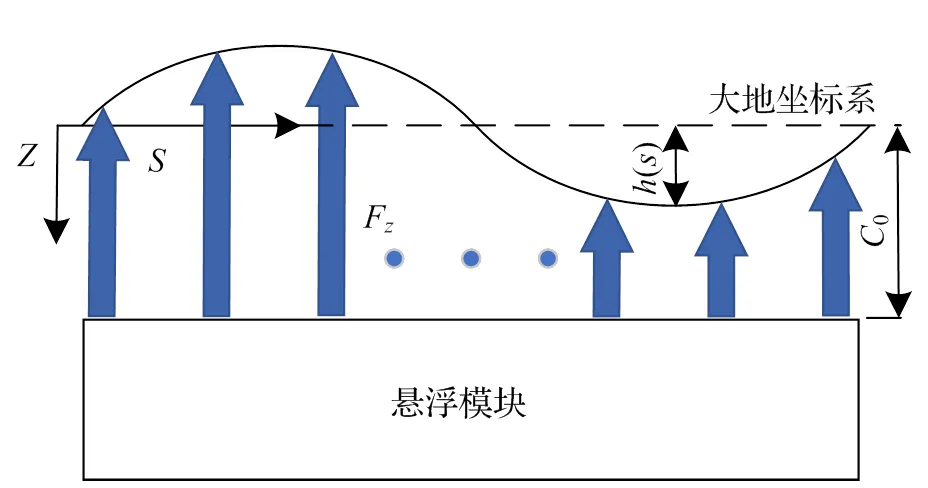
图5 悬浮模块受力示意图

在额定电流及额定悬浮间隙下，当为0时，悬浮模块受力为0，通过调节角频率，得到＝1 mm时，不同等效集中力数量下，悬浮模块悬浮力与0的比值，图6为＝200时不同频率、不同初始相位下，悬浮力与0的比值的变化。

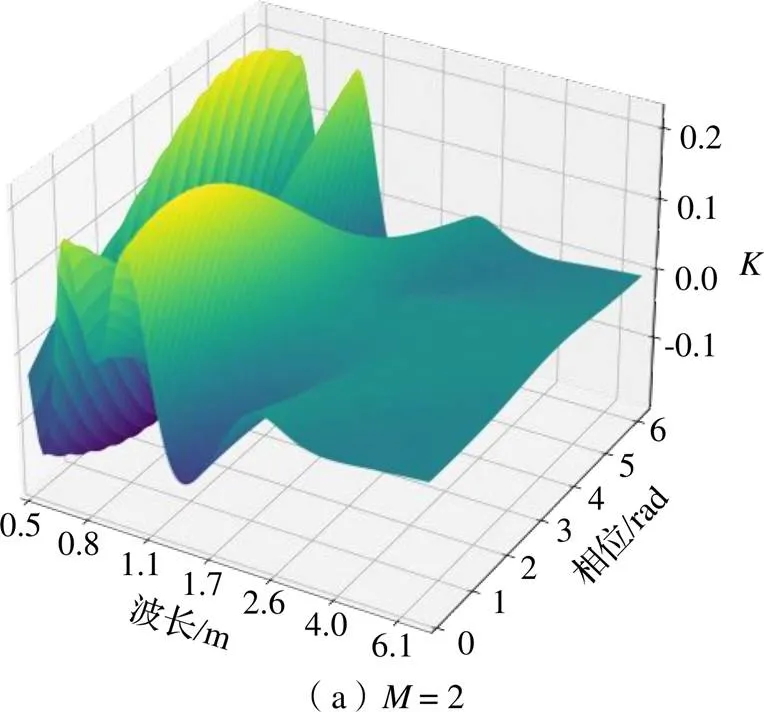
图7为＝2、4、12时不同波长及初始相位下悬浮力与取200时的差值。当等效集中力数量取较大值，即＝200时，随着波长的增大，悬浮力变化的最大值与最小值逐渐增大。短波不平顺初始相位对于悬浮力的影响远小于长波不平顺初始相位对悬浮力的影响。当取2、4、12时，若轨道不平顺波长较短，轨道不平顺相位与波长的变化均能引起悬浮力的剧烈变化，随着波长的增加，不同模型间的悬浮力差异逐渐减小。且各模型悬浮力相对变化范围与等效集中力数量呈负相关趋势，等效集中力数量越多，悬浮力相对变化越小。

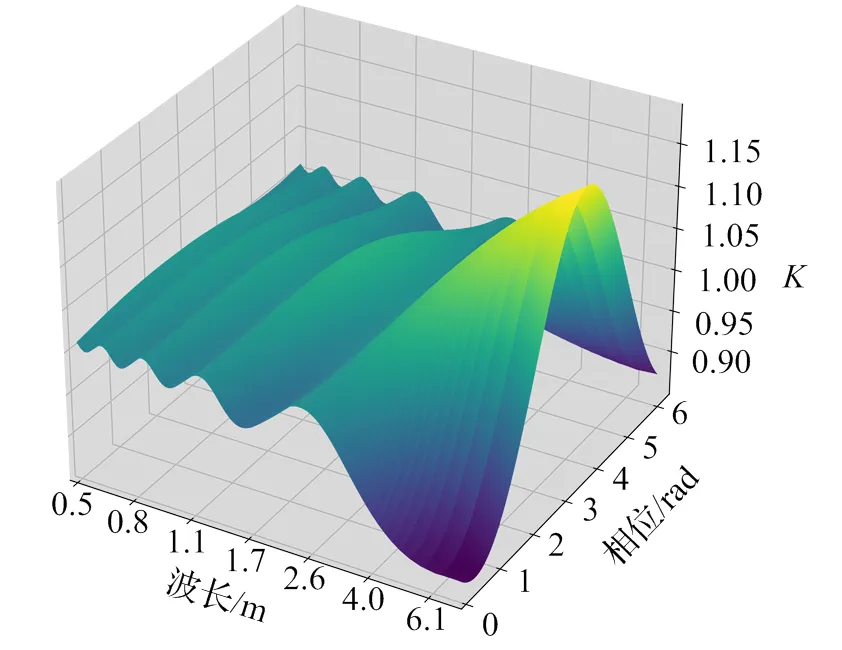
图6 悬浮力变化示意图（M＝200）

在实际轨道谱中，轨道不平顺由不同频率的不平顺叠加而成。以德国高速低干扰谱为例，通过轨道谱计算得到的轨道不平顺以长波不平顺为主。因此，为进一步分析不同等效集中力数量模型在实际轨道不平顺下的悬浮力变化，通过修正后的德国高速低干扰谱定义了轨道不平顺。在10 mm额定悬浮间隙下，同样只赋予悬浮电磁铁纵向自由度，得到不同纵向位置的轨道不平顺变化及不同等效集中力数量下的悬浮力变化如图8所示。随着等效集中力数量的增加，悬浮力变化趋势更加平滑，不同模型间悬浮模块受到的悬浮力差异主要体现在轨道不平顺变化极值处；与＝200相比，等效集中力数量＝2时悬浮力波动较大，随着的增加则悬浮力波动变化减小，当＝12时悬浮力变化与＝200时基本相同。

3 动力学仿真

3.1 高速磁浮动力学模型

在多体动力学软件中建立高速磁浮动力学模型，模型主要包括车体、悬浮架两大部分，如图9所示。本文重点讨论高速磁浮车体与走行机构接口处垂向载荷的变化趋势，即取车体摆杆座处的接口载荷数据进行分析。

3.2 摆杆垂向力分析

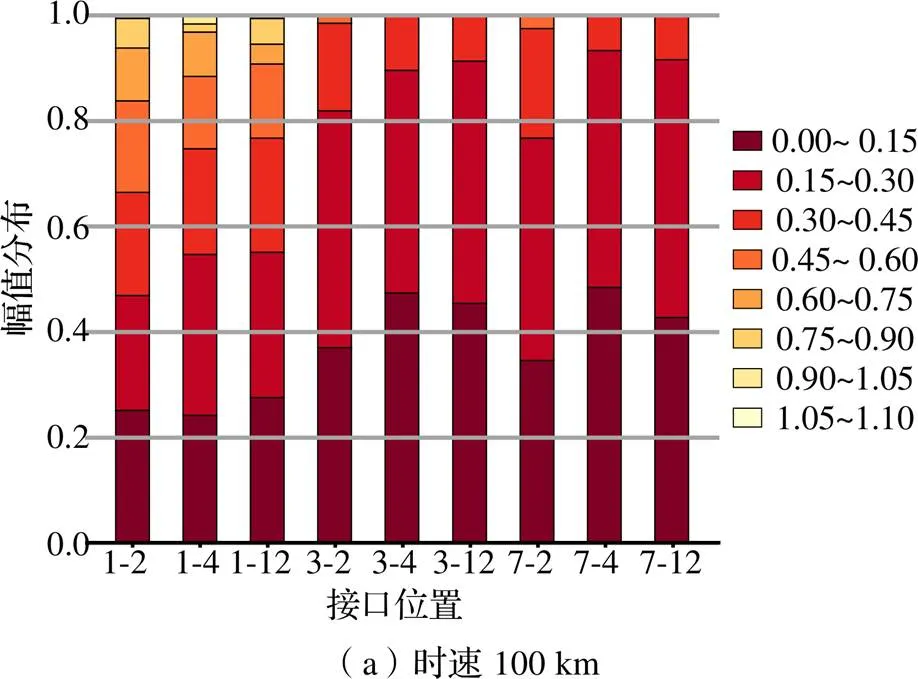
设置修正后的不平顺幅值后的德国高速低干扰谱作为轨道不平顺，建立不同等效集中力数量的高速磁浮列车动力学模型进行仿真计算。通过雨流计数法对仿真得到的摆杆处载荷进行计数处理，并通过雨流过滤方法滤除小循环，得到摆杆垂向载荷幅值数据分布如图10所示，图中，横向坐标为磁轨关系等效集中力数量分别取2、4、12时列车与1、3、7位摆杆相铰接的接口位置示意，纵坐标为不同幅值范围的载荷循环所占总体载荷循环数量的比重、不同颜色代表不同幅值的载荷循环。

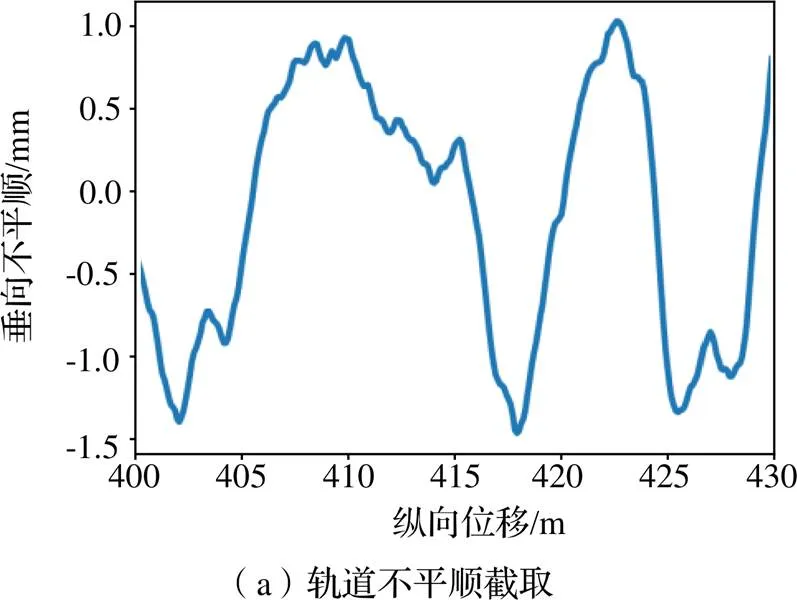
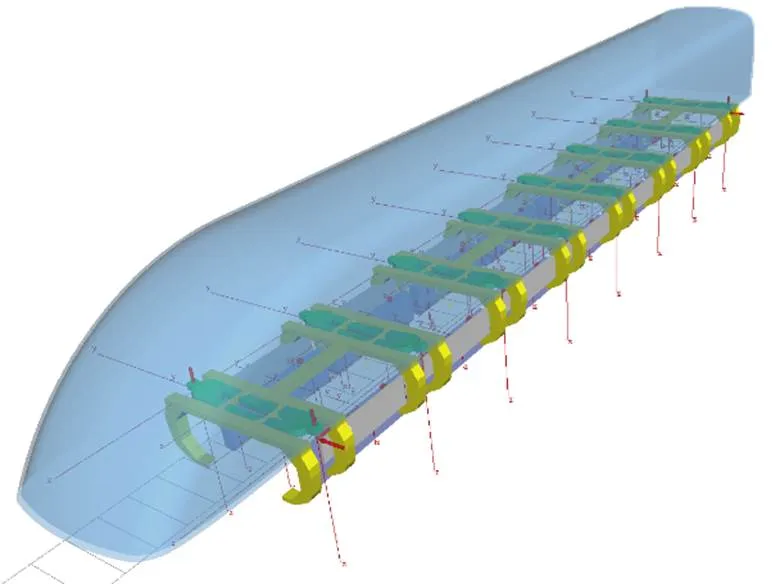
图9 动力学模型示意图

不同模型中，第1位摆杆接口载荷的幅值数据远大于第3位及第7位摆杆接口载荷；在时速100 km和时速300 km时，随着的增加，第1位摆杆接口载荷大幅值循环占比逐步降低，小幅值循环占比逐步提高；在时速600 km时，不同模型的接口载荷循环幅值分布没有较明显差异；相对于第1位摆杆接口载荷，第3位及第7位摆杆接口载荷随着的改变没有表现出较强的规律性变化。因此，在低速域仿真时，动力学模型中的磁轨关系等效集中力数量对于列车头部接口的仿真结果影响较大，随着列车速度的增加，等效集中力数量对于仿真结果的影响比重逐渐减小。

4 结论

（1）在单自由度悬浮模块模型中，计算电磁铁在不同初始相位、波长的不平顺激励下的悬浮力。在短波不平顺下，不平顺初始相位及波长对于悬浮力的影响较大，而随着等效集中力数量的增加，悬浮力变化范围减小；

（2）将轨道不平顺设置为修正后的德国高速低干扰谱，在单自由度悬浮模块模型中，额定电流下不同等效集中力数量对于悬浮模块垂向力的影响较小，不同模型悬浮力的差异主要集中在轨道不平顺变化的极值处；

（3）整车动力学模型中，第1位摆杆接口垂向载荷幅值远大于第3位及第7位摆杆接口载荷。时速100 km及300 km时仿真得到的第1位摆杆接口载荷幅值循环分布受等效集中力数量影响较大；时速600 km时不同模型间载荷数据差异较小，第3位及第7位摆杆接口载荷幅值循环分布受等效集中力数量影响较小；

（4）针对磁浮列车磁轨关系的简化建模，列车速度较低时可适当提高磁轨关系等效集中力的数量，以获得更为准确的载荷数据；列车速度较高时等效集中力数量对载荷数据的影响能力下降，可减少磁轨关系等效集中力数量。

[1]THORNTON. Efficientand affordable maglev opportunities in the United States[J]. Proceedings of the IEEE，2009，97（11）：1901-1921.

[2]李京文，宗刚. 高速磁浮交通系统在长达干线的适用性研究[M]. 北京：知识产权出版社，2014：1-10.

[3]王春山，王曦，杨广雪. 铁路货车载荷谱及应用[M]. 北京：中国铁道出版社，2018：221-235.

[4]李岑，姚毓瑾，虞大联，等. 基于动力学仿真分析的磁悬浮列车悬浮架载荷特征研究[J]. 北京交通大学学报，2021，45（3）：118-125.

[5]FENG Yang，ZHAO Chunfa，LIANG Xin，et al. Influence of bolster-hanger length on the dynamic performance of high-speed EMS maglev vehicles[J]. Vehicle System Dynamics，2022，60（11）：3743-3764.

[6]ZHAI Mingda，LONG Zhiqiang，LI Xiaolong. Calculation and evaluation of load performance of magnetic levitation system in medium-low speed maglev train[J]. International Journal of Applied Electromagnetics and Mechanics，2019，61（4）：1-18.

[7]LI Miao，LUO Shihui，MA Weihua，et al. Experimental and numerical investigations of the dynamic responses of low and medium speed maglev train-track-bridge coupled system[J]. Vehicle System Dynamics，2022，60（5）：1555-1578.

[8]徐飞，罗世辉，邓自刚. 磁悬浮轨道交通关键技术及全速度域应用研究[J]. 铁道学报，2019，41（3）：40-49.

[9]翟婉明，赵春发. 磁浮车辆/轨道系统动力学（Ⅰ）——磁/轨相互作用及稳定性[J]. 机械工程学报，2005，41（7）：1-10.

[10]BRZEZINA W，LANGERHOLC J. Lift and side forces on rectangular pole pieces in two dimensions[J]. Journal of Applied Physics，1974，45（4）：1869.

[11]CHEN Chen，XU Junqi，LIN Guobin，et al. Model identification and nonlinear adaptive control of suspension system of high-speed maglev train[J]. Vehicle System Dynamics，2022，60（3）：884-905.

[12]王波，罗世辉，汪科任，等. 不同磁轨关系对中低速磁浮车辆垂向动力学性能的影响[J]. 机车电传动，2019（5）：82-86.

[13]魏高恒，陈晓昊，罗世辉，等. 轨道高低不平顺对磁浮车辆动力学性能的影响[J]. 机车电传动，2019（4）：56-60，66.

[14]赵春发，翟婉明，蔡成标. 磁浮车辆/高架桥垂向耦合动力学研究[J]. 铁道学报，2001，23（5）：27-33.

[15]汪科任，罗世辉，马卫华，等. 磁浮列车静悬浮车轨耦合振动对比分析[J]. 西南交通大学学报，2020，55（2）：282-289.

Influence of Magnet-Track Interaction Modeling on DynamicSimulation of High-Speed Maglev Vehicles

WANG Zhiyu1，MA Weihua1，LUO Shihui1，WANG Bo1，WANG Aibin1,2，ZHANG Xiaoxu1

( 1.State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031,China; 2.CRRC Changchun Railway Vehicles Co.,Ltd.,Changchun 130113,China )

This paper is to study the influence of the magnet-track interaction modeling method on the dynamic simulation of high-speed maglev vehicles. Firstly, the magnet-track interaction is simplified to three models with the equivalent point force of 2, 4 and 12 to calculate the suspension force distribution of different single electromagnet models under sine track irregularity, and the influence of track irregularity with different phases and different angular frequencies on the suspension force is obtained. Secondly, the track irregularity is set through the revised German high-speed low interference spectrum, and the suspension force change of different single electromagnet models is analyzed. Thirdly, the dynamic model of the high-speed maglev vehicle is established to obtain the vertical load data of the interface between the vehicle body and the swing rods through dynamic simulation calculation. Finally, the vertical load data derived through the rain flow counting method is analyzed. The result show that the amount of equivalent point force mainly affects the load of the 1st swing rod. As the amount of equivalent point force increases, in the load data derived, the proportion of the cycles with larger amplitude increases, and the proportion of the cycles with smaller amplitude decreases. At low speeds, the amount of the equivalent point force has a significant impact on the simulation results, but at the speed of 600 km/h, the impact is relatively small.

maglev vehicles；dynamic models；magnet-track interaction；interface load

U292.9

A

10.3969/j.issn.1006-0316.2023.07.005

1006-0316 (2023) 07-0031-07

2022-09-16

王志宇（1997－），男，山东菏泽人，硕士研究生，主要研究方向为磁浮列车动力学，E-mail：123816348@qq.com。*通讯作者：马卫华（1979－），男，山东滕州人，博士，研究员，主要研究方向为磁浮列车悬浮架设计，E-mail：mwh@swjtu.edu.cn。