基于断齿故障下的斜齿轮副动态性能研究

闫春爱，刘明勇，邓恩喜，韩新光

基于断齿故障下的斜齿轮副动态性能研究

闫春爱1，刘明勇*,2，邓恩喜2，韩新光2

（1.武昌工学院 智能制造学院，湖北 武汉 430065； 2.湖北工业大学 湖北省农机装备智能化工程技术研究中心，湖北 武汉 430068）

为了探究断齿故障因素对齿轮传动系统的动态特性，通过势能法，考虑赫兹、弯曲、剪切及轴向压缩，结合切片法，研究齿轮时变啮合刚度的影响规律。综合考虑齿轮时变啮合刚度、时变啮合阻尼、静态传递误差及摩擦激励等因素，基于斜齿轮动力学模型，采用Runge-Kutta法求解，研究了故障参数对系统动力学特性的影响。结果表明，含断齿故障的齿轮综合有效啮合刚度有较大幅度的减小，系统中的动态传递误差、振动速度及振动加速度出现周期性冲击现象，频域响应出现了以啮合频率为中心的边频信号，研究结果可有效实现断齿齿轮传动故障的识别。

断齿故障；啮合刚度；动力学模型；周期性

齿轮系统常在高转速、高温度、承载恶劣等复杂使役环境下运行。在封闭的齿轮箱中，断齿故障是齿轮传动中最常见的故障之一，不易被发现，断齿故障的发生会严重影响机械传动系统的可靠运行和安全性，造成齿轮的疲劳寿命降低，影响设备的性能和使用，甚至会造成严重的机械事故。齿轮副时变啮合刚度是进行齿轮系统动力学分析的重要参数，可较好地反映断齿故障下齿轮系统的振动特征情况。因此，研究断齿故障下齿轮动态特性规律是保障设备安全的重要手段之一。

时变啮合刚度常常作为齿轮传动系统动力学分析的输入条件，国内外学者对时变啮合刚度开展系列研究。林腾蛟等[1]对斜齿轮进行了研究，使用有限元法分析各种裂纹参数对其啮合的影响，结果表明，齿轮啮合刚度随裂纹的增大而减小；马锐等[2]建立了单对齿轮的理论模型，分析其裂纹形成因素和振动特性，得到了含裂纹齿轮的动力学特性；朱丽莎等[3]提出了基于切片思想及切片耦合理论的斜齿轮啮合刚度计算方法，并分析了斜齿轮时变啮合刚度；万国志等[4]提出一种考虑齿根圆与基圆不重合时的啮合刚度修正方法，并采用势能法求解齿轮时变啮合刚度；Saxena等[5]采用势能法求得直齿轮副的啮合刚度，研究了不同裂纹长度对齿轮转子系统模态特性频率响应特性的影响；刘文等[6]依据切片法和积分思想，提出齿轮基圆与齿根圆大小不一致的情况下的齿轮时变啮合刚度修正算法；Wang等[7]提出斜齿轮时变啮合刚度还应考虑齿轮的轴向弯曲刚度、轴向扭转刚度与轴向基体刚度；肖正明[8]针对含有裂纹的行星齿轮进行了分析，建立了系统的动力学模型并进行了仿真分析，结果表明，建立的模型精度较高。王彦刚等[9]分析了不同故障下齿轮的非线性特性，建立了齿轮系统的动力学模型并进行分析，可以有效地区分故障信号的大小。在齿轮断齿故障方面，强仕杰等[10]基于ISO刚度计算准则对任意断齿角度下斜齿轮副啮合刚度的求解；严作堂等[11]通过断齿信号分析，提取了断齿故障特征并确定断齿的严重性和数量；陈宝庆等[12]分析了啮合力的幅值随着断齿程度的增加而明显增加。

现有研究对齿轮的时变啮合刚度进行了很好的评价，但若能在封闭齿轮箱中综合考虑故障因素对系统的振动动态响应规律，将更有助于斜齿轮传动系统的振动特性研究。因此，本文在建立斜齿轮断齿三维模型下，研究断齿故障下齿轮副时变啮合刚度规律，基于Runge- Kutta法求解，分析断齿故障下不同动力学参数对传动系统动态特性的影响规律，对齿轮副啮合状态的故障预测具有重要的工程研究意义。

1 断齿故障下的斜齿轮建模及啮合刚度计算

考虑小齿轮上其中一个轮齿发生断裂，利用SolidWorks软件的参数化建模如图1所示。

图1 斜齿轮断齿三维模型

准确有效的时变啮合刚度计算方法是进行动力学分析的关键，考虑计算时变啮合刚度的关键是求出轮齿啮合时的弹性变形量。如图2所示，本文基于r＞r情况，考虑小齿轮其中一个轮齿断裂，将轮齿啮合等效为变截面梁，运用势能法得到齿轮的有效综合啮合刚度。图2中：x为齿根圆与基圆在齿高方向的距离；为截面的齿曲线上的点与基圆在齿高方向的距离；为啮合点与基圆在齿高方向的距离；0为基圆与齿根圆接触齿面上的圆弧半径；h为截面的齿曲线上的点与齿轮中心线之间的距离；为合点与齿轮中心线之间的距离；0为齿面上齿根圆与基圆之间的夹角；2为压力角；α为啮合点在齿根方向的切线与齿轮中心线之间的夹角；为截面的齿曲线上的点在齿根方向上的切点与齿根圆之间的夹角；F为啮合点中配合齿的剪切力；F为啮合点中配合齿的弯曲力；为啮合点中配合齿的作用合力。

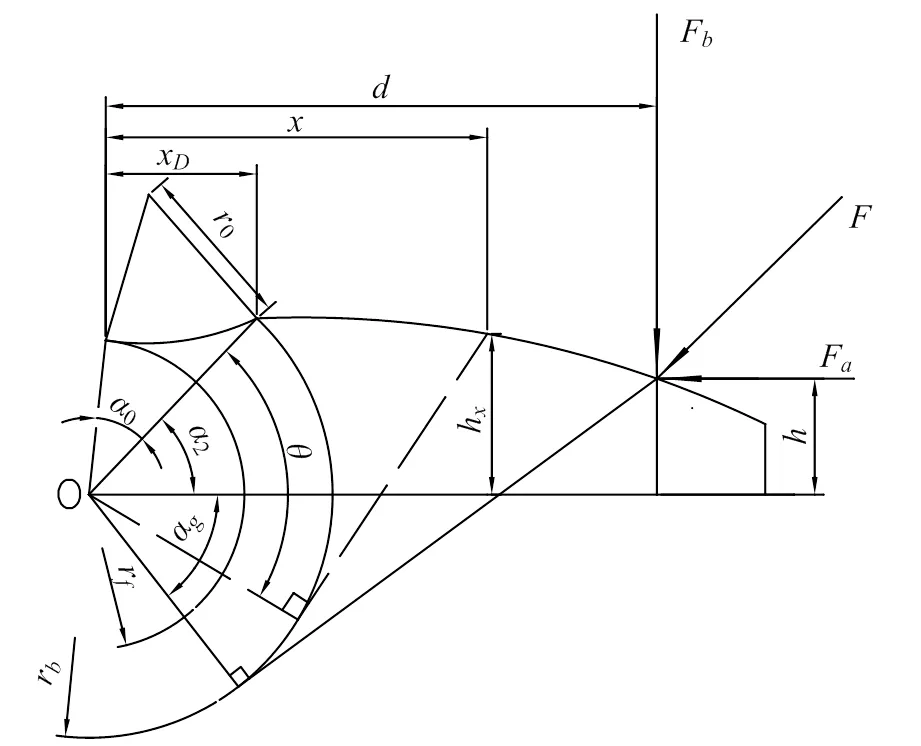
图2 接触齿对力学模型图

根据文献[13]中的弹性势能法，考虑齿轮啮合过程中的赫兹接触能、弯曲势能、剪切势能、轴向压缩能，计算断齿故障的综合啮合刚度。

根据能量法计算啮合齿轮储存的势能为：

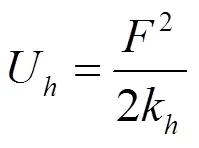
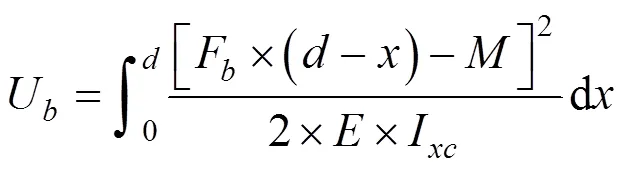
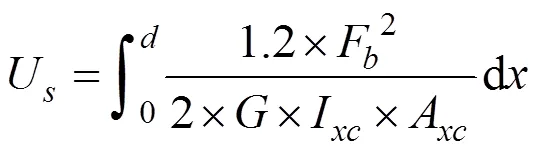
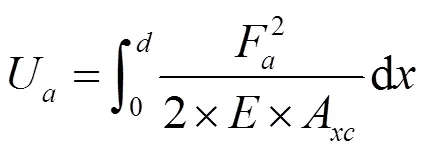
根据势能与刚度的关系可以得到：

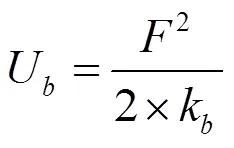
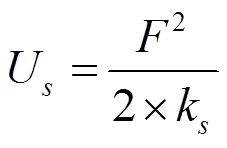
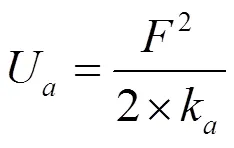
式中：U为赫兹刚度；U为弯曲势能；U为剪切能；U为轴向压缩能；k为赫兹刚度；k为弯曲刚度；k为剪切刚度；k为轴向刚度；I为有效面积惯性矩；A为有效横截面面积，；扭矩为F的弯曲效应。

得出齿轮的赫兹接触刚度为：

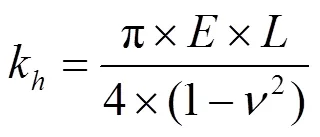
式中：为杨氏模量；为接触线长度；为泊松比。

齿轮的弯曲刚度如式（9）所示，剪切刚度如式（10）所示，压缩刚度如式（11）所示。

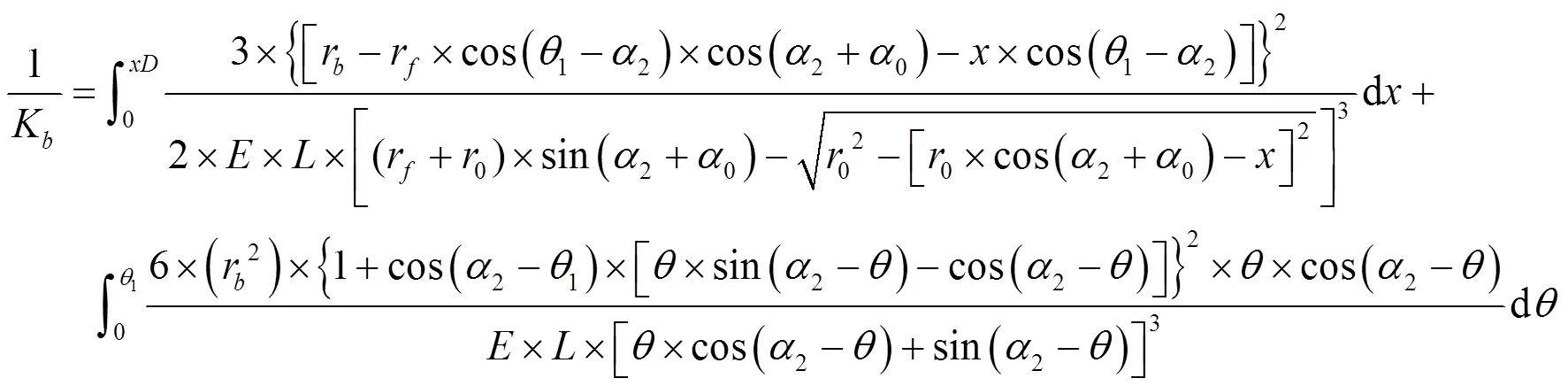
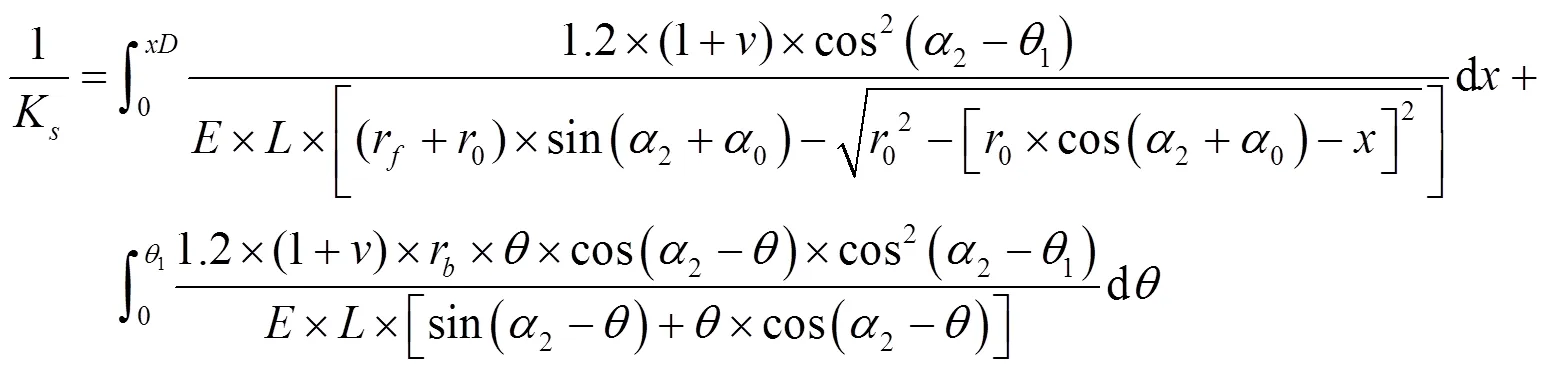
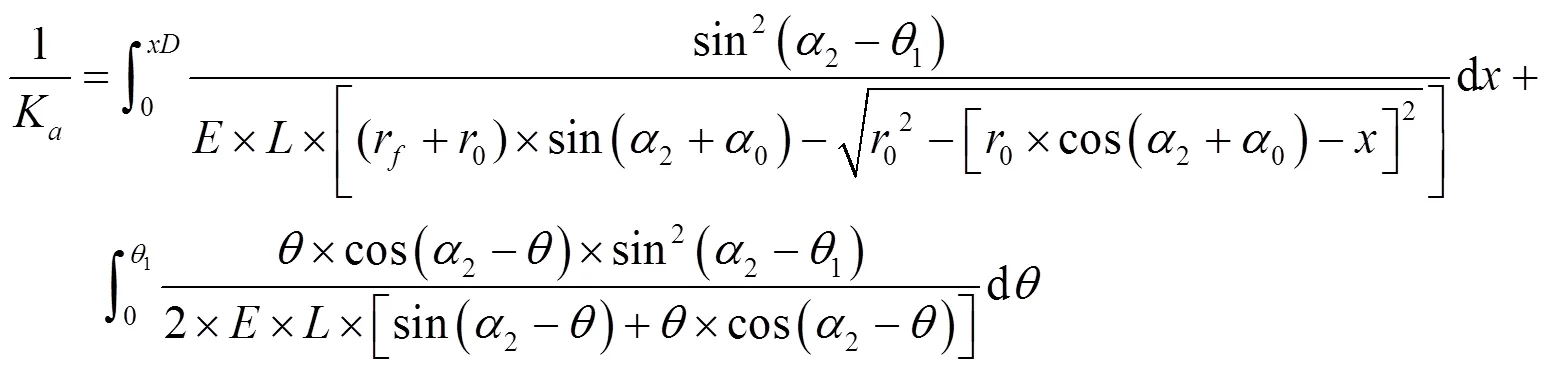
式中：1为啮合点在齿根方向上的切点与齿根圆之间的夹角。

根据式（8）～（11）得出综合啮合刚度为：

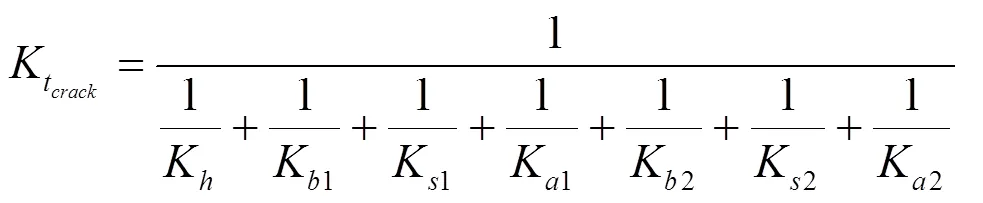
式中：下标1、2分别代表小齿轮和大齿轮。

如图1所示，小齿轮上其中一个轮齿发生断裂。若该轮齿未断裂，当它旋转到啮合区域时，它会与配合齿轮的大齿轮进行啮合。在双齿啮合区，断裂齿未发生接触，依旧为单齿啮合。因此，综合有效啮合刚度等价于单齿啮合刚度，综合有效啮合刚度为：

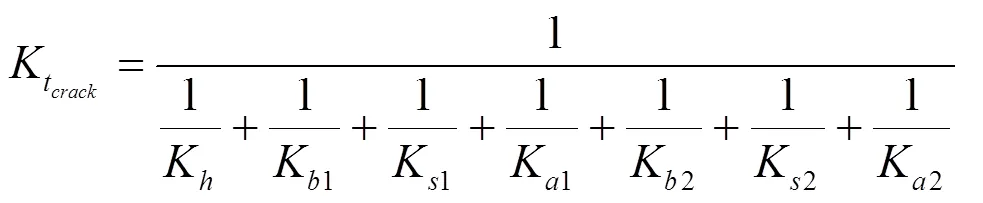
本文采用齿轮的参数如表1所示。

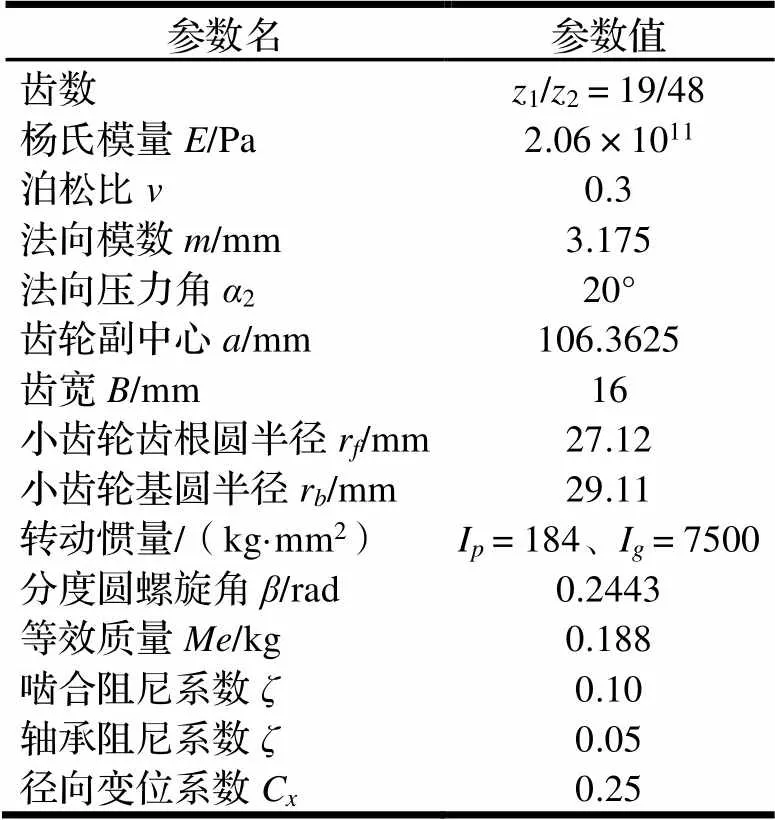
表1 齿轮几何模型基本参数

2 断齿对齿轮时变啮合刚度的影响

假设小齿轮为断齿故障齿轮，双齿啮合区发生单齿啮合，其综合啮合刚度如图3所示，可以得到，参与啮合的一对齿轮中其故障齿的啮合刚度比理想齿轮有较大幅度的降低。

齿轮进行周期性连续传动，采用切片法研究周期性时变啮合刚度对揭示齿轮运行规律有意义。图4为理想与断齿故障下的斜齿轮时变啮合刚度变化。对比可知，断齿故障下齿轮副综合啮合刚度在故障接触区域中低于相应理想下齿轮副综合啮合刚度。断齿故障啮合区下的综合啮合刚度大幅度降低，但由于斜齿轮交叉啮合，其断齿故障综合啮合刚度不会为零。

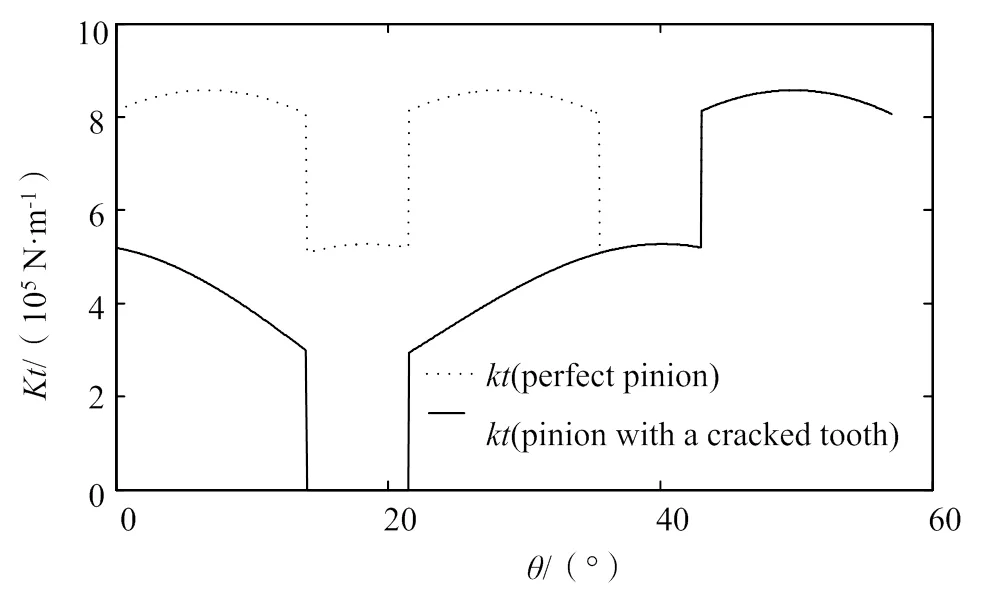
图3 断齿条件下综合啮合刚度变化

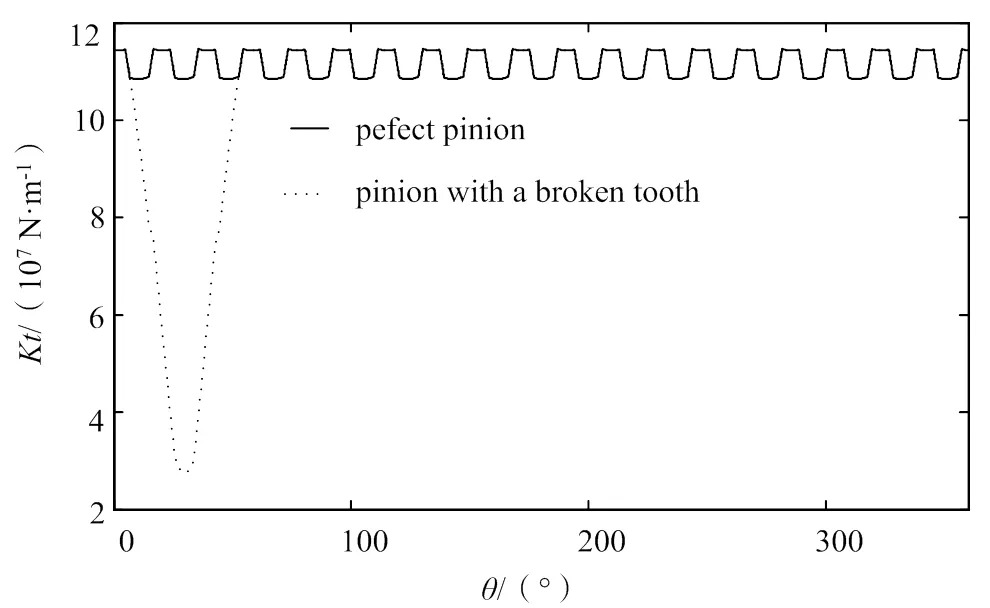
图4 断齿条件下斜齿轮综合刚度变化

3 斜齿轮扭转振动动力学模型

以单级断齿故障斜齿轮传动系统为研究对象，采用集中质量法建立了齿轮时变啮合刚度、时变啮合阻尼、静态传递误差及摩擦激励的斜齿轮副单自由度动力学模型。模型如图5所示。

由牛顿第二定律可得扭转振动的动力学方程为：

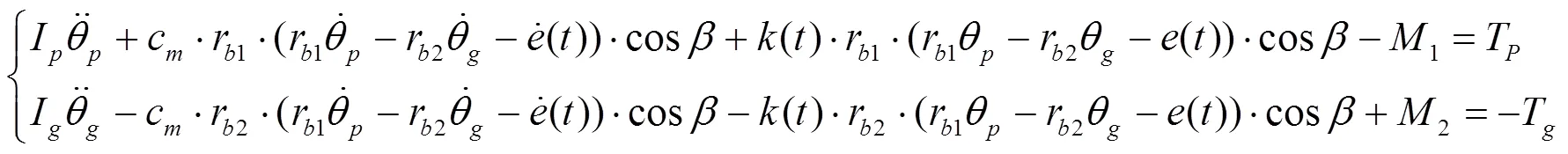
式中：Ip、Ig分别为小齿轮和大齿轮转动惯量；Tp、Tg分别为小齿轮和大齿轮施加恒定扭矩；M1、M2分别为小齿轮和大齿轮上时变摩擦力矩；θp、θg分别为小齿轮和大齿轮转角；β为分度圆螺旋角；rb1、rb2分别为小齿轮和大齿轮基圆半径；k (t)为时变啮合刚度；cm为啮合阻尼；e(t)为轮齿综合误差。

针对本文中给出的传动系统参数及模型，运用2012版本的fortran仿真软件，采用变阶Runge-Kutta法求解得到断齿故障斜齿轮传动系统的振动响应。

4 斜齿轮扭转振动动力学特性分析

4.1 转速对斜齿轮扭转振动动力学特性的影响

图6～8给出了扭矩50000 N·m、转速分别为3785 r/min和5785 r/min时的动力学特性。

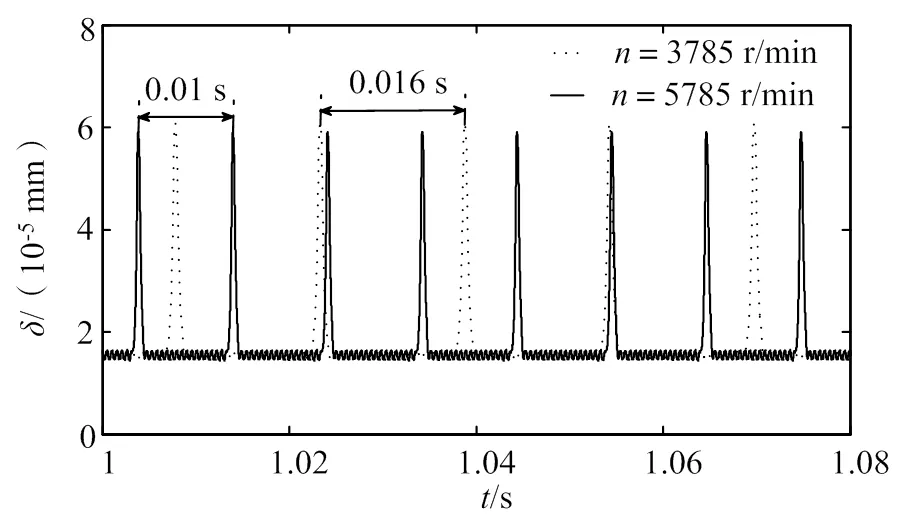
图6 不同转速条件下动态传递误差变化

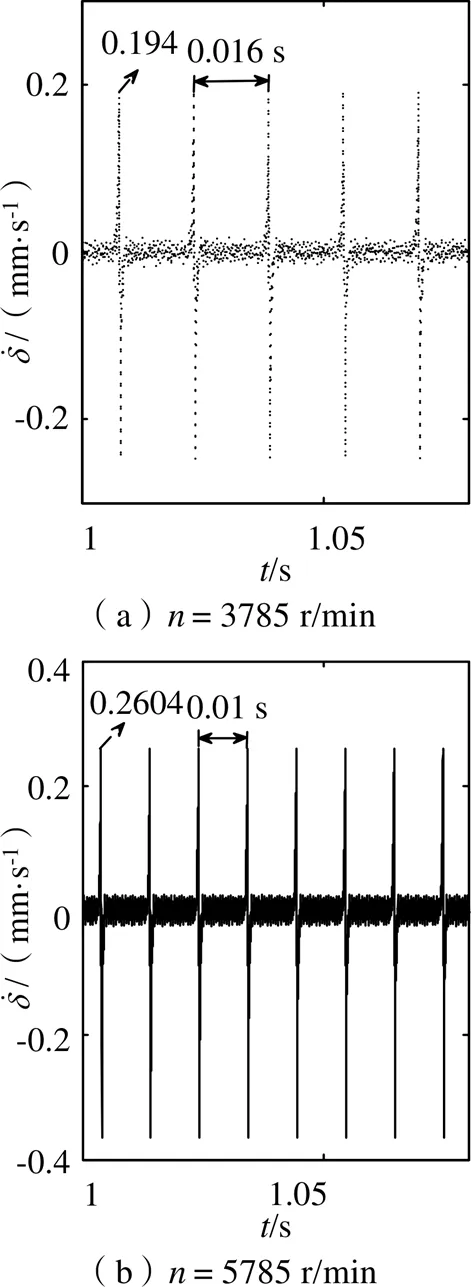
图7 不同转速条件下振动速度变化

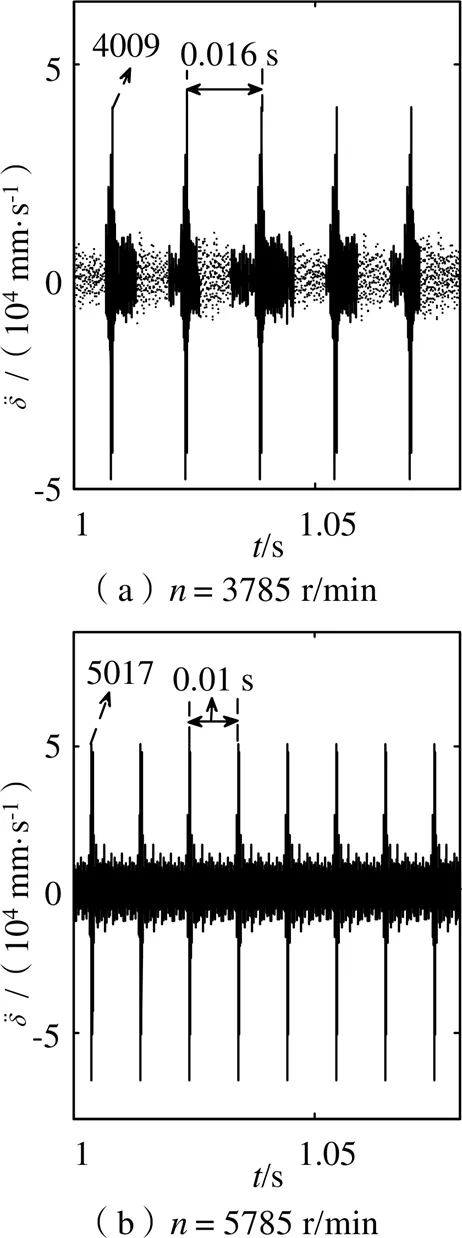
图8 不同转速条件下振动加速度变化

如图6所示，断齿故障的轮齿在不同转速下的动态传递误差存在周期性冲击响应间隔、振动响应强烈，分别为0.016 s和0.01 s，转速小的冲击间隔是转速大的冲击间隔的1.6倍。如图7所示，断齿故障的轮齿在不同转速下的振动速度存在周期性冲击响应间隔、振动响应强烈，最大分别为0.194 mm/s和0.2604 mm/s，转速较大时振动速度较平稳剧烈。如图8所示，断齿故障的轮齿在不同转速下的振动加速度存在周期性冲击响应间隔、振动响应强烈，最大分别为4009 mm/s2和5017 mm/s2，转速较大时振动加速度较平稳剧烈。

4.2 扭矩对斜齿轮扭转振动动力学特性的影响

图9～11给出了转速3785 r/min、扭矩分别为500 N·m和50000 N·m时的动力学特性。可以看出，含有断齿故障的小齿轮在不同扭矩条件下呈现明显的周期性，振动响应强烈。

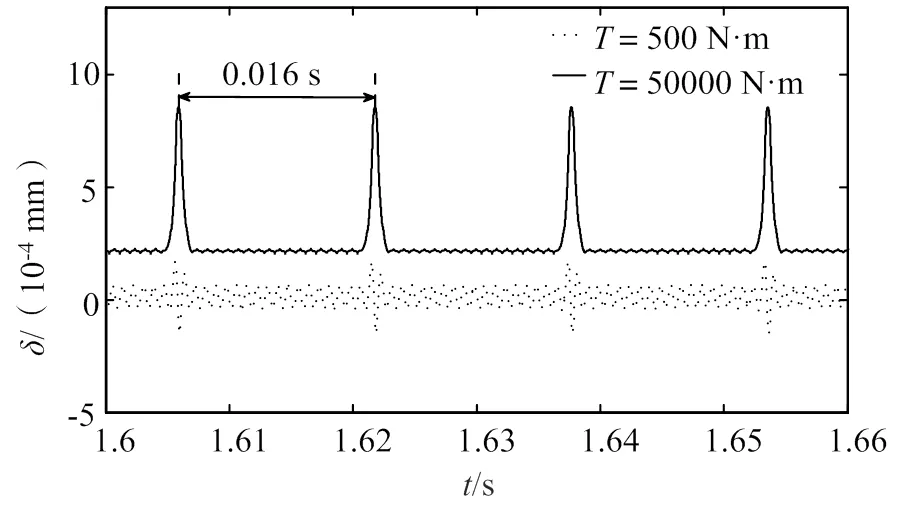
图9 不同扭矩条件下动态传递误差变化

如图9所示，扭矩为50000 N·m的动态传递误差高于扭矩为500 N·m的动态传递误差。如图10所示，振动速度分别为1.406 mm/s和2.735 mm/s，扭矩较大时振动速度响应较平稳剧烈。如图11所示，振动加速度最大分别为6716 mm/s2和56500 mm/s2，扭矩较大时振动加速度振动响应越平稳强烈。

4.3 断齿故障对斜齿轮扭转振动动力学特性的影响

转速3785 r/min时轮齿转频63 Hz、啮合频率1198 Hz。图12～14给出无故障条件下与扭矩500 N·m、转速3785 r/min时断齿故障条件下的动力学时域响应变化与相应频域变化。

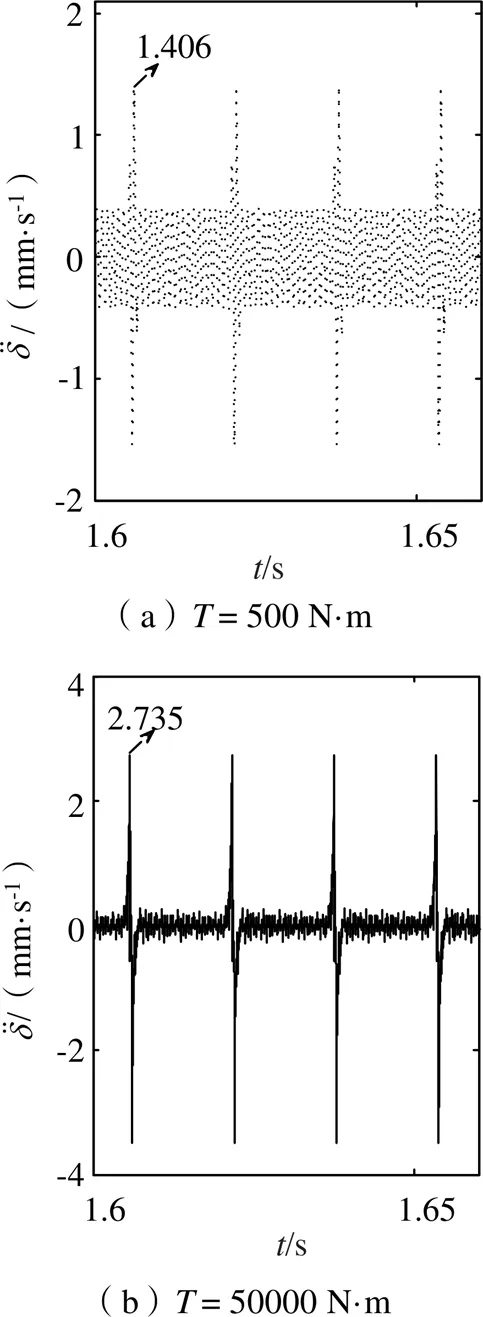
图10 不同扭矩条件下振动速度变化

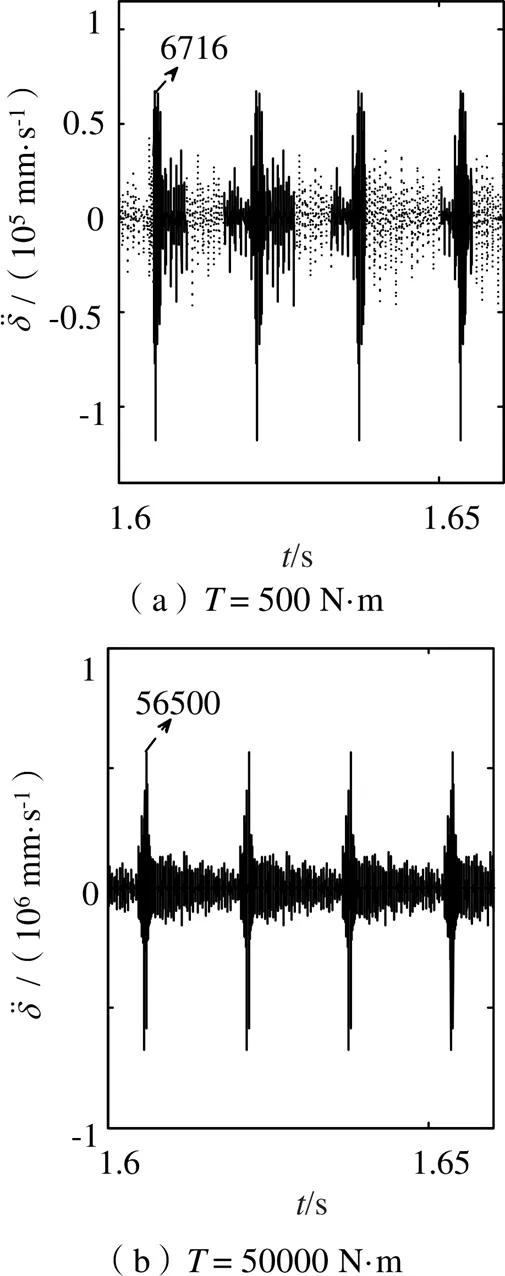
图11 不同扭矩条件下振动加速度变化

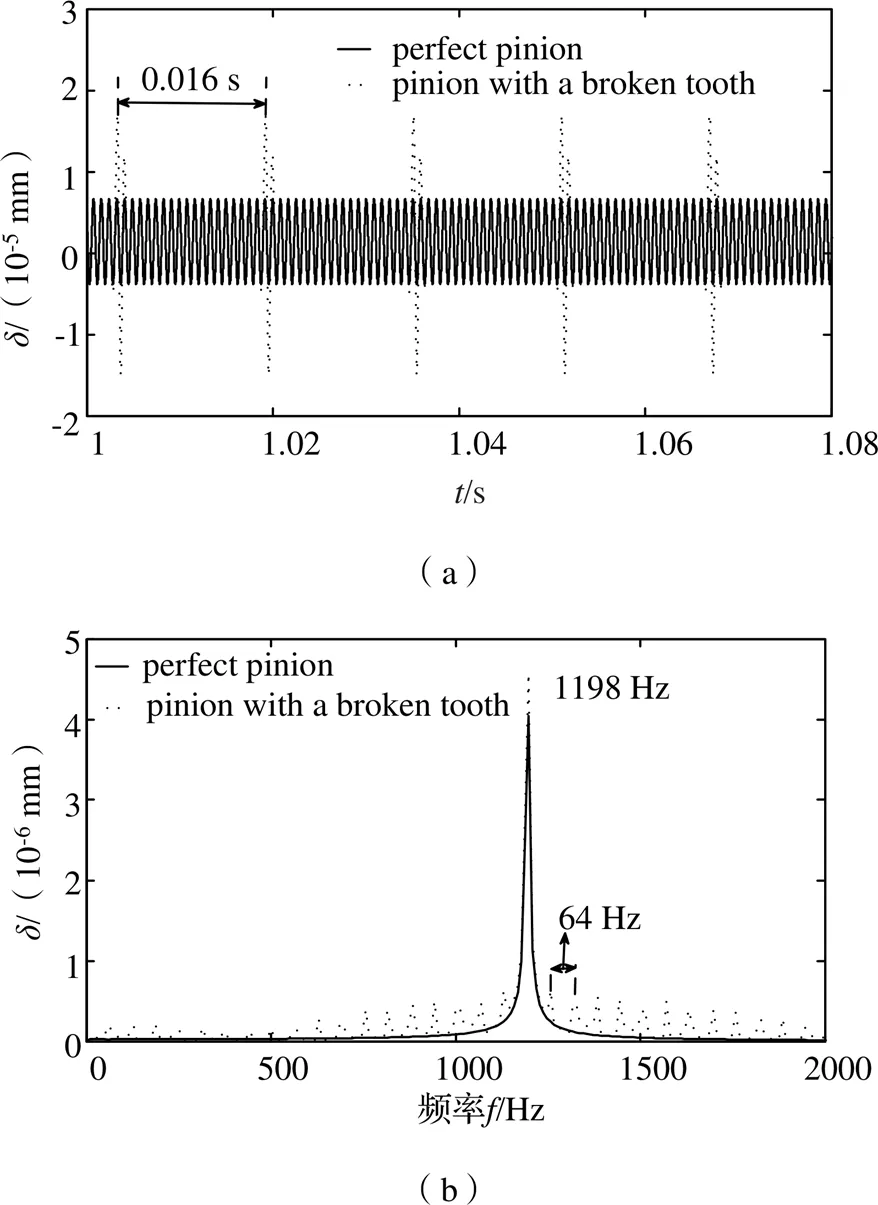
图12 动态传递误差时域振动响应变化与相应频域变化图

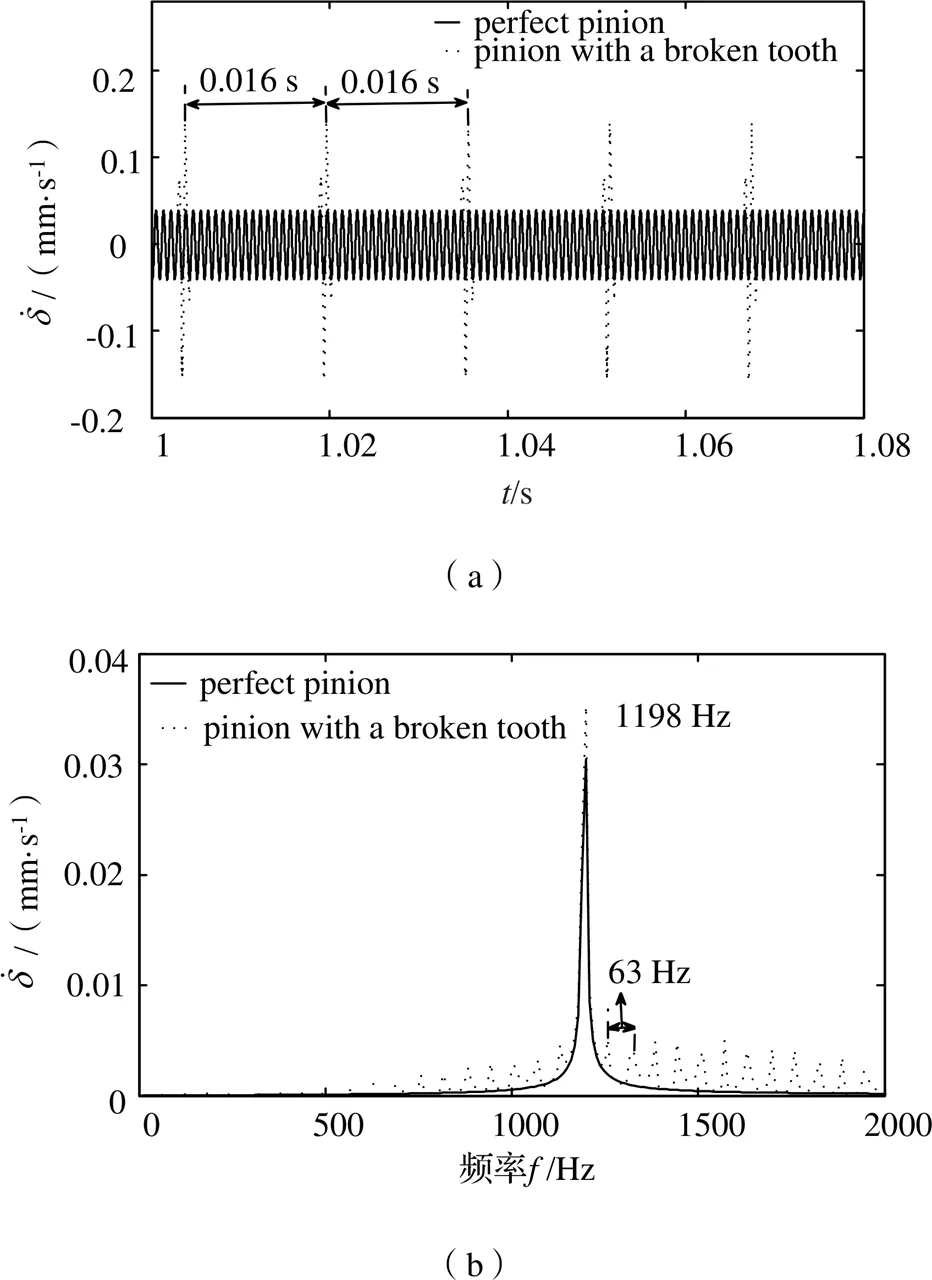
图13 振动速度时域振动响应变化与相应频域变化图

如图12（a）所示，断齿故障下的动态传递误差时域响应存在周期性冲击响应间隔，高于无故障下的时域响应。如图13（a）所示，断齿故障下的振动速度时域响应存在周期性冲击响应间隔，高于无故障下的时域响应。如图14（a）所示，断齿故障下的振动加速度时域响应存在周期性冲击响应间隔、最高6748 mm/s2，无断齿故障下的时域响应为4124 mm/s2，断齿故障下的时域响应高于无故障下的时域响应。

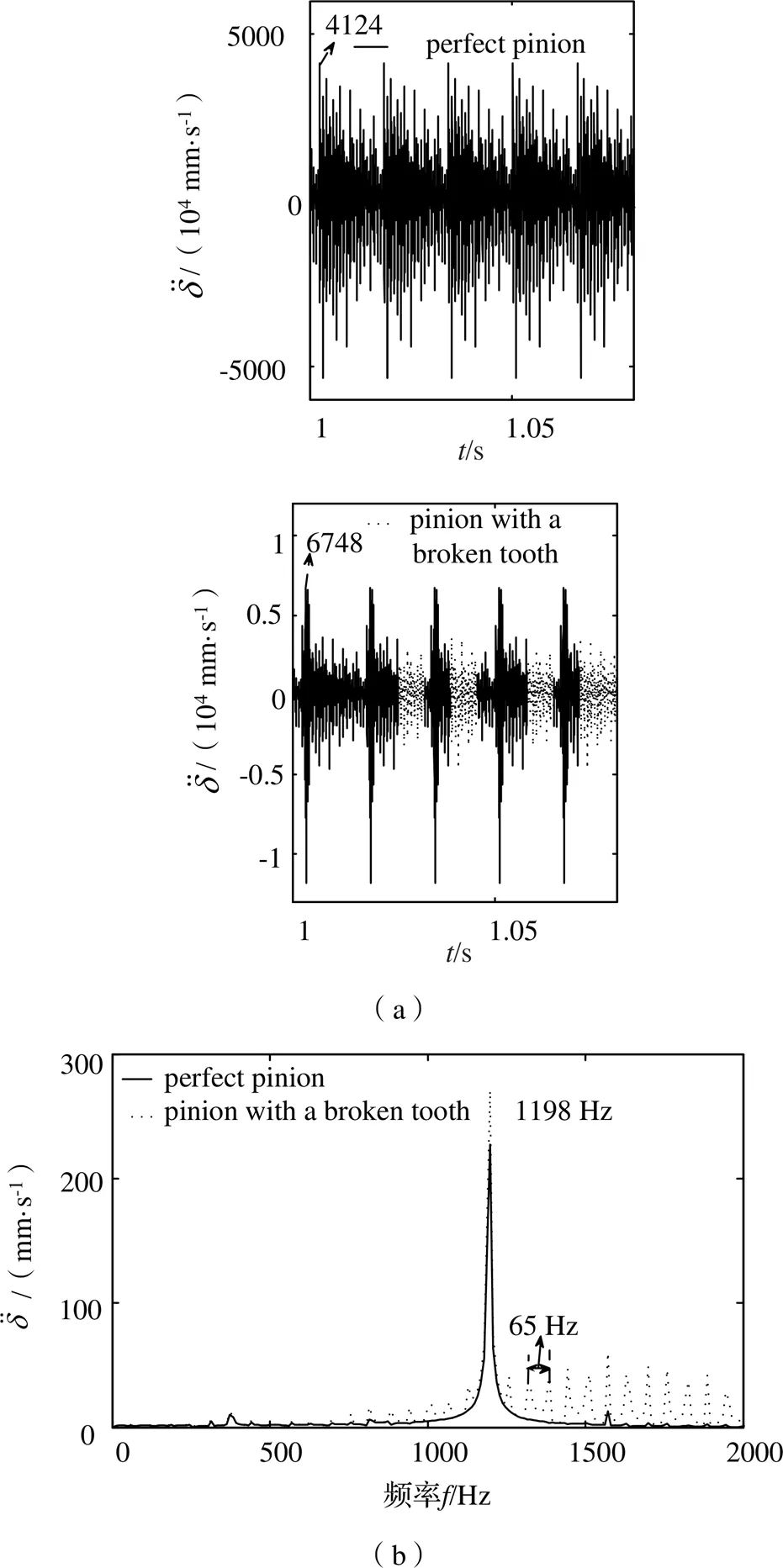
图14 振动加速度时域振动响应变化与相应频域变化图

如图12（b）、图13（b）、图14（b）所示，在无故障条件下与在扭矩500 N·m、转速3785 r/min时的断齿故障条件下的动态传递误差、振动速度、振动加速度时域对应的频域响应谱中出现以啮合频率为中心的调频边带，断齿故障下的动态传递误差、振动速度、振动加速度频域响应谱中出现明显的变频振动效应，断齿故障下轮齿的边频效应和振动幅频高于无断齿故障下的边频效应和振动幅频、动态传递误差响应谱中其中相邻两个边频效应频率间隔为64 Hz、啮合频率为1198 Hz。振动速度响应谱中其中相邻两个边频效应频率间隔为63 Hz、啮合频率为1198 Hz。振动加速度响应谱中其中相邻两个边频效应频率间隔为65 Hz、啮合频率为1198 Hz，断齿故障的存在导致边频效应的转频不一致，振动加速度响应谱中边频效应高于动态传递误差和振动速度边频效应。轮齿的转频与啮合频率相对应于断齿故障齿轮的转频与啮合频率。该变化下的动力学特性可用于分析传动系统的断齿故障的存在。

5 结论

利用建立的断齿故障下的三维模型及动力学模型，总结一对单级传动系统斜齿轮断齿故障因素的时变啮合刚度变化及传动系统动态特性规律，得出如下结论：

（1）断齿故障的存在影响了轮齿的啮合时变刚度，进而影响了系统的动力学响应。

（2）断齿故障对齿轮副啮合刚度的影响较大，出现断齿区域部分的齿轮，综合啮合刚度会有较大幅度的减小。

（3）建立了含断齿故障的传动系统动力学模型，通过动力学仿真得出，存在断齿时系统动态传递误差，振动速度和振动加速度出现了周期性的冲击响应现象，转速越大时系统的动态传递误差振动响应越快，振动速度和振动加速度越大，振动响应越平稳强烈。扭矩大的动态传递误差高于扭矩小的动态传递误差，振动速度和振动加速度越大，振动响应越平稳强烈。系统的相邻两个冲击间隔时间为断齿故障齿轮传动周期，频域响应中出现了以啮合频率及其倍频为中心的调频边带，边频间隔为断齿故障啮合齿轮转频。

[1]林腾蛟，郭松龄，赵子瑞，等. 裂纹故障对斜齿轮时变啮合刚度及振动响应的影响分析[J]. 振动与冲击，2019，38（16）：29-36，63.

[2]马锐，陈予恕. 含裂纹故障齿轮系统的非线性动力学研究[J]. 机械工程学报，2011，47（21）：84-90.

[3]朱丽莎，王奇斌，栾晓刚，等. 基于切片耦合理论的斜齿轮时变啮合刚度分析[J]. 振动与冲击，2022，41（10）：66-71，80.

[4]万志国，訾艳阳，曹宏瑞，等. 时变啮合刚度算法修正与齿根裂纹动力学建模[J]. 机械工程学报，2013，49（11）：153-160.

[5]SAXENA A，CHOUKSEY M，PAＲEY A. Effect of mesh stiffness of healthy and cracked gear tooth on modal and frequency response characteristics of geared rotor system[J]. Mechanism and Machine Theory，2017（107）：261-273.

[6]Feng M，Ma H，Li Z，et al. An improved analytical method for calculating time-varying mesh stiffness of helical gears[J]. Meccanica Journal of the Italian Association of Theoretical &Applied Mechanics，2018（53）：1131-1145.

[7]Wang Q，Zhao B，Yang F，et al. An improved time-varying mesh stiffness model for helical gear pairs considering axial mesh force component[J]. Mechanical Systems and Signal Processing，2018（106）：413-429.

[8]肖正明，郇立荣，曹金鑫. 裂纹故障对行星齿轮传动系统动力学特性的影响[J]. 振动与冲击，2020，39（2）：188-194.

[9]王彦刚，郑海起，杨通强，等. 故障参数下齿轮系统非线性动力学行为[J]. 振动，测试与诊断，2011，31（5）：570-573，662.

[10]强仕杰，何泽银，孙世政. 过载断齿故障下船用斜齿轮副啮合刚度计算[J]. 机械强度，2021，43（6）：1492-1497.

[11]严作堂，陈宏. 基于振动信号诊断齿轮断齿故障新方法[J]. 机械传动，2012，36（9）：93-95.

[12]陈宝庆，叶福民. 两级行星齿轮断齿故障的动态特性分析[J]. 机械制造与自动化，2019，48（6）：51-54.

[13]TIAN X. Dynamic simulation for system response of gearbox including localized gear faults[D]. Canada：University of Alberta，2004.

Research on Dynamic Performance of Helical Gear Pair Based on Tooth Breakage

YAN Chun’ai1，LIU Mingyong2，DENG Enxi2，HAN Xinguang2

(1.College of Intelligent Manufacturing, Wuchang Institute of Technology, Wuhan 430065, China; 2.Hubei Province Agricultural Equipment Intelligent Engineering Technology Center, Hubei University of Technology, Wuhan 430068, China )

In order to explore the dynamic characteristics of gear transmission system caused by tooth breakage, considering the factors of Hertz, bending, shearing and axial compression, the time-varying meshing stiffness of the gear is studied through the potential energy method combined with the slicing method. Considering the time-varying meshing stiffness, time-varying meshing damping, static transmission error, friction excitation and other factors, on the basis of the helical gear dynamic model, the Runge-Kutta method is used to study the influence of the fault parameters on the system dynamic characteristics. The results show that the comprehensive and effective meshing stiffness of the gear with tooth breakage is greatly reduced, the periodic shock occurs in the dynamic transmission error, vibration velocity and vibration acceleration in the system, and the side frequency signal centered on the meshing frequency appears in the frequency domain response. The research results can effectively realize the transmission failure identification of the gears with tooth breakage.

tooth breakage；meshing stiffness；dynamic model；periodicity

TH132.41

A

10.3969/j.issn.1006-0316.2023.07.009

1006-0316 (2023) 07-0058-08

2022-10-18

武昌工学院校级科学研究项目（2022KY03）；现代制造质量工程湖北省重点实验室开放课题（KFJJ-2022013）

闫春爱（1985－），女，河北唐山人，硕士，讲师，主要研究方向为齿轮设计，E-mail：664874648@qq.com。*通讯作者：刘明勇（1985－），男，江西九江人，副教授，博士，主要研究方向为机械动力学，E-mail：lmy8508@qq.com。