基于HyperWorks的反力架优化设计

廖嵘，杨帆，许为，张振麒

基于HyperWorks的反力架优化设计

廖嵘，杨帆，许为，张振麒

（柳州泰姆预应力机械有限公司，广西 柳州 545000）

运用HyperWorks的尺寸优化功能对挤压机受力部件的反力架进行优化分析。经过静力分析、第一次优化、重新调整优化参数和第二次优化，最终满足目标函数和约束函数要求，得出了最优的设计方案，最终优化结果较初始方案材料减少38.0%，既满足了强度与刚度的设计要求，又降低了成本。其间运用Shell壳单元和Beam梁单元替代实体单元简化模型，并使用其1/2模型进行对称分析，从而大大减少了网格数量，提高了运算速度和效率；应用第二类响应功能创建约束函数，较好地解决了直接调用第一类响应无法处理的问题。

反力架；有限元；对称分析；第二类响应

随着公路梁用工作锚板孔挤压工艺的成熟及广泛应用，为了适应可挤压工作锚板2～22孔的需要，设计开发一套2工位且单工位最大可承受4.9×106N力的挤压机，因此在重载荷作用下整个反力架结构的强度和变形问题显得至关重要。柴振岭等[1]运用有限元数值分析与理论分析相结合的方法成功研制了拉压双作用梁式反力架，出于安全性和稳定性的考虑对反力架的强度和刚度进行了校验，未对反力架进行优化分析；王凯等[2]提出了在有限元分析的基础上，应用粒子群优化算法（Particle swarm optimization，PSO）求解反力架的优化问题，其实质是联合了有限元分析软件ABAQUS和多学科优化设计软件ISIGHT开展反力架的结构优化设计，通过优化分析实现了反力架轻量化和降低成本的目标，但其过程较为繁琐。

HyperWorks使用先进的优化算法和优化引擎让用户结合拓扑、形貌、尺寸和形状优化方法创建更好的设计方案[3]，其中尺寸优化被广泛应用。张积洪等[4]对车架结构进行拓扑、形貌优化和尺寸优化；张时锋等[5]运用尺寸优化对挡板门结构进行轻量化设计；徐晶等[6]运用尺寸优化对液压机机身进行结构优化。结合挤压机的反力架实际情况，先用HyperWorks对反力架进行静态力学分析，有了一个初始的分析结果，根据结果再设定设计变量、目标函数和约束函数，最后进行尺寸优化设计。

在建立约束函数和目标函数时，可直接调用内部的第一类响应计算结果，如位移、应力、作用力、接触应力、频率、柔度、体积、质量等，这些响应都可以直接调用并可转化为约束函数或目标函数。当遇到第一类响应解决不了的问题时就可以应用第二类响应[4]，即调用已有第一类响应采用内部自带常用公式进行算术运算，如SUM求和、AVG平均值、SSQ平方和、MAX最大值、MIN最小值、SUMABS绝对值求和等，也可以进行自定义函数。在对反力架的分析中将会用到以自定义函数建立第二类响应并创建约束函数进行优化分析。

响应对设计变量变化的灵敏度数值直观反映设计变量对性能的影响程度和趋势，因此可以用于快速筛选出重要的变量，并对其值进行尝试性地和有方向性地调整，经过不断的迭代运算，使其结果逐渐满足约束函数和目标函数，这样可以较快速度自动的计算出最优方案，以更少的材料成本满足强度与刚度的设计要求。

1 反力架模型建立

挤压机反力架主要由上箱梁、下箱梁、立柱、螺母压板、压垫板等组成：上、下箱梁采用钢板拼焊而成，外形尺寸1750 mm×620 mm×400 mm；连接上、下箱梁的立柱采用36根32 mm精轧螺纹钢，是具有高强度、高尺寸精度的螺纹钢筋[7]，该钢筋在任意截面处都可拧上带有内螺纹的连接螺母进行连接，上、下箱梁螺纹钢连接两端的长度为1700 mm；螺母压板和压垫板分别与上、下箱焊接成一体。反力架的三维数模如图1所示。

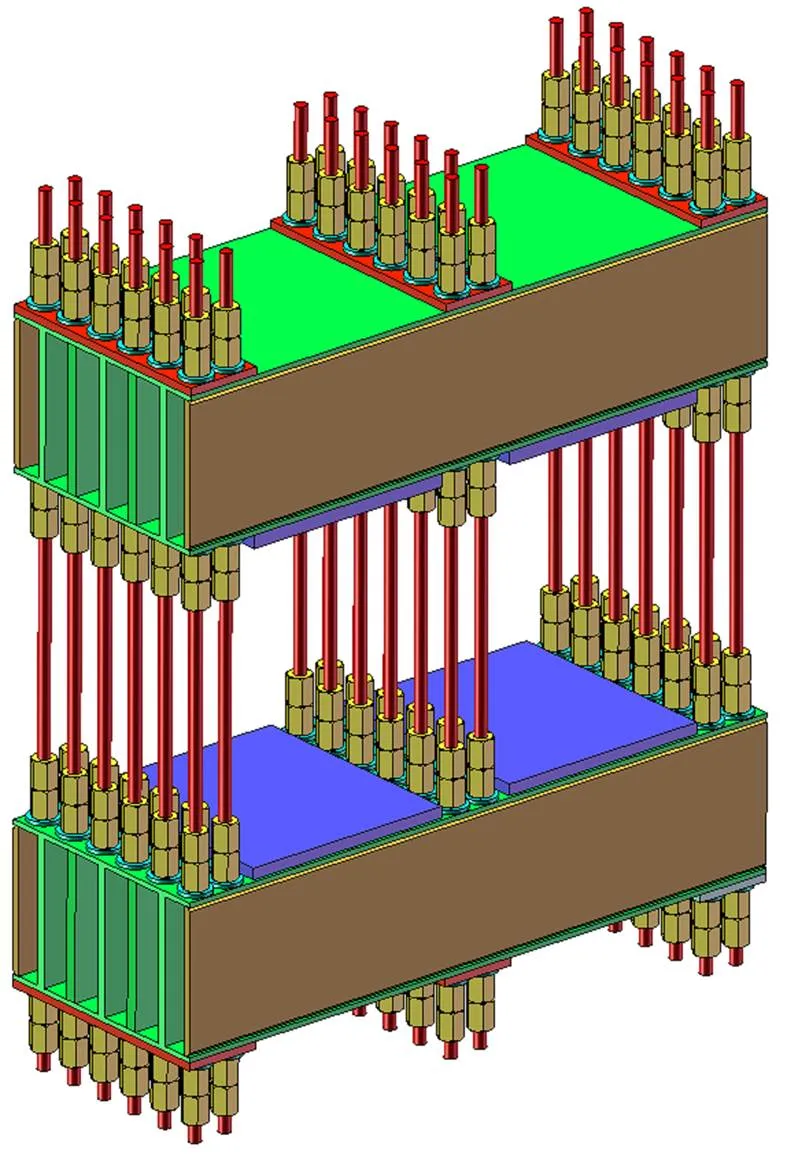
图1 反力架三维数模

1.1 划分网格

上、下箱梁都是薄板件拼焊而成，因此采用Shell壳单元[8]替换薄板件实体单元，螺纹钢采用Beam梁单元[9]，截面半径设置为16 mm。实体单元网格数量太大，会造成分析计算耗时过长，甚至会因为电脑主机性能较差而无法计算出结果。反力架模型呈对称分布，为了减少计算量，取1/2模型进行对称分析[10]。要使用对称分析必须满足3个条件，即几何形状、边界条件和载荷都具有对称性。彭春雷等[11]通过对典型的筋整体壁板进行优化设计的实例说明了对称分析的可行性，可大大节省分析时间，提高分析效率。

为便于后续优化的进行，将需优化的各板件分别命名，如图2所示，厚度根据经验都设置为40 mm，工作锚板的标准厚度为80 mm，网格尺寸设定为10 mm，得到单元数量共89153个、节点数量共86294个。

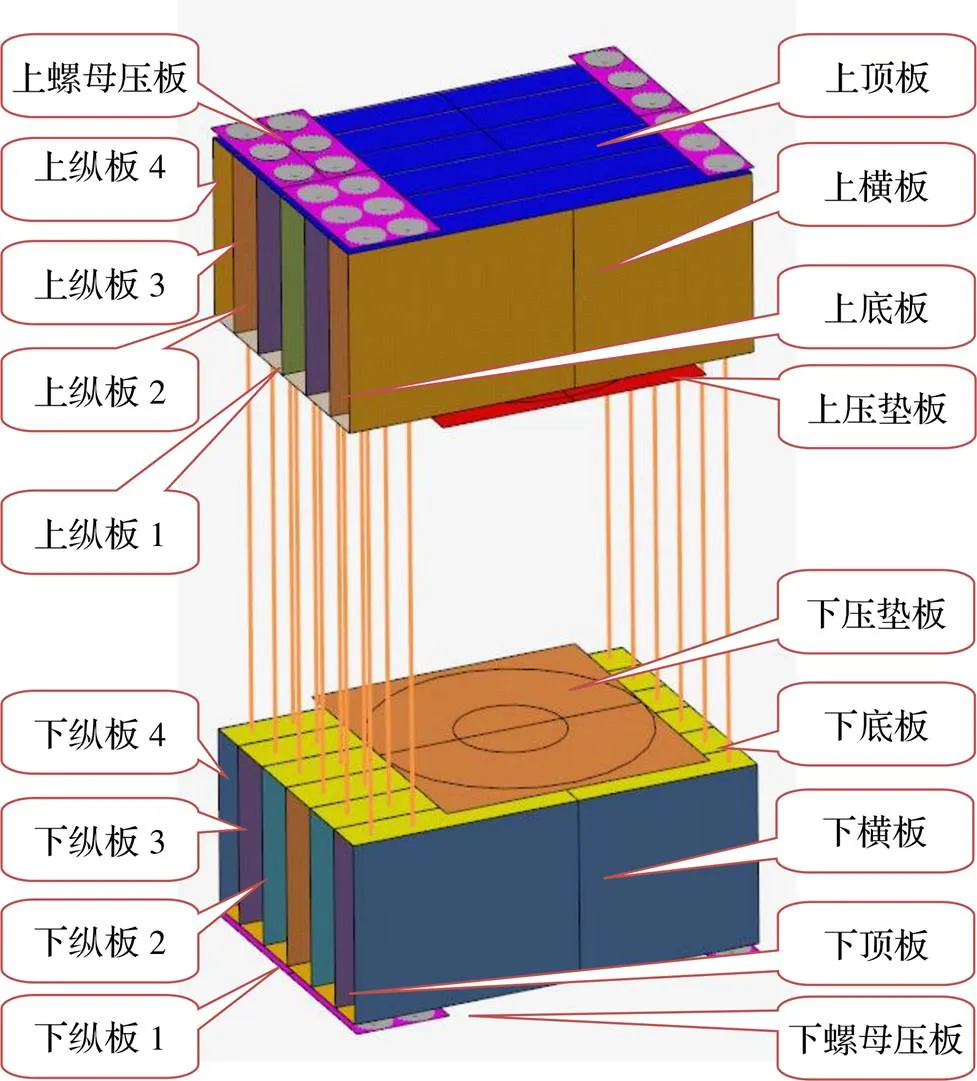
图2 各板分布图

1.2 材料属性

各部件材料属性如表1所示。

表1 材料属性

1.3 边界条件设置

1.3.1 约束边界

（1）对称约束设置：在对称面上建立一个局部坐标系，将模型所有节点归属这个坐标系，约束局部坐标系面上所有节点在方向的自由度，如图3所示；

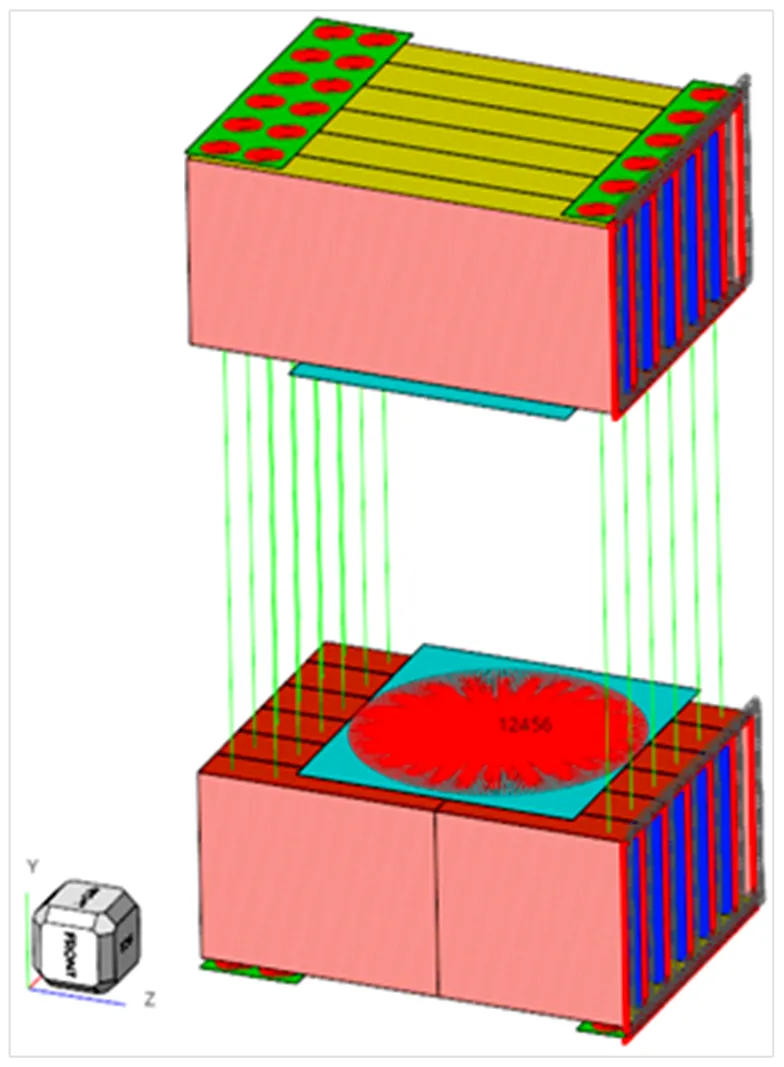
图3 对称面上的局部坐标系图

（2）下压垫板上环面（570 mm×210 mm）的所有节点与中心点耦合以刚性单元RBE2连接，约束中心节点除轴方向外其余五个方向的自由度，如图4所示；

图4 下压垫板边界约束图

（3）上螺母压板与上顶板、下螺母压板与下顶板、上压垫板与上底板、下压垫板与下底板、工作锚板与上顶板分别采用Tie绑定连接；

（4）螺纹钢Beam梁单元两端的节点分别与上、下螺母压板螺母垫圈面上的节点用刚性单元RBE3进行耦合连接代替螺母紧固[12]，如图5所示。

1.3.2载荷施加

22孔工作锚板直径226 mm，采用刚性单元RBE3将工作锚板面上所有节点与中心点耦合连接，选择最大受力工况，在耦合中心节点处轴方向施加4.9×106N的力，如图6所示。

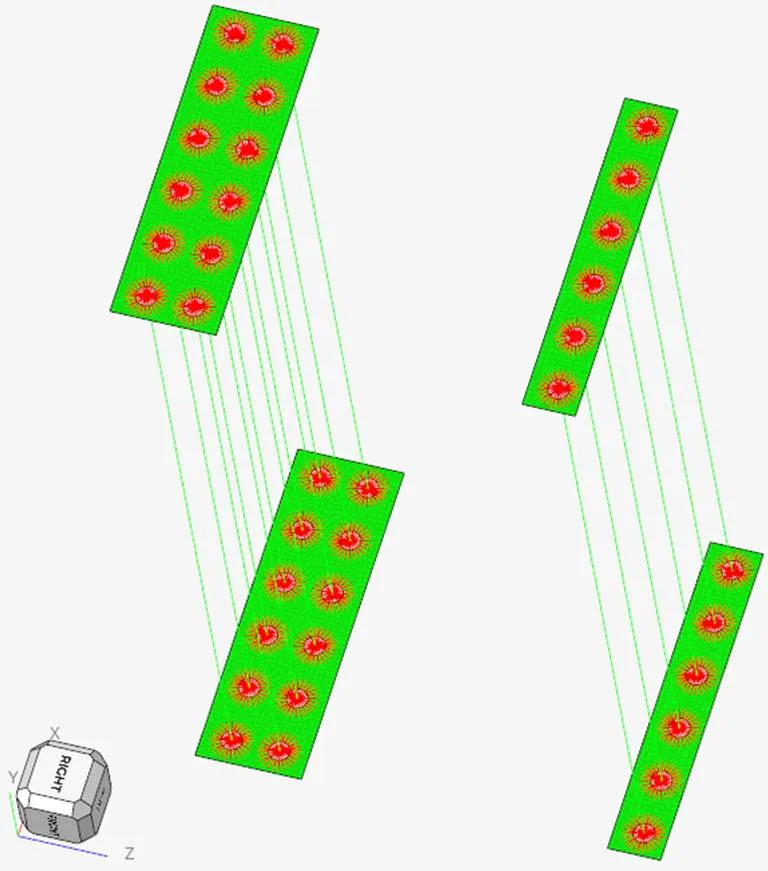
图5 RBE3单元耦合图

HyperWorks中RBE2和RBE3都是刚性杆单元，RBE2是被耦合的所有从节点与一个主节点位移始终保持一致，RBE3则是被耦合的各个主节点都可独立位移且与单个从节点构成连接关系[13]，载荷施加在从节点上，以加权方式分布在各主节点之上。

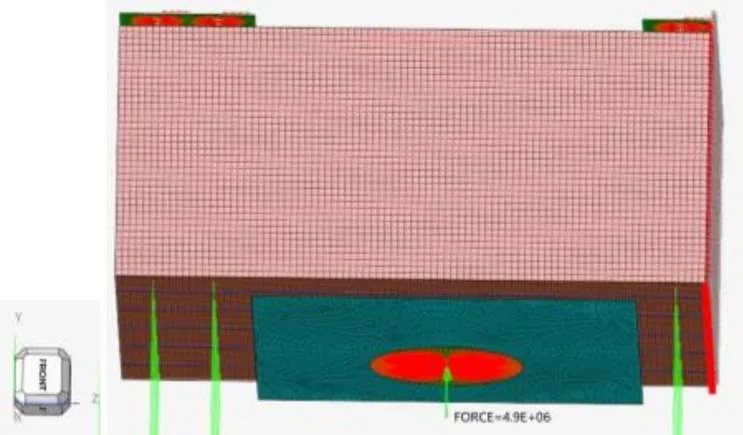
图6 载荷施加

2 初始分析

通过对反力架进行常规的线性静态分析，获得了初始的静力分析结果如图7～9所示：轴方向最大位移3.241 mm，各板最大Mises应力149.5 MPa，螺纹钢最大应力376.2 MPa。

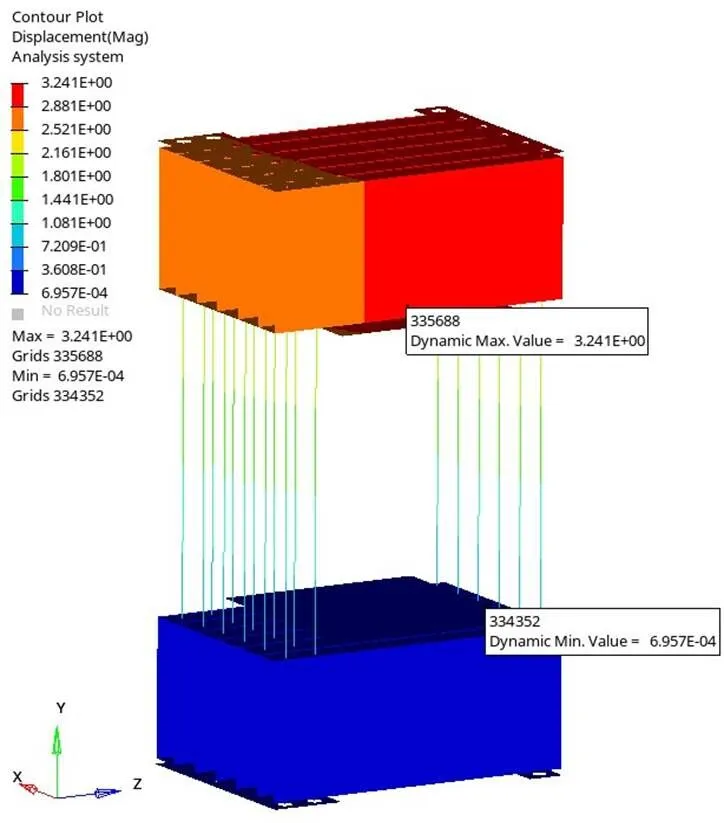
图7 位移云图（1/2模型）

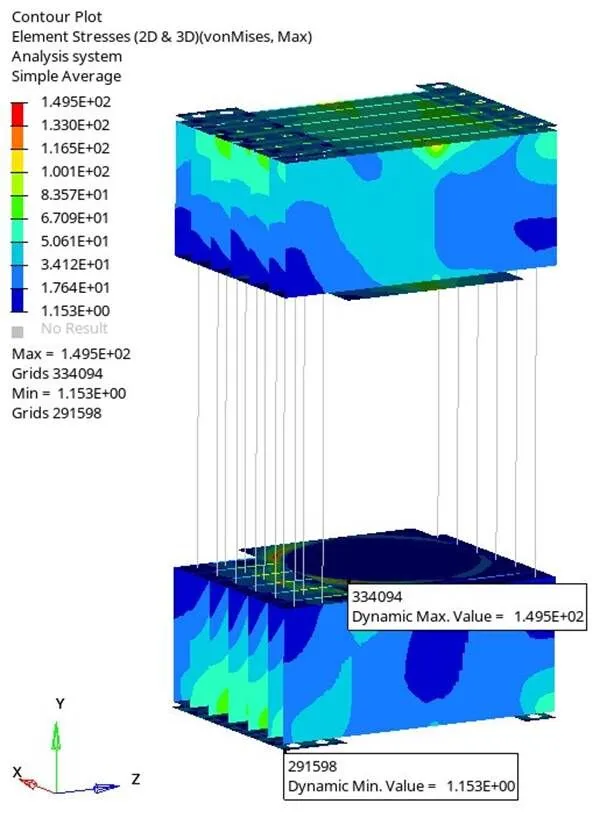
图8 各板应力云图

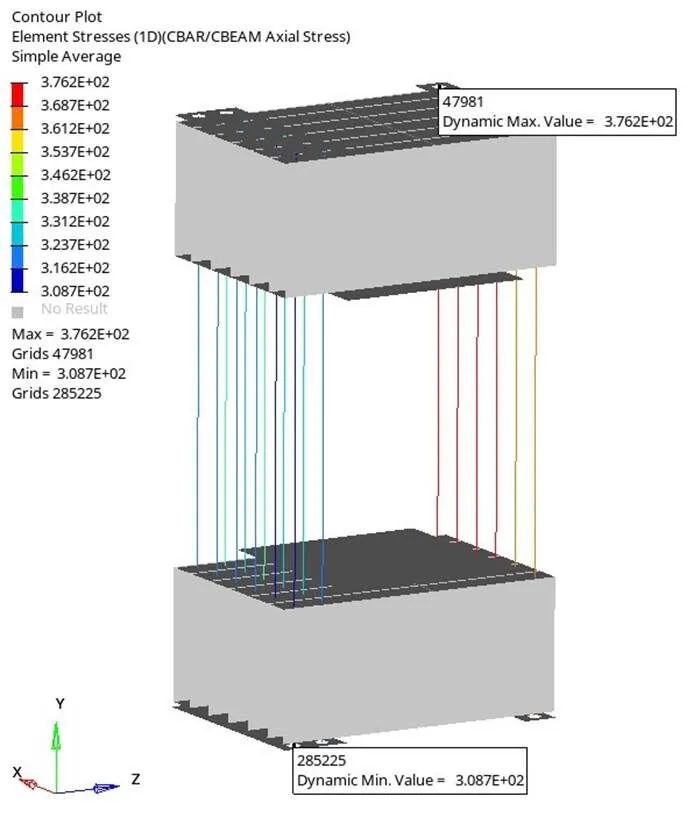
图9 螺纹钢应力云图

从图7可知：轴变形量较大，整个上箱梁整体向上位移较大的原因是螺纹钢横截面总面积较小的缘故，根据胡克定律有：

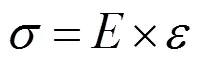
式中：为截面应力；为弹性模量；为应变。

又有：

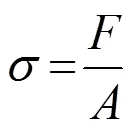
式中：为螺纹钢受到的拉力；为螺纹钢的有效面积。

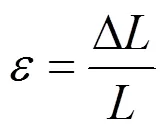
式中：Δ为螺纹钢的伸长量；为螺纹钢的两端距离。

将式（2）、式（3）代入式（1）后变换得出螺纹钢伸长量为：

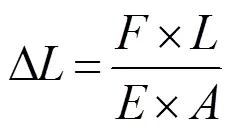
从图7（a）还可知，中间变形比两端要大，这说明在工作时上箱梁已倾斜。22孔工作锚板孔1和2之间的最大距离为132 mm（图10），调出工作锚板上1和2两点沿轴方向投影在上压垫板两点1和2的轴方向位移，节点ID号分别为284039和283965的轴方向位移差为0.063 mm（图11）。

按照JB/T 7473－2010[14]对小于1000 mm上下工作台Ⅱ级精度等级的平行度要求：

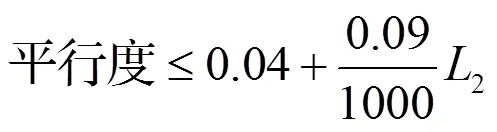
式中：L2为测量长度。

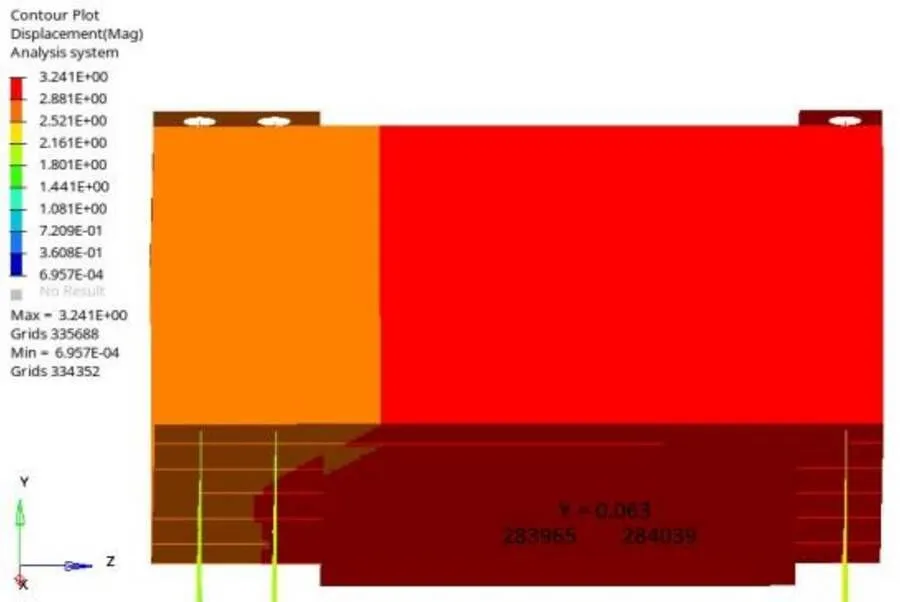
图11 两节点高度差云图

将上压垫板长度570 mm代入式（5）得到平行度为0.091 mm，再转换到长度132 mm的平行度为0.021 mm。初始分析中1和2高度差0.063 mm的结果已超出此标准要求。后续将以0.021 mm作为约束条件进行优化。

3 第一次优化

3.1 优化参数设置

3.1.1 建立设计变量

共建立18个板厚变量，优化范围设定为1～80 mm，并设置一个离散变量，输入了常用的板料厚度规格，优化过程中只从离散变量厚度中选取。

3.1.2 建立约束函数

（1）调用1和2两个节点的轴方向的位移响应，创建第二类响应，建立一个函数方程式为(1,2)＝1－2，创建约束函数为(1,2)≤0.021 mm。

（2）根据不同的材料安全系数设定最大应力值，如表2所示。

表2 各材料的最大应力设定值

（3）根据设定的拉应力创建2个应力约束函数。在建立应力响应时，采用壳单元，因为壳单元有两面，当壳单元受力弯曲时，一面为拉应力、一面为压应力、中面应力为0。Q355属塑性好的材料，受压一般不会被破坏[15]，因此优化时关注的只是拉应力的大小，应力类型选择为1。

3.1.3 建立目标函数

目标函数为体积最小化。

3.2 第一次优化后的结果

第一次优化经过30次迭代收敛，体积为4.67E+08 mm3，如图12所示，分析完成显示为不可行设计，至少违反了一个约束。

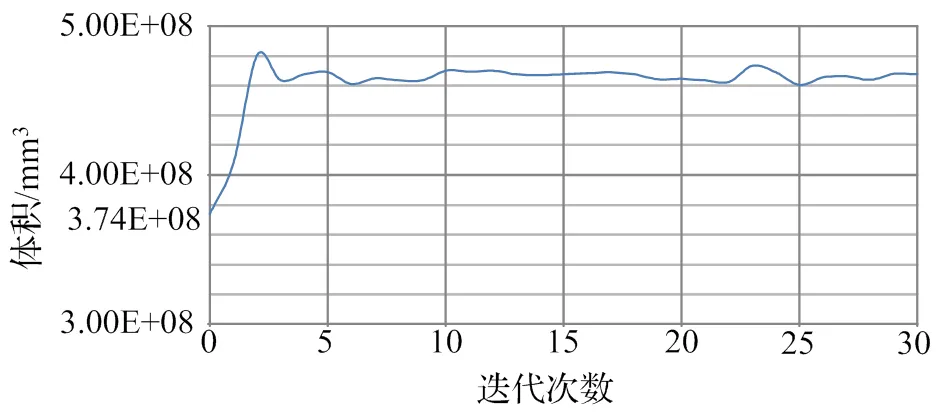
图12 第一次优化迭代图

两节点轴方向高度差0.031 mm（图13），螺纹钢最大应力383.1 MPa（图14），这两项未满足要求。

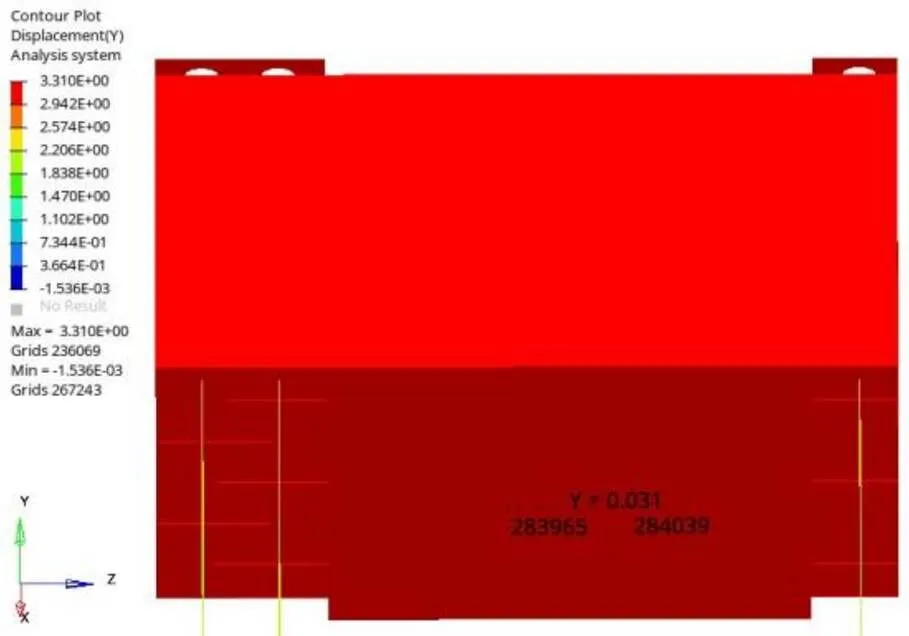
图13 两节点高度差云图

图14 螺母钢应力云图

3.3 优化结果分析

通过第一次优化结果可以看出，即使增加箱梁的体积增大梁刚度仍无法满足1、2两节点高度差的要求，究其原因：4.9×106N顶力点是在端支点和中间支点的正中位置，中间的螺纹钢支点需承受总的支反力与两端支点合力相等，而中间螺纹钢数量与两端相同都是12根，而中间比两端的变形量没有增大1倍，是由于箱体的钢度抵消了一部分力。优化过程中，其算法是通过增加板的厚度提高箱梁刚度来抵消更多的力，使得中间螺纹钢与两端的受力尽量一致，从而满足高度差要求，但板厚已优化至厚度的上限（图15），仍无法满足要求。

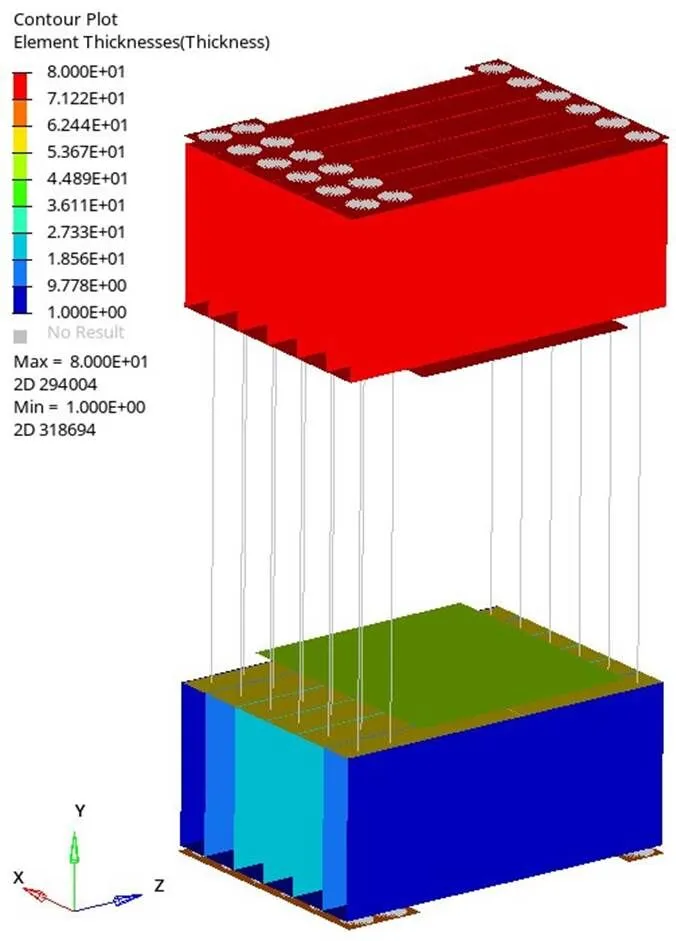
图15 第一次优化后板厚云图

4 第二次优化

要解决以上问题可从几个方面考虑：

（1）增加中间的螺纹钢的数量，但多增加一排6根螺纹钢，3排的中间1排螺纹钢在拧紧螺母会有困难，因工艺问题暂不考虑；

（2）加大中间的螺纹钢直径、减小靠两端的直径，从而减小中间和两端螺纹钢的拉伸变形量的差值；

（3）更改受力点位置，将受力点向端部偏移，会使端部的螺纹钢多承载些力，让中间和端部的螺纹钢承载力差距减小。

4.1 重新设置优化参数

（1）使用移动工具将工作锚板、上压垫板和下压垫板的壳单元往轴方向移动-20 mm，偏离中心向端部移动，上端载荷和下端的边界约束自动跟随。

（2）增加设计变量：以螺纹钢的半径作为设计变量，因空间限制，最大可以用到40 mm螺纹钢，优化范围设定为12.5～20 mm，再设置一个离散变量，优化过程中只允许选用半径规格为12.5 mm、16 mm、18 mm、20 mm的螺纹钢。螺纹钢分为9组，分组情况如图16所示；

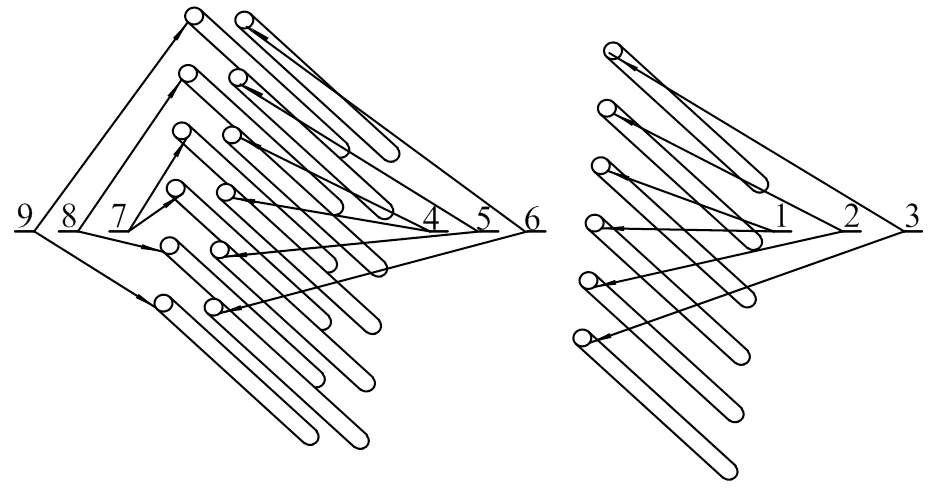
图16 螺纹钢分组图

（3）其余设计变量、约束函数和目标函数保持与第一次优化设置不变。

4.2 第二次优化后结果

第二次优化经过18次迭代收敛，体积为2.32×108mm3，如图17所示，分析完成显示为可行设计，满足所有约束。

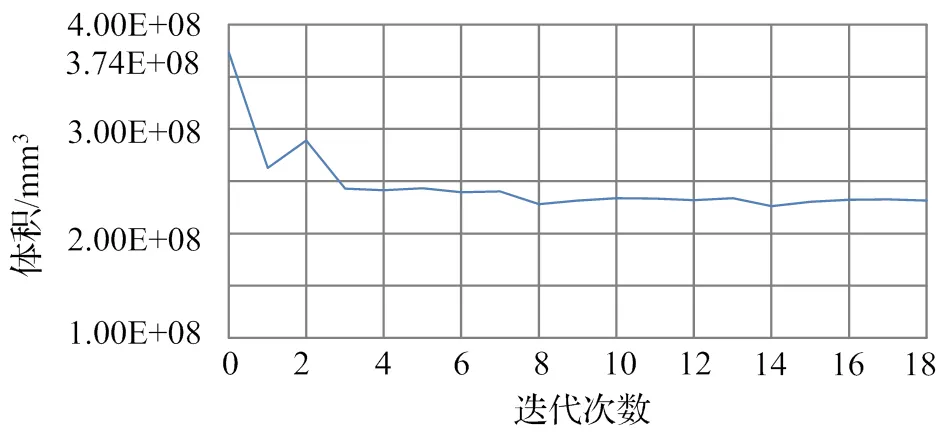
图17 第二次优化迭代图

两节点轴方向高度差0.019 mm（图18），各板最大拉应力170.8 MPa（图19），螺纹钢最大应力328.6 MPa（图20），所有约束条件满足要求。

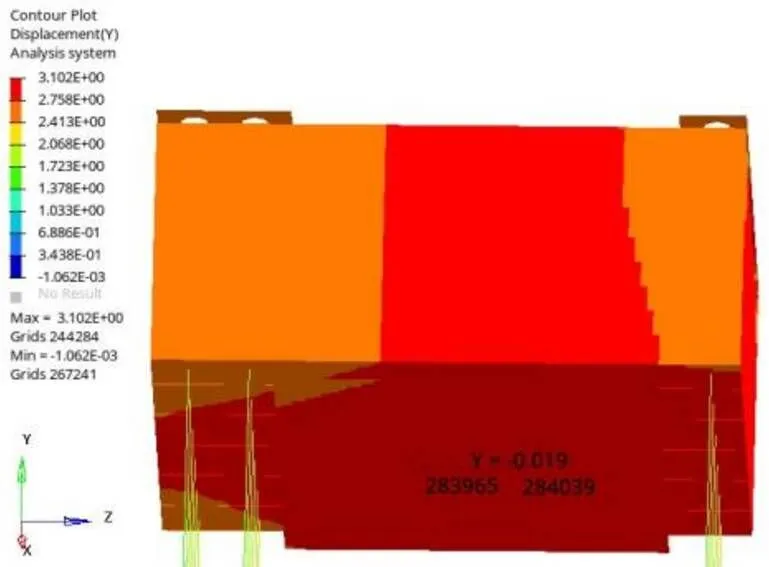
图18 两节点高度差云图

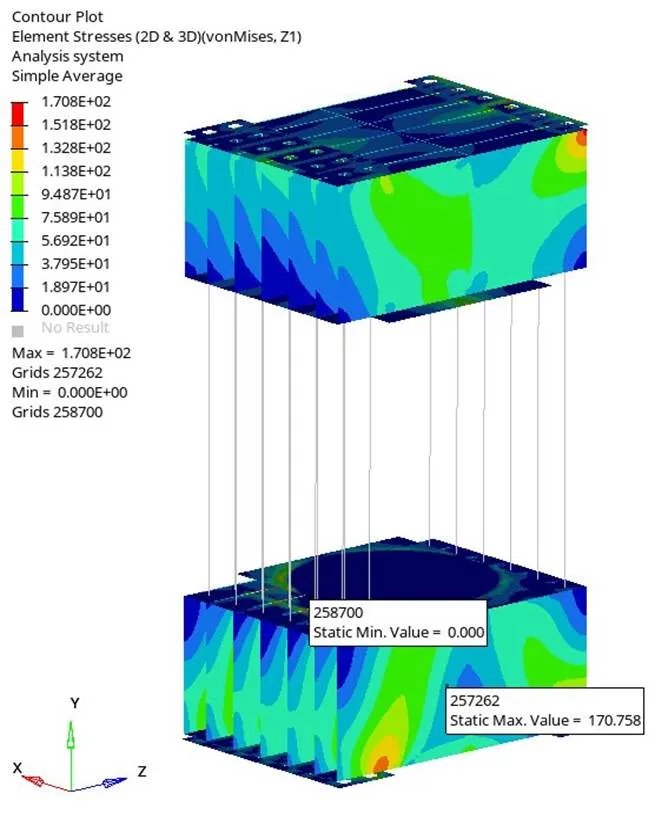
图19 各板应力云图

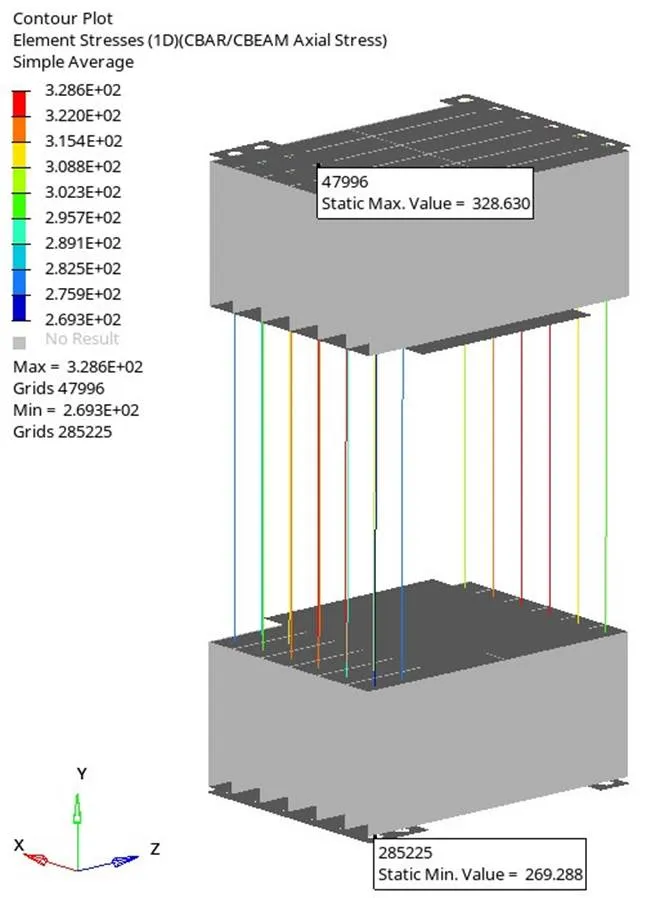
图20 螺纹钢应力云图

各板厚度优化前后对照如表3、图21所示。上、下箱梁外形尺寸是一样的，优化后上箱梁的用料比下箱梁多很多，其主要原因是上箱梁受力面积比下箱梁小，工况有所不同。同时也说明了HyperWorks在优化过程中可以做到在满足约束函数的前提下，通过增加板厚来弥补强度和刚度的不足，而对起作用较小的板通过减小板厚达到体积最小化的目的。

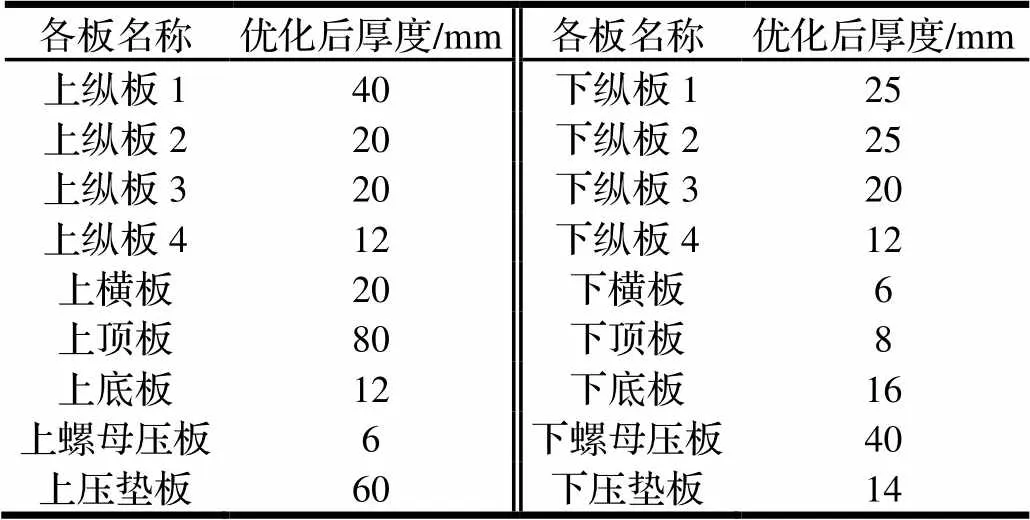
表3 优化前后各板厚度

注：优化前各板厚度均为40 mm。

螺纹钢优化前后对照如表4、图22所示。可以看出，中间的1～3组已经优化至最大，而端部的4～9组也相应地减小，优化出了最优结果。9组4个变量的排列组合有很多种，即使具有一定的理论能力，按照传统方法去尝试也会非常地费时费力，还不一定得到最优结果，从这可以看出HyperWorks的优化速度的优势是很明显的。

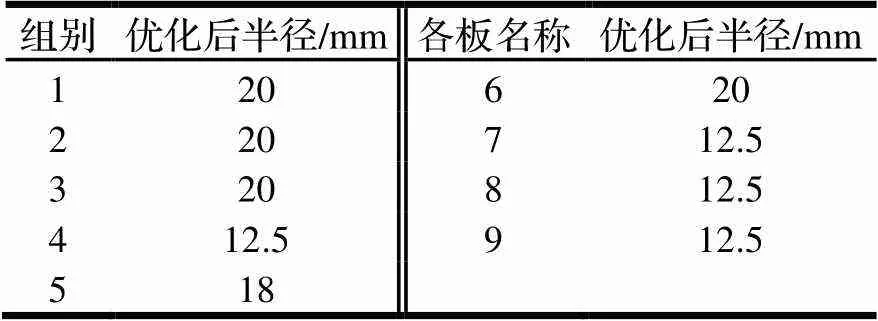
表4 优化前后螺纹钢半径

注：优化前各组螺纹钢半径均为16 mm。

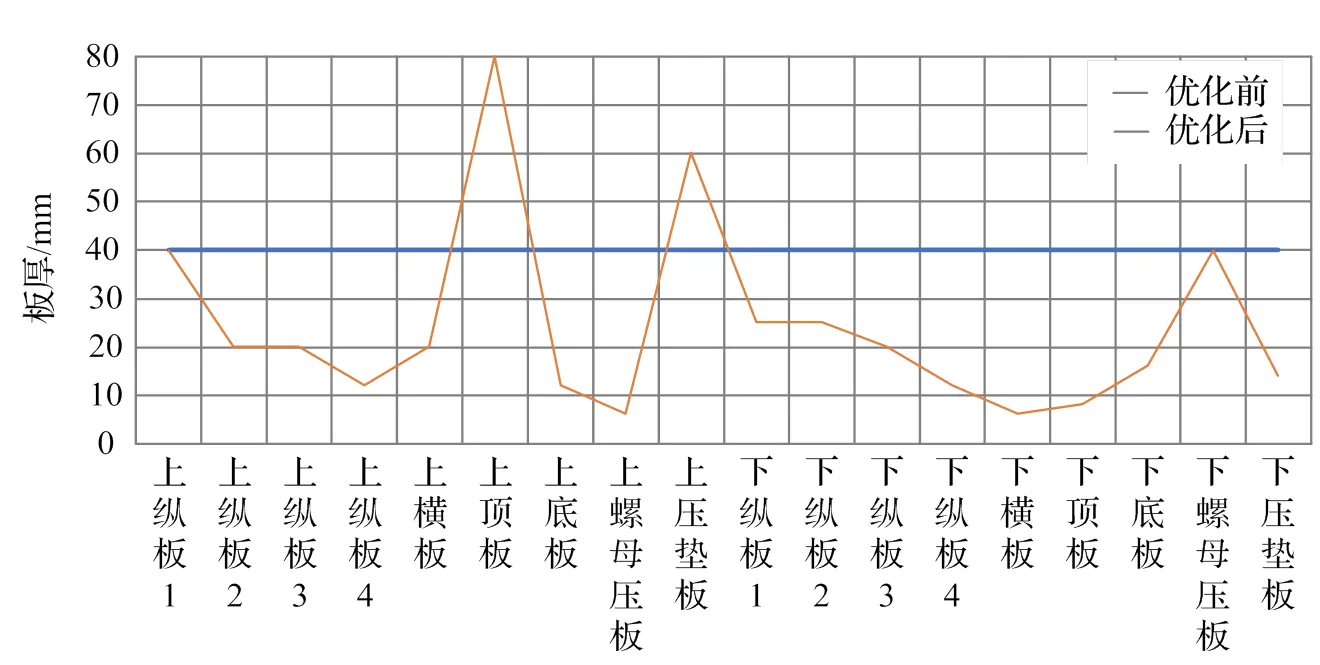
图21 各板厚度优化前后对照图

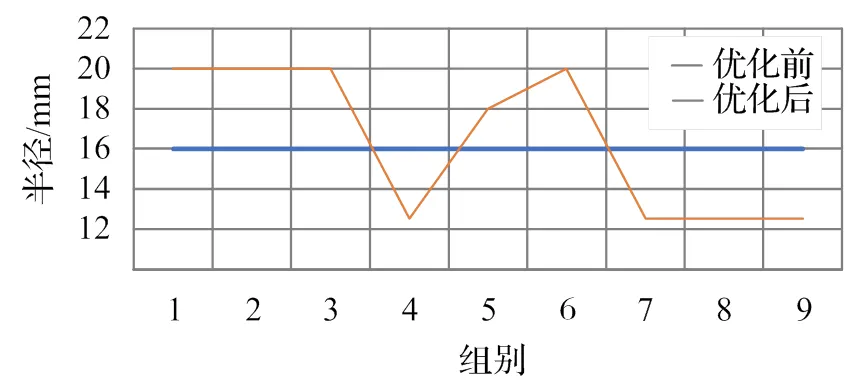
图22 螺纹钢半径优化前后对照图

5 优化效果

从表3优化前、后对比结果可知，在满足预期设计目标的前提下，优化后体积较优化前减少了38.0%。

6 小结

通过HyperWorks软件对反力架进行了优化分析，最终实现了最优的设计方案，并得到如下结论：

（1）HyperWorks尺寸优化功能强大，通过第一次优化失败和第二次优化得到最优结果的过程可以看出：只要约束函数、设计变量和目标函数设置合理，就能较快地得出最优化设计方案；

（2）对于大型结构件，尽可能使用Shell单元和Beam单元替代薄板件和杆件的实体单元，可提减少网格数量，提高计算效率，而且可以较好地利用HyperWorks的尺寸优化功能进行参数化优化设计；

（3）通过第二类响应自定义函数可较好地解决直接调用第一类响应无法满足所需要的响应的问题，对需要用第二类响应创建更为复杂的约束函数或目标函数具有一定的参考意义。

表3 优化效果表

[1]柴振岭，郭子雄，黄群贤. 拉压双作用梁式反力架的研制[J]. 实验室研究与探索，2015，34（3）：23-26，62.

[2]王凯，张良辉，孙振川，等. 基于PSO算法的反力架设计与优化[J]. 隧道建设，2019，39（2）：302-308.

[3]方献军，徐自立，熊春明. OptiStruct及HyperStudy优化与工程应用[M]. 北京：机械工业出版社，2021.

[4]张积洪，杜阳，庞玥，等. 基于HyperWorks的机场某拖车车架结构的轻量化研究[J]. 机械设计，2014，31（5）：38-41.

[5]张时锋，许小鹏，陶智森. 余热锅炉旁路挡板门壳体尺寸优化研究[J]. 机电工程，2019，36（3）：244-250.

[6]徐晶，刘基冈，张懿骅. 基于HyperMesh的液压机机身结构优化[J]. 锻压技术，2015，40（11）：48-52.

[7]中华人民共和国国家质量监督检验检疫总局中国国家标准化管理委员会. 预应力混凝土用螺纹钢筋：GB/T 20065－2016[S].

[8]郭崇志，郑彬. 基于Shell单元的压力容器结构安全与性能评价[J]. 石油机械，2009，37（1）：73-77.

[9]董永朋，王佩艳，刘洋等. 采用Beam单元模拟复合材料加筋桁条的优化分析[J]. 材料科学与工程学报，2010，28（6）：857-861，870.

[10]沈春根，孔维忠，关天龙. UG NX 11.0有限元分析基础实战 [M]. 北京：机械工业出版社，2018.

[11]彭春雷，吴雪飞，马本学. 基于ANSYS中的对称分析及其应用[J]. 机械设计与制造，2007（12）：68-69.

[12]马庆丰，汪谟清，李戈操. 基于HyperWorks的全向侧面叉车车架结构有限元分析[J]. 机电工程技术，2010，39（5）：57-60.

[13]江鹏. 飞机外蒙皮上非受力结构有限元模型设计浅析[J]. 科技创新导报，2011（12）：45-46.

[14]中华人民共和国工业和信息化部. 单双动薄板冲压液压机：JB/T 7343－2010[S].

[15]刘鸣放，刘胜新. 金属材料力学性能手册[M]. 北京：机械工业出版社，2012.

Optimal Design of Reaction Frame Based on HyperWorks

LIAO Rong，YANG Fan，XU Wei，ZHANG Zhenqi

(LiuzhouTaimu Prestressing Force MachineryCo.,Ltd., Liuzhou 545000, China )

The size optimization function of HyperWorks is used to analyze the optimization of the reaction frame of the stressed parts of the extruder. Through the static analysis, the first optimization, readjustment of optimization parameters and the second optimization, the requirements of the objective function and the constraint function are finally met, and the optimal design scheme is obtained. Meanwhile, the shell element and the beam element are used to replace the solid element to simplify the model, and its 1/2 model is used for symmetrical analysis, which greatly reduces the number of meshes and improves the operation speed and efficiency. The second type of response function of HyperWorks is used to create constraint functions. The second type of response is the algebraic expression of the first type of response, which better solves the problem that the first type of response cannot be directly called. The material needed of the final optimization result is 38.0% less than the initial scheme, which not only meets the design requirements of strength and stiffness, but also reduces the cost.

reaction frame；finite element；symmetrical analysis；the second type of response

TH123.3

A

10.3969/j.issn.1006-0316.2023.07.011

1006-0316 (2023) 007-0072-09

2022-08-08

廖嵘（1974－），男，江西龙南人，工程师，主要从事预应力设备及产品设计、研发工作，E-mail：2660255911@qq.com。