回转窑预热段温度优化及数值模拟
2023-08-26金欣玮薛长峰邱海龙张鸣鑫
金欣玮 ,薛长峰 ,邱海龙 ,张鸣鑫
(1.盐城工学院 电气工程学院,江苏 盐城 224051;2.盐城工学院 数理学院,江苏 盐城 224051)
近年来,随着水泥行业工艺设备的不断发展,人们开始广泛关注熟料煅烧流程中的高能耗和高排放问题。可以通过研究回转窑工况对窑内流场、温度场以及煤粉燃烧等因素的影响,为混凝土厂节能减排提供指导意见[1]。由于回转窑内部热传递流程的复杂性,目前的检测技术手段尚不成熟,难以精确获取回转窑内部流场和温度场的分布数据。因此,需要研究和开发更为准确的检测技术,而数值模拟能够研究回转窑内部的流场和温度场分布情况,从而更有效地控制混凝土生产流程中的能耗和排放[2-3],对于提高工程效率具有重要意义。
国内外学者针对回转窑内部流场、温度场的数值模拟进行了许多研究。Elattar等[4]建立了回转窑二维模型,研究了回转窑主要操作参数对不同燃料下火焰行为的影响;Manju等[5]将回转窑内熟料看作假流体,对窑内气流和熟料进行三维建模,建立了CFD模型,模拟了固体与固体之间的传热分布情况;Sadighi等[6]应用能量守恒和质量守恒定律,给出了一种新的数值模拟方法,通过测量过程变量和扫描壳体温度建立了水泥回转窑烧成带涂层厚度的预测模型;刘彬等[7]利用FLUENT建立了回转窑的数值模拟模型,研究了回转窑倾斜角度和不同燃烧器参数对回转窑内部流场分布的影响。
上述研究所建立的模型能够较好地模拟回转窑内物料燃烧的特性,但是未能综合考虑回转窑倾斜角度、高温气体进口速度、筒体转速等参数的影响,使得窑内整体温度场的数值模拟结果与实际情况存在较大差异。
本文建立回转窑内部湍流流动、高温气体传热和气固两相的对流换热数学模型,利用有限元方法,应用正交试验,研究气体进口速度、回转窑抬起角度和回转窑转速等对窑内热流场与温度场分布的影响。
1 回转窑预热段模型
针对回转窑内壁温度和整体温度分布不均性,设计回转窑预热段简化模型如图1所示。回转窑预热段简化模型有效长度600 mm,直径为50 mm,内壁厚度为0.4 mm,回转窑预热段模型相关物料参数如表1所示。高温气体从回转窑预热段左侧进入,经过内壁与从右侧落入的碳酸钙颗粒进行热交换,预热后的碳酸钙颗粒由左侧出口流出,达到热量传递的目的。根据实际生产经验将回转窑预热段高温气体进口温度设置为1123 K(即窑内最高温度),根据窑内最低温度的高低可以判断回转窑预热段模型传热效果的优劣。最低温度值越高,与窑内最高温度的温差越小,窑内温度分布越均匀。
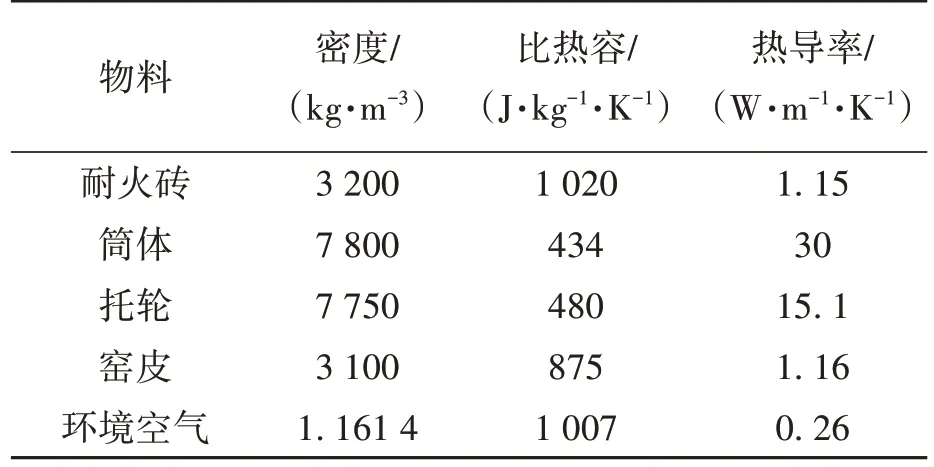
表1 回转窑预热段模型相关物料参数Table 1 Related material parameters of preheating section model of rotary kiln

图1 回转窑预热段简化模型结构示意图Fig. 1 Structure diagram of simplified model of preheating section of rotary kiln
2 回转窑传热数值模拟
2.1 条件假设
实际生产中回转窑内的运动及反应状况复杂,现对模拟过程做出如下假设:
(1) 模拟流体区域视为稳态流场,即将整个回转窑内部视为运转稳定的结构,运转时其温度、气体流速与物料进口速度等参数无关;
(2) 回转窑内部密封性完整,所有高温气体由右侧出口排放出回转窑预热段,进入燃烧准备阶段;
(3) 高温气体温度达不到产生热辐射所需的最低温度;
(4) 气体为不可压缩流体;
(5) 不考虑回转窑内的化学反应。
2.2 控制方程
2.2.1 质量守恒方程
式中:ρ为碳酸钙密度,kg/m3;t为碳酸钙物料在窑内的停留时间,s;x、y、z为三维坐标;u、v、w是坐标所对应的高温气体流速沿X、Y、Z坐标轴方向的分量。
2.2.2 能量守恒方程
式中:T为窑内温度, K;λ为窑内壁热导率,W/(m·K);ST表示黏性耗散项。
2.2.3 对流换热模型
高温气体、料层表面、未被物料覆盖的内壁之间的对流换热通过如下方程来表示:
单位长度内,窑内壁面与物料表面、高温气体与回转窑内壁、高温气体与料床表面的换热面积,由回转窑内径和抬起角度所决定,计算公式分别为:
式中:Dy为回转窑内径,m;β为回转窑抬起角度,(°)。
2.3 初始条件和边界条件
数据模拟时选用文献[8]中提供的流体边界条件和FLUENT软件中提供的热力学边界条件,选用k-ε湍流模型[9],并根据实际生产经验和表1设定相关参数。其中,换热方式为对流换热,传热系数为1.15 W/(m2·K),来流温度300 K,壁面厚度0.004 m,热源功率为0。
2.4 网格划分
为提高回转窑预热段模型计算的准确度和网格质量,利用FLUENT软件自动生成结构性网格,网格单元数为445027,网格节点数为432936。
2.5 计算方法
利用ANSYS FLUENT 2022 R1数值软件进行模拟仿真求解,采用有限元方法进行计算,其中涉及的数学模型有控制方程公式(1)~公式(8)、k-ε模型和离散项模型,选择耦合算法对模型进行求解。模拟过程中,设定高温气体进口为速度进口,高温气体出口为压力出口。在抬起角度为1°的情况下,设定回转窑运行时间为300步长,步长为1 s,并且每个步长迭代10次。
2.6 仿真结果分析
将相关参数代入FLUENT求解,可以得到回转窑预热段内部温度场分布如图2所示。由图2可知,回转窑预热段内温度从左侧高温气体进口开始沿着窑长方向逐渐降低,在右侧碳酸钙进口处温度最低。这是由于从回转窑预热段左侧进入的高温气体(1123 K)与从右侧进入的室温下的碳酸钙物料(300 K)逆流接触,高温气体将热量传递给碳酸钙物料和窑内壁,高温气体温度下降,碳酸钙物料和窑内壁温度上升,回转窑预热段内部形成了温度分布。

图2 回转窑温度分布云图Fig. 2 Nephogram of temperature distribution of rotary kiln
3 正交试验分析
3.1 正交试验设计
为进一步改善回转窑预热段内物料温度的均匀性,提高回转窑的生产效率和产品品质,综合考虑各因素的影响水平后,选取进气口高温气体的流速、回转窑的转速和回转窑的抬起角度等3个影响因素进行正交试验,以寻找最佳参数组合条件,优化仿真模拟结果。每个因素选取3个水平,高温气体流速(因素A)分别取1、2、3 m/s;回转窑转速(因素B)分别取0.2、1.6、3.5 r/min;回转窑抬起角度(因素C)分别取1°、2°、4°,正交试验因素水平如表2所示,其中,A1B1C1方案为生产厂家常用的初始方案。
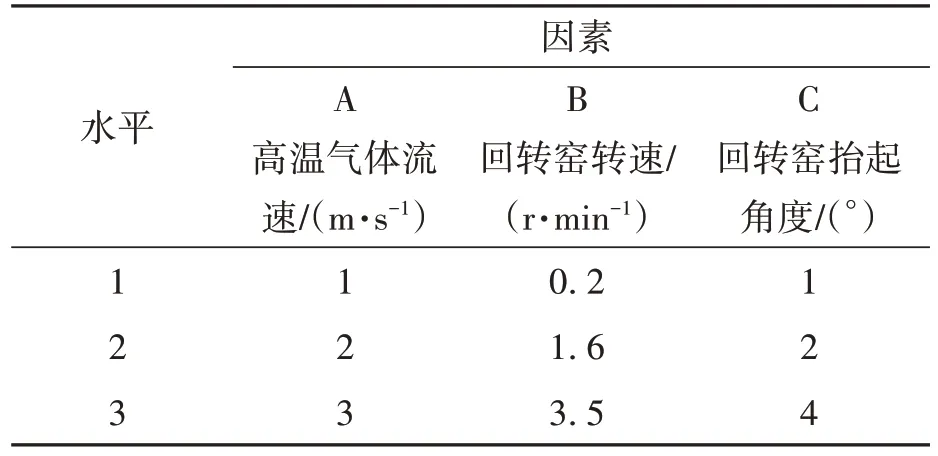
水平12 3因素A高温气体流速/(m·s-1)12 3 B回转窑转速/(r·min-1)0.21.63.5 C回转窑抬起角度/(°)12 4
3.2 正交试验分析
正交试验采用L9(34)正交表进行设计,试验方案及仿真结果数据如表3所示。
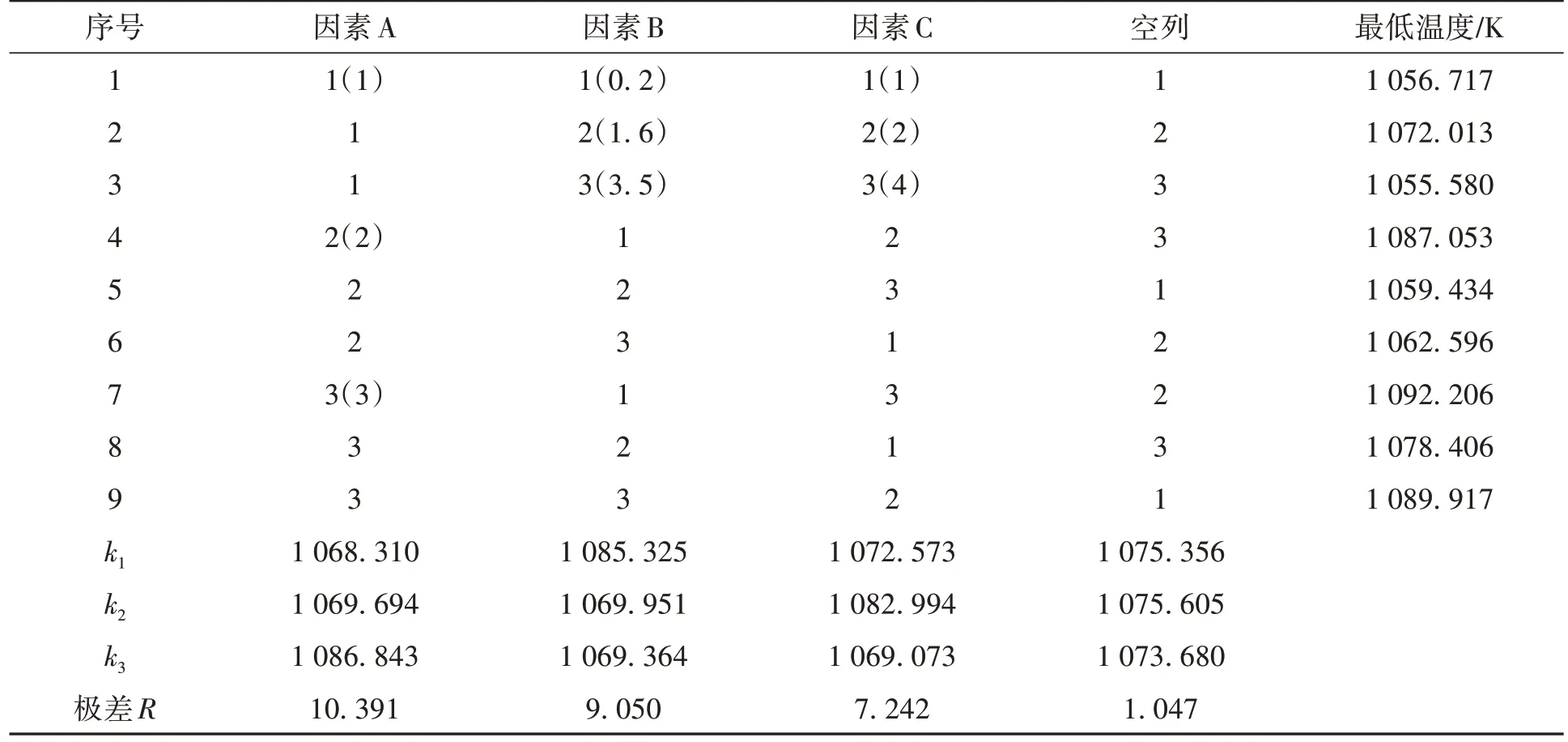
表3 正交试验方案及仿真结果Table 3 Orthogonal test scheme and simulation results
采用极差法分析正交试验结果,极差越大该因素对窑内最低温度的影响越大。由表3可知,极差R从大到小依次为R(A)、R(B)、R(C),因此,各因素的影响由大到小分别是高温气体流速、回转窑转速和回转窑抬起角度;各因素水平最佳组合为A3B1C2,即高温气体流速3 m/s、回转窑转速0.2 r/min、回转窑抬起角度2°时,窑内最低温度最高,窑内温差最小。
利用方差分析对上述结果进行验证,方差分析结果如表4所示。由表4可知,因素A对窑内最低温度的影响最为显著,因素C对窑内最低温度的影响最不显著,极差分析与方差分析结果一致。
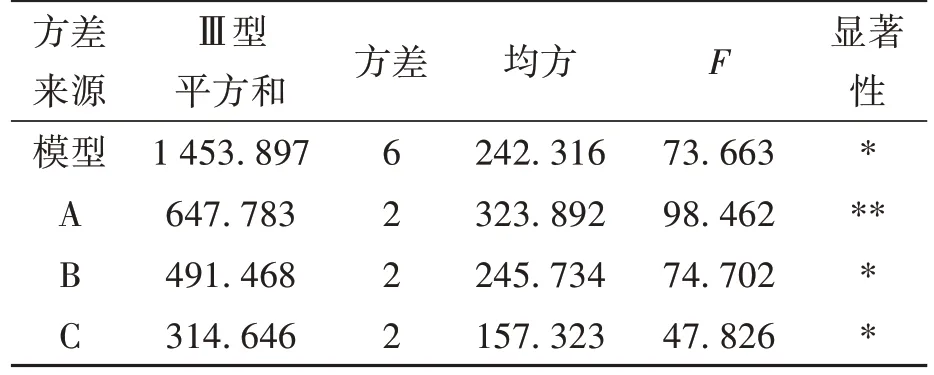
表4 方差分析表Table 4 Table of variance analysis
采用生产厂家初始方案(A1B1C1)时,窑内最低温度为1056.717 K,与窑内最高温度(1123 K)的温差为66.283 K;采用正交试验得到的最优方案(A3B1C2)时,窑内最低温度为1092.206 K,与窑内最高温度的温差为30.794 K;优化后,窑内最低温度提高了3.35%,温差下降了53.54%,有效改善了回转窑预热段温度分布不均的问题。
4 结论
本文采用正交试验进行仿真模拟,针对回转窑预热段传热问题进行研究,得出以下结论:
(1)由正交试验结果可以看出,影响回转窑预热段窑内最低温度的最显著因素为回转窑进气口高温气体的流速,其次为回转窑转速,最后是回转窑抬起角度。
(2)将优化后的方案与生产厂家初始方案进行比较可以发现,采用优化后的方案,回转窑预热段温度达到稳态时,窑内最低温度为1092.206 K,较初始方案提升了3.35%,与最高温度的温差为30.794 K,较初始方案下降了53.54%,改善了回转窑预热段窑内温度分布不均的问题。
