基于磁场解析和响应面模型的永磁电机优化

乔 峰，佟文明

基于磁场解析和响应面模型的永磁电机优化

乔 峰，佟文明

（国家稀土永磁电机工程技术研究中心（沈阳工业大学），沈阳 110870）

本文提出了一种基于混合磁场解析和响应面模型与遗传算法的内置式电机多目标优化设计方法，来实现电机的快速优化设计。本文将等效磁路法与精确子域法相结合，建立出电机空载和负载磁场解析模型，进而计算电机气隙磁密、反电动势以及电磁转矩，并通过有限元法与实验验证了解析模型的准确性。然后将混合磁场解析模型与响应面模型结合得出拟合回归方程，最后以电磁转矩平均值和永磁体体积为优化目标，采用遗传算法进行全局优化，从而获取电机最优方案。优化结果显示，优化后的内置式电机电磁转矩平均值增大了9.6％，永磁体体积减小了23％。

内置式永磁电机 混合磁场解析模型 响应面 多目标优化

0 引言

内置式永磁同步电机(Interior Permanent Magnet Synchronous Machine, IPMSM)具有高效率、高功率密度以及良好的弱磁扩速能力，在家用电器、军工装备、航天航空等领域具有广泛的应用[1]。与表贴式电机相比，IPMSM转子结构复杂，使得IPMSM的磁场计算以及优化设计更加困难。电机的多目标优化问题是在一定的限制条件下寻找一组电机各方面性能均优的设计模型。IPMSM多目标优化的方法多种多样，但是这些方法的都是根据电机参数和性能之间的关系来构建电机预测模型，再利用该模型对输出性能的变化来进行预测，最后通过算法寻优实现电机优化[2]。

田口法可对电机进行局部寻优，优化效果一般[3]，基于代理模型的优化可实现电机全局优化，但对于结构参数较多的优化问题，这种方法会变得较为复杂[4]。有限元方法对于各种复杂的定、转子结构能精确的计算电机的性能，但是基于有限元的算法寻优存在耗用时间久、计算成本高的问题[5]。解析法相比有限元法能够快速的实现电机性能计算，但是解析和优化算法的结合中存在大量迭代计算，依旧会花费很久的时间[6]。

本文提出一种基于混合磁场解析和响应面模型与NSGA-Ⅱ算法相结合的IPMSM多目标优化设计方法。该方法采用局部等效磁路考虑不同磁极结构转子表面磁势的变化，并与精确子域法相结合建立电机空载磁场解析模型；通过空载磁场与电枢磁场的叠加建立电机负载磁场解析模型，并采用麦克斯韦张量法对电机的电磁转矩进行计算。将经试验和有限元验证后的混合磁场解析模型应用于响应面模型中，再通过有限的试验之后得到的拟合回归方程，采用NSGA-Ⅱ算法，以电磁转矩平均值和永磁体体积为优化目标进行全局优化，最终获取电机的最优解。

1 混合磁场解析模型

本节采用了一种将等效磁路方法与子域法相结合的混合解析模型进行空载磁场计算。图1为磁场解析流程图，首先根据局部等效磁路建立不同磁极结构电机转子表面磁势表达式，然后通过麦克斯韦方程计算定子槽、槽隙和气隙内的磁场分布，根据标量磁势连续性和基尔霍夫定律，在极坐标下导出了两种方法之间的耦合边界条件。

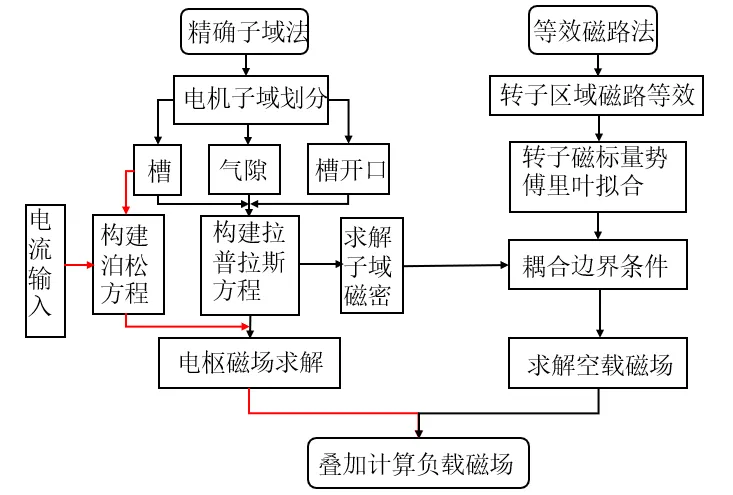
图1 磁场解析流程图

利用耦合边界条件得到的矩阵方程求解各待定系数，进而计算气隙中的磁场分布[7-8]。建立忽略转子结构的子域模型，添加电流激励，求解电枢磁场分布。

在负载状态下，由永磁体产生的磁通密度PM和电枢反应产生的磁通密度a叠加可得负载磁场，表达式为[9-10]：

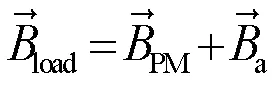
用麦克斯韦张量法求电磁转矩，表达式为：

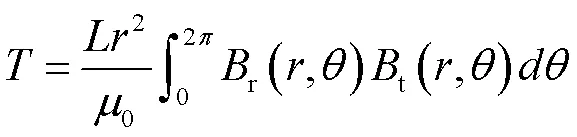
2 有限元验证及分析

本文对一台15 kW、20000 r/min、4极18槽的IPMSM进行计算，用有限元来验证解析计算的结果，包括空载气隙磁密、负载气隙磁密以及电磁转矩，电机的主要参数见表1。

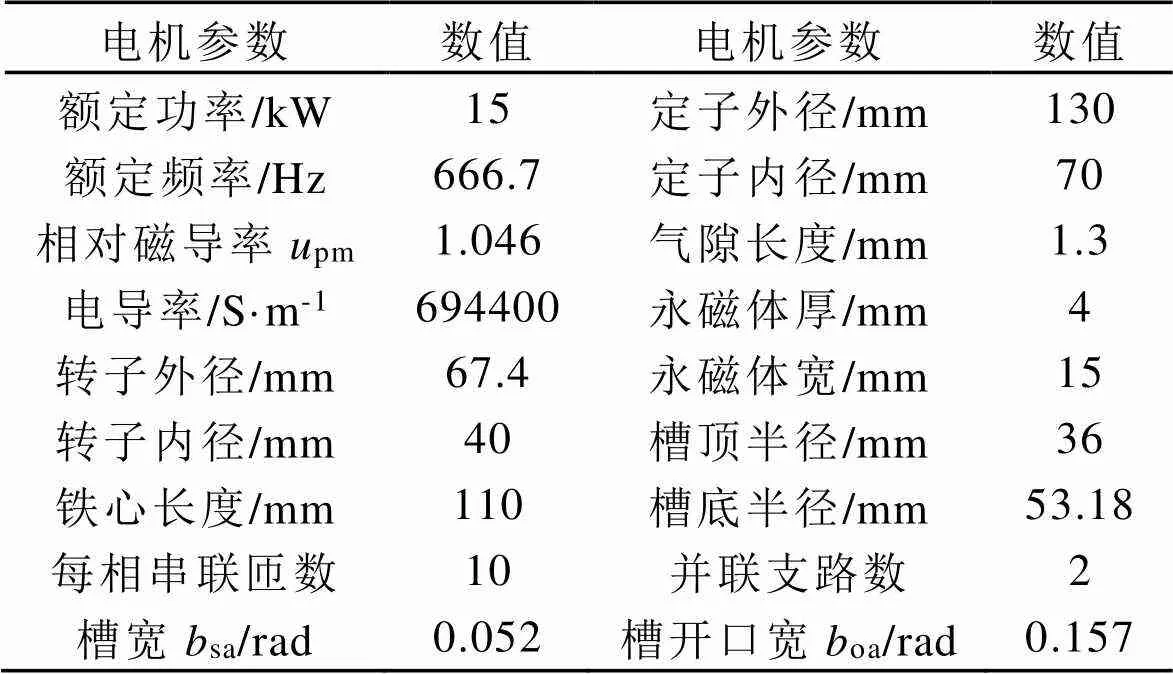
表1 电机主要参数

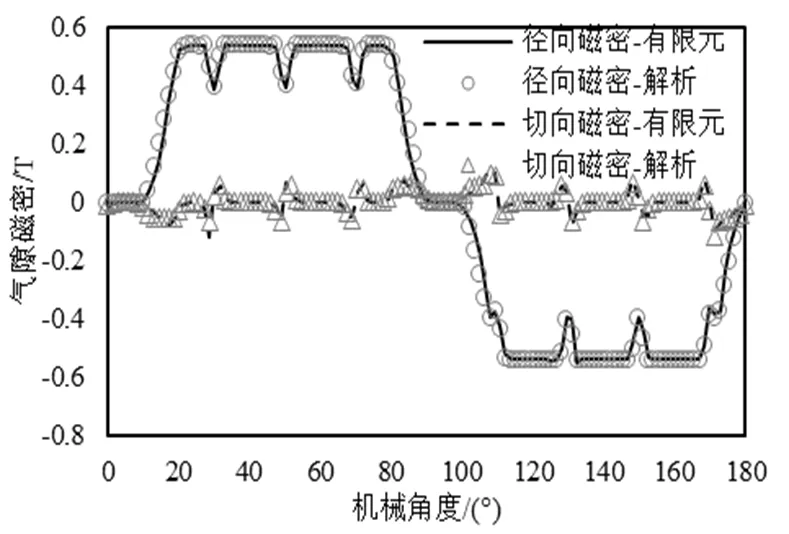
图2 空载磁场气隙磁密分布

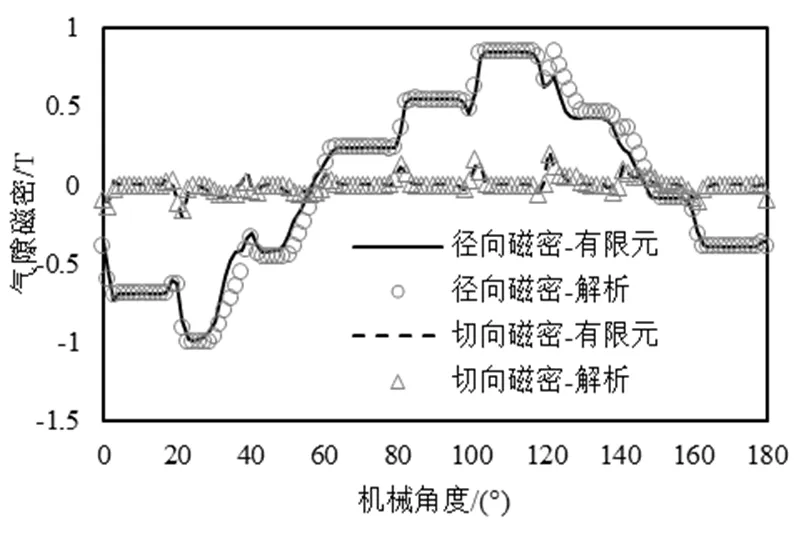
图3 负载气隙磁密分布

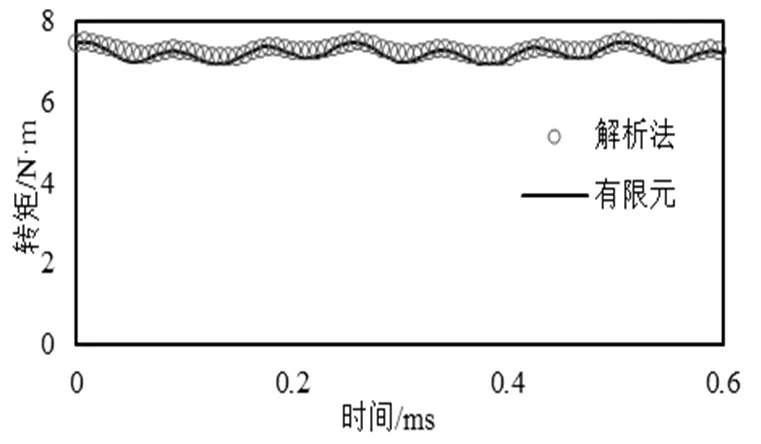
图4 电磁转矩

本文使用有限元软件建立电机二维模型，分别计算空载和负载状态时电机的气隙磁通密度，并且与解析结果进行了对比。

从图2、3、4可以看出解析结果和有限元结果的误差较小，比较吻合，验证了所用混合磁场解析模型的合理性。

3 实验验证

为了验证解析模型计算的准确性，搭建了如图5所示的样机实验平台。

图5 样机试验平台

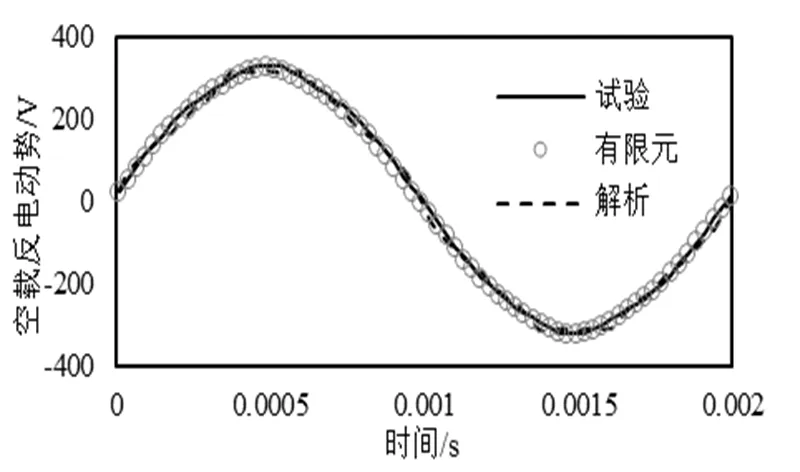
图6 电机空载反电动势结果比较

实验中测试了样机的空载反电动势以及负载特性，并将解析计算结果、有限元计算结果以及实验测试结果在图6进行了比较，可以看出，本文所使用解析方法计算结果与实验测试结果基本一致

4 多目标优化

内置式电机的转子结构复杂，优化过程中涉及到的参数较多，且参数之间相互关联，密不可分，往往改变一个参数就会影响多个参数，参数选择的不恰当不仅不能得到理想的优化结果，而且还会耗费大量的时间。考虑加工工艺的限制，如图7的转子中放置永磁体部分，留有约0.1 mm的径向空间。

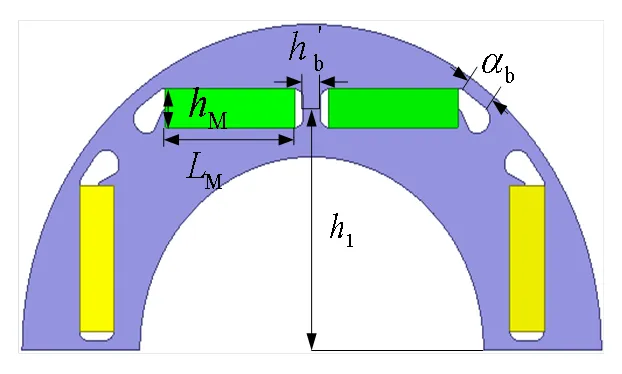
图7 转子结构参数

本次优化中将以电机的转矩平均值和永磁体体积为优化目标，在matlab软件中利用NSGA-Ⅱ进行多目标优化，优化流程如图8所示。

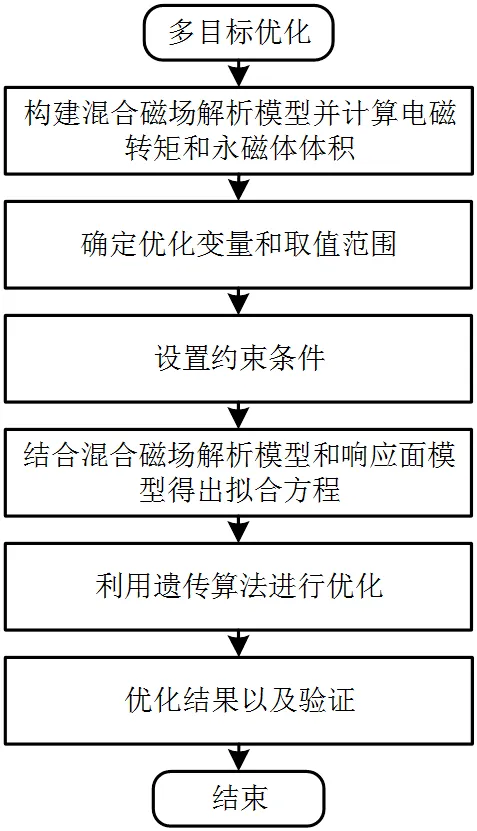
图8 多目标优化流程图

优化中所用永磁体材料为N42UH，剩磁密度为1.3T，矫顽力为989kA/m，并选择以下的结构参数为优化变量，其中包括：永磁体位置1，永磁体宽度M，永磁体厚度M，加强筋宽度’b以及隔磁桥厚度b，取值范围如表2所示。

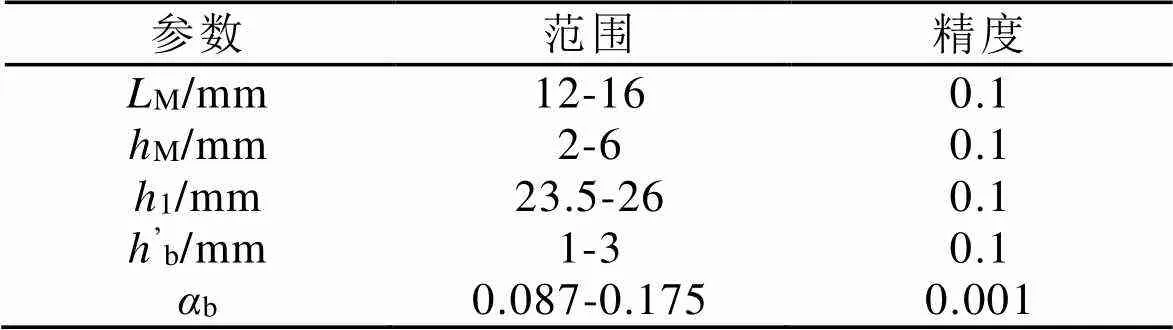
表2 优化变量及其取值范围

优化设计中，不仅需要优化目标和参数的选择，还需要设定约束条件，高速电机频率高，为了减少铁耗，所以其铁心磁密通常设计比较低，一般设计在铁心材料曲线膝点“△”附近。

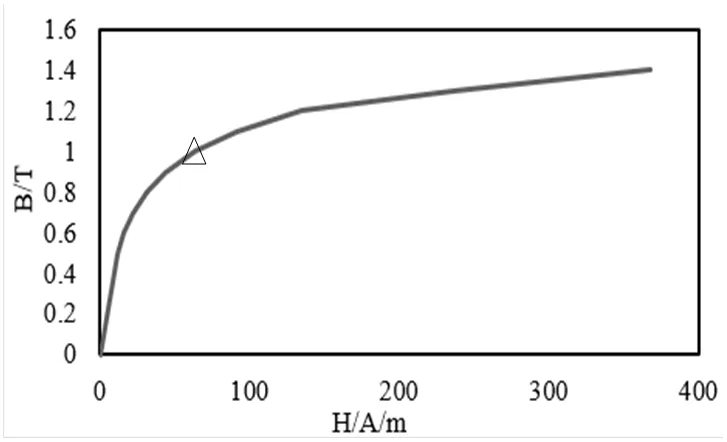
图9 非晶合金定子铁心B-H曲线

由图9可知膝点处磁密为1.1T，多目标优化的约束条件为：

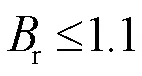
应用混合磁场解析进行响应面试验，试验结果经过拟合得出的回归方程为：

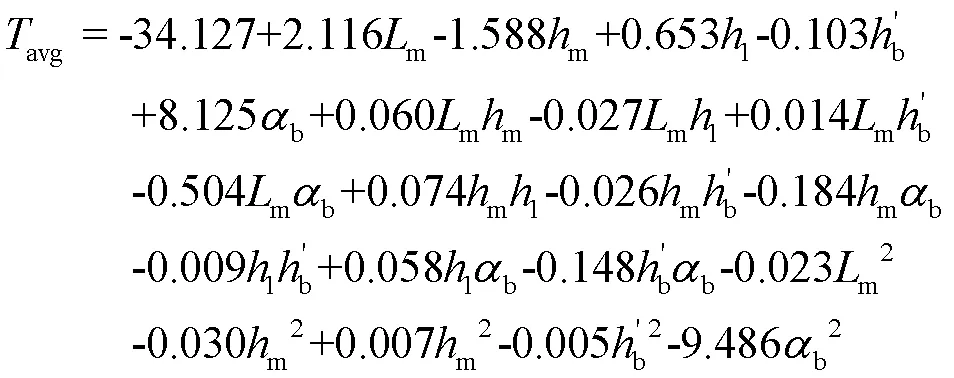
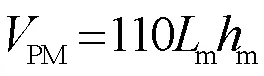
本文利用NSGA-Ⅱ进行寻优，优化结果如图10所示，所得的Pareto前沿中选择合适的点“○”来作为优化结果。

利用有限元软件对优化前后永磁电机进行了计算，电磁转矩平均值有明显的提升，如图11所示。

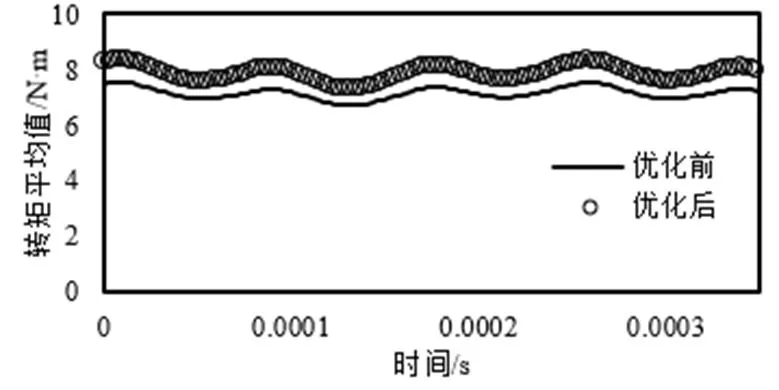
图11 优化前后转矩对比

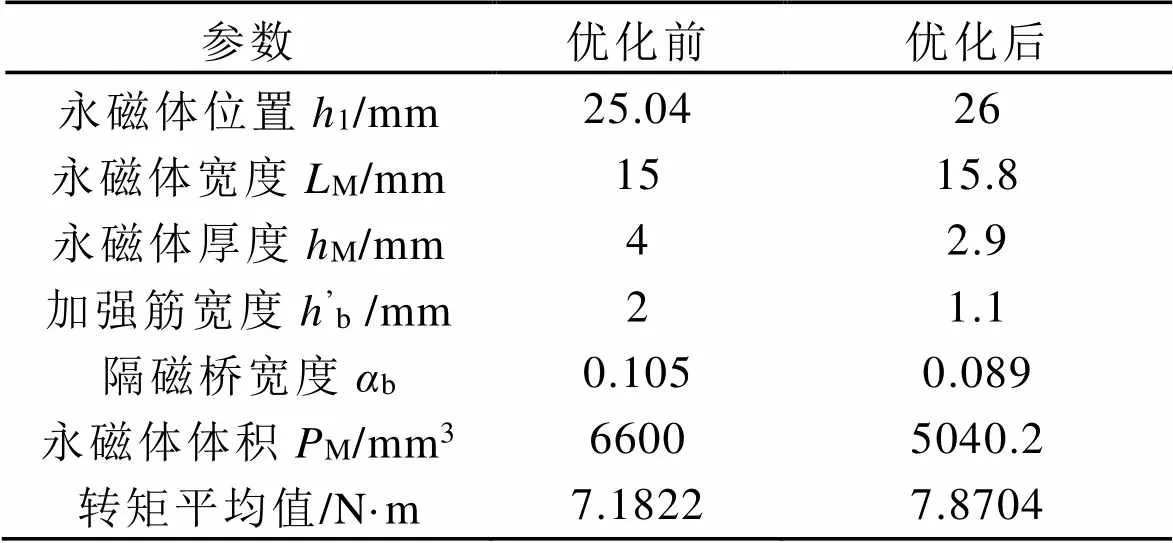
表3 多目标优化前后参数对比

表3为优化前后参数对比，加强筋宽度从2 mm减少到1.1 mm，考虑高转速下的转子结构强度，图12对优化后的电机进行应力分析，转子所受最大应力为261.6 MPa，小于转子材料412 MPa的屈服强度，电机可以安全运行。

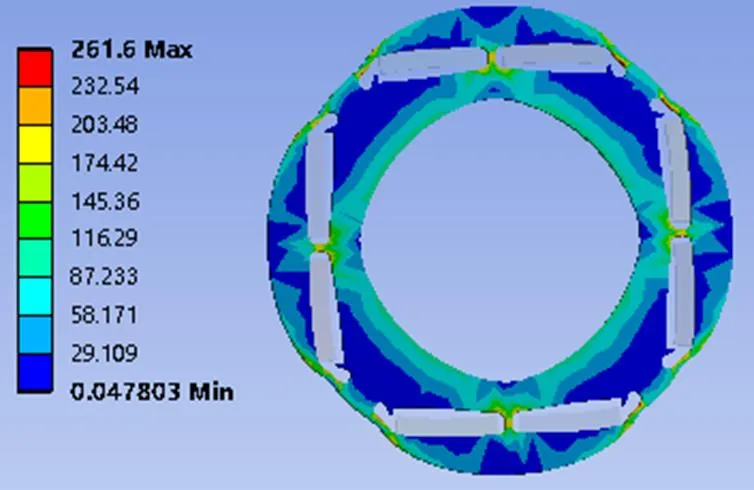
图12 转子应力分布图

永磁体厚度从4 mm减小到2.9 mm，考虑永磁体厚度减小导致工作点偏移，做出了如图13的永磁体磁密云图，永磁体磁密在0.9-1.1T左右，没有发生不可逆退磁。

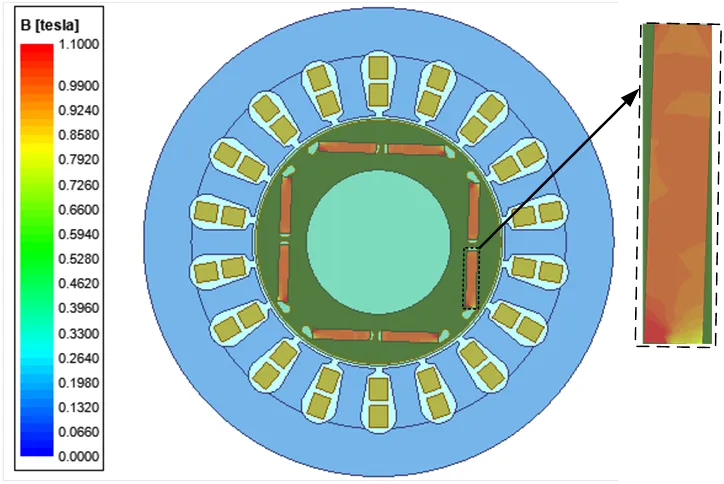
图13 永磁体磁密云图

优化前的转矩平均值为7.1822 N·m，优化后的转矩平均值为7.8704 N·m，转矩提升9.6%，增大了电机转矩密度。优化前的永磁体体积为6600 mm3，优化后的永磁体体积为5040.2 mm3，永磁体体积减小23.6%，节省了永磁体成本。

5 结论

本文采用局部等效磁路考虑不同磁极结构转子表面磁势的变化，并与精确子域法相结合建立了电机电磁性能的混合解析模型，并通过有限元以及实验验证了所提出的IPMSM磁场解析模型的准确性。将混合磁场解析模型与响应面模型相结合，得出拟合方程，再用NSGA-Ⅱ进行多目标全局优化，其中IPMSM电磁转矩平均值和永磁体体积为优化目标，优化后的电机转矩平均值提升9.6%，提高了电机转矩输出能力，永磁体体积减小23.6%，降低了永磁体用量，节省了成本。

本文所提出的基于混合磁场解析和响应面模型与NSGA-Ⅱ的IPMSM多目标优化设计方法，不仅避免了磁场解析和优化算法直接结合中，优化算法本身的大量迭代导致多次解析计算过程，节省计算时间，而且可实现任意极槽配合以及不同转子结构下的IPMSM的多目标快速优化，具有较强的通用性。

[1] 李维, 王慧敏, 张智峰, 等. 内置式永磁同步电机双层磁钢结构优化设计[J]. 天津工业大学学报, 2020, 39(06): 76-82.

[2] 郝金顺. 高功率密度永磁同步电机设计与多目标优化研究[D]. 中国地质大学(北京), 2020.

[3] Kim S I, Lee J Y, Kim Y K, et al. Optimization for reduction of torque ripple in interior permanent magnet motor by using the Taguchi method[J]. IEEE Transactions on Magnetics, 2005,41(5): 1796-1799.

[4] Du L. Liu X. Fu J, et al. Design and optimization of reverse salient permanent magnet synchronous motor based on controllable leakage flux[C]. CES Transactions on Electrical Machines and Systems, 2021,5(2): 163-173.

[5] Farshbaf R F, Vahedi A, Mirnikjoo S. Multi-Objective Optimization of Permanent Magnet Synchronous Motor Based on Sensitivity Analysis and Latin Hypercube Sampling assisted NSGAII[C]. Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), 2021: 1-5.

[6] 安原圣, 马琮淦, 李鑫, 等. 电动汽车用内置式永磁同步电机气隙磁场解析建模与多目标优化[J]. 中国公路学报, 2023, 36(01): 253-262.

[7] 沈月芬, 刘旭. 考虑互感的多齿开关磁链永磁记忆电机的精确磁路模型[J]. 电工技术学报, 2022, 37(10): 2435-2445.

[8] Wu L, Zhu Z, Staton D, et al. An Improved Subdomain Model for Predicting Magnetic Field of Surface-Mounted Permanent Magnet Machines Accounting for Tooth-Tips[J]. IEEE Transactions on Magnetics, 2011,47(6): 1693-1704.

[9] Guo B, Huang Y, Peng F, et al. A New Hybrid Method for Magnetic Field Calculation in IPMSM Accounting for Any Rotor Configuration[J]. IEEE Transactions on Industrial Electronics, 2019,66(7): 5015-5024.

[10] De B J, Sergeant P, Hemeida A, et al. Analytical Model for Combined Study of Magnet Demagnetization and Eccentricity Defects in Axial Flux Permanent Magnet Synchronous Machines[J]. IEEE Transactions on Magnetics, 2017,53(9): 1-12.

Optimization of permanent magnet motor based on magnetic field analysis and response surface model

Qiao Feng, Tong Wenming

(National Engineering Research Center for Rare Earth Permanent Magnet Machines Shenyang University of Technology,Shenyang 110870, China)

TM351

A

1003-4862（2023）08-0080-05

2023-02-27

乔峰（1996-），男，硕士。研究方向：高品质永磁及特种电机系统。E-mail：qqqqf2y@163.com