齿根等效应力的对比计算

2023-08-25何中石孟令宽

船电技术 2023年8期

何中石，孟令宽

齿根等效应力的对比计算

何中石，孟令宽

（湖南湘电动力有限公司，湖南湘潭 411101）

目前设计一般的齿轮传动时，通常只按保证齿根弯曲疲劳强度以及保证齿面接触疲劳强度两准则进行计算。由实践得知，对于齿面硬度很高，齿芯强度又低的齿轮或材质较脆的齿轮，通常则以保证齿根弯曲疲劳强度为主。本文针对一对齿轮副的齿根等效应力先后采用仿真分析计算方法；第四强度理论计算方法；齿根弯曲疲劳强度的经典计算方法来计算齿根等效应力。发现在本文所设置的载荷条件下，仿真分析计算的结果和齿根弯曲疲劳强度的经典计算方法所得的结果相近。

齿轮传动齿根等效应力第四强度理论齿根弯曲疲劳强度

0 引言

齿轮传动是机械传动中最重要的传动之一，形式很多，应用广泛，传递的功率可达数十万千瓦，圆周速度可达200 m/s。齿轮传动的主要特点有：效率高、结构紧凑、工作可靠、寿命长、传动比稳定。

轮齿折断是齿轮主要的失效形式之一。轮齿受载后，齿根处的弯曲应力较大，齿根过渡部分的形状突变及加工刀痕，还会在该处引起应力集中。在正常工况下，当齿根的循环弯曲应力超过其疲劳极限时，将在齿根处产生疲劳裂纹，裂纹逐步扩展，致使轮齿疲劳折断。

若使用不当造成齿轮过载时，齿轮在突加载荷作用下也可能出现折断；长期使用的齿轮因严重磨损而导致齿轮过分减薄时，也会在名义载荷下发生折断。

齿宽较小的直齿圆柱齿轮（简称直齿轮）一般发生整齿折断；齿宽较大的直齿轮，因制造装配误差使得载荷偏置于齿轮的一端，发生局部折断的可能性较大。斜齿圆柱齿轮（简称斜齿轮）和人字齿圆柱齿轮（或称人字齿轮）的接触线是倾斜的，齿轮受载后，如有载荷集中时，一般会发生局部折断。

对于齿轮齿根强度的计算，经典的计算方法为齿根弯曲疲劳强度计算。本文以一对直齿圆柱齿轮作为研究对象，先采用有限元方法计算齿根的等效应力，然后再根据载荷作用于齿顶时单个轮齿的受力情况，采用第四强度理论计算齿根的等效应力，最后采用齿根弯曲疲劳强度计算的经典方法，并分析对比以上三种计算方法的应力结果。

1 齿轮参数和齿轮建模

1.1 齿轮参数

本文所选择的齿轮副中的齿轮参数、安装信息和运行特点如下所示：齿数比=3.2；齿数：Z1=34、Z2=109；模数m=2；压力角=20°；齿宽：1=75、2=68；齿宽系数：Φd=1；中心距a=143 mm；齿根圆角：1=0.76、2=0.76[1]；圆周速度：=2.1 m/s；齿轮精度：=7；齿轮布置方式为对称布置；小齿轮为主动轮（硬齿面），大齿轮为从动轮（软齿面）；小齿轮的输出扭矩为1=9.948×104N·mm且载荷状态均匀平稳。

1.2 齿轮的建模

根据1.1中的齿轮参数，利用SolidWorks三维建模软件对小齿轮和大齿轮分别进行建模。在建模过程中将齿宽统一为6.8 mm（该齿宽为大齿轮实际齿宽的0.1倍，因扭矩与齿根受力大小呈线性关系，在后续加载载荷时仅取实际扭矩的0.1倍），并且在建模时扩大齿轮内孔尺寸，以减少后续仿真分析计算时的网格数量尽量节省计算资源。

根据《齿轮手册》[2]可知，齿轮在啮合时，当载荷作用在单对齿啮合区的最高点时，齿根产生的弯曲应力最大。本文中选择大齿轮中某一齿的齿根强度进行分析。则在建模过程中需要将小齿轮某一齿面进行投影并分割，其分割线恰好能够与大齿轮齿顶圆和齿面渐开线相交形成的棱边接触。小齿轮建模后的外形如图1所示；大齿轮建模后的外形如图2所示；齿轮啮合处及齿根弯曲应力校核位置如图3所示。

图2 大齿轮

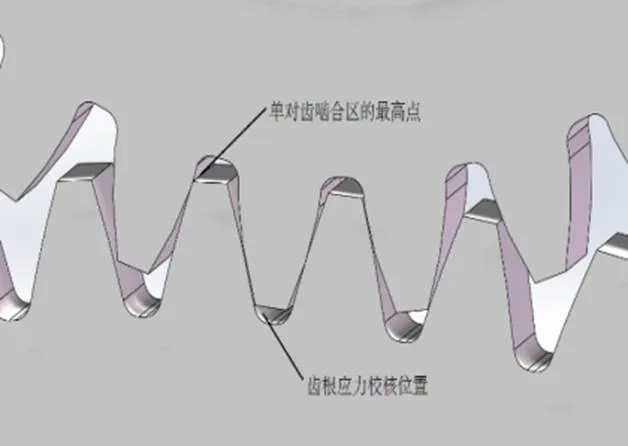
图3 齿轮啮合处及齿根弯曲应力校核位置

2 仿真分析计算[3]

2.1 仿真模型及前处理

将第1章中的三维模型保存为igs格式后导入AnsysWorkbench并采用Static Structural模块进行分析。在进入到分析模式之前，需将模型在DesignModeler模式下将二齿轮模型内孔面进行合并，以方便后续边界条件的设置以及载荷的加载。

2.2 网格的设置

由于在分析模型中，两齿轮的厚度均为6.8 mm，两齿轮模型的网格大小设置为2.5 mm。由于最大受力位置为啮合区最高点的齿轮根部（本文选择的是大齿轮根部），所以在该处大齿轮根部的网格设置为0.1 mm以确保计算精度。所有网格均选择四面体网格即Tetrahedrons即可。齿轮啮合位置的网格如图4所示，该图中已隐藏小齿轮。此时网格节点数为635768，单元数为428921。

图4 啮合区最高点大齿轮根部网格

2.3 载荷的加载以及边界条件的设置

设置边界条件时将大齿轮作为受力物体，其内圈面设置成Fixed Support，同时以小齿轮内圈面为基准，建立一个Coordinate System并将Y方向自由度定义为齿轮旋转方向的自由度。在小齿轮内圈面设置Displacement的约束，其中X和Z方向的位移设置为0，Y方向的位移设置为Free，如图5所示。最后在小齿轮内圈面施加扭矩载荷即Moment，载荷大小为9948N·mm（因为齿轮厚度为实际参数的0.1倍所以扭矩载荷也为实际参数的0.1倍）。

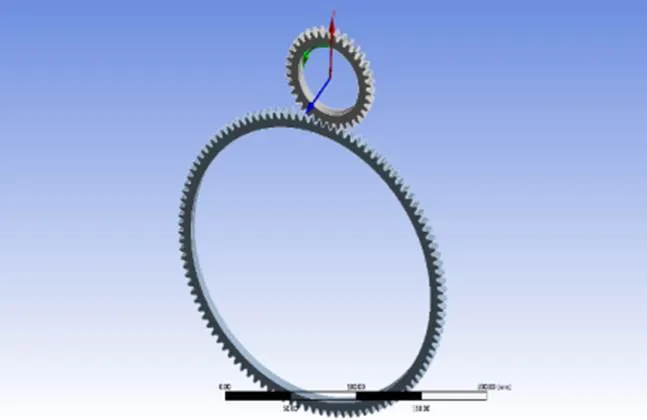
图5 小齿轮内圈Coordinate System的建立

在接触对的设置时删除掉原系统自动生成的接触对后，手动添加啮合区最高点为唯一的接触对。其小齿轮渐开线面为接触面，大齿轮渐开线面及齿顶圆面为目标面。接触形式选择无摩擦接触以忽略摩擦力对计算结果的影响。具体见图6、图7所示：

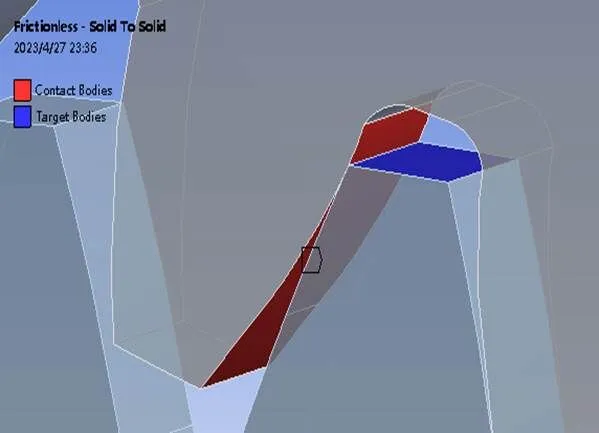
图6 齿轮接触对位置

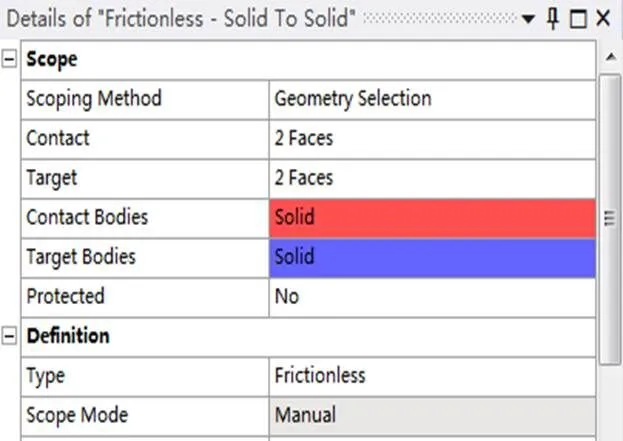
图7 齿轮接触对形式设置

2.4 仿真分析计算结果

经仿真分析计算，大齿轮根部的最大等效应力为93.1 MPa,最大应力位置出现在啮合区最高点大齿轮受压一侧的根部，如图8所示。受拉一侧的根部的等效应力相对较小为79.5 MPa，如图9所示。

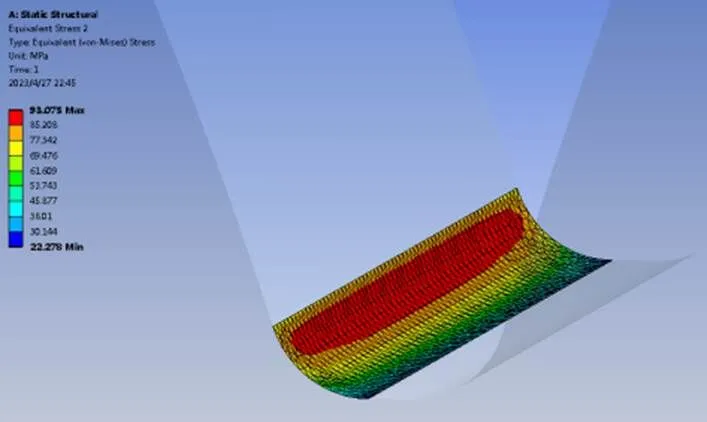
图8 大齿轮根部最大应力位置

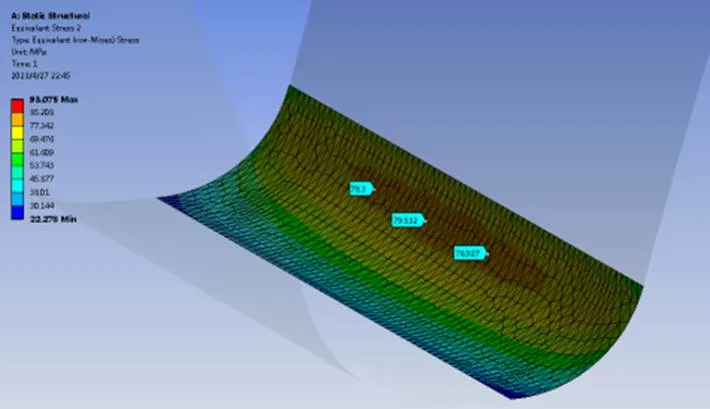
图9 大齿轮根部受拉一侧最大应力

为与后续经典计算进行对比，现提取齿轮啮合区最高点大齿轮对小齿轮的反力Force Reaction，如图10、图11所示：

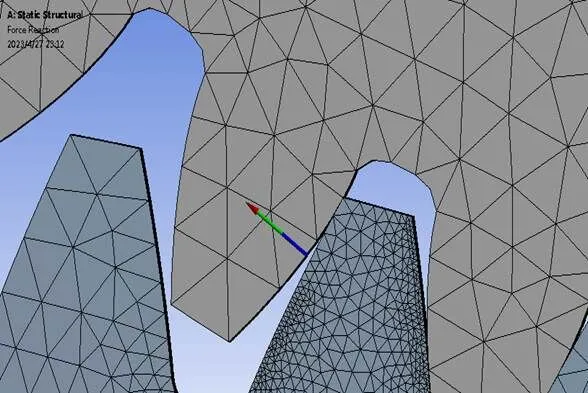
图10 啮合区最高点大齿轮对小齿轮反力

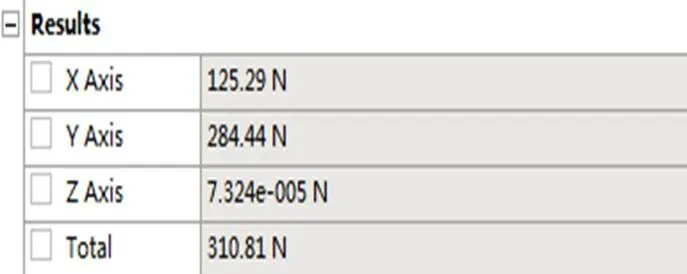
图11 啮合区最高点反力值

通过上述计算可知齿轮啮合区最高点大齿轮对小齿轮的反力为311 N。

3 根据第四强度理论计算齿根的等效应力

3.1 经典力学计算过程中力的解析

载荷作用于齿顶时的情况如图12所示。图中，γ为载荷作用于大齿轮齿顶时的压力角，载荷Fn可以分为Fncosγ和Fnsinγ两个分量，其中，前者在齿根产生弯曲应力σF0和剪应力τF0，后者在齿根产生压应力σc0。齿根弯曲应力的危险截面可用30°切线法确定，如图13所示。图中，与轮齿对称线成30°角，并与齿根过渡曲线相切的两条直线，切点分别为A、B，线段AB表示的就是齿根处的危险截面。该处的弯曲应力σF0、剪应力τF0和压应力σc0的计算公式分别为：

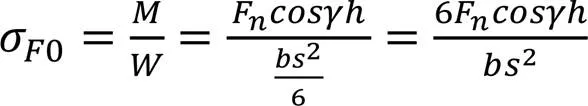
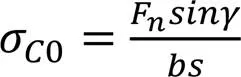
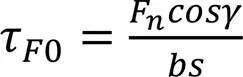
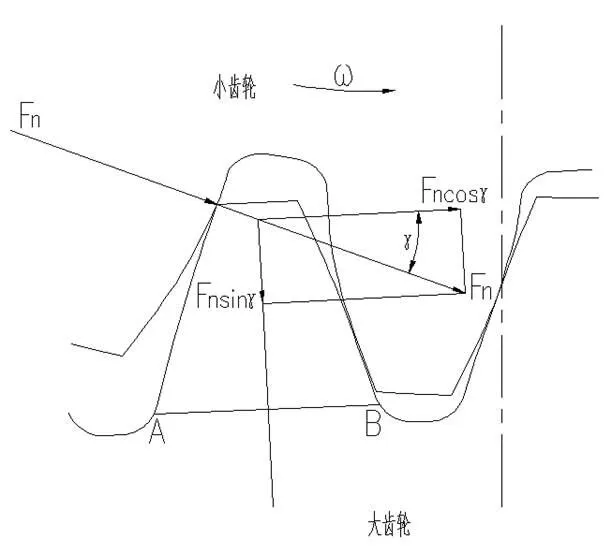
图12 载荷作用于齿顶时力的解析

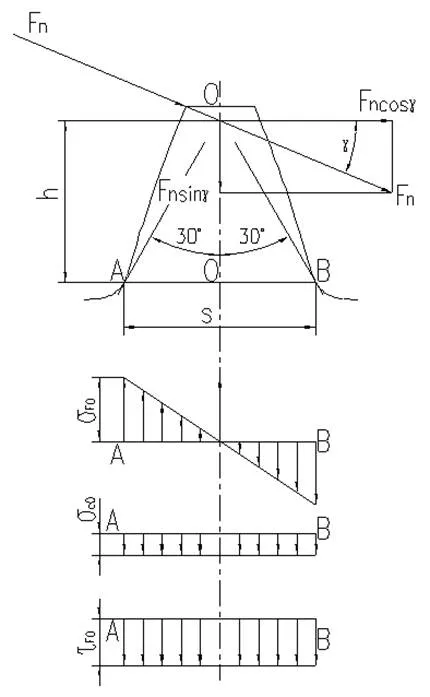
图13 齿根处的弯曲应力、压应力和剪应力

3.2 各参数值的确定

图12、图13中与齿轮相关参数的确定如下：γ为齿顶圆压力角，其计算公式为：

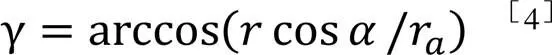
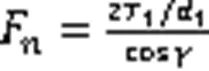
根据Fn的计算结果，对比仿真分析中大齿轮对小齿轮计算得到的反力（311N），可知该二结果计算的误差在2%左右。

3.3 计算过程

经过上述计算，各基本参数已经确定，现将各参数分别代入3.1节中的公式（1）、（2）、（3），具体如下所示：

齿轮单个齿在受力时可视为悬臂梁[6]，根据材料力学的知识齿根圆角处的剪应力约等于0，但此处本文仍然取AB横截面的平均剪应力进行计算）下面根据第四强度理论［7］计算齿根部位的等效应力，此处以图13中沿O-O轴方向（竖直方向）的应力定义为σ1，与纸面方向相切同时又垂直于O-O轴方向的应力定义为σ2，垂直于纸面方向的应力定义为σ3。此时可得：

σ1=σF0+σC0=48.4+4=52.4（MPa）

σ2=τF0=9.6（MPa）

σ3=0（MPa）

将上述计算结果代入到第四强度理论计算齿轮根部的等效应力：

4 采用齿根弯曲疲劳强度的经典计算方法

采用齿根弯曲疲劳强度的公式进行计算时即分别通过应力修正系数Ysa、重合度系数Yε和载荷系数KF对齿根部位的弯曲应力σF0进行修正。齿轮齿根弯曲疲劳强度的计算公式为：

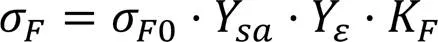
式（5）中的σF0=48.4MPa在3.3节中已经得出。应力修正系数Ysa可根据1.1节中给出的参数通过查阅图表的方法得出Ysa≈1.82。当然也可以通过公式（6）[8]对应力修正系数Ysa进行计算。：

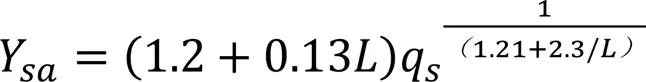
SFn—齿根危险截面齿厚；

hFe—弯曲力臂

ρF—30°切线切点处的曲率半径

笔者采用该公式计算大齿轮的应力修正系数Ysa≈1.90，计算过程在此不再赘述。

载荷系数KF的值是由使用系数KA、动载系数KV、分配系数KFα以及分布系数KFβ的连续乘积得到。

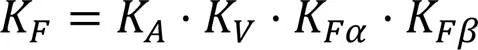
根据1.1节中给出的参数可以通过查阅图表的方法得出：KA=1.0、KV=1.08、KFα=1.2、KFβ=1.34。（应力修正系数Ysa、使用系数KA、动载系数KV、分配系数KFα、分布系数KFβ均可以通过机械设计教材、机械设计手册或齿轮手册查阅到）

则载荷系数为：

重合度系数Yε的计算公式为：

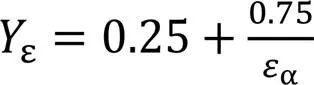
（8）中的εα为齿轮的重合度，其计算公式为：

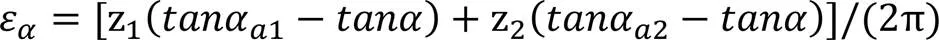
（9）式中的αa1和αa2分别为小齿轮和大齿轮齿顶圆压力角，其中大齿轮齿顶圆压力角已经在第3.2节中得到（αa2≈22.8°即（4）中的γ）。现将小齿轮分度圆半径r1=34 mm、齿顶圆半径ra2=36 mm、压力角α=20°代入公式（4）中可得小齿轮齿顶圆压力角αa1≈27.4°。将上述已知数据带入到（9）中可得：

可得重合度系数Yε≈0.66。将以上所得数据带入到式（5）中可得：

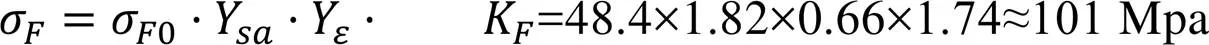
5 结论

根据以上计算结果可知，仿真分析计算的齿根等效应力为93.1 MPa；根据第四强度理论计算的齿根等效应力为47.8 MPa；采用齿根弯曲疲劳强度的计算方法得到的弯曲疲劳应力为101 MPa。综合对比上述三种计算方法得到的结果可以发现，仿真分析计算和齿根弯曲疲劳强度计算得到的应力结果相近，可见按照本文所设置的边界条件用仿真分析计算的方法得到的齿根等效应力已经有一定的安全冗余，其等效应力值略小于在1.1节中的齿轮相关参数条件下的弯曲疲劳应力值，具有一定的计算精度，其相对于弯曲疲劳应力值误差在8%左右。

[1] 张云秀，韩志引，李东艳.航空直齿轮轮缘厚度对齿根应力的影响规律[J]. 机床与液压，2020(21)：176-181.

[2] 齿轮手册编委会. 齿轮手册. 北京：机械工业出版社. 1990.

[3] 周炬. 苏金英. ANSYS Workbench有限元分析实例详解（静力学）[M]. 北京: 人民邮电出版社. 2018.

[4] 西北工业大学机械原理及机械零件教研室. 机械原理[M]. 北京: 高等教育出版社.

[5] 西北工业大学机械原理及机械零件教研室.机械设计[M]. 北京: 高等教育出版社. 2013.

[6] 冯守卫，濮良贵，张少名，王守宇. 关于齿根应力计算方法的建议[J]. 齿轮, 1989（2）: 50-53.

[7] 孙训芳，方孝淑，关来泰，材料力学（Ⅰ）[M]. 北京：高等教育出版社. 2009.

[8] 机械设计手册编委会. 机械设计手册. 第2卷. 北京: 机械工业出版社. 2015.

Comparative calculation of equivalent stress at tooth root

He Zhongshi，Meng Lingkuan

(Xiangtan Electric Manufacturing Group Co., Ltd, Xiangtan 411101, Hunan，China)

TH123.4