孤立波低顶海堤越浪的数值模拟研究

刘竹琴，殷铭简，赵西增，2，罗 敏

（1.浙江大学 海洋学院，浙江 舟山 316021；2.浙江海洋大学 海洋工程装备学院，浙江 舟山 316022）

随着全球气候变化，灾害性海浪（台风浪、海啸等）发生的频率和强度呈上升趋势。图1为强台风“烟花”登录浙江温岭产生的灾害性台风浪［1］，其引发的越浪对海岸附近人员安全造成严重威胁，诱发的海水倒灌对海岸及岸后结构物造成严重破坏，使得海防工程承受越来越大的风险。

图1 强台风“烟花”登陆浙江温岭[1]（图片来源：https://new.qq.com/rain/a/20210723A02VJ700）Fig.1 Severe Typhoon In-Fa landing in Wenling, Zhejiang[1]（Source：https://new.qq.com/rain/a/20210723A02VJ700）

浙江沿海地区普遍采用海堤来防止海浪的破坏性作用（如越浪和剧烈波浪撞击）。在常规海浪情况下，海堤可以对海岸起到很好的防护作用。然而在台风期间，风暴潮导致水面上升，使得现役海堤堤顶高度减小，转变为低顶结构（即按EurOtop（2018）［2］定义，相对超高为0 ≤Rc/H0< 1.5的状态），无法有效防止越浪；此外，剧烈海浪撞击海堤，产生巨大荷载，对海堤结构、附近基础设施和人员安全造成严重威胁。

孤立波被广泛应用于模拟长波等灾害性海浪在浅水中的运动［3］。孤立波经过海堤产生的越浪量和波浪力是目前评判越浪作用机制的主要参数。对于孤立波越浪量经验公式的研究，Ozhan 和Yalgmer［4］试验研究孤立波经过坡面较陡的三角海堤的爬高和越浪量，并基于堰流比拟的方法提出了越浪量经验公式，但不具有普适性；目前国内外普遍认可的经验公式为Baldock等［5］通过大量试验研究总结得到的孤立波爬高和越浪量经验公式，研究表明越浪量与爬高具有较高相关性，因此在计算越浪量时需采用爬高数据；随后，张金牛［6］试验研究孤立波经过梯形海堤越浪量，提出的经验公式依赖于相对波高（0.144 ≤H0/h0≤ 0.607）和相对超高（0.165 ≤Rc/H0≤ 2.649）；此外，Lee 等［7］通过物理模型试验得到孤立波经过垂直护岸和斜坡护岸的越浪量经验公式；魏斐斐等［8］采用FLUENT 软件，模拟孤立波经过斜坡堤的越浪，并总结出越浪量沿堤顶宽度衰减的经验公式。越浪量是海堤工程设计中的一个关键因素，国内外学者对该物理量开展了大量研究，并提出如下关于孤立波越浪量的经验公式：

1）Baldock 等［5］通过物理模型试验，综合分析试验数据以及前人研究成果，认为孤立波的越浪量受爬高和堤顶超高的影响，得到计算孤立波爬高和越浪量的经验公式：

式中：q为孤立波的单宽越浪量；H为波高；d为水深；R为孤立波的爬高；Rc为堤顶超高；q0表示孤立波在传播时相对于静水面的孤立波水体体积，其计算公式见式（17）。该公式在计算越浪量时需采用爬高数据。

2）张金牛［6］通过物理模型试验，研究不同水深和波高下孤立波经过梯形海堤的越浪量，认为越浪量与相对波高和相对超高有关，采用Baldock 等［5］方法对其进行无量纲化，得到经验公式，该公式适用范围为0.165 ≤Rc/H≤ 2.649。

Baldock等［5］提出的经验公式需先计算孤立波的爬高，再通过爬高计算越浪量，较为繁琐，不能通过水深和波高数据进行直接求解；张金牛［6］提出的公式相对超高适用范围为0.165 ≤Rc/H≤ 2.649，不适用于0 ≤Rc/H≤ 0.164。且我国《海堤工程设计规范》（GB/T 51015—2014）［9］以及EurOtop（2018）规范［2］缺少计算孤立波越浪量经验公式。因此，文中研究旨在填补孤立波在低顶海堤下越浪量经验公式的空白。

对于波浪力的研究，Hsiao 和Lin［10］研究3 种相对波高的孤立波经过位于斜坡海岸上海堤的越浪形态及其在海堤两侧产生的波浪力，并分析孤立波在海堤后方的涡流运动与卷入气体的关系，试验数据可用于校准数值模型。其中，Tsung 等［11］以Hsiao 和Lin［10］的研究为基准算例，采用高阶Boussinesq 方程研究不同水深下孤立波经过不透水海堤产生的波浪力和越浪量，并讨论斜坡坡度以及波浪非线性作用的影响；此外，Luo等［12］也以Hsiao 和Lin［10］的研究为基准算例，采用CPM 模型模拟孤立波经过海堤时产生的波浪力和越浪量，并讨论海堤前坡坡度对越浪的影响。但未具体讨论孤立波作用在海堤两侧波浪力与相关参数的变化规律，对此需开展进一步研究。

基于上述背景，文中采用已被证实能够有效模拟波浪与结构物作用的开源程序OpenFOAM 中interFoam求解器［13］，以浙江沿海普遍采用的斜坡堤海堤断面型式为原型，考虑一种代表性长波即孤立波，研究孤立波在不同波高、水深和堤顶超高下的越浪过程，揭示越浪机理，总结出适用于低顶海堤的孤立波越浪量经验公式。并探究防浪墙高度对越浪特征的影响以及防浪墙所受波浪力的变化，综合考虑防浪墙减少越浪以及自身所受波浪力，给出建议的防浪墙高度。

1 数值模型理论和方法

采用OpenFOAM 中的两相流求解器interFoam，求解雷诺时均连续性方程和Navier-Stokes 方程，采用有限体积法（finite volume method）进行数值离散，模拟水体和空气两相不可压缩流体的运动。

式中：μ为动力黏度，k为湍流动能，δij为克罗内克符号，υt为湍流运动黏度。

采用流体体积（VOF）法追踪自由液面。定义体积分数α，α= 1 表示该单元充满水，α= 0 表示该单元充满空气，α介于0和1之间表示单元中既有空气又有水。通过求解α的输运方程，即式（8）来追踪自由液面：

为修正尖锐表面，且限制α的取值在0和1之间，引入人工压缩项对式（8）进行修正：

式中：uc为压缩速度，uc，i= min(cα|ui|，max|ui|)，其中cα是控制交界面压缩程度的参数，这里取值为1［13］。该人工压缩项是守恒的，且在全是水或空气时取值为0，即只在水体与空气的交界面处生效。

基于体积分数α的加权值计算得到每个单元内流体的密度ρ：

式中：ρwater和ρair分别表示水和空气的密度。

文中模拟采用Devolder等［14］建立的浮力修正SST k−ω湍流模型，基本方程为：

式中：k为湍动能，ω为耗散率，υ为流体的运动黏度，S为流体的平均应变率；β*= 0.09；a1= 0.31；F1和F2为计算σω、σk、β和γ所用到的参数，取值详见Devolder等［14］研究。

2 数值模型验证

2.1 模型设置

通过模拟具有试验［10］和数值基准数据的孤立波与海堤相互作用的算例来验证所采用的数值模型的准确性。二维数值波浪水槽的计算域如图2所示，水槽长22 m，高0.4 m。水槽左侧为造波区，在距离造波边界7 m处有一坡度比为1∶20的斜坡，在距离造波边界10.6 m处的斜坡上有一个海堤。在海堤前、后坡不同位置处放置压强测点用于记录海堤上的波浪动压强，并在数值水槽代表位置放置浪高仪用于测量波高。用于测量波高的浪高仪和动压强的测点的位置如图2所示，其详细位置如表1和表2所示。选取Hsiao和Lin［10］研究中水深h0=0.256 m、波高H0=0.058 9 m（波陡ε=H0/h0=0.23）的孤立波工况进行模拟。

表1 浪高仪位置Tab.1 Positions of wave gages

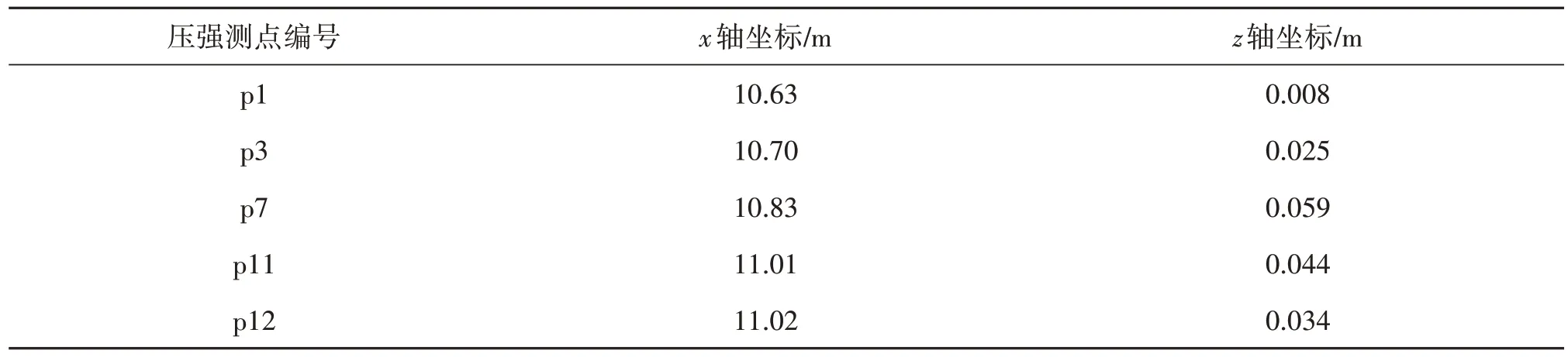
表2 压强测点坐标位置Tab.2 Positions of pressure sensors

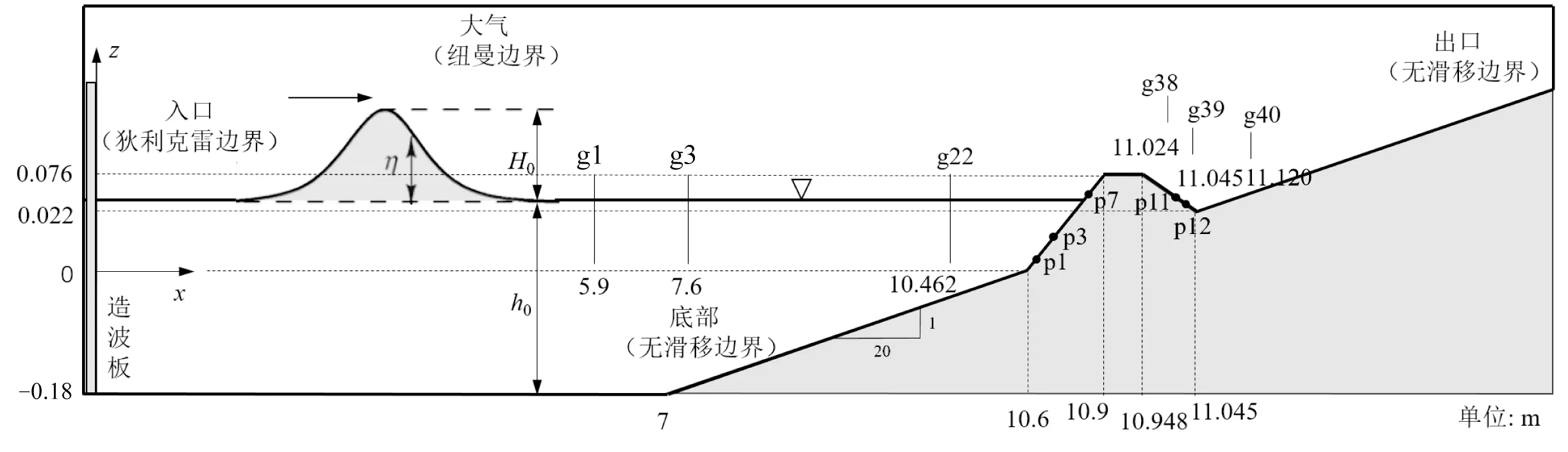
图2 计算域尺寸、浪高仪和压强测点位置以及边界条件Fig.2 Dimensions of computational domain, positions of wave gauges and pressure sensors and boundary conditions

关于计算边界，计算域底部（包括结构物表面）和出口采用无滑移边界，计算域顶部采用零梯度边界，计算域入口采用速度边界法产生孤立波。文中采用一阶孤立波公式，波面方程η为：

2.2 收敛性分析

采用3套网格进行网格收敛性验证，分别为细网格、中网格、粗网格，3套网格参数信息见表3，均采用自适应时间步，库朗数上限为0.25。不同网格尺寸下的g22处波高历时曲线如图3所示，p7处动压强历时曲线如图4所示。模拟结果表明，粗网格下的波高和压强结果明显比其他两组数值结果偏小，中网格和细网格下的数值结果趋于一致。对于中网格，进行时间步长收敛性分析，图5 和图6 分别为库朗数上限为0.10、0.25、0.50 下g22 处波高历时曲线和p7 处动压强历时曲线结果对比，由图可知库朗数上限0.10 与0.25 结果趋于一致，库朗数上限0.50 模拟结果偏小。综合考虑数值模拟精度和效率，选取中网格尺寸以及库朗数上限0.25开展模拟研究。

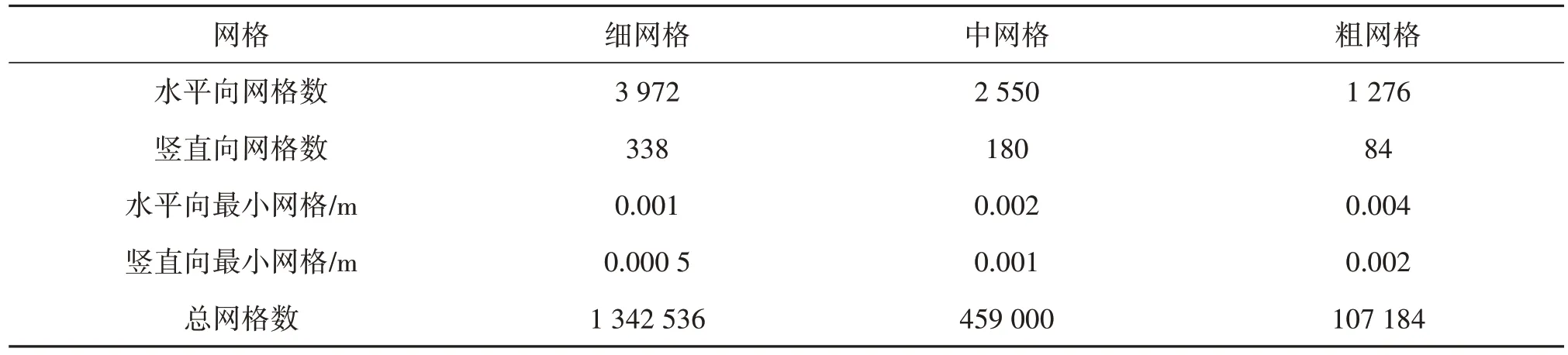
表3 收敛性验证网格信息Tab.3 Convergence verification grid information

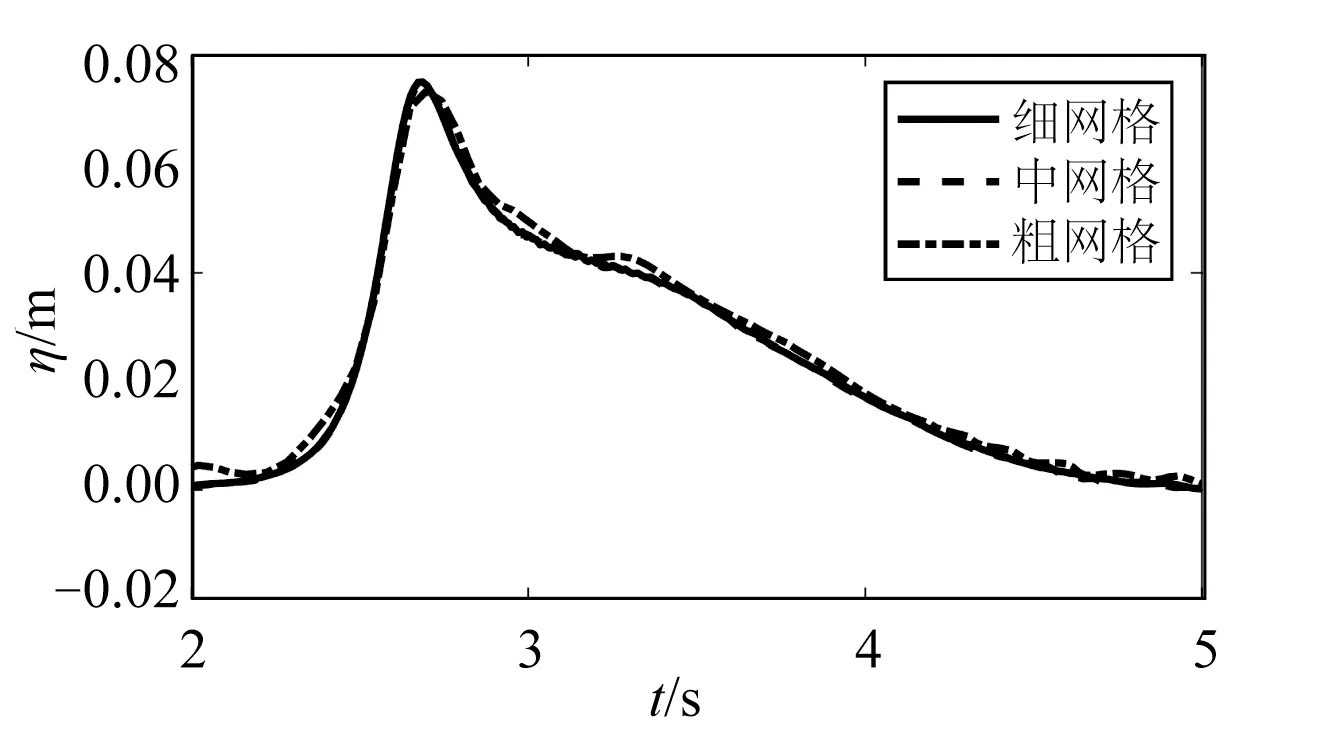
图3 不同网格尺寸下g22处波高历时曲线Fig.3 Wave elevations at g22 under different grid sizes

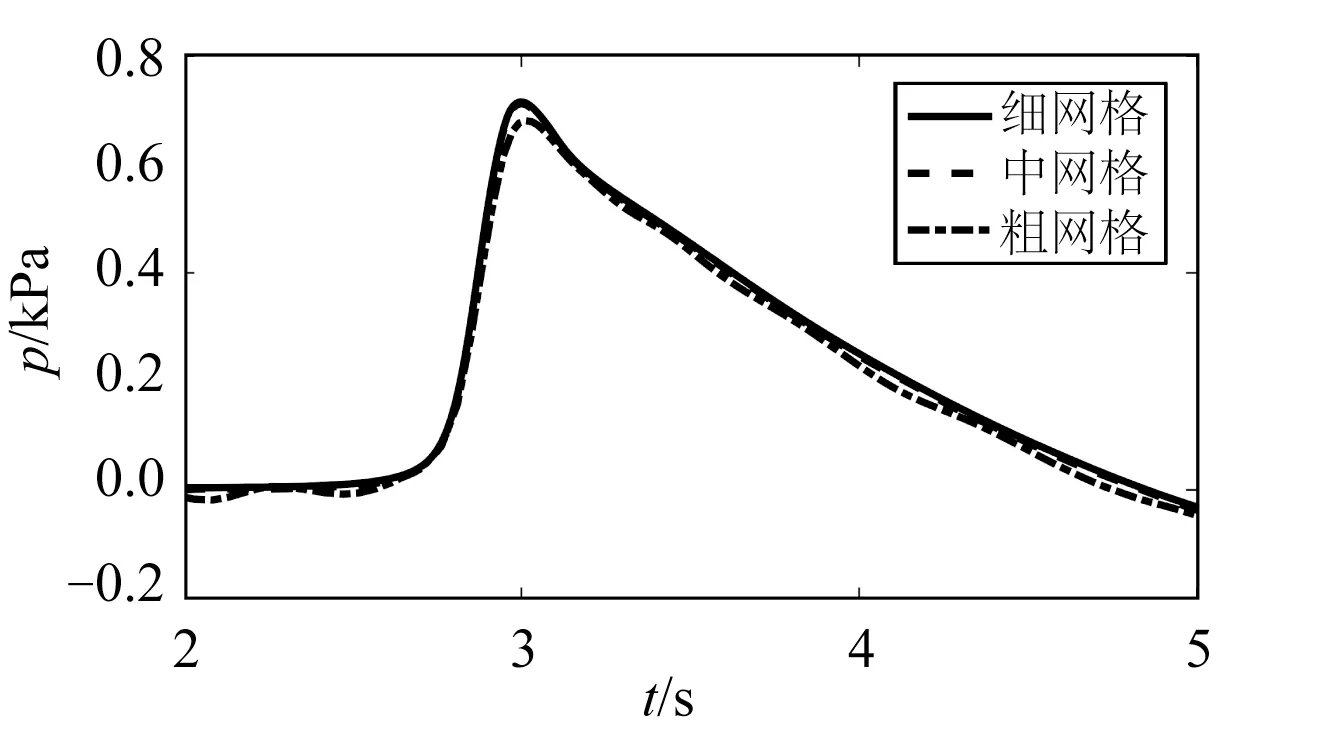
图4 不同网格尺寸下p7动压强历时曲线Fig.4 Dynamic pressures at p7 of the seawall under different grid sizes

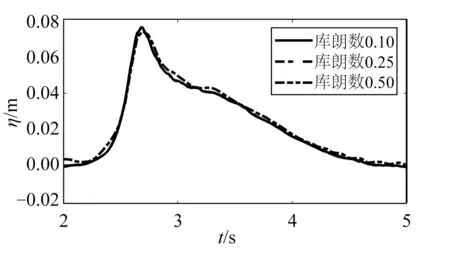
图5 不同库朗数下g22处波高历时曲线Fig.5 Wave elevations at g22 under different Courant numbers

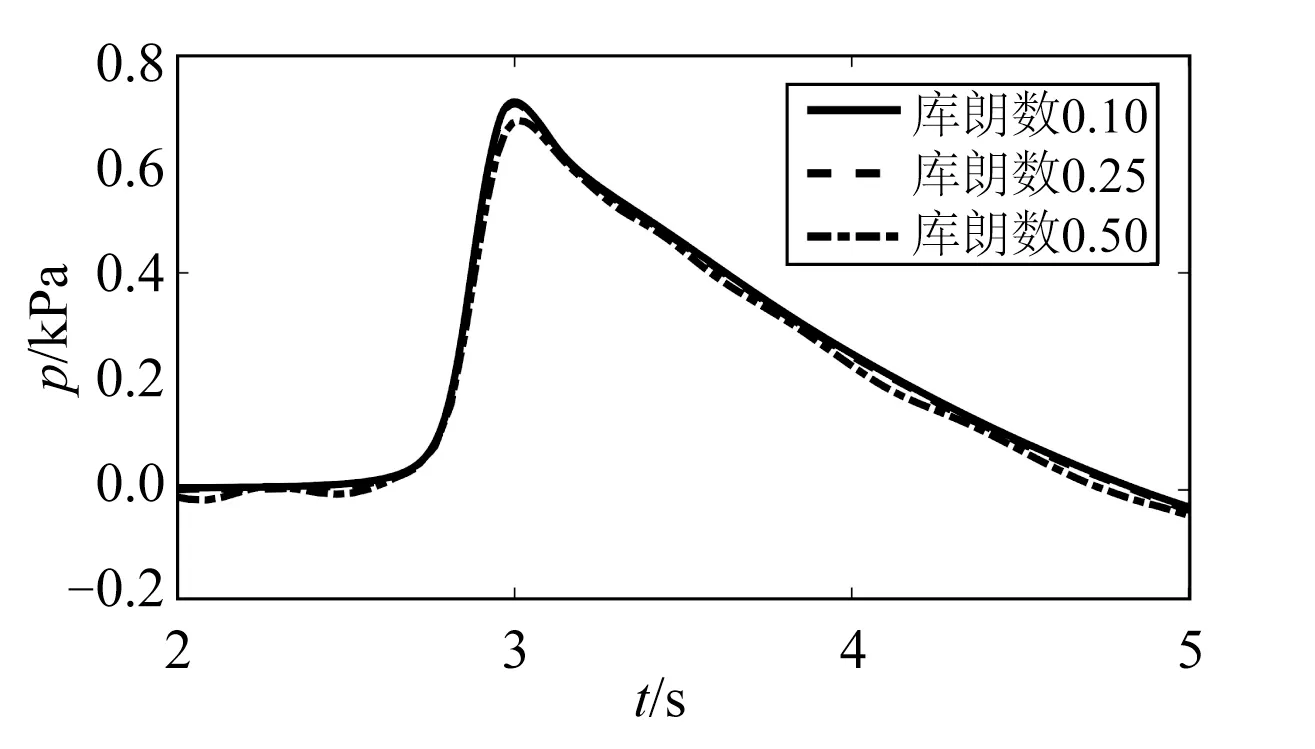
图6 不同库朗数下p7动压强历时曲线Fig.6 Dynamic pressures at p7 of the seawall under different Courant numbers

2.3 数值模拟与试验结果对比分析

图7 所示为波高历时曲线数值模拟结果与试验结果对比，波高峰值的平均相对误差为3%；图8 所示为孤立波对海堤的动压强数值模拟结果与试验结果对比，动压强峰值的平均相对误差为4.9%；图9 所示为孤立波对海堤两侧的动压力数值模拟结果与试验结果对比，动压力峰值的平均相对误差为5.1%。总的来说，OpenFOAM 模拟结果与试验结果吻合良好。但是对于后坡冲击压强和压力，OpenFOAM 峰值略小于试验峰值。这是由于数值模拟基于二维不可压缩模型，难以准确模拟该过程中的水气掺混现象，导致计算的压强和压力与试验结果具有偏差。总体来说，OpenFOAM能够较为准确模拟孤立波越浪。

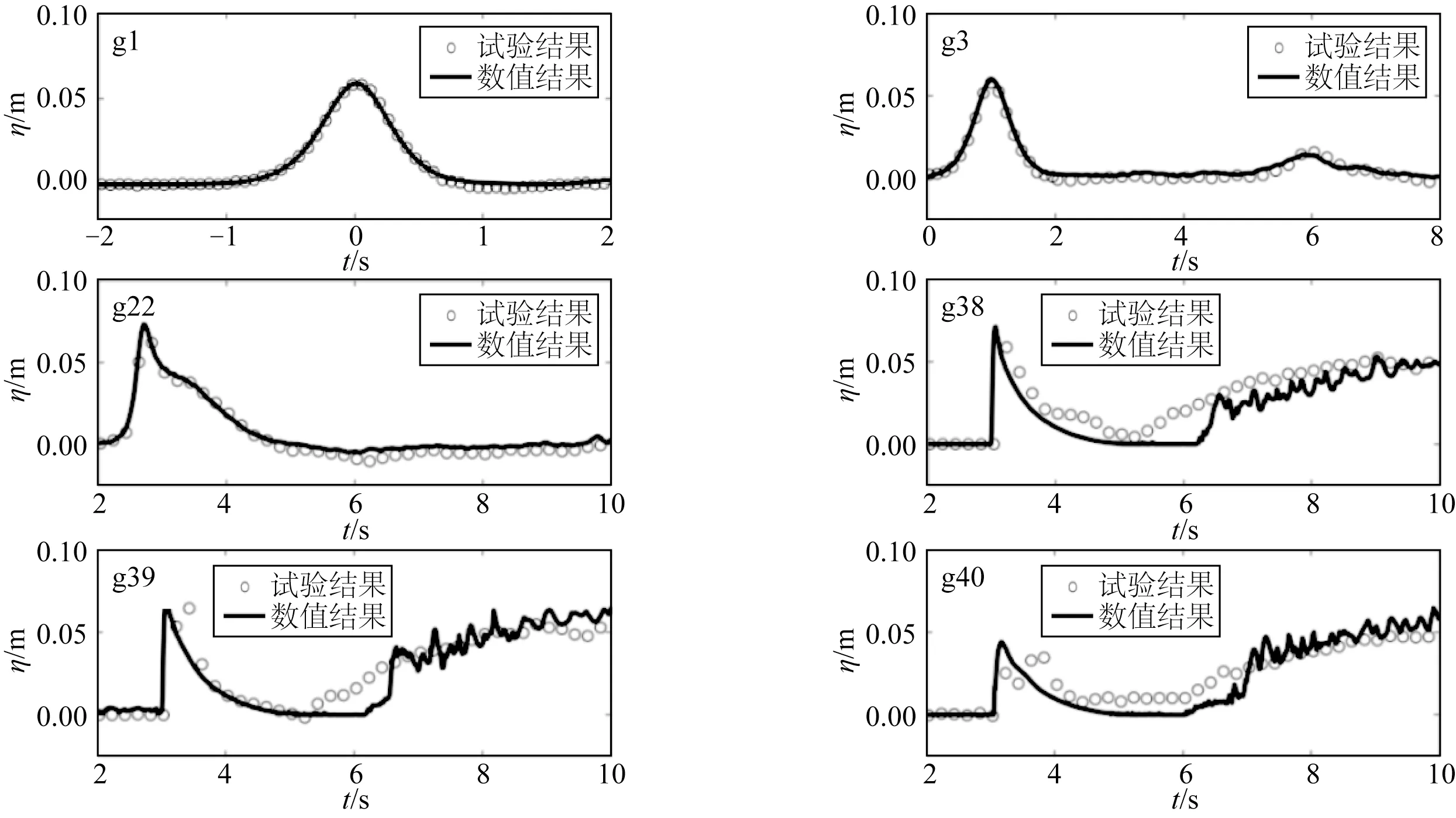
图7 H0=0.256 m, h0=0.058 9 m下典型位置的波高历时曲线Fig.7 Wave elevations at typical positions of H0=0.256 m, h0=0.058 9 m

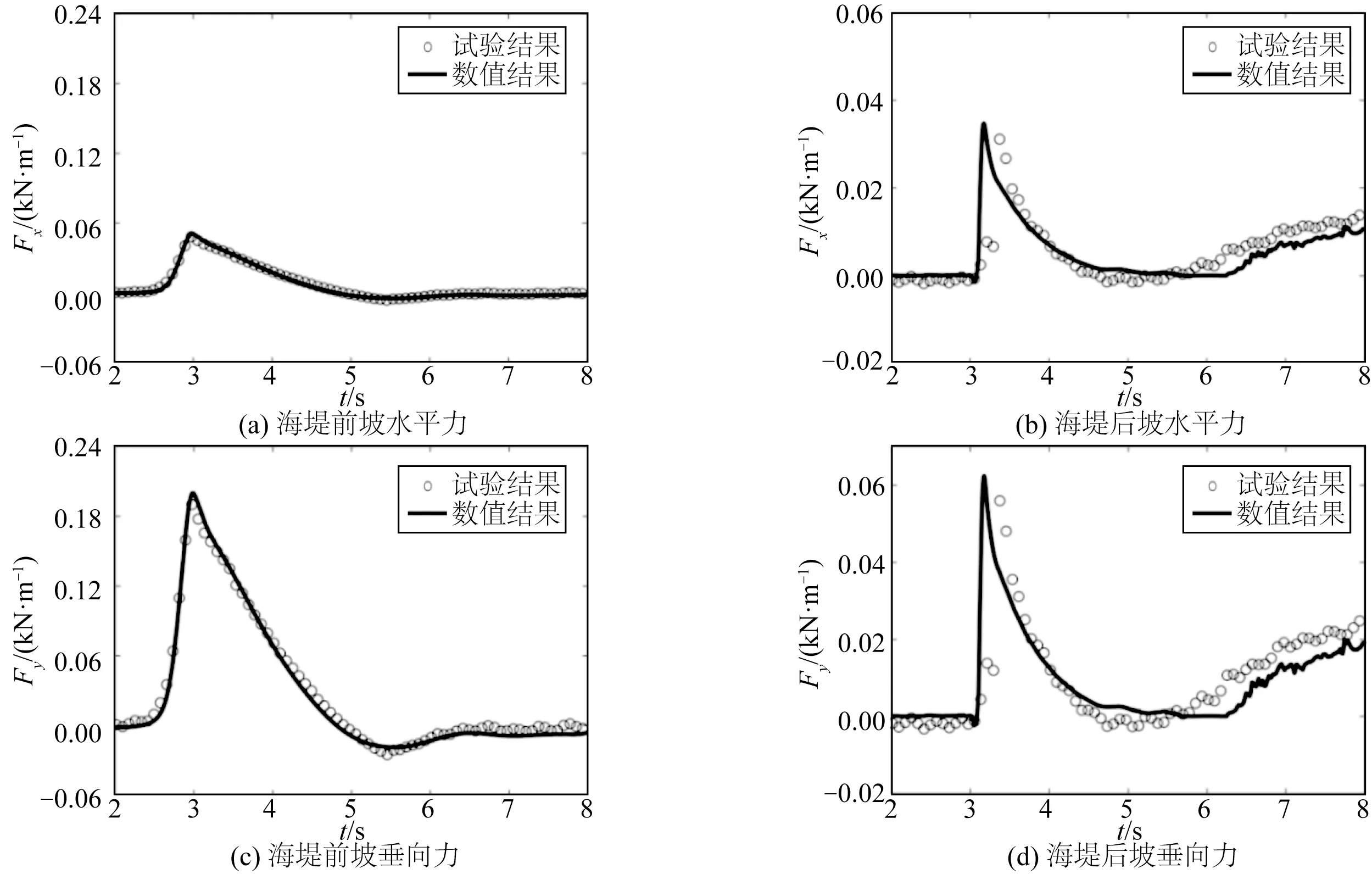
图9 H0=0.256 m, h0=0.058 9 m下海堤两侧动压力Fig.9 Dynamic forces on the seawall of H0=0.256 m, h0=0.058 9 m

3 浙江省某海堤孤立波越浪的数值模型设置

以我国浙江省沿海普遍采用的斜坡堤海堤断面型式为原型，对浙江省海岸的越浪特性开展研究。综合考虑计算效率和Froude相似准则，采用缩尺比为λ=16的海堤进行数值模拟。图10为数值波浪水槽示意，在距离造波边界10 m处有一坡比为1∶20的斜坡，斜坡长度为5 m；斜坡后方连接海堤，海堤前坡坡比为1∶3，长度为0.6 m；海堤堤顶高度为0.45 m，宽度为0.325 m；海堤后坡坡比为1∶2，长度为0.4 m；海堤后方为平底地形，高度为0.25 m。

图10 中国浙江省典型海堤数值波浪水槽示意Fig.10 Schematic diagram of the numerical wave flume with the typical seawall of Zhejiang Province, China

浙江省近岸区域的水深为6.4～7.2 m、有效波高为0.96～1.92 m。根据缩尺比，研究0.40、0.42、0.44 和0.45 m 四组水深以及0.06～0.12 m 七组波高，共28组工况，如表4所示，其中qmax为最大越浪率，q*为无量纲单宽越浪量。

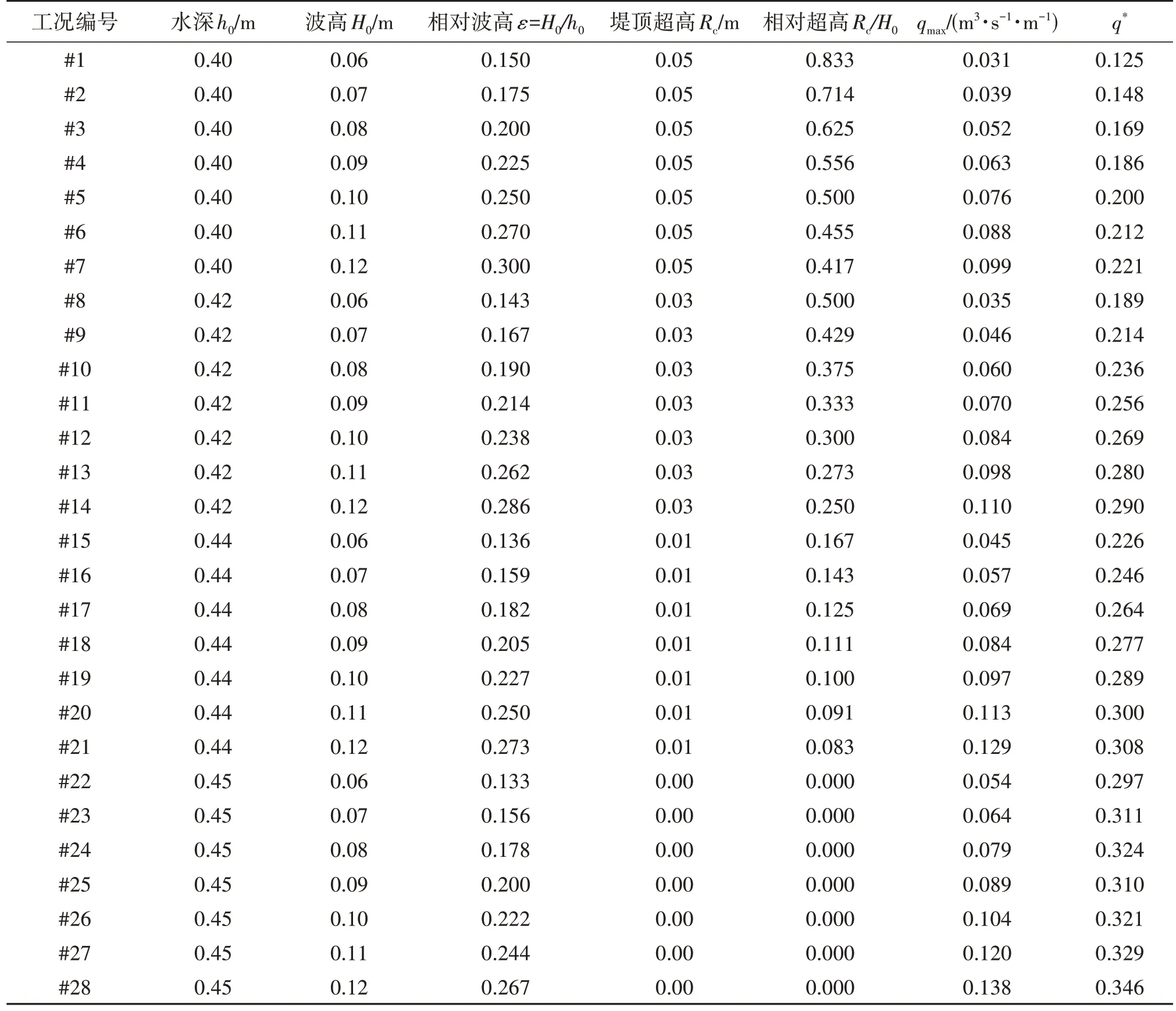
表4 28组工况下的孤立波参数及最大越浪率和无量纲单宽越浪量Tab.4 Solitary wave parameters, maximum overtopping rate and dimensionless unit width overtopping volume of 28 cases studied

海堤的堤顶超高Rc指堤顶到静止水面的距离，可通过改变水深实现不同的堤顶超高，堤顶超高与波高的比值为海堤相对超高Rc/H0。

4 结果与讨论

4.1 越浪形态

图11所示为h0=0.40 m（Rc=0.05 m）、H0=0.12 m工况，孤立波经过海堤的代表性时刻波面形态。孤立波峰在8.84 s时达到海堤堤趾，由于海堤前坡水深急剧变浅，波峰前侧波高增大（图11（a））；波浪沿着前坡爬升至海堤堤顶，未发生破碎（图11（b）），并直接越过海堤堤顶（图11（c）），而后沿着海堤后坡流下（图11（d）），并冲击海堤后坡（图11（e））以及海堤后方的建筑物和设施（图11（f））。

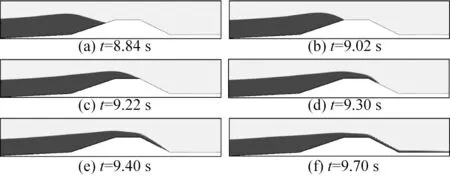
图11 工况7中代表性时刻的孤立波爬升和越浪形态Fig.11 Profiles of solitary wave run-up and overtopping at typical time instants in Case 7

图12 所示为h0=0.45 m（与堤顶高程相同）、H0=0.12 m 工况，孤立波经过海堤的代表性时刻波面形态变化。孤立波峰在8.68 s时到达海堤堤趾，由于水深变浅，波高增大，在海堤前坡未发生破碎（图12（a））。越浪水体到达海堤堤顶时，直接越过海堤堤顶（图12（b））；随着越浪水体的进一步传播，波浪越过海堤顶部沿着后坡流下（图12（c），图12（d）），直接冲击海堤后坡（图12（e）），对海堤后的建筑物和设施造成严重破坏，并引发内陆洪水（图12（f））。相较于h0=0.40 m，当水深与堤顶高程相同时，波浪到达时间提前，越过堤顶所需时间减少，越过的水体增加，对海堤后方造成的危害加大。

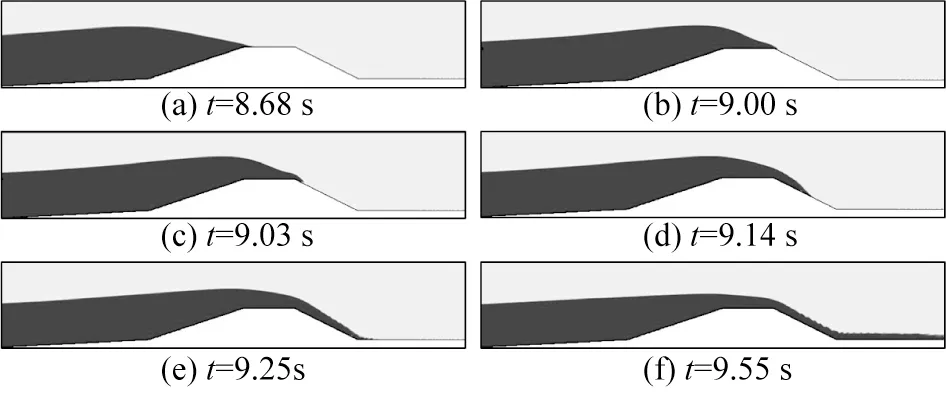
图12 工况28中代表性时刻的孤立波爬升和越浪形态Fig.12 Profiles of solitary wave run-up and overtopping at typical time instants in Case 28

4.2 越浪量

在数值模拟中，统计孤立波经过海堤堤顶与后坡交界处（x=15.925 m）在不同时间下的单宽越浪率（m3·s−1·m−1），对时间积分得到单宽越浪量q（m3/m）。采用Baldock 等［5］的公式形式，引入孤立波在静水面以上的单宽水体体积q0，最终计算得出单宽无量纲越浪量q*，对式（16）积分可得q0为：

式中：h0为水深，H0为孤立波波高。

单宽无量纲越浪量q*的计算式为：

采用式（18），计算得到文中所有工况下的无量纲单宽越浪量q*。表4所示为各工况下的最大越浪量qmax和无量纲单宽越浪量q*。

图13 所示为最大越浪量与水深、波高的关系。由图13 可知，随着水深和波高的增大，最大越浪量显著增大。当水深与海堤堤顶高度接近或齐平时，即使很小的波也会产生较大越浪量，对海堤上及堤后的人员和建筑物造成严重威胁。

图13 不同水深和波高下的最大越浪量Fig.13 The maximum overtopping volume at various water depths and wave heights

前人关于越浪量经验公式的研究认为，影响越浪量的因素主要分为两类：第一类为波浪要素，包括水深、入射波高、波周期、波陡等；第二类为海堤几何尺寸，包括海堤堤顶高度、堤顶宽度等。

文中模拟的海堤表面光滑且几何尺寸不变，对越浪量进行无量纲化处理，得到越浪量与各影响因素之间的函数关系式为：

根据π 定理，由量纲分析得到如下的无因次函数关系：

通过对前人的研究成果进行对比分析，同时考虑到文中模拟为堤顶超高很小或为0情况，提出的孤立波越浪计算公式采用张金牛［6］提出的结构形式为：

式中：a，b，c均为经验参数。采用多元线性回归方法对数值模拟所得的越浪量数据进行拟合，得到如下预测公式：

图14为孤立波作用下海堤无量纲越浪量的数值模拟结果与公式预测结果的比较，由图可知二者结果吻合较好，拟合的均方根误差仅为0.015 3，表明公式预测结果与数值模拟结果具有较高的一致性。Baldock等［5］提出采用爬高计算越浪量，在计算h=0.40 m、0.42 m 时越浪量为负值，与实际不符，式（22）的计算公式更接近低顶情况下的越浪量。

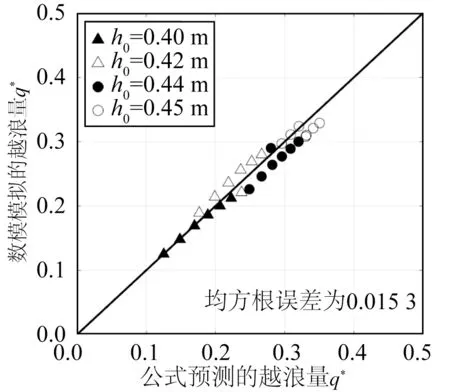
图14 无量纲单宽越浪量模拟结果与公式预测结果对比Fig.14 Comparison between the simulated dimensionless unit width overtopping volume and the predicted results by the proposed formula

4.3 越浪引起的波浪力

孤立波拍打在海堤上时，产生相当大的波浪力，对海堤的结构安全产生威胁。图15为水深0.40 m、不同波高下，海堤前坡和后坡所受的单宽水平和垂向波浪力。结果表明，对于前坡，其所受的垂向力为水平力的3 倍，这是由前坡的坡度决定。随着波高的增加，前坡受到的波浪力显著增大，其中水平力从波高0.06 m 时的0.165 kN/m 增加到波高0.12 m 时的0.243 kN/m，垂向力从波高0.06 m 时的0.495 kN/m 增加到波高0.12 m时的0.728 kN/m，增长了47%。由于海堤前坡的坡度较缓，前坡所受水平力较小，具有较好的抗倾覆能力。此外，这种缓坡海堤对孤立波的阻力也较小，引起的波浪反射较少。因此，波浪会以较大的速度在前坡爬升并越过堤顶，对海堤后方的建筑物和设施产生较大的波浪力，造成更大的破坏。对于后坡，由于孤立波经过海堤时，其所受的波浪力比前坡小，后坡所受的垂向力为水平力的2 倍。随着波高的增加，后坡受到的波浪力也增大，增长幅度为177%，远大于前坡，后坡结构更易受到波浪力的影响。

图15 水深0.40 m，不同波高下海堤两侧波浪力Fig.15 At water depth of 0.40 m, wave forces on both sides of the seawall under different wave heights

图16 为不同水深和波高下的最大波浪力。由图16 可知，在相同波高下，随着水深的增加，海堤前坡所受的波浪力无显著差异，海堤后坡所受的波浪力随水深变化明显。这是由于海堤后坡所受波浪力由越过堤顶的波浪产生，水深的增大导致越过堤顶的波浪增加，对后坡产生的波浪力也越大。

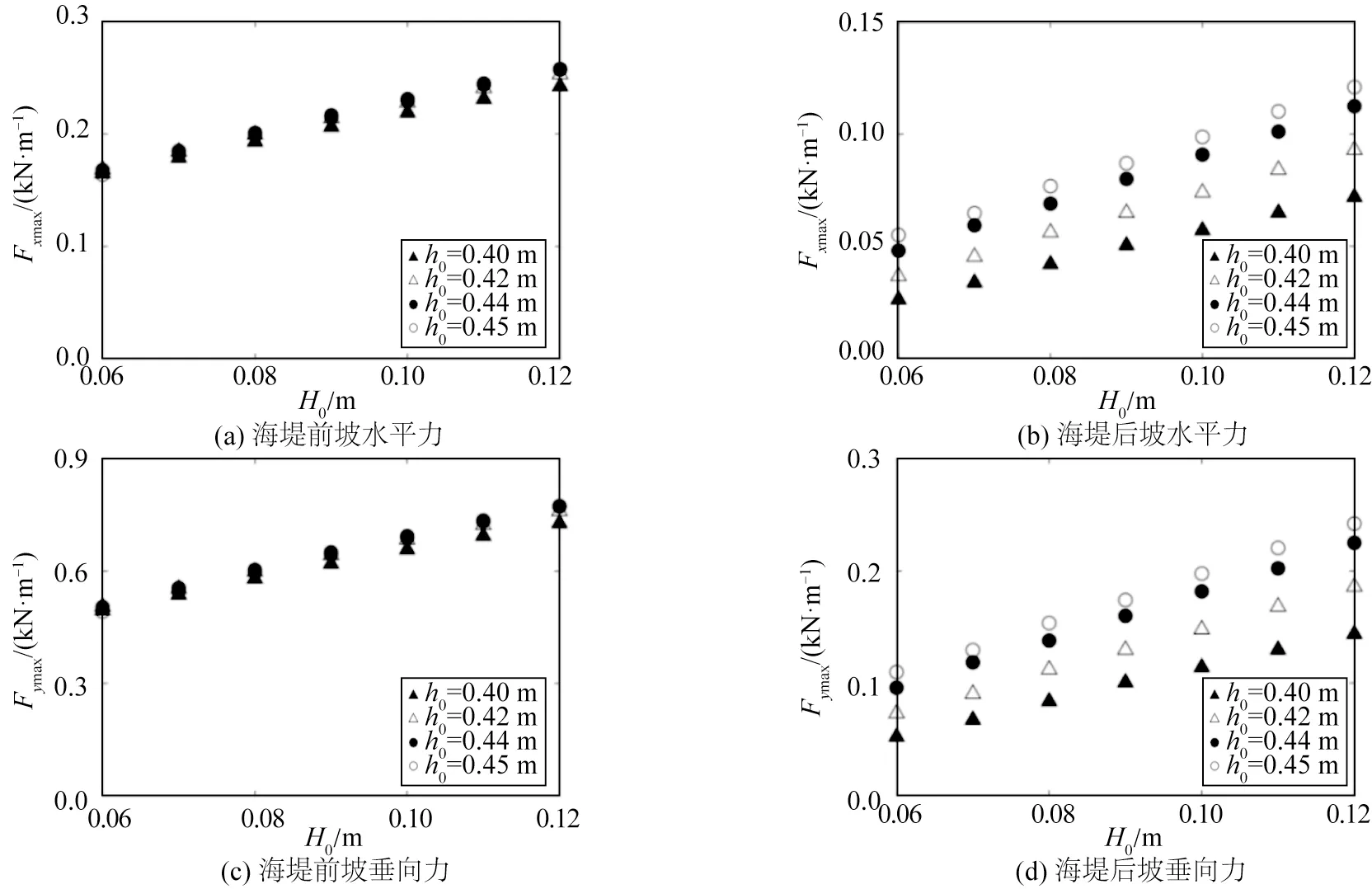
图16 不同水深、波高下的最大波浪力Fig.16 The maximum wave forces on the seawall at different water depths and wave heights

4.4 防浪墙高度对越浪的影响

由于海平面上升，浙江沿海海堤堤顶高度不满足海堤建设规范要求的可容忍限度越浪量。为了应对海平面上升以及极端海况下的越浪问题，一种方式是在海堤顶部建造防浪墙（通常是在局部海岸建造），以增加堤顶超高，在增加少量成本的情况下提高安全性。因此，文中提出在海堤堤顶向海一侧（x= 15.6 m）设置一个防浪墙（如图17所示），研究防浪墙宽度dw=0.01 m、高度hw分别为0.10、0.12、0.14、0.16、0.18、0.20 m在最不利工况28下的越浪特性。

图17 带防浪墙的海堤断面示意Fig.17 Schematic diagram of the seawall with a crown wall

图18为孤立波经过防浪墙高度为0.20 m 的波面形态演变。当孤立波爬升至海堤堤顶时，由于防浪墙的存在，无法直接越过堤顶，而是冲击墙体并沿着墙面爬升（图18（a））；当波浪达到防浪墙顶部时（图18（b）），水体继续往上升，超过防浪墙顶部（图18（c））；当达到极限高度时，水体坍塌，少量水体回落至前坡，大部分水体从防浪墙后侧落下（图18（e））；越过防浪墙的水体在重力作用下产生堰流冲击海堤堤顶（图18（f））；堰流冲向堤顶破碎，分成两股流（图18（g）），一股沿着后坡流下，另一股流向防浪墙后侧墙面（图18（h））。

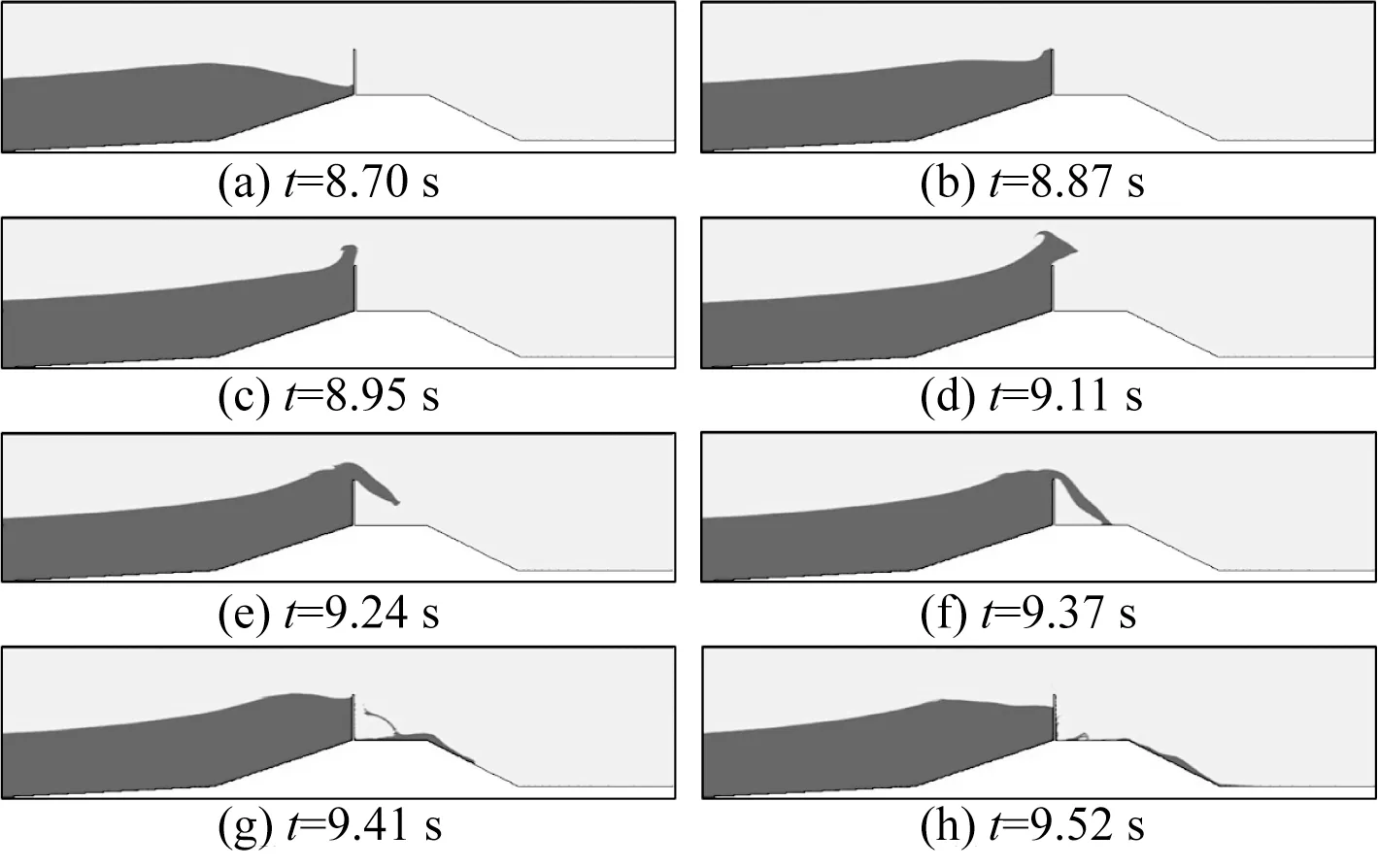
图18 防浪墙高度0.20 m的波面形态演变Fig.18 Wave profiles with crown wall height of 0.20 m

波浪越过墙体的越浪量及其对防浪墙的波浪力与防浪墙高度有关。使用国内外学者普遍认可的方式［15-17］对防浪墙高度以及最大波浪力进行无量纲化，即防浪墙高度Hw除以波高H0得到无量纲防浪墙高度，单宽最大波浪力除以ρgH0dwhw得到无量纲化单宽最大波浪力F*。图19为不同无量纲防浪墙高度下的单宽越浪量和最大单宽越浪波浪力，其中防浪墙高度Hw*=0 表示海堤上方无防浪墙的情况。相较于无防浪墙的海堤，防浪墙的存在能够有效减少孤立波的越浪，极大减少越浪对海堤后方建筑物及人员的破坏作用。具体来说，当防浪墙高度为0.10～0.14 m 时越浪量线性减小，进一步增加防浪墙高度越浪量减小趋势减缓。然而，防浪墙所受的波浪力随其高度呈现先减小后增大而后又减小的趋势：Hw*为0.83时受到最大波浪力q*=0.133，Hw*=1.00 受到最小波浪力q*=0.115；进一步增加Hw*受到的波浪力增大，在Hw*=1.33 达到最大值q*=0.124；而后波浪力随Hw*减小。综合考虑防浪墙减少越浪效果以及自身所受波浪力，针对文中采用的海堤截面和波浪条件，建议为1.00。

5 结 语

采用OpenFOAM 建立数值水槽，模拟研究孤立波的低顶海堤越浪特征以及越浪在海堤两侧产生的波浪力，同时探究海堤顶部防浪墙高度对越浪的影响。

所有工况下的波浪均未在海堤前坡发生破碎，孤立波越过堤顶，沿海堤后坡流下，直接冲击堤后建筑物和设施。堤顶超高减小导致更为剧烈的越浪，这意味着在全球海平面上升的背景下，沿海城市面临着更大的海堤越浪和海水倒灌风险。针对低顶海堤孤立波越浪量经验公式的不足，文中提出适用于堤顶超高小或为0的孤立波越浪量经验公式，公式预测结果较为准确。

在海堤顶部设置防浪墙增加海堤堤顶超高，可有效减少越浪，但防浪墙所受的波浪力也增大。综合考虑防浪墙减少越浪效果以及自身所受波浪力，针对文中采用的海堤截面和波浪条件，建议无量纲防浪墙高度为1.00。