台风过程下复式海堤越浪量计算方法研究
2019-12-03陈韬霄郑国诞胡金春董伟良
陈韬霄,郑国诞,邵 杰,胡金春,陈 刚,董伟良
(1.浙江省水利河口研究院,浙江 杭州 310020;2.浙江省河口海岸重点实验室,浙江 杭州 310020)
1 问题的提出
台风作用时,随着堤前水位抬高和风浪的增大,波浪作用于海堤迎潮面,或沿坡面上爬,或发生破碎击打坡面,波浪沿着海堤迎潮面上爬超过堤顶则会出现明显的越浪现象,水体飞溅于堤顶和内坡面。越浪量的大小与堤前波浪要素、堤顶出水高度、海堤的几何外形、护面的糙渗特性等有关。若台风登陆时遭遇天文高潮,海堤越浪量将迅速增大,对海堤安全造成威胁,因此研究计算台风过程下复式海堤越浪量的方法,结合台风浪与风暴潮实时预报情况,为台汛期间的高效避灾提供科学依据。
目前最常见的海堤结构形式为斜坡式海堤、直立式海堤以及混合式海堤,遭受台风较严重的浙江省温台地区新建的堤防均以复式斜坡式海堤(简称“复式海堤”)为主。从20世纪初开始,国内外学者对海堤越浪量问题进行了大量的研究工作。Owen(1980 — 1991年)对单坡及复坡海堤越浪量进行了系统研究[2-4];周家宝(1990年)等进行了试验研究,提出的海堤平均越浪量的计算公式被JTJ 213 —1998《海港水文规范》所采用[5-7];陈国平(2010年)开展不规则波作用下的海堤越浪量试验研究,分析越浪量的各影响因素,并提出不规则波越浪量的计算公式[8]。邵杰(2018年)在试验的基础上,引入海堤越浪量折减系数的概念,拟合带挡浪墙的复式海堤越浪量计算公式[9]。以下为国内目前常用的一些越浪量计算公式:
(1)《港口与航道水文规范》[7]中给出斜坡堤有无防浪墙的越浪量计算公式:
堤防有防浪墙时:

式中:Q为单位时间单位堤宽的越浪量(m3/(m · s));Hc胸墙墙顶在静水面以上的高度(m);H1/3为有效波波高(m);b1为胸墙前肩宽(m);B为经验系数;KA为护面结构影响系数;TP为谱峰周期;m为斜坡坡度系数。
(2)陈国平(2010年)[8]开展不规则波作用下的海堤越浪量试验研究,分析越浪量的各影响因素,并通过置信度95%拟合提出不规则波越浪量的计算公式:
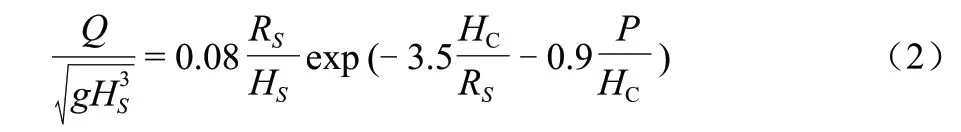
式中:Q为平均越浪量(m3/(m · s));RS为累积率13%的波浪爬高(m);HC为防浪墙顶超高(m),当无防浪墙时,HC=RC;P为防浪墙高度(m),对于堤顶未设置防浪墙斜坡断面,P= 0。
(3)邵杰(2018年)[9]首先开展单斜坡堤越浪量试验,拟合出单斜坡海堤越浪量计算公式,在此基础上引入海堤越浪量折减系数的概念,最终得到带挡浪墙的复式海堤越浪量计算公式:

式中:q为平均越浪量(m3/(m · s));dh为平台上水深(m);Hs为有效波高(m);B为平台宽度(m);m为海堤坡度;HC为防浪墙堤超高(m)。
工程越浪量计算应用以上国内较常见的越浪量计算方法中,式(2)与式(3)可以通过波浪爬高计算复式斜坡堤的越浪量,其它多为针对单一斜坡式,且在台风过程中海堤较大越浪量计算的适用性还未可知。很多重要工程考虑到经验公式计算的缺陷,需进行物理模型试验得到越浪量。本文拟通过台风浪过程中海堤越浪量的模型试验成果,探讨现有复式海堤越浪量计算公式的适用情况,在试验成果的基础上,得到一种计算台风过程中复式海堤越浪量的方法。
2 断面模型试验
2.1 试验断面
选取复式海堤开展越浪量试验。复式海堤在上海、浙江、福建等省市得到广泛应用,具有良好的代表性,概化断面见图1。迎水面为1:3的复式斜坡,高潮位附近设消浪平台,堤顶设1.00 m高挡浪墙,内坡坡度1:2,防浪墙顶高程参考浙江平阳沿海,设为8.40 m。

图1 试验概化断面图
2.2 水文条件
设计台风路径取浙闽交界处登陆的0608#“桑美”台风实际路径,登陆气压915 hPa,利用风暴潮和台风浪数模计算得到堤前潮位、波浪过程。试验采用梯级逼近近似潮位与波浪过程,试验组次见表1。不规则波模拟采用常用的JONSWAP波谱作为目标谱。
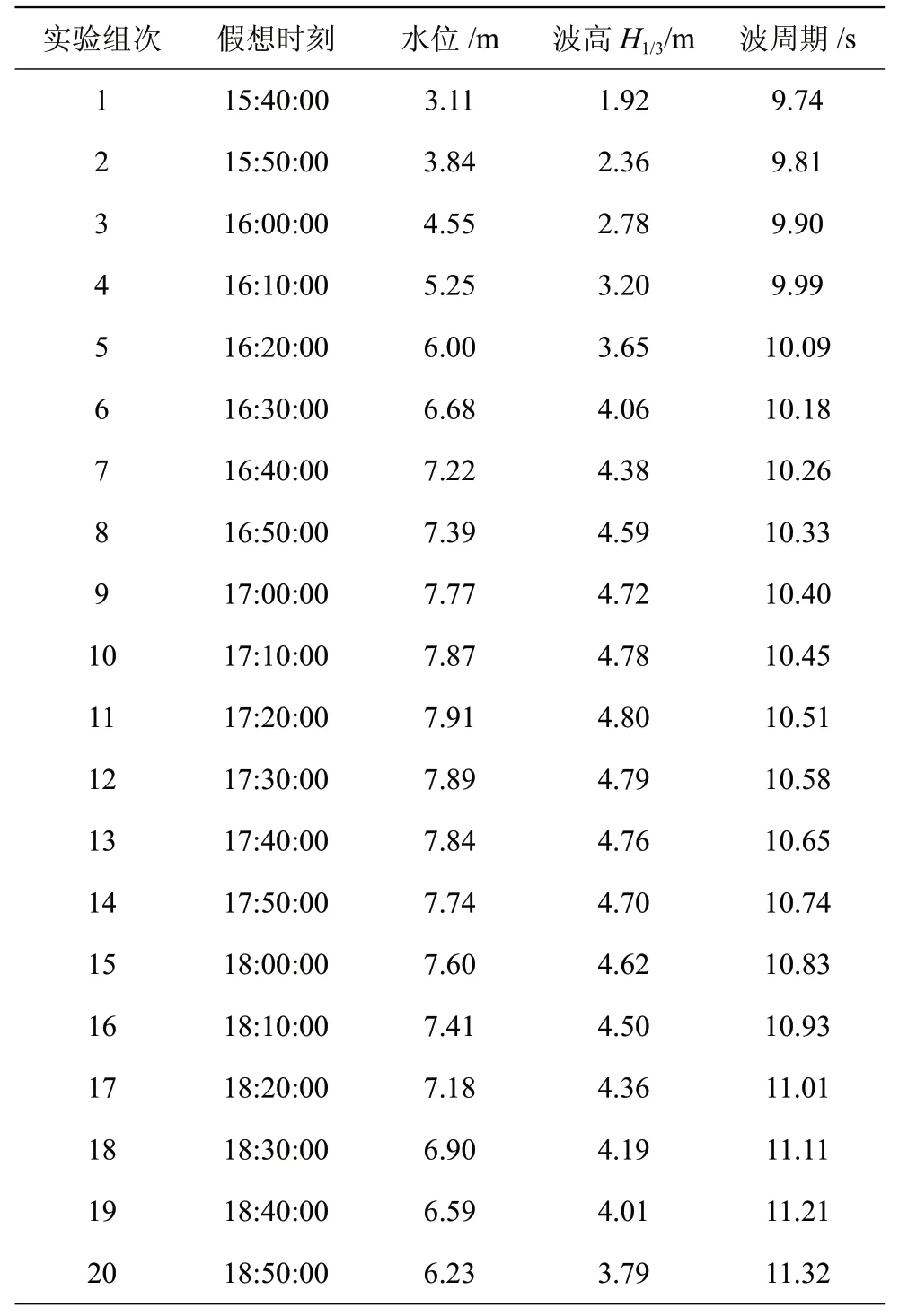
表1 试验水文条件表
2.3 海堤越浪量测定
根据风暴潮位过程 — 波浪组合对海堤断面开展台风浪越浪量试验,并在较高潮位时进行适当加密,越浪量数值均为假设断面防浪墙和堤顶不发生破坏时的测量值,对每个工况组合试验均重复测量3次,以减小偶然因素的影响,测得海堤越浪量结果见图2 ~ 3。
从图2 ~ 3中可以看出,与潮浪过程相对应,越浪量也经历了从小到大的过程,低潮、中潮位时刻,海堤断面几乎没有越浪现象,随着潮位的增加(潮位达4.55 m时),海堤断面开始出现明显越浪量,此后时刻的海堤断面越浪量迅速增加,最高潮位前1.0 h(假定时刻16:20),海堤断面越浪量为0.138 m3/(m · s),最高潮位前0.5 h,断面越浪量达到0.837 m3/(m · s),此时对应潮位为7.39 m,尚低于挡浪墙顶高程约1.00 m。此外最高潮位前1.0 h,每隔5 min,后一时刻的越浪量即可达到前一时刻的1.2 ~ 2.0倍。试验表明,台风浪过程下随着潮位的增加,海堤越浪量将迅速增大,威胁海堤安全。
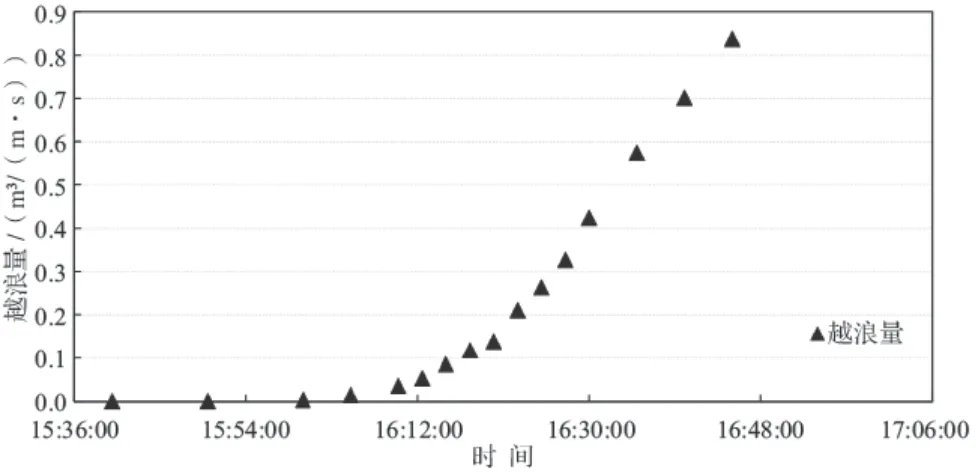
图2 越浪量试验结果图
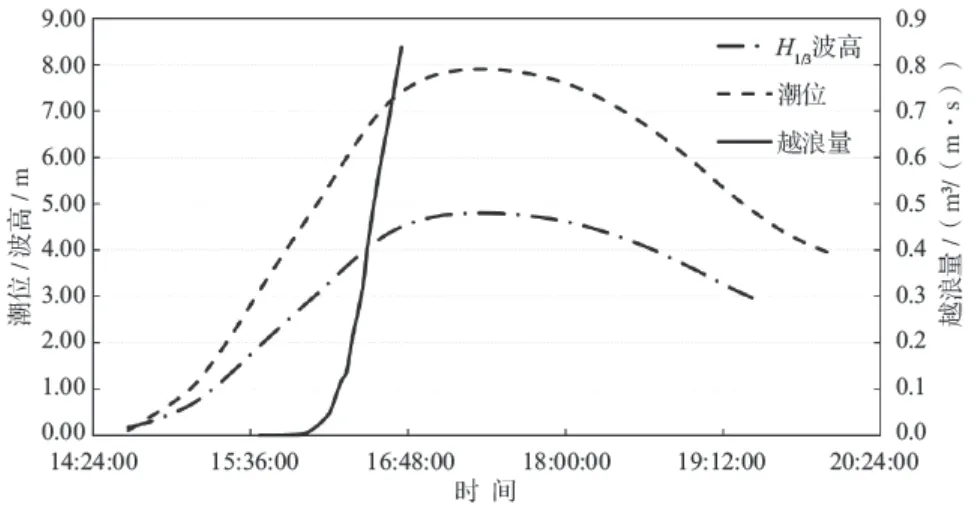
图3 越浪量、潮位、波高相互关系图
3 越浪量公式
3.1 公式计算值与试验值比较
通过现行常用越浪量公式计算值与试验值进行比较(见图4),可见前文2种越浪量计算方法对于小越浪量适用情况都较好,但是对于大越浪量的计算适用性并不理想。
在越浪量为0.050 ~ 0.200 m3/(m · s),式(3)计算值平均差为20.1%,式(2)计算值平均差为47.1%,计算精度相对较高;随着水位抬高,海堤越浪量逐渐增大,越浪量在0.200 ~ 0.830 m3/(m · s)范围内,式(2)计算值平均差为48.9%,式(3)计算值平均差为56.5%,计算结果与试验值相差均较大。由此可见,当海堤越浪量超过0.200 m3/(m · s)时,式(2)与式(3)的适用性均相对较差。
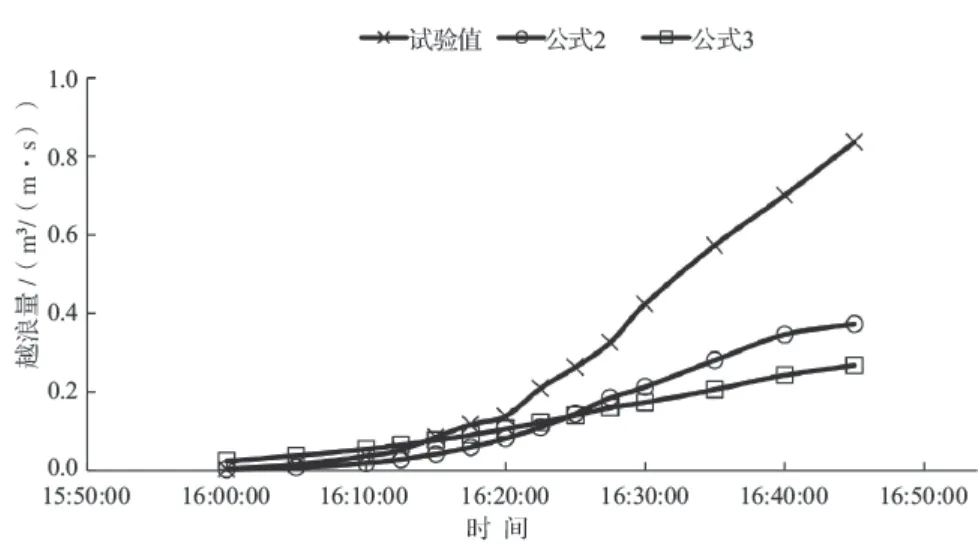
图4 海堤溃堤越浪量试验值与经验公式计算结果对比图
3.2 越浪量公式推求
考虑到各越浪量公式的计算结果,在不同越浪量区间的表现形式不一样,式(3)在小越浪量的计算中表现误差较小,但在大越浪量的计算中适用性相对较差。本次研究在式(3)基础上,拟合得到一种计算台风过程中复式海堤越浪量的公式。
平台上相对水深dh / Hs往往与越浪量或波浪爬高的折减系数较为密切,将式(3)中Q试验/ Q公式与相对水深dh / Hs之间做相关性分析,相关系数R2可达0.98,越浪量试验值与计算值之比与相对水深的变化存在着非常好的相关性(见图5)。
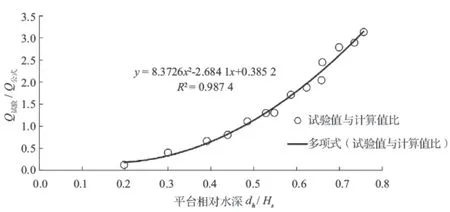
图5 越浪量公式计算与试验值之比与相对水深关系图
因此,以试验数据分析为基础,通过相对水深这一因子对计算越浪量公式进行推求,拟合系数KT,使其计算结果更加接近试验值,拟合公式结果如下:
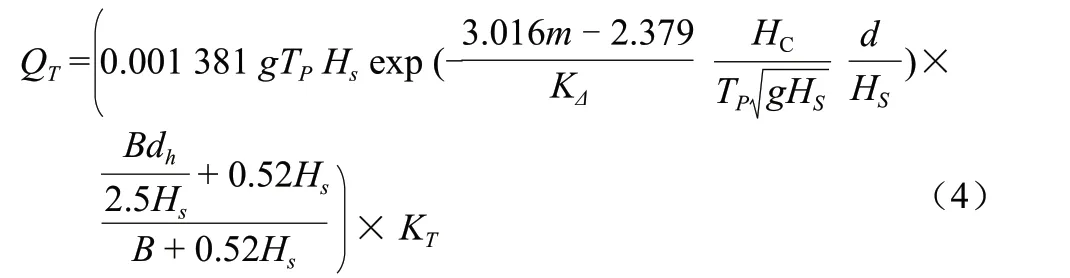
将拟合后的公式越浪量计算值与试验值进行对比,对比结果见图5 ~ 6。经拟合后的越浪量公式计算值与试验值明显较之前接近,越浪量在0.015 ~ 0.837 m3/(m · s)区间内公式计算值与实验值的总体平均误差绝对值为5.7%,其中当实测越浪量处于0.003 ~ 0.036 m3/(m · s)区间内,平均误差约为22.6%;当实测越浪量处于0.052 ~ 0.209 m3/(m · s)区间时,平均误差约为3.7%;在越浪量高于0.209 m3/(m · s)时,平均误差约为5.2%。
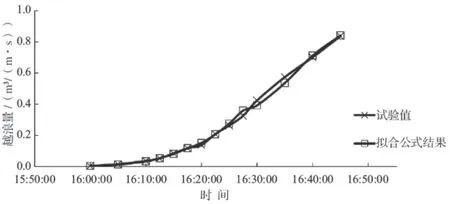
图5 拟合公式计算值与试验值比较图

图6 拟合公式与试验值误差随越浪量实测值变化图
在小越浪量的情况下,拟合公式计算值仍存在22.6%的误差,随着越浪量的增加,拟合公式计算值误差减小,海堤大越浪量的情况下,误差基本在5.7%左右。因此,该公式可用于极端天气条件下越浪量的估算,具有一定的工程实用价值,为台风过程中复式海堤越浪量的评估具有重要意义。
4 结 论
(1)试验表明,台风浪模拟过程中,越浪量经历了从小到大的过程,随着潮位的增加,海堤断面开始出现明显越浪量,最高潮位前1 h,每隔5 min,后一时刻的越浪量即可达到前一时刻的1.2 ~ 2.0倍。
(2)将现行常用越浪量公式计算结果与试验成果进行对比,对于小越浪量情况适用情况都很好,但是对于大越浪量的适用性相对较差。
(3)拟合公式计算结果与试验成果进行对比,随着越浪量的增加,公式计算值误差减小,海堤大越浪量的情况下,误差基本在5.7%左右,可用于极端天气条件下的越浪量估算,对台风过程中复式海堤越浪量的评估具有重要意义。
