潜航器微气泡减阻数值模拟方法研究

詹杰民，陆尚平，李熠华，李雨田，胡文清

（中山大学 应用力学与工程系，广东 广州 510275）

在走向深海的总体战略思想指导下，水面舰船及潜航器（如水下探测器、鱼雷和潜艇等）的发展趋势是具有更高航速和更远航程。为了满足上述需求，设法减小航行阻力无疑是最为直接有效的方式。舰艇在航行过程中，受到的阻力一般由兴波阻力、压差阻力和黏性阻力3 个部分组成，通常占主导地位的是黏性阻力［1］。其中水面舰船受到的黏性阻力通常占总阻力的50%左右，而潜航器的黏性阻力占比最高可达70%［2］。因此如何减小航行器受到的黏性阻力便成为水面、水下减阻技术领域的重点研究方向，其中微气泡喷射减阻日益成为高速航行器黏性减阻的常用方法。

Latorre等［3］采用微气泡垂直喷射方法对带有非湿润涂层的高速模型进行了模型试验。结果表明涂层的减阻率为4%～6%，带有涂层的微气泡总减阻率为4%～11%。Wu等［4］采用试验观察和测量技术，讨论了液体湍流边界层与群聚微气泡之间的相互作用影响，并比较了两种孔隙率下的减阻效率。Zhao 等［5］采用OpenFoam 开源软件研究了轴对称结构的两相微气泡流动，结果表明边界层内的气流速度和空气体积分数对微气泡减阻起到重要作用。Mohanarangam 等［6］采用欧拉—欧拉双流体模型研究了微气泡注入湍流边界层的减阻现象，对减阻的复杂机制进行了仔细剖析，并研究了由随机碰撞和湍流冲击引起的气泡聚结和破裂的影响。Xu等［7］采用直接数值模拟方法，对平均体积分数为8%的湍流通道流进行了系列研究，结果表明即使是相对较大的气泡，也会出现初始瞬态减阻现象而相对小的球形气泡会产生持续的减阻效果。Li等［8］提出了一种制造柔性皮肤状装置的方法，用于产生和捕获微气泡以减小水下阻力，并进一步建立了多相计算流体力学模型，分析了钟形孔的减阻性能。相比于圆柱形通孔，钟形孔的减阻效果提高了34%。Zhao等［9］采用欧拉—欧拉双流体模型和流体体积（VOF）模型，研究了轴对称物体的三维空气喷射减阻。对于微气泡减阻（MBDR 或BDR）区域，空气层减阻（ALDR）区域以及两者之间的过渡区域，Zhao 等［9］建立了相应的模拟方法，结果与试验数据吻合良好。Sindagi 等［10］综述了船舶微气泡减阻的研究现状，认为阻力的降低取决于孔隙率、注入气泡的聚结和破裂、水的盐度和所用气体的类型、注入气泡的水深等，还采用Star CCM+软件，针对不同流速、不同的含气率和注入点，对微气泡减阻进行了三维数值研究。Rawat等［11］基于连续相欧拉方法和离散相拉格朗日方法，数值研究了由微气泡组成的分散相与湍流边界层流动之间的相互作用。

目前关于微气泡减阻的研究大多基于简单的平板模型或者船模，针对水下潜航器的试验和数值研究仍较为缺乏。Wu 等［12］利用k⁃ω湍流和多相流模型模拟计算了不同微气泡直径对水下回转体模型周围微气泡群分布状态和阻力的影响，认为产生的微气泡平均直径足够小时可以更好地附着于物体表面以提高气膜覆盖效果。郭峰等［13］基于Fluent软件研究了回转体潜航器微气泡减阻效率，其结果表明微气泡群可使试验模型局部黏性阻力降低80%，总阻力降低30%。黄磊等［14］设计制作了一种表面布有微孔充气阵列的回转体试验模型，并利用高速摄影仪器及动态测力系统进行了系列水洞试验。结果表明模型周围气液混合流场可分为稳定段、脉动段和回流段3个区域，而随着充气量的提高，稳定段和脉动段空隙率逐渐增加，回流段分离点渐渐向后移动，直至临界充气量饱和点。宋武超［15］基于水洞试验开展了不同流速和通气量下微气泡流形态及聚合物与微气泡减阻特性的试验研究。随后Song等［16］，宋武超等［17］在湍流水洞中开展了系列轴对称模型微气泡减阻试验研究，其试验结果表明：微气泡尺寸分布符合高斯分布；当空气充入速度较高时，均匀分散的微气泡流会凝聚成一个连续的气膜，此时的减阻效率较大；直径较小的微气泡具有更好的减阻效率。文中的回转体潜航器拖曳试验中使用喷气小孔在模型前端产生微气泡，利用试验数据和气泡流的图像来验证使用多孔介质等效喷气小孔的合理性，并使用数值模拟进一步探究微气泡减阻技术对潜航器阻力的影响规律。

1 试验研究

潜航器基于各自工作环境和目标功能的差异，在局部有着不尽相同的外形设计，但共同特点为头部近似于半球形、中部近似于圆柱体、尾部为流线型锥体，通体狭长且近乎于轴对称的结构。因此采用如图1 所示的回转体潜航器简化模型作为研究对象。该模型由3 个模块化设计的部分组成：前盖体、中艇体与后艇体，三者之间的相互对接由特殊设计的防漏气螺纹接口实现。其中前盖是一个直径80 mm 的半球壳，其上有两圈呈放射状均匀排布的用于喷射气体的小孔（共72个），孔径为 0.4 mm；中艇体外形为一个直径80 mm、长100 mm 的圆柱体；后艇体则为一个底部直径80 mm、高60 mm 的流线形锥体，3 个部分的壁厚均为6 mm。模型主体结构长度为200 mm，加上充气尾管全长为220 mm，尾管的内径为4 mm、外径为8 mm。模型内部设计有两层隔断肋板，以保证结构的整体强度，同时肋板上留有相应的通气孔洞，便于从充气尾管供入的压缩空气能顺利地流至前盖体的小孔处。另外为了在拖曳试验过程中稳定拖行试验模型并同时测量其所受到的阻力，采用如图2（a）所示的基于滑动平台的阻力测量装置，并在后艇体设计有一个方孔用于插入支撑杆，以便将试验模型与阻力测量平台进行连接、固定。

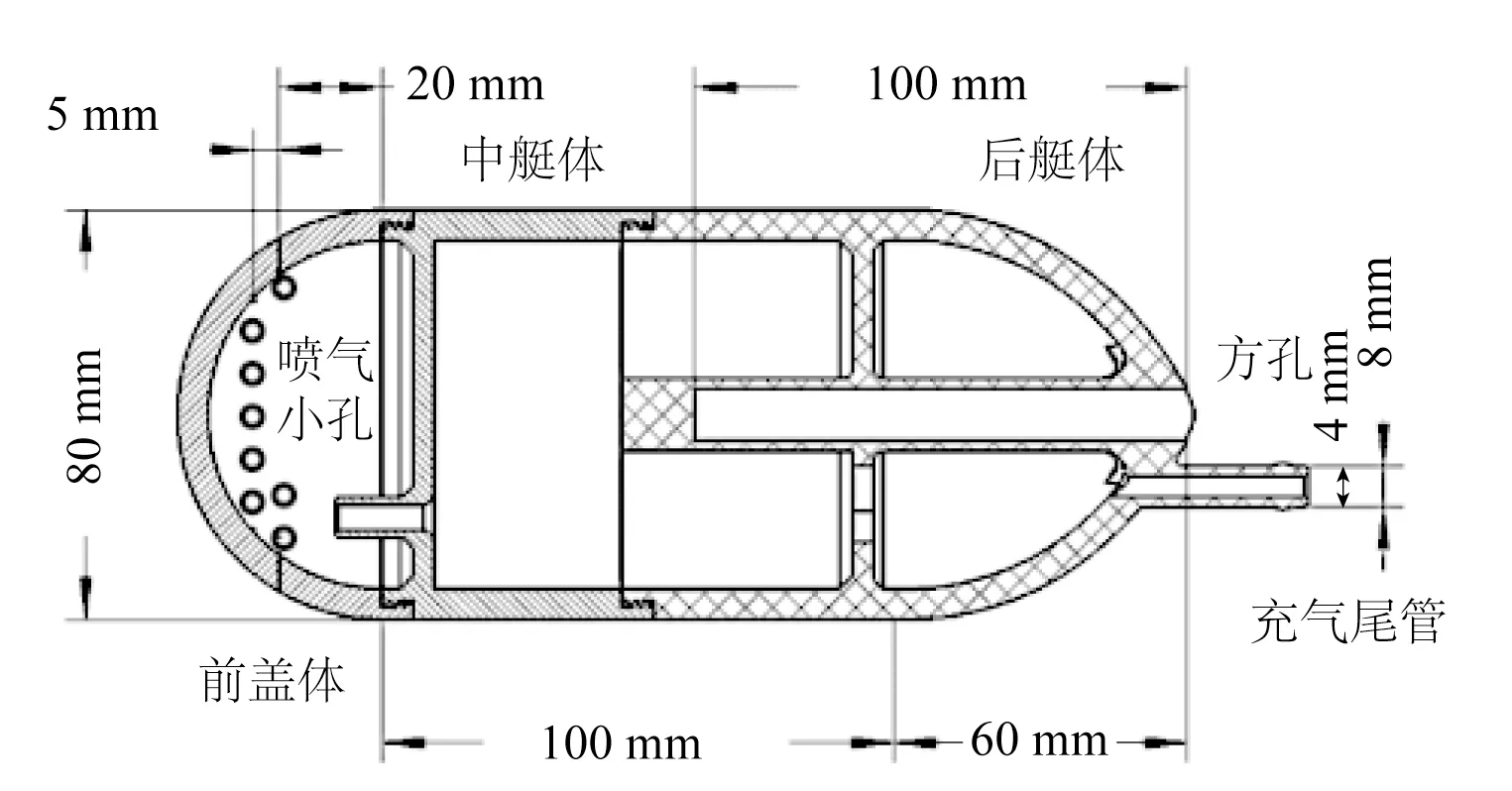
图1 试验模型示意Fig.1 Schematic diagram of the test model

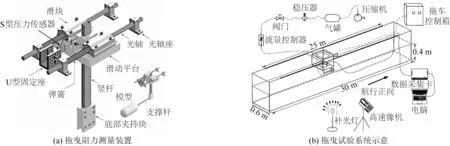
图2 试验系统示意Fig.2 Schematic diagram of the test system

拖曳试验在一个尺寸为30 m×0.6 m×0.8 m（长×宽×高）的拖曳水槽中进行。拖车在水槽两侧长25 m 的水平直线导轨上运行，有效行进距离为22 m，最高运行速度为2.0 m/s，加速、减速时间均为3 s。试验的供气系统由空气压缩机、储气罐、稳压器、阀门与流量控制器组成，通过PU 气管依次连接，最后连接至潜航器的充气尾管。具体过程是空气压缩机提供压缩气体至容积为25 L的储气罐，然后由稳压器滤去来流中的杂质并向后输出压力稳定的气流，最后通过流量控制器主动调节输出气体流量至设定值来实现为模型持续、可控地供给气体。拖曳试验现场各系统整体布置如图2（b）所示。所有试验工况的水深均为0.4 m，潜航器中轴线距离水面均为0.16 m，拖曳速度u则分别为：0.50、0.75、1.00、1.25、1.50、1.75、2.00 m/s。正式试验中在同一拖曳速度下，首先进行非充气工况的模型阻力测量，然后启动供气系统，将供气流量Q调节至10 L/min，进行相应充气工况的阻力测量。

2 数值模型

2.1 控制方程

可压缩黏性两相流的控制方程为：

其中，ρ、U和μ分别为流体密度、速度以及动力黏性系数；p，F为压力和体积力。Navier-Stokes 流动控制方程在雷诺平均（RANS）框架下进行时间平均，并通过引入两个新变量来模拟生成的波动项，即湍流动能k和耗散率ε。两个新的湍流变量由RNG (renormalization-group) k-ε方程［18］来封闭。

使用VOF 方法计算喷射出的微气泡在流体中的运动。液相和气相的体积分数分别用α1和α2表示，满足以下关系：

因此水—气混合物的任何材料特性（例如，密度ρ和黏度μ）φ都可以改写为：

另外使用改进的高分辨率界面捕获（HRIC）方法［19］来重建并捕捉气泡的边界（液相体积分数取值α=0.5）。该方法虽然不能非常清晰地捕捉气—液交界面，但其占用的计算资源更少，满足研究的计算需求。对于可压缩流动，理想气体模型可以写成以下形式：

其中，pop是操作压力，p是相对于操作压力的局部静压，R是通用气体常数，MW是分子量，温度T将根据能量方程计算。

2.2 计算设置

将试验模型后艇体处的支撑结构和充气管去除就得到了图3（a）中用于数值计算的对照模型。另外，在对照模型的头部与试验模型喷气小孔对应的位置，单独划分出5 mm 宽的环状多孔介质区域来等效相距5 mm、孔径0.4 mm 的双排喷气小孔。同时将多孔介质位于潜航器内部的区域设置为气体产生区，通过添加空气质量源项来调整气体的生成速率至10 L/min。数值计算中通过水流运动来等效替代拖曳试验中的模型运动，即认为模型在静水中运动和流体经过静止模型是等价的。整体计算区域如图3（b）所示，所有计算工况中来流速度与试验工况中模型运动速度相对应。

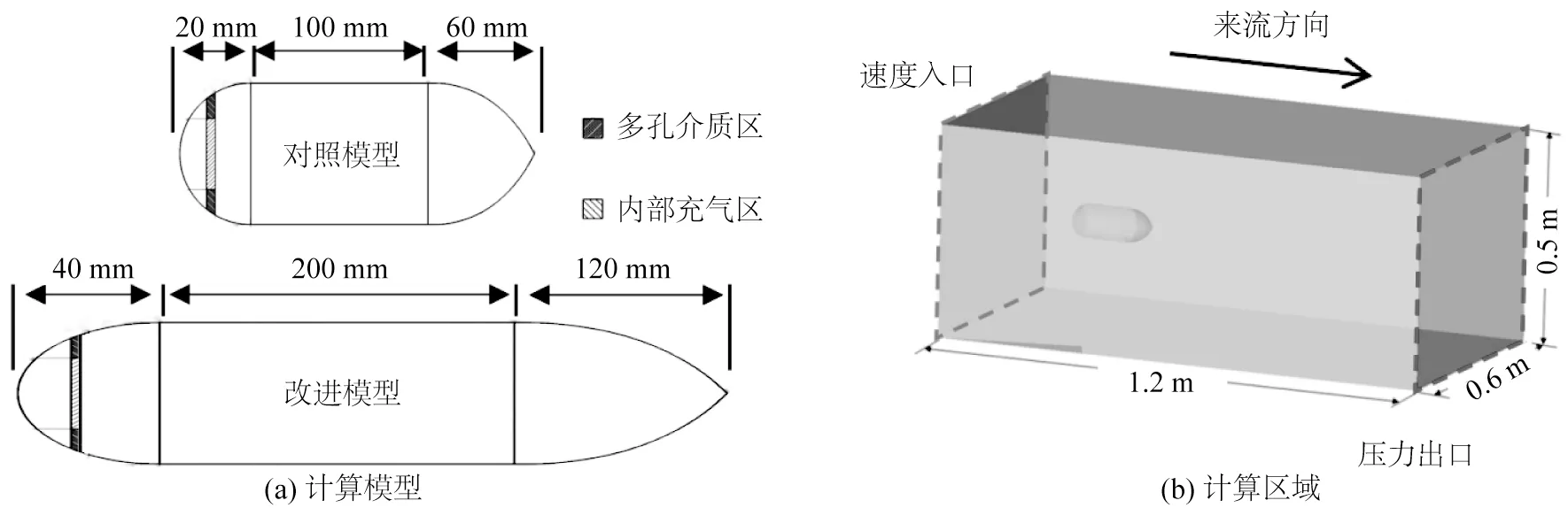
图3 数值计算设置Fig.3 Numerical calculation setup

文中采用ANSYS ICEM CFD 软件对上述计算模型和区域进行结构化网格划分，以对照模型为例的网格划分策略如图4 所示。其中在对模型表面进行网格划分时，将其分成了图4（a）中示意的4 个区域。出气面作为多孔介质区域的外表面，是微气泡产生的核心区域，因此其最大网格尺寸控制在0.5 mm；其余3 个面最大网格尺寸放大至2 mm；网格总量约300 万。模型前方的速度入口边界通过编写的 UDF 文件来控制入口处的水面高度和速度，模型后方及上方边界设置为压力出口，下方底面和左右两侧壁面均为无滑移壁面条件。

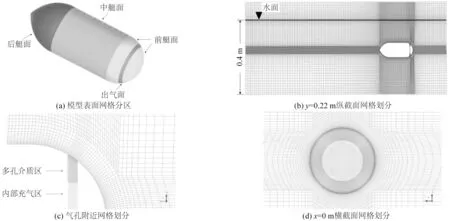
图4 网格划分示意Fig.4 Schematic diagram of the mesh

2.3 数值模型验证

图5（a）中非充气工况的试验数据和数值结果对比显示，当流速小于1.50 m/s时，数值计算得到的模型阻力与试验测量得到的数据非常吻合，然而当流速高于1.50 m/s 时，数值结果开始偏小。这是因为流速过高时，试验模型后艇体处的支撑杆和充气管等装置对流场的扰动增强，影响了模型的压差阻力，使测量得到的阻力值高于计算值。综合来看，文中的三维流场数值模型可以用于潜航器的航行阻力计算。

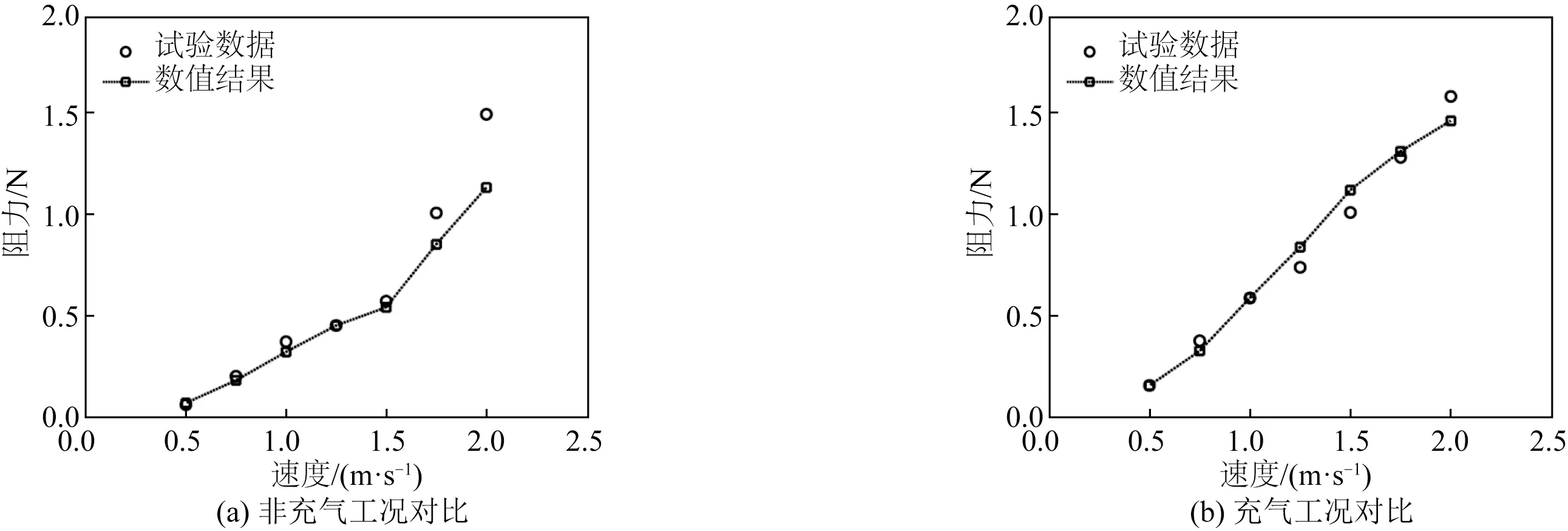
图5 试验与数值对比Fig.5 Comparison of experimental and numerical results

充气试验中，潜航器前盖体内的空气在内外压差的作用下通过多个喷气小孔以离散的微气泡形态喷射入水体，形成微气泡流。数值计算中使用环状多孔介质区域来等效上述喷气小孔就需要对该区域的孔隙率和黏性阻力系数进行调试，使其对气体的阻碍效果和小孔近似。文中以来流1.00 m/s 时充气拖曳试验的阻力数据和高速摄像机得到的模型附近微气泡流形态作为依据进行多次调试。最终确定多孔介质区域的孔隙率为0.3，黏性阻力系数为2 × 1010，这与周照耀等［20］对具有近似孔隙率的不锈钢丝多孔介质进行渗透测试所得到的数据基本相符。将上述参数代入其他充气工况进行验证。如图5 （b）所示，试验数据和数值结果吻合良好，证明了使用多孔介质区域来等效喷气小孔的合理性和双相流数值模型的准确性。

3 试验模型的结果分析

3.1 微气泡流形态特征

通过对比试验和数值计算得到的充气情况下模型受到的阻力，定量评估了采用多孔介质来等效喷气小孔的准确性。除此之外，拖曳试验中气泡流的形态也是一个重要且可观察的物理现象。由于采用的是VOF方法并设置多孔介质区域，数值计算并不能精确捕捉气泡群中的单个离散气泡，但依然可以将数值计算得到的气体分布与实际微气泡流在宏观上的群体特征进行对比。只有当两者的气流运动轨迹相似时，数值模型才能正确地预测气体运动对流场的影响。

图6展示了3种来流速度下试验观测（图6（a）、（b）、（c））和数值计算（图6（d）、（e）、（f））得到的微气泡流典型形态。从高速摄像机拍摄的瞬时图片来看，在速度为0.50 m/s 时，由于流速较低，来流并不能将微气泡压覆于潜航器表面。因此气泡在浮力作用下，快速脱离潜航器，形成图6 （a）中潜航器顶部的上浮气流。当速度提高到1.00 m/s时，大部分气泡在水流冲击作用下开始沿潜航器表面运动并于尾部形成一股尾部气流，这股气流沿流向运动很短的距离就开始上浮。随着速度的进一步提高，上述两股气流的运动轨迹与来流方向的夹角逐步减小。图6（d）、（e）、（f）中使用α2= 0.1 的等值面显示了计算得到的气体在流场中的分布情况。可以看到数值结果不仅能够捕捉到上浮气流和尾部气流，而且两股气流的产生位置和运动轨迹也基本与试验图片相吻合。因此可以认为文中的数值模型能够用于捕捉气泡流的运动轨迹，且计算得到的受气体影响的流场数据也基本可靠；不足之处是未能准确反应气泡群的细节特征。

3.2 潜航器阻力构成随速度的变化

对比于试验测量中只能得到模型的总阻力，将数值结果进行后处理，可以方便、准确地将模型受到的阻力分解为黏性阻力与压差阻力两部分，其中前者是微气泡减阻主要的作用对象。从图7（a）非充气组的数值模拟得的阻力构成占比可以看出，在整个试验速度范围内，黏性阻力与压差阻力两部分之间并未拉开差距，始终处于均势的状态。而图7 （b）充气情况下压差阻力始终占主导地位，占比从开始的79%渐渐上升至86%。这意味着在现有试验工况下，潜航器前端喷射气体形成的微气泡流对试验模型的总阻力构成有显著影响，导致压差阻力成为主要阻力。因此，利用数值结果来显示微气泡对流场的影响，从而研究压差阻力和黏性阻力变化的根本原因，对于微气泡减阻的实际应用是极其重要的。

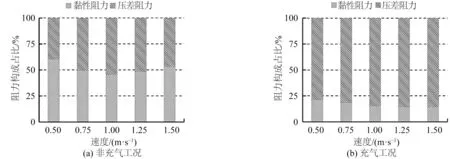
图7 黏性阻力和压差阻力占比Fig.7 Percentage of frictional resistance and differential pressure resistance

3.3 微气泡对压差阻力的影响

图8 展示了模型轴心水平截面上的压力云图和速度等值线的分布。可以明显看到随着来流速度的提高，非充气情况下速度分布具有一定的相似性。主要特征包括：1）结构前端存在半圆形的来流滞止区；2）潜航器中艇体的首尾两个地方存在小范围的高速流动区；3）结构尾部出现了锥状且向后延伸范围较长的低速区域。另外，从扣除静水压的压力云图来看，流场中高于环境水体压力的区域主要集中在模型的前端滞留区和尾部的低速区。随着速度的提升，头部压力升高的同时尾部高压区会逐渐远离模型，导致压差阻力升高。

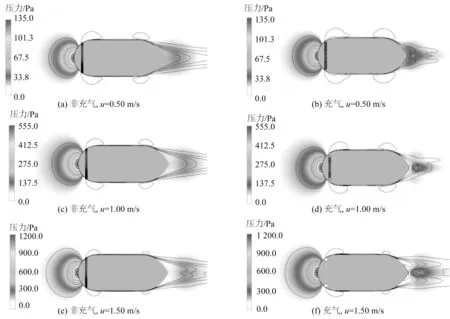
图8 z=0 m 截面处速度等值线和压力云图Fig.8 Velocity and pressure contours at the plane of z=0 m

进一步对比相同来流情况下非充气和充气工况可以发现，喷射的气泡会使得局部流场产生一定的变化。其中除了使艇身中部高流速区的形态发生改变外，最显著的变化是尾部锥状低速区出现大幅收缩现象。且随着来流速度增加，气体对流场的扰动愈加强烈。在1.50 m/s的工况下，尾部开始分裂出2条小尺寸的锥状低速区。正是由于上述尾部流场存在的显著变化，压力场也随之改变。相比于未充气情况，微气泡使得尾部高压区的范围大幅减少，从而导致潜航器的压差阻力上升。因此如何抑制微气泡流对尾流压力场的影响，是进一步提高微气泡减阻效率的关键之一。文中通过改变模型后艇体构型，在一定速度范围内抑制了压差阻力的快速增加，使得充气工况具有更好的减阻效果，该部分将在后续章节详细讨论。

3.4 微气泡对黏性阻力的影响

为研究不同来流速度对微气泡摩擦减阻的影响规律，对流速做无量纲处理，定义来流雷诺数为：

其中，u为入口处的来流速度，D为潜航器的直径，ν是流体的运动黏性系数。因此试验模型对应的Re变化范围为4 × 104～1.6 × 105。另外定义无量纲局部摩擦减阻率η为：

式中：fn为未充气时中艇体的黏性阻力，fg为充气时中艇体的黏性阻力。

图9（a）中黏性阻力的对比结果显示，在固定充气量（10 L/min）的情况下，随着潜航器速度的提高，微气泡在中艇体处的减阻效果逐步提升，这与图6 中观测到的气体在该区域覆盖面积的扩大紧密相关。当速度达到2 m/s时（Re≈1.6×105），局部摩擦减阻率约为65%，说明微气泡流可以有效降低中艇体处的黏性阻力，并且从图9（b）中摩擦减阻率曲线的发展趋势来看，这个数值还将随着来流速度的进一步提高而增加。

图9 对照模型中艇体摩擦减阻效果Fig.9 The drag reduction effect at the middle part of the compared model

虽然潜航器前端气孔喷射出的微气泡可以通过覆盖结构表面来降低黏性阻力，但部分未覆盖的区域或者间歇性与水体接触的部分还是会存在较高的黏性阻力。因此需要通过分析潜航器表面的黏性阻力分布来了解气膜覆盖的效果。图10 显示了未充气和充气情况下，来流速度分别为0.50、1.00、1.50 m/s 时，潜航器表面黏性阻力的分布情况。

在非充气情况下（图10（a）、（c）、（e）），可以明显地观察到结构受到的黏性阻力主要集中在图10（a）中标注的区域1和区域2。并且随着来流速度的增加，阻力最大值相应提高但是分布规律并没有发生变化。这主要是因为前面所提到的非充气工况时流场在不同来流速度下均具有高度的相似性。但是充气情况下的阻力分布（图10（b）、（d）、（f））存在明显变化。首先，气孔喷射的气体对下游一定范围内的遮蔽作用导致区域1中黏性阻力显著降低，因此高黏性阻力的区域1消失。其次，气泡脱离潜航器表面的上浮运动所引起的水流横向运动产生了新的高黏性阻力区域3。由于气泡上浮轨迹是浮力和水流阻力的共同作用结果，所以区域3的形状和位置会随着来流速度的提高而变化。最后，区域2 随来流速度的增加逐步发展为一个主要的高黏性阻力区域，与区域1和3不同的是该区域黏性阻力分布呈现出多峰值特征，而该特征与微气泡在潜航器表面的覆盖效果密切相关。

气体从潜航器前端的气孔喷出后，在浮力和水流冲击的共同作用下产生一个斜向上的运动轨迹。如图11（a）所示，当来流速度较小时浮力作用占优，气泡会快速上浮而脱离结构表面，导致气膜的覆盖区域偏少，从而降低减阻效果。随着来流速度的提高，高速水流可以将气体强制压覆在结构表面，使得气膜覆盖区域扩大，提高减阻效果。在文中的工况下，当来流速度提升至2.00 m/s 时，气体仍然不能完全覆盖潜航器中艇体部分。模型未被气泡覆盖处由于与水体接触，黏性阻力会高于被气泡覆盖的区域，这就导致了区域2中黏性阻力分布具有多峰值特征。另外，正是由于气泡未能包裹模型整体，所以图6（b）中局部减阻率在2.00 m/s的工况时仍处于快速增加的阶段。继续提高来流速度，局部减阻效率会进一步提高，直到气泡对潜航器形成一个全面的包裹。

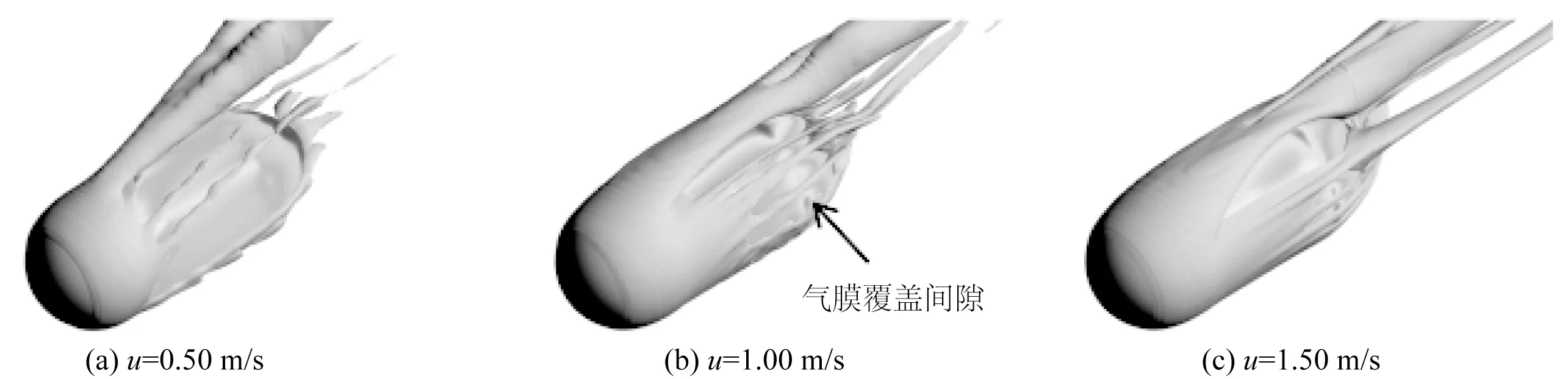
图11 潜航器表面气膜分布Fig.11 Distribution of bubbles film on the surface of the underwater vehicle

图12（a）～（c）从俯视角度展示了不同来流速度下潜航器表面附近三维流线的分布特征，其中潜航器中艇体上侧为水—气体积分数云图，下侧为壁面剪应力分布云图（两部分之间用虚线分隔）。从图12 （a）中可以明显看到，受到气体影响的水流在气孔下游区域发生了流动横向偏转现象，具体表现为结构侧边的流体向结构上方运动。而正是这种偏转运动导致了图10（b）、（d）、（f）中结构表面对应部分存在较高的黏性阻力。进一步通过图12 （d）中的压力分布（扣除静水压）可以看出，潜航器顶部上浮气流形成的遮蔽区附近存在两侧对称的低压区和高压区。原本流经高压区的流体在受到阻碍后转向附近的低压区导致了上述流体横向偏转现象。

图12 潜航器附近三维流线及压力分布Fig.12 3D streamlines and pressure near the underwater vehicle

4 改进模型的微气泡减阻

为了研究微气泡减阻的实际应用价值，以对照模型为基础增加了中艇体的长度，并对后艇体进行外形优化得到了图3 （a）中的改进模型。计算结果表明上述改进措施可以有效降低微气泡对压差阻力的影响，从而达到模型整体阻力下降的减阻效果。相比于对照模型，改进模型在同一深度处进行了更高流速的数值计算，来流速度范围：1 m/s至5 m/s，对应的Re范围：8 × 104至4 × 105。另外定义模型整体阻力系数为：

式中：F为潜航器的总阻力，A为模型沿来流方向的投影面积。

图13中模型阻力系数随来流雷诺数的变化表明速度在2 m/s至4 m/s之间时，微气泡产生了整体减阻效果。在u=3 m/s 时减阻率约为16.8%，证明了微气泡减阻的可行性。然而当来流速度在前述范围之外时，微气泡仍使得模型阻力系数增高。主要原因是在低速状态下，气泡覆盖潜航器的面积不够；而高速状态下，微气泡干扰尾流所引起的压差阻力增量大于黏性阻力的减少。这表明气体对尾流场的影响程度不仅与潜航器的尾部外形有关，还取决于来流速度。由于微气泡和尾流场存在这种复杂关系，因此在试验前的模型设计阶段，数值模拟对于潜航器的外形优化具有重要意义。

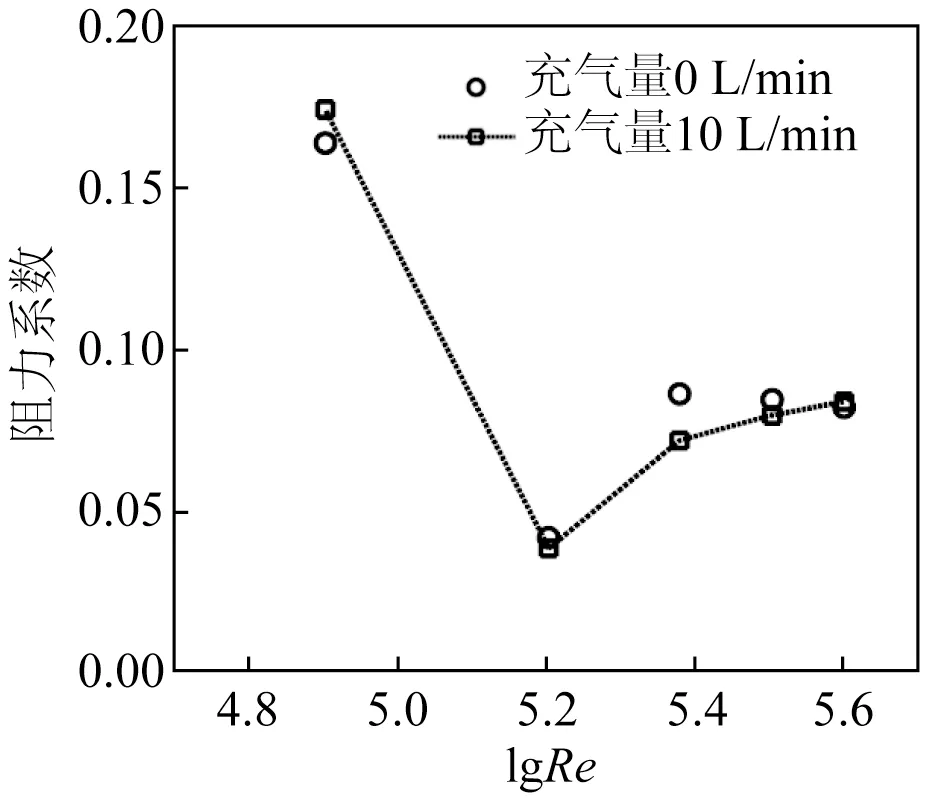
图13 改进模型的阻力系数随Re变化Fig.13 Resistance coefficient of the modified model changing with Re

5 结 语

以回转体潜航器简化模型为研究对象，利用试验数据证明了采用VOF 多相流模型与k-ε 湍流模型来计算水下微气泡减阻问题的可靠性以及多孔介质等效喷气小孔的合理性。并基于数值结果进一步分析了充气情况下潜航器的阻力变化及根本原因，主要结论为：在相同来流速度的情况下，微气泡会显著影响尾流处的低速区，使得尾部低压区的面积扩大导致压差阻力升高。同时微气泡也可以有效降低模型被气泡覆盖区域的黏性阻力，且局部减阻率随着速度增加而提高。

值得注意的是，微气泡流的存在并非对整个模型表面的黏性阻力都有降低效果。其中对被气泡包裹的模型表面具有明显的减阻效果，而未包裹的部分由于流场的改变，黏性阻力分布相较于未充气情况有着很大的变化。首先是中艇体后端较高黏性阻力区域出现点状分布特征，其次是中艇体出现条状高阻力区域。前者是由于气膜在尾部对结构表面的覆盖存在空隙，而后者是因为气体的干扰使得潜航器中部的流体运动存在横向偏转。因此如何通过合理安排气孔位置和前艇体几何外形来降低上述现象引起的黏性阻力增加是接下来的研究方向。

另外，通过优化潜航器后艇体构型可以在一定速度范围内降低气泡运动导致的压差阻力升高，从而达到整体减阻的效果。但随着流速进一步提高，气泡引起的压差阻力显著增加，最终导致模型阻力系数高于非充气情况。这表明由于气泡流的存在，尾部流场的状态与流速之间存在复杂的关系，需要进一步的试验和数值研究。