对初中数学概念教学的思考与实践

邹晶

［摘  要］ 数学概念是数学知识体系的核心要素，学好数学概念是学好数学、用好数学的前提. 在概念教学中，教师应改变传统“照本宣科”的讲授式教学模式，通过创设情境、设计探究活动等方式来揭示概念的本质，引导学生经历概念形成和发展的过程，从而领悟数学学习的本质，提升数学学习能力.

［关键词］ 数学概念；本质；学习能力

数学概念具有高度概括性，初中生的知识储备有限，自我剖析文字能力较弱，因此他们面对高度概括的数学概念时难免会产生畏难情绪. 虽然学生通过自主学习能够熟记概念，但是他们对概念的理解仅停留在表面的文字内容上，并不能很好地把握数学概念的内涵及外延，所以引导学生理解和掌握数学概念，是每个数学教师必须完成的教学使命. 但实际教学中，部分教师对概念教学存在片面的认识，他们认为学生只要会背概念，能用概念解决问题即可，因此教学时他们常常将概念直接抛给学生，然后给出相应的练习帮助学生理解和消化. 不可否认，应用概念是深化概念理解的重要手段，但是教学中若仅仅照本宣科和照抄照搬，将难以激发学生学习数学的积极性，不利于学生创新能力的培养. 因此，在概念教学中，教师必须改变传统观念，通过创设合适的教学情境带领学生经历概念形成和发展的过程，让学生更好地把握概念的本质，并通过多种手段拓展概念的外延，让学生在理解和掌握概念的基础上能灵活地应用概念解决问题. 下面笔者结合教学经验，谈几点教学体会，供各位读者参考.

更新概念教学理念

随着新课改的不断深入，数学教学越来越关注学生终身学习能力的培养，因此，在平时的教学中，教师必须打破传统的“灌输”式教学模式，通过合理的启发和引导让学生学会学习. 在概念教学中，教师要为学生营造一个和谐的、互动的学习氛围，鼓励学生探寻概念背后的价值，从而深度理解概念，激发学生的数学学习兴趣.

1. 创设情境，激发兴趣

数学概念是从生产生活中不断抽象、概括得出的，其具有高度的抽象性. 为了让学生更好地理解抽象的概念，教师可以适时地引入一定的情境，化抽象为具体，有效地激发学生的学习兴趣.

例如，在概念教学中，教师可以引入一些生活实例，或引入相关的数学故事，抑或是数学趣闻等. 恰当情境的引入，不仅可以增强数学的趣味性，而且能引发学生思考，实现以学生为主体的教学目的.

2. 深度探究，把握实质

概念教学若仅仅停留在咬文嚼字上，那么概念教学是枯燥乏味的，不利于激发学生的数学学习兴趣. 其实对于学生是否掌握概念，我们看的并不是学生是否熟背概念，而是看学生是否掌握了概念的本质. 在概念教学中，教师要充分发挥引导作用，通过类比、实验、操作等方式来揭示概念的实质，从而提高学生的数学应用能力.

例如，学习“一元一次方程”的概念时，学生不需要一字不漏地熟背概念，只需要把握三个关键词，即一元、一次、整式，对于把握关键词，学生不仅易于理解和记忆，而且能将经验迁移至一元二次方程、二元一次方程组、一元一次不等式等概念的学习中，有利于知识体系的建构.

把握概念教学的尺度

教材是数学专家精心编写的，具有典型性、系统性、普适性等特点，其在教学中的价值不言而喻. 不过，若数学教学仅停留在以本为本、以纲为纲的层次上，恐怕难以激发学生的潜能，不利于教师教学水平的提高，所以教师教学时，教学内容应有所取舍，且应从教学实际出发，把握好教学的梯度和深度.

1. 把握概念教学内容的梯度

众所周知，人的认知发展遵循由浅入深、由易到难的循序渐进过程，学生对概念的理解亦是如此. 在教学中，教师要认真研究教材，对教材中的相关概念进行整体把握，重视各部分概念间层层递进的关系，做到讲解到位但不越位，从而提升教学的有效性.

例如，对于绝对值的概念，教材虽然对其几何意义做了说明，但大多数学生依然模模糊糊的. 学习“二次根式”时会再次涉及绝对值的概念，此时可以用开平方运算来理解绝对值的概念，让学生进一步理解绝对值概念的实质. 学习“函数”知识后，教师可以让学生画出y=x，y=x－4，y=x2－4的图象，并借助图象进一步理解绝对值的概念. 相信通过以上分层探索，学生能将绝对值的概念学懂、吃透.

在教学中，教师切勿急于求成，要按照概念的层级特点进行梯度教学，要顺应学生的发展规律，让学生的学习能力和思维能力螺旋上升.

2. 把握概念教学内容的数量

受传统讲授式教学模式的影响，部分教师为了让学生更好地理解概念，认为概念教学的内容讲得越多越好，讲得越仔细越好，在概念教学中追求面面俱到. 其实学生理解和消化知识需要经历一定的过程，学生的认知过程也有一定的规律，所以教师在教学中应顺应学生的发展规律，为学生提供一些需要探索、思考的教学内容，为学生创设一个自由思考的空间，以促进学生全面、持续、和谐地发展.

例如，在“因式分解”的概念教學中，在学生尚未掌握前面部分概念的应用的情况下教师就直接讲解可以在哪种数系范围内进行因式分解、分解为哪种形式，这样的教学过程看似系统、完整，却大大增加了学生的认知难度，会影响学生的数学学习信心.

注重概念教学的方法

学生学习能力的提升难以通过“灌输”来达成，它需要经历一个长期且复杂的过程，需要学生自己去感悟、去思考、去探究. 因此，在概念教学中，教师应带领学生经历观察、实验、猜想、推理、抽象等过程，让学生更好地把握概念的本质，从而提高学生独立思考和探索问题的能力，落实学生的数学核心素养.

1. 重视概念本质的揭示

日常教学中经常出现如下情况：学生虽然能够将概念、定理等背得滚瓜烂熟，但具体应用时却常常“张冠李戴”. 究其原因，是学生没有理解概念的本质. 因此，在教学中教师应重视概念本质的揭示.

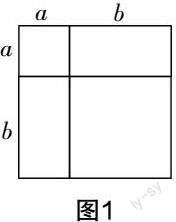
例如，学习乘法公式（a+b）2=a2+2ab+b2后，教师呈现一些练习题帮助学生巩固公式. 从学生的做题情况来看，他们在运用公式时常常漏掉2ab这一项. 如：（a+2）2=a2+4，（m+n）2=m2+n2. 分析错因不难发现学生并未掌握公式的本质. 为了深化学生对知识的理解，教师将公式转化为图形（如图1所示），借助图形的直观来揭示公式的本质.

给出圖形后，教师让学生观察、交流. 学生观察图形后发现，对于边长为（a+b）的正方形，其面积除了边长为a的正方形和边长为b的正方形的面积而外，还有2个面积为ab的长方形. 上述过程借助图形的直观将抽象的代数概念具体化，揭示了概念的本质，促进了概念的深化，发展了学生的数学思维.

2. 重视概括概念的过程

概念揭示的是事物的本质特征，具有抽象性等特点. 在概念教学中，教师应采用正确的教学方法将概念形象地展示出来，让学生通过观察、探索、交流等方式体验概念形成和发展的过程，引导学生进行概念抽象. 经历上述过程，学生便能更加清晰、牢固地掌握概念. 另外，引导学生经历概念的抽象既有利于提高学生的抽象概括能力，又能培养学生思维的深刻性和严谨性.

例如，教学“单项式和多项式”的概念时，教师没有直接给出概念，而是出示如下问题让学生总结归纳. 问题如下：

（1）观察式子－2x，2a2，ab，xy/2，它们是如何组成的？有什么共同特点？

（2）观察式子－2x+3y，2a2+3ab－b2，a2+3a－5，它们是如何组成的？与（1）相比这些式子有何共同特点？

借助具体问题情境让学生观察、分析、交流，并引导学生对信息内容进行概括，能锻炼学生的抽象素养，能提高学生的数学学习能力.

注重概念教学的手段

随着时代的发展，信息技术的普及为数学课堂带来了新的气息. 在概念教学中，教师可以形象地呈现概念的形成和发展过程，使抽象的、枯燥的概念教学变得具体、生动，从而提升概念教学的有效性，提高学生的数学学习兴趣.

总之，教师进行数学概念教学时，不能简单地将概念的文字内容呈现给学生，应重视概念本质的揭示，让学生掌握研究数学的方法，从而提高学生的学习品质，培养学生终身学习的能力.