边界层分离再附着效应对板式换热器传热特性的影响
2023-08-21余建平田有文沈文朋
余建平 田有文 宋 伟 朱 钰 沈文朋
(1.兰州理工大学石油化工学院;2.天华化工机械及自动化研究设计院有限公司)
在“碳达峰、碳中和”的背景下,板式换热器以其结构紧凑、对数平均温差大、压降低、换热效率高等优点,在分布式能源、可再生能源、空调及供暖等领域得到了高度关注[1,2]。通过改变板片形状、增大换热面积、强化流体扰动可以实现板式换热器的强化传热,进一步提高板式换热器的传热性能,其典型产品有V型槽、波纹板、鼓泡型等板式换热器[3]。大量的实验及工程实践表明,换热器表面的褶皱和突起具有强化换热的作用,然而多样的板型结构是如何起到强化换热作用的还不明确,而相关理论的缺乏又导致板型结构设计没有统一的理论指导。
笔者从流动非稳定性理论入手,建立边界内强化换热理论机制,分析曲线板片在逆压梯度作用下边界层分离与再附着对板片换热的影响,探讨板式换热器线型设计的理论方法。
1 边界层分离再附着理论
由场协同理论[4,5]可知,当流场中速度场U→与温度梯度∇T的夹角垂直时,即U→·∇T=0时,流动对换热不起作用,流动传热问题将演化为纯导热问题。在层流流动条件下,边界层内流体流动方向与热流方向几乎垂直,此时,流动不能起到强化传热的作用,边界层成为热阻的主要来源。
为了实现强化换热,考虑从减薄边界层入手。在曲面边界条件下,逆压梯度将导致边界层减薄并分离,从而起到强化换热的作用,这个现象在横掠圆柱等实验中已被观察并证明[6]。
简化后的边界层方程如下:
其中,u、v为x、y方向的速度;ρ为流体密度;p为流体压力;ν为运动粘度。边界层方程的非线性特性导致其难以求解,冯·卡门在方程组(1)的基础上引入边界层位移厚度和动量亏损厚度,建立了线性积分形式的边界层方程,使得边界层问题得以简化:
其中,τw为壁面切应力;U为外流速度;θ为动量损失边界层厚度;δ*为位移厚度。
卡门动量积分方程是对于层流和湍流均适用的精确方程,方程给出了主流场速度、边界层结构与壁面摩擦力之间的定量关系,但并未给出边界层内的速度分布形式,还需要假设速度分布才可以进行边界层分析。
1921年,Pohlhausen提出了5系数(a、b、c、d、e)的曲面边界层速度假定:
其中,η为边界层厚度,无量纲;δ为边界层厚度。
根据边界层已知的边界条件可以得到5个系数的表达式:
其中,Λ是波尔豪森参数(无量纲),反映了外部势流压强梯度对边界层内部流动的影响。
Pohlhausen在理论上解决了边界层分离点的判定问题,但实验测试表明,Pohlhausen理论预测方法准确度不高。为了进一步提高边界层分离点的准确性,1940年Holstein和Bohlen提出用新的无量纲数λ来代替波尔豪森参数,此时动量积分方程(2)可简化为:
其中,U′为外流速度在x方向的分量。1949年,Thwaites在分析大量实验数据后提出了F(λ)的计算方法,即:
由此式(9)可改写为:
式(11)为积分形式的动量边界层分离方程,当给定边界层外缘势流的速度分布后,可由式(4)求出θ,进而求得λ,当λ=-0.09时壁面切应力为0,由此可求得边界层分离点位置。
2 板型曲线函数
为了达到控制边界层分离的目的,引入二维数学方程表示板型曲线。该曲线为一光滑渐缩渐扩的由Gamma函数构成的曲线,其数学方程为:
其中,系数α用于控制曲线的高低,系数β用于控制曲线的宽窄,Γ(α)为Gamma函数。
3 模型求解及验证
3.1 分离点的理论求解
由质量守恒方程可求出流速与截面的对应关系:
根据势流理论,外边界层压力与速度关系可由伯努利方程求出:
其中,P为外边界层压力。将式(13)与式(4)联合即可求解出边界层分离点的位置。由于边界形状曲线为一非线性函数关系,故还需采用数值法求解动量厚度和边界层分离点位置。
3.2 分离点位置的数值求解
为了检验Thwaites理论预测边界层分离点位置的准确性,进一步分析板式换热器内的流动传热情况,建立二维板式换热器模型,方程系数选择α=1、β=0.5。模拟方案采用倒置式流道,即上表面为光滑无摩擦表面,用于提供主流区压力梯度,下表面为无滑移壁面条件,用于计算边界层分离及再附着点。计算区域入口为速度入口边界,出口为压力出口边界。采用有限体积法进行离散求解,壁面热边界为恒温壁面。
3.3 分离点位置的可靠性验证
为了确定数值模拟的可靠性,将不同Re数下的边界层分离点数值模拟结果与不同研究者的实验数据进行对比,结果列于表1。可以看出,Thwaites理论解与数值解、实验解[7]三者基本一致,由此验证了数值分析法和Thwaites理论模型的可靠性。
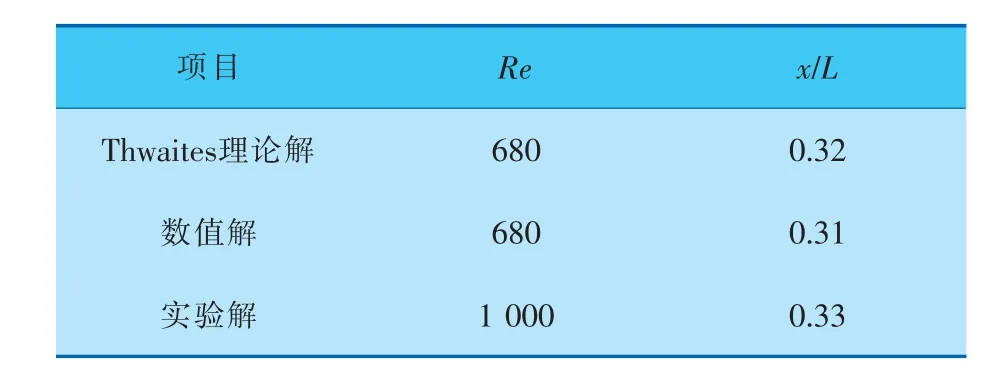
表1 分离点位置与实验数据对比
4 分析与讨论
4.1 边界层分离点
边界层分离点是壁面切应力为0的点,图1给出了沿x方向壁面的摩擦阻力系数曲线。由图1可以看出,边界层分离点受到来流Re数的影响,但是影响作用不大;层流条件下Re数从170增大到680时,边界层分离点由x/L=0.35向上游移动到x/L=0.31。边界层分离点相对固定,表明在来流速度变化较大时现有的曲线表面能较好地适应来流变化,边界层分离点不会因为来流速度的变化而失去控制。

图1 沿x方向壁面的摩擦阻力系数曲线
4.2 分离再附着区的特性
在逆压梯度的作用下边界层会出现分离,同时还伴随着流动的继续、流道扩张、流速下降,当逆压梯度消失后边界层会重新附着在壁面上。边界层在分离及再附着的过程中,流体壁面附近会出现一个被拉伸的漩涡,称为分离泡[8~13]。图2给出了不同Re数下的分离泡形态图。
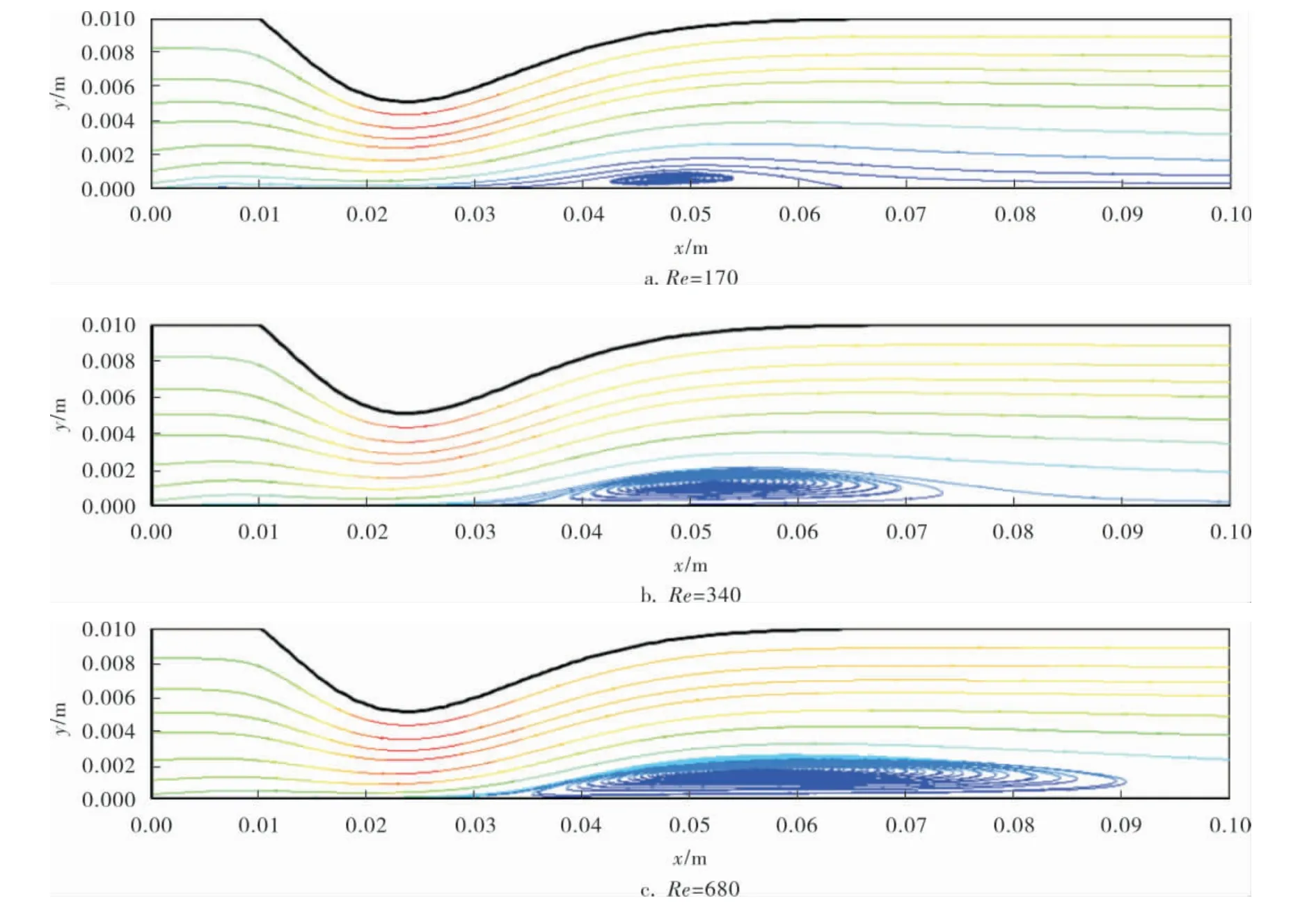
图2 不同Re数下的分离泡形态图
由图2可以看出,随着Re数的增大分离再附着区域变大,分离泡长度与Re数之间呈现出正比例线性关系,回归两者的关系可得如下近似关系式:
其中,下角标c代表参考值。
4.3 分离区的换热特性
图3给出了不同Re数下的x方向壁面Nu数曲线。可以看出,当壁面的对流换热系数受到曲面壁面的影响时,壁面对流换热系数并非均匀减小,在曲线喉部,由于流体速度增大,壁面对流换热系数在较大范围内保持在恒定状态,而随着流道的扩张,流速下降,壁面Nu数快速下降,当进入到分离泡核心区域时,壁面对流换热系数下降到最小值;壁面对流换热系数受来流速度的影响较大,当来流速度较大时,壁面Nu数也较大,这与传热边界层理论分析相一致。为了便于比较未分离壁面与分离壁面的换热系数,从图3中纯平壁在Re=680时的对流换热系数曲线可以看出,在曲线边界条件下以及在边界层分离点之前,壁面对流换热系数大于纯平壁的;而在边界层分离之后形成的分离泡区域,其Nu数远小于纯平壁的。
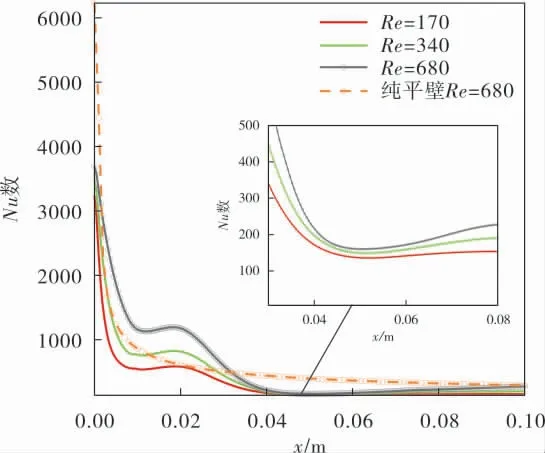
图3 不同Re数下的x方向壁面Nu数曲线
通常,流场中涡的出现会起到强化传热的作用。但是,数值计算表明,边界层分离后产生的分离泡不仅不会强化换热,反而会削减传热,分离泡核心区对流换热系数将达到最小值。分离泡内部的流场及温度分布云图如图4所示,可以看出,分离泡是一个封闭的涡旋结构,它并不能起到掺混冷热流体的作用。外侧的来流将越过分离泡继续流动,而分离泡的出现,相当于增加了边界层的厚度。
5 结束语
笔者建立了用于描述板形曲线的参数方程,通过控制曲线参数可以实现边界内逆压梯度的调节,进而实现流场控制、强化传热。研究结果表明:
a.与数值求解流动传热N-S 方程相比,Thwaites理论相对计算量较小,对于预测层流边界层分离有较高的准确度,可被应用于板型设计中;
b.曲线边界导致流道收缩、流速加快、边界层减薄是曲线板型强化传热的根本原因;
c.边界层分离泡减弱了对流换热效果,同时增加了边界层的厚度,使导热的热阻更大。
