干气密封滑动摩擦界面摩擦振动理论分析及实验测试

孙宝财 张正棠

（甘肃省特种设备检验检测研究院）

符 号 说 明

Aa——名义接触面积，mm2；

CN——法向接触阻尼，N·s/m；

CT——切向接触阻尼，N·s/m；

D——分形维数；

E1、E2——两种材料的弹性模量，Pa；

E——当量弹性模量，Pa；

f——摩擦因数；

G——特征尺度，m；

G1、G2——两种材料的剪切模量，Pa；

G——当量剪切模量，Pa；

KN——单微凸体法向接触刚度，N/m；

KT——单微凸体切向接触刚度，N/m；

lb——基底长度，m；

P——单微凸体上法向载荷，Pa；

Qx——单微凸体上切向力，Pa；

V——动环滑动速度，m/s；

α——螺旋槽根径；

μc，t——切向与法向阻尼比；

μk，t——切向与法向刚度比；

ν1、ν2——两种材料的泊松比。

干气密封是动设备中应用广泛的非接触式密封。在密封系统稳定运行时，干气密封会在动环与静环之间产生一个具有一定刚度和一定厚度的气膜［1，2］以达到预定的密封效果。但是在实际运行中，特别是在干气密封系统的启动和停止期间，动环和静环端面间不可避免地会发生接触，这主要是受加工制造水平达不到精度要求、装配过程存在误差及工况等因素的影响［3］。这种接触摩擦会使动环和静环端面间产生失效，严重影响干气密封系统的使用寿命，甚至可直接导致干气密封系统失效，从而造成极大的危害［4，5］。

目前，研究学者们均是在干摩擦状态下对机械摩擦副的粘滑和纯滑动引起的振动问题进行探讨［6～12］，由起初的单自由度系统逐渐发展研究到两自由度系统［13～17］，所涉及的摩擦模型也逐步从静态摩擦模型向动态摩擦模型过渡［18～22］。在试验测试方面，丁雪兴等通过对螺旋槽干气密封环进行摩擦性能试验，分析了不同工况下的密封环磨 损 量 与 摩 擦 系 数 之 间 的 变 化 规 律［23，24］。HUANG W F在干气密封的启动和停止期间，采用声发射技术进行试验测试，但未见有关干气密封摩擦界面摩擦振动试验测试方面的报道［25，26］。笔者在干摩擦状态下分析干气密封系统动环与静环端面间的受力情况，通过分形理论相关知识考察微观形貌与接触特性对系统的影响，从而建立两自由度摩擦振动系统模型，并搭建相应的实验平台来测试模拟摩擦振动信号，将所得结果与理论计算值进行对比，为进一步研究干气密封接触摩擦奠定理论基础。

1 理论模型的构建

1.1 摩擦振动系统物理模型

干气密封系统中摩擦副是在动环与静环没有润滑状态下相互接触摩擦形成的，动环端面在法向载荷P的作用下沿着静环端面滑动。对静环端面来说，滑动摩擦产生的切向力Qx在整个接触面内平行于x轴，并与动环端面滑动方向相同。两密封端面相对滑动过程中，在P与Qx的共同作用下，在整个接触面内，一部分微凸体处于塑性接触状态，在接触过程中耗散接触力所做的功，表现为阻尼作用；另一部分微凸体处于弹性接触状态，在接触过程中发生弹性变形而存储接触力所做的功，表现为刚度作用。此外，两密封端面相对滑动过程中，静环端面微凸体的起伏将会引起动环在法向（z轴方向）的振动，因此需要考虑微观形貌对摩擦振动的影响。为了研究方便并简化问题，笔者做出如下假设：

a.将干气密封系统动环与静环端面间摩擦界面的接触简化为滑动理想刚性光滑平面与固定粗糙表面的接触；

b.为表征干气密封系统动环与静环端面间摩擦界面在滑动过程中微凸体起伏引起动环在法向（z轴方向）的振动，假定静环的粗糙表面按分形参数构成余弦规律变化；

c.将摩擦振动分为正交的两个方向，即垂直于密封端面的法向（z轴方向）和平行于密封端面的切向（x轴方向）；

d.作为矢量的接触刚度可以分为法向接触刚度和切向接触刚度；

e.作为矢量的接触阻尼可以分为法向接触阻尼和切向接触阻尼；

f.以动环为摩擦振动研究对象。

基于以上假设，抽象并建立了干气密封系统在干摩擦状态下考虑微观接触特性对宏观系统影响的两自由度摩擦振动系统模型，如图1所示，其中Qx=fP。

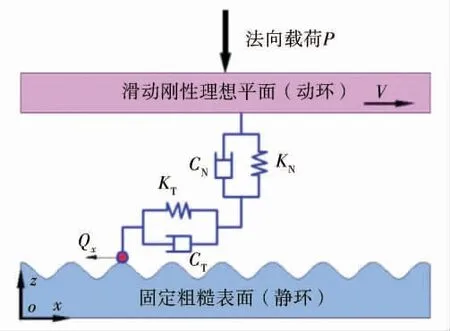
图1 干气密封两自由度摩擦振动系统模型

1.2 摩擦振动法向位移激励

两密封端面在滑动过程中，静环端面微凸体的起伏会引起动环在法向（z轴方向）的振动，即微凸体起伏引起的法向位移为激励。因此，需要构建密封端面法向位移激励的表达式。

具有分形特征的粗糙表面的轮廓曲线可用W-M函数来描述［27］，其数学表达式如下：

其中，L为取样长度，轮廓曲线的空间频率γn=1.5，n为空间频率系数，nmax=int［lg（L/Ls）/lg γ］，Ls为截止长度，通常近似为材料的原子间距离。

1.3 摩擦振动系统数学模型

基于干气密封系统动环与静环端面间振动系统物理模型与法向位移激励，在没有任何润滑介质的条件下，建立两自由度摩擦振动系统数学模型，该模型充分考虑了微观形貌与接触特性对系统的影响。对于图1所示的系统，其动力学方程为：

动力学方程（5）包含接触阻尼、接触刚度和激励，更接近实际情况。但鉴于有阻尼系统在稳态情况下，由于阻尼的存在，系统总响应中自由振动分量很快被衰减殆尽，因此，文中暂时只考虑无阻尼下系统的稳态解。则式（5）在不考虑阻尼的情况下为：

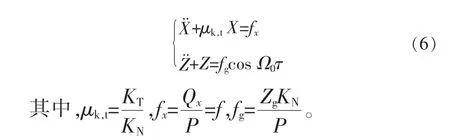
对于式（6）中μk，t所涉及的切向接触刚度与法向接触刚度，分别根据文献［29，30］中的公式进行计算。通过分析可以发现，切向接触刚度与法向接触刚度的比值为定值，且与材料本身有关，即：

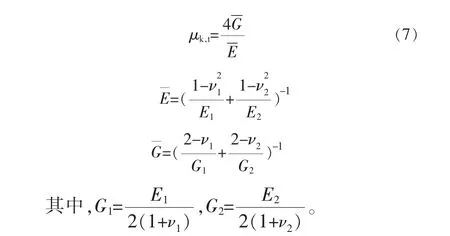
2 理论计算与实验测试

2.1 实验试件

根据被密封介质特性（如材料硬度、强度、导热性、耐腐蚀性、耐高温性、化学稳定性及润滑性等）、操作工况等实际情况，选择端面螺旋槽干气密封系统作为实验测试对象，选择碳化硅作为动环材料、石墨作为静环材料，两者的物理特性见表1。

实验试件需要根据优化的实验方案及要达到的实验目的，并结合试验机的实际情况和启动阶段的工况参数综合设计、加工而成，据此设计的实验试件实物如图2所示。

2.2 实验测试工况

由于实际运行过程中的摩擦难以捕捉，故本次实验测试是基于短暂的启动阶段进行的，即对干气密封系统刚开始运行，端面间尚未形成稳定的刚性气膜前（闭合压力大于密封气体动压力）端面间处于接触状态时产生的摩擦振动信号进行实验测试。根据本课题组前期实验测试的经验和干气密封制造企业的工程实践积累，结合本次实验测试的具体情况，确定实验测试的开启比压为0.10～0.55 MPa，开启线速度为0.55～1.75 m/s。本次实验测试设定为5组载荷、3组转速交叉进行，以其中1种载荷和1种转速的组合工况为1组实验参数（共计15组）进行摩擦振动实验测试，名义接触面积为1 634 mm2，每组工况测试时间10 min，具体参数见表2。

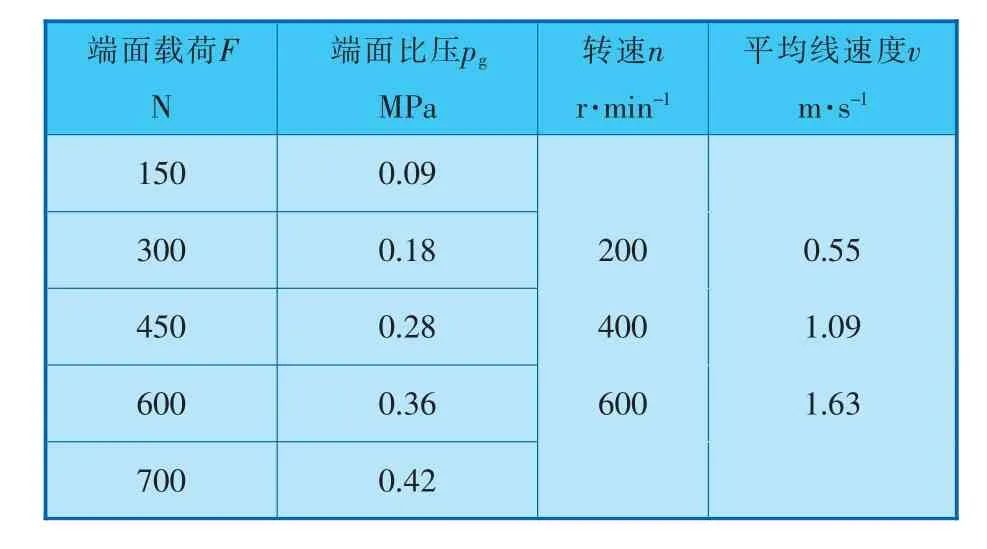
表2 实验测试工况参数

2.3 理论计算

根据建立的干气密封两自由度摩擦振动系统模型、实验试件和工况参数，经过计算、谐波小波包变换后可以得到载荷为450 N、转速为200、400、600 r/min时的摩擦振动信号时频域图。

不同工况下，理论模型计算频率在6 000～6 800 Hz范围内变化，其只与摩擦副 （动环与静环）的材质有关而与载荷、转速等实验条件无关。理论模型计算振幅在切向以10-8m量级变化，在法向以10-6m量级变化。这是因为法向接触刚度大于切向接触刚度，且z方向计算振幅由法向载荷P决定而x方向计算振幅由切向力Qx决定。由此可见，理论模型计算体现了干气密封摩擦振动高频率、低幅值的特征。将载荷固定，理论模型中计算振幅在x、z两个方向上均随转速的增大而增大。这是因为转速的大小可以表征单位时间内一个粗糙表面上的某个特定微凸体相对于另外一个粗糙表面上可能与它相互碰磨的其他微凸体所发生接触次数的多少，这也从另外一个层面反映出摩擦振动振幅将随着转速而改变。

2.4 实验测试

2.4.1 实验测试系统

本次实验测试的主要参数有载荷、转速和摩擦振动信号。其中，摩擦振动信号是通过安装在静环上的高精度加速度传感器、高速采集卡和LABVIEW信号采集系统测得，如图3所示。

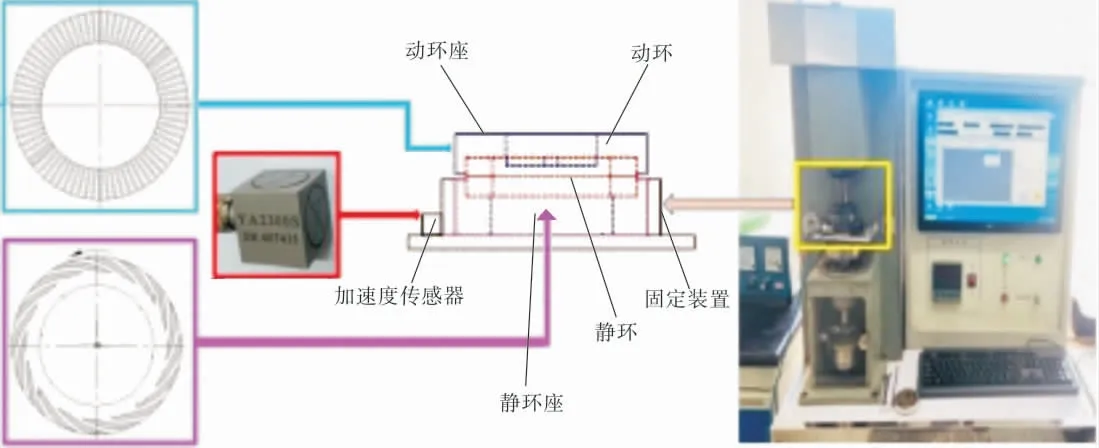
图3 摩擦振动信号采集系统

由于本次实验测试的摩擦振动属于高频微幅振动，其特点是振动加速度大、位移小，因此采用电压灵敏度高、频率范围大的YSV2303S型加速度传感器拾取振动信号。USB46161CP型采集卡采样频率为1 Hz，采集卡与编程软件（支持Win10系统）组成摩擦振动信号测试系统，如图4所示。

图4 摩擦振动信号测试系统

在立式万能摩擦磨损试验机上安装数据采集传感器，具体位置如图5所示。

图5 传感器安装示意图

2.4.2 原始摩擦振动信号

转速400 r/min、载荷450 N时的原始摩擦振动信号中，x方向为滑动摩擦界面的径向方向；y方向为滑动摩擦界面的切向方向；z方向为垂直于滑动摩擦界面的方向。该原始摩擦振动信号中既包含了干气密封系统动环与静环端面间的摩擦振动信号又包含了系统机械振动信号。

原始摩擦振动信号中较高振幅信号的频率主要集中在0～7 000 Hz、12 500～16 800 Hz范围内。x、y、z方向上整个频带存在明显的倍频现象，振 动 基 频ω 为5 768、5 985、5 894 Hz，3 倍 频 为18 925、18 993、18 957 Hz，4倍频为23 514、23 494、23 496 Hz，5倍频为29 845、29 495、29 668 Hz，均表现出周期性变化。微弱的干气密封高频微幅摩擦振动特征完全淹没在原始摩擦振动信号中，无法有效识别出干气密封系统动环与静环端面间的摩擦振动信息，因此，必须采用可靠的方法（如谐波小波包变换）来有效提取动环与静环端面间的摩擦振动信号特征信息。

2.4.3 摩擦振动信号提取与识别

根据理论计算模型得出不同工况下的计算频率，相应的对相同工况下的实验测试摩擦振动信号，采用谐波小波包变换在MATLAB软件中进行5层32个频带分解（带宽为1 000 Hz），得到与理论模型计算频率相对应的时频域图，如图6～8所示。

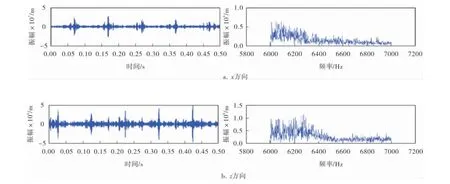
图6 转速200 r/min、载荷450 N时的实验测试时频域图

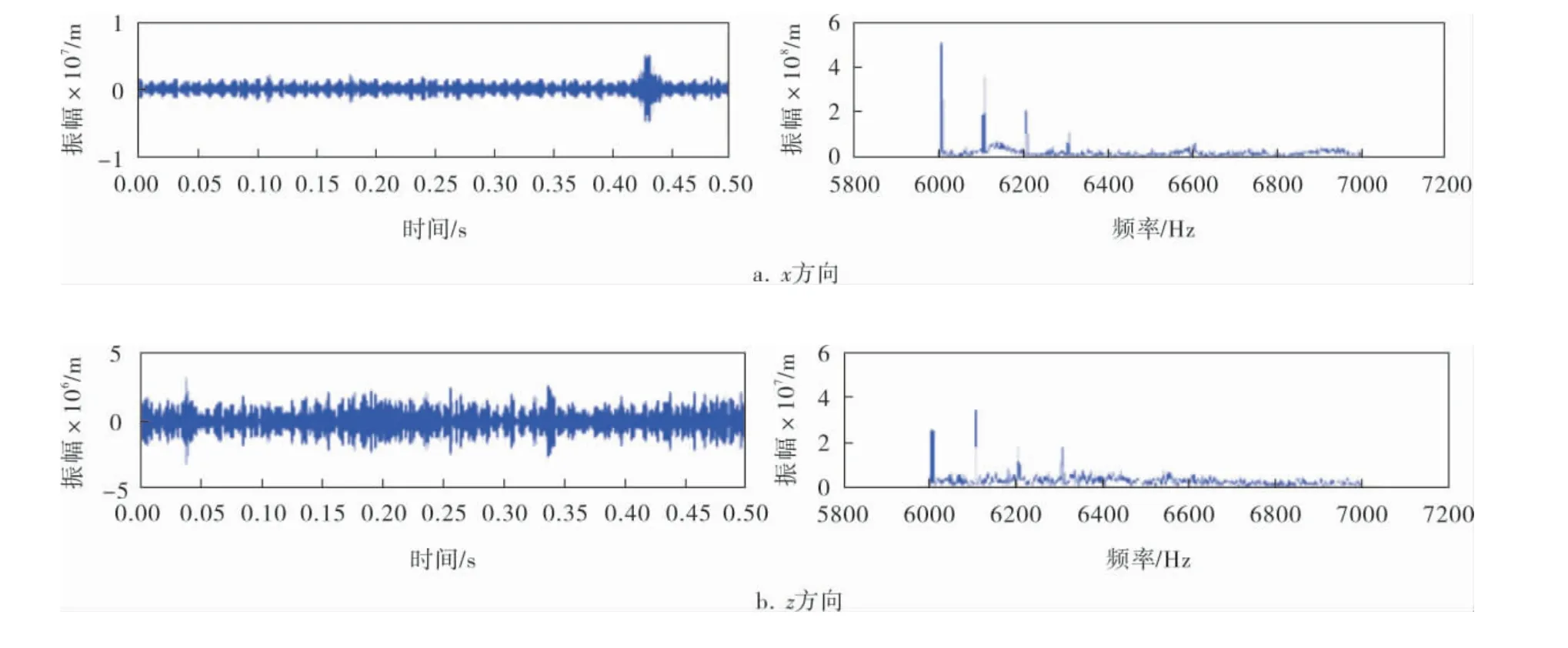
图7 转速400 r/min、载荷450 N时的实验测试时频域图

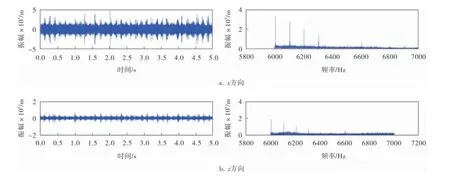
图8 转速600 r/min、载荷450 N时的实验测试时频域图

从图6～8可以看出，利用谐波小波包变换方法可以有效提取出实验测试中微弱的干气密封摩擦振动信号。相同工况下实验测试频率在6 000～6 800 Hz范围内变化时，实验测试振幅和理论模型计算振幅基本一致，同时在切向以10-8m量级变化，在法向以10-6m量级变化，这也验证了理论模型关于计算振幅的正确性。当载荷不变时，实验测试振幅随着转速的增大而增大，与理论模型计算振幅的变化趋势相一致。

3 对比分析与讨论

为了验证笔者所建理论模型的合理与正确，将上述工况下的理论模型计算结果与实验测试结果进行对比分析，结果如图9所示。可以看出，转速不变时，理论模型计算振幅与实验测试振幅在x、z方向上都随着载荷而变化。这是因为摩擦界面的摩擦振动实质上是通过动环与静环接触表面上的微凸体之间的相互作用产生的，当载荷发生变化时，势必会对动环与静环之间的真实接触面积、微凸体变形程度等实际接触状态造成改变而最终反映出振幅变化。同一工况下，理论模型计算振幅和实验测试振幅很接近，且理论模型的计算振幅普遍大于实验测试振幅，这是因为理论计算模型是在无阻尼下系统具有稳态解的前提下建立的，而实际实验测试则包含了阻尼等情况。通过对比分析可以得出，理论模型计算振幅与实验测试振幅虽然存在偏差，但两者的变化规律和趋势基本一致，摩擦振动振幅也在同一量 级，这进一步证明了笔者所建模型的合理与正确。

图9 不同转速下理论模型计算结果与实验测试结果对比

4 结论

4.1 基于分形理论构建了干气密封系统动环与静环端面间在干摩擦状态下考虑微观形貌与接触特性对宏观系统影响的两自由度滑动摩擦界面摩擦振动系统模型，并根据描述粗糙表面轮廓曲线的W-M函数，构建了包含分形参数的密封端面法向位移激励。

4.2 搭建了干气密封滑动摩擦界面摩擦振动实验测试平台，同时选用高精度加速度传感器、高速采集卡和LABVIEW信号采集系统对动环与静环端面间的摩擦振动信号进行实验测试。

4.3 采用谐波小波包变换分析和处理具有微弱特征的摩擦振动信号，结果表明，谐波小波包变换方法能够准确提取干气密封系统动环与静环端面间摩擦振动信号的特征信息。

4.4 载荷固定不变时，无论是理论模型得到的计算振幅还是实验测试的振幅都随着转速的增大而增大。当转速一定时，理论模型计算振幅与实验测试振幅均随着载荷的增大而增大。相同工况下，理论模型计算振幅和实验测试振幅的值接近，且理论模型的普遍大于实验测试的。对比分析得出，理论模型计算振幅与实验测试振幅虽然存在偏差，但两者的变化规律和趋势基本一致，摩擦振动振幅也在同一量级，这也进一步证明了笔者所建模型的合理与正确。