基于分数导数理论的横观各向同性饱和黏弹性地基中大直径嵌岩桩的竖向振动
2023-08-16李兴毓陈曦菲
李兴毓,陈曦菲
(1. 安徽省交通控股集团有限公司,安徽 合肥 230088; 2. 长沙理工大学 交通运输工程学院,湖南 长沙 410114)
0 引言
获得单、群桩振动特性以及饱和土-桩-上部结构体系动力响应的关键是研究饱和土-桩动力相互作用问题,这对饱和土中桩基的抗震、减振设计及完整性检测至关重要。近年来,越来越多的国内外学者对这一问题给予了广泛关注,已成为学术界和工程界的研究热点。回顾饱和土-桩动力相互作用的研究和发展历史,可以发现:现有的各向同性饱和土-桩基动力相互作用理论研究已经相当广泛和深入,所采用的模型和考虑的各种参数也很全面[1-12]。而相比之下,由于各向异性饱和土动力控制方程组较为复杂,数学处理上难度较大,而薄弱部分就体现在关于土骨架各向异性对桩基振动特性的影响研究。研究表明[13]:在实际工程中,由于自然沉降或固结,天然地基的扁平类介质颗粒表现出明显的排列方向,因此土体的水平和竖向性质往往存在较大差异,然而采用横观各向同性物理方程更能反映土骨架的实际力学特性。研究和准确反映对桩基动静态特性的影响,对于进一步提高桩基振动理论的实用价值具有重要意义。毫无疑问,考虑土骨架的横观各向同性,研究饱和地基与桩基的动力相互作用,在理论上和工程实践中都具有重要意义。
目前,基于现象学方法的Biot理论和基于混合理论的Boer多孔介质模型组成了描述饱和土宏观力学行为的主要理论。虽然Biot理论已成功应用于许多工程领域,但EDELMAN等[14]和BOER等[15-16]通过对比分析指出:Biot理论本质上是一种工程描述方法,并认为Biot动态控制方程中的质量平衡方程和动量平衡方程存在一定的局限性和不足。而Boer多孔介质模型相较于Biot理论其推导更为严格,且其基于连续介质混合物公理和体积分数概念,满足质量守恒定律与热动力学定律等物理公理[6,15-17]。如今,Boer多孔介质模型已发展到一个相对较高的水平,其在数学逻辑和物理本质上具有较好的一致性,可以满足理论的严密性和工程实践的各种要求[6]。
综上所述,本文将基于Boer建立的饱和多孔介质质量平衡方程和动量平衡方程,分别采用横观各向同性物理方程描述土骨架的实际力学特性,分数导数黏弹性本构方程描述土体的黏性,首先推导得到横观各向同性饱和黏弹性土体动力控制方程组,其形式为u-p形式。然后使用分离变量法求解该方程组得到桩侧土反力基本解,继而将桩基视为Rayleigh-Love杆处理的同时基于所得土反力建立横观各向同性饱和黏弹性土体中大直径黏弹性桩的竖向振动方程,继而求解该方程并结合桩土相容条件及边界条件推导得到桩顶竖向动力阻抗解析表达式,进而通过Fourier逆变换得到激振荷载为半正弦脉冲时的桩顶时域速度半解析解。最后在此基础上比较分析了土骨架的数值算例中黏性性质以及横观各向同性对桩基振动特性的影响。
1 数学模型
1.1 基于Boer多孔介质模型的横观各向同性饱和黏弹性土体动力控制方程组
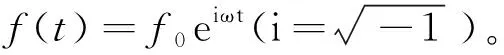

图1 横观各向同性饱和土大直径桩基的动力相互作用模型Fig. 1 Dynamic interaction model for a large-diameter pile in the transverse-isotropic saturated soil
1)土体表面为自由边界,无正应力和剪应力,表面具有渗透性,土和桩底部由刚性基岩支承。
2) 桩周围的土骨架是一种充满理想液体的横观各向同性饱和黏弹性材料。
3) 桩基为等截面黏弹性圆柱桩。
4) 桩土系统存在有小变形振动,在振动过程中二者保持密切接触,即接触面处桩土的位移和应力是连续的。
基于BOER等[15-16]建立的多孔介质模型,饱和土体的动量平衡方程和反映体积分数概念的质量平衡方程可表示为:
(1)
(2)
div(nSX′S+nLX′L)=0
(3)

(4)
式中:p为孔隙液相压力,Sv为表示土骨架和孔隙液体之间的耦合作用的液固耦合系数,含下标“E”的部分表示有效应力。此外,有:
式中:γLR为孔隙液体的真实比重,kL为土体Darcy渗透系数,u、v和w分别代表土体的径向(r)、环向(θ)和竖向(z)的位移分量。字母S、P和L分别表示土骨架、桩和孔隙流体。
根据图1所示桩土体系的受力和几何条件可知:桩土体系符合轴对称条件。对于土体的黏弹性,目前已有很多描述模型,比如粘滞阻尼模型和分数导数模型等。而根据已有研究可知[6,13,18]:分数导数粘弹性模型具有精确度高,确定模型所需的试验参数少,应用范围广的优点。为此,本文采用分数导数粘弹性本构描述土骨架应力应变关系,具体可表示为:
(5)
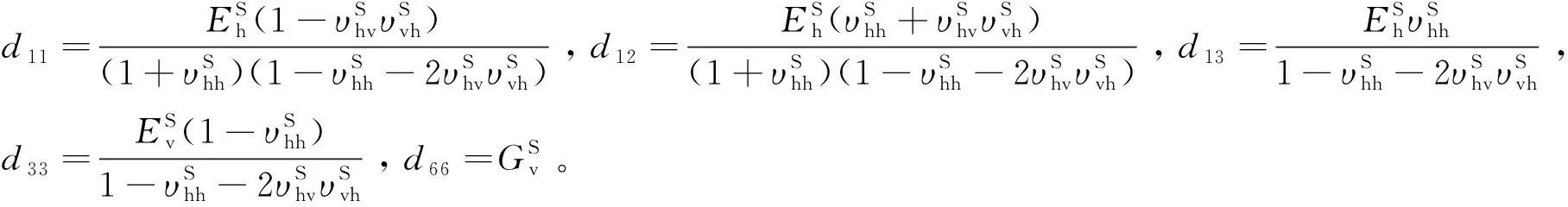
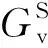
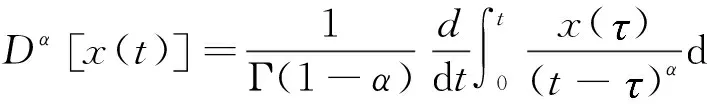
(6)

土骨架几何方程为:
(7)
(8)
(9)
(10)
(11)
(12)
1.2 桩侧土反力基本解求解
由于直接求解式(8)-式(12)有很大的难度,并且无法得到问题的解析解。而YU等[5]、刘林超[6]、CAI等[22-23]、NOGAMI等[20]和NOVAK[21]已通过且研究结果表明:土体的径向位移对桩-土体系的竖向振动影响不大。有鉴于此,本文忽略土的径向位移的影响,而只考虑土体的竖向波动效应,即令uS=uL=0,可将式(8)-式(12)进一步简化为:
(13)
(14)
(15)

(16)
(17)
(18)
将上述无量纲量代入式(16)-式(18)中可得到:
(19)
(20)
(21)
桩-土系统满足以下无量纲边界条件:
在无穷远处,位移衰减为零,即:
(22)
在土体表面处正应力为零,即:
(23)
地基土底面为刚性基岩支承,即:
(24)
在桩土接触面处位移连续,即:
(25)
联立式(19)和式(20)可得:
(26)
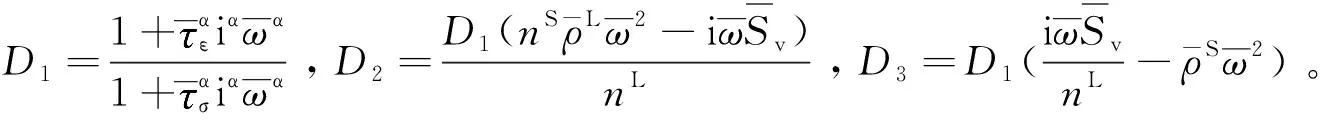
由式(21)可得:
(27)

(28)

(29)
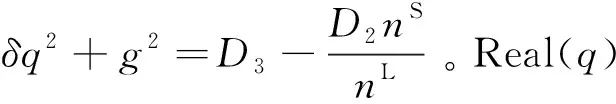
求解式(29)可得:
(30)
即:
(31)
将其代入式(5)、式(7)、式(22)和式(23)中可推得B=0,C+D=0,D=-C,AC=A1。
故
(32)
在求解式(32)并考虑无限远边界条件式(22)后,可以得到:
(33)
将式(33)代入边界条件式(24)中可得:
(34)
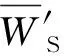
(35)
则由式(5)和式(7)可得:
(36)
1.3 桩顶动力阻抗及速度时域响应求解
基于图1所示的动力相互作用模型,将桩基础视为Rayleigh-Love杆[24],通过将上述桩侧土反力基本解结合起来,从而建立横观各向同性饱和黏弹性土中大直径黏弹性桩基的振动控制方程,如下所示:
(37)
桩基内力为:
(38)
将式(38)无量纲化为:
(39)
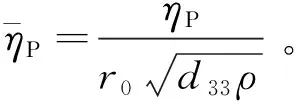
将桩基方程式(37)无量纲化为:
(40)
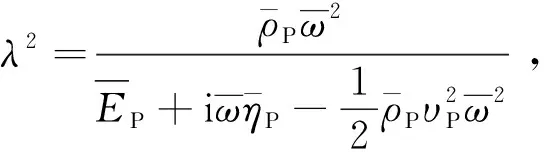
式(40)的齐次方程通解为:
(41)
式(40)的特解可设为:
(42)
将其代入桩基振动方程式(40)中,可以得出:
(43)
则桩基振动方程式(40)的解为:
(44)
将式(35)和式(44)代入桩土体系的连续性条件式(25)中可得:
(45)
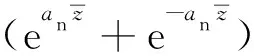
(46)
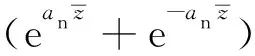
An=X1na1+X2na2
(47)
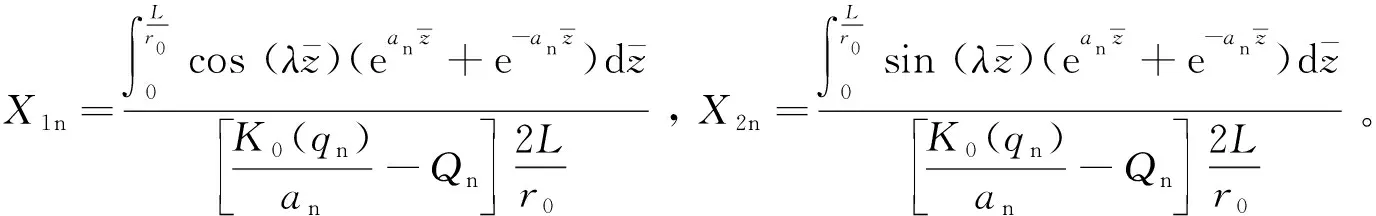
则:
(48)
桩基满足如下无量纲边界条件:
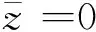
(49)
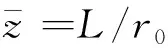
(50)
将式(48)代入式(49)和式(50)中可推得:
(51)

定义桩顶动力阻抗为:
(52)
将其无量纲化为:
(53)
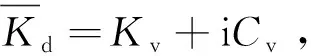
桩顶速度频域响应为:
(54)

图2 脉冲作用力Fig. 2 Pulse force
(55)
将其无量纲化为:
(56)

2 数值算例分析
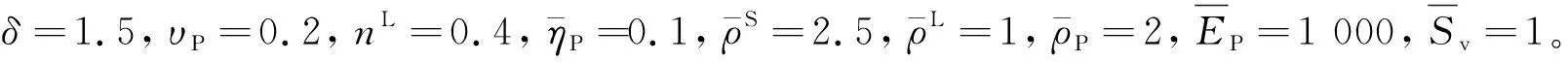
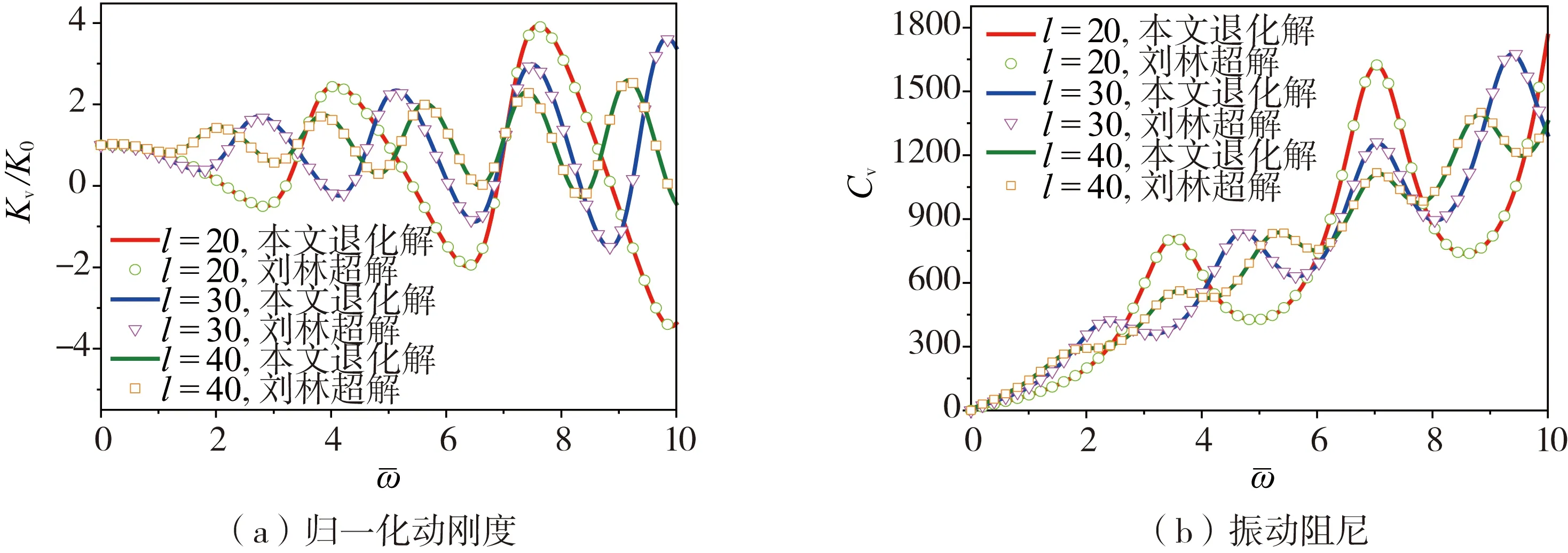
图3 本文退化解与刘林超[6]解对比情况Fig. 3 Present reduced solution versus Liu's results[6]
2.1 解的验证与比较
另一方面,利用ADINA软件建立桩-土体系的轴对称有限元模型,如图4所示。图5为本解与有限元法计算桩身位移和桩顶速度的结果对比。在该有限元模型中,采用多孔材料的9节点矩形单元模拟土体;将模型左侧设为轴对称边界,土体表面设为自由边界,底部设为不透水固定边界,右侧设为零孔压固定边界,模拟无限远边界条件,与图1中规定的边界条件保持一致。需要注意的是:取模型宽度50 m足以得到本例的稳态响应振幅,已经能够消除右侧的边界效应。从图3-5的对比可以看出:本文提出的解与已有研究研究和有限元计算结果吻合良好,验证了本文的正确性。

图4 基于ADINA的桩-土系统轴对称有限元模型Fig. 4 Axisymmetric finite element model with ADINA for the pile-soil system
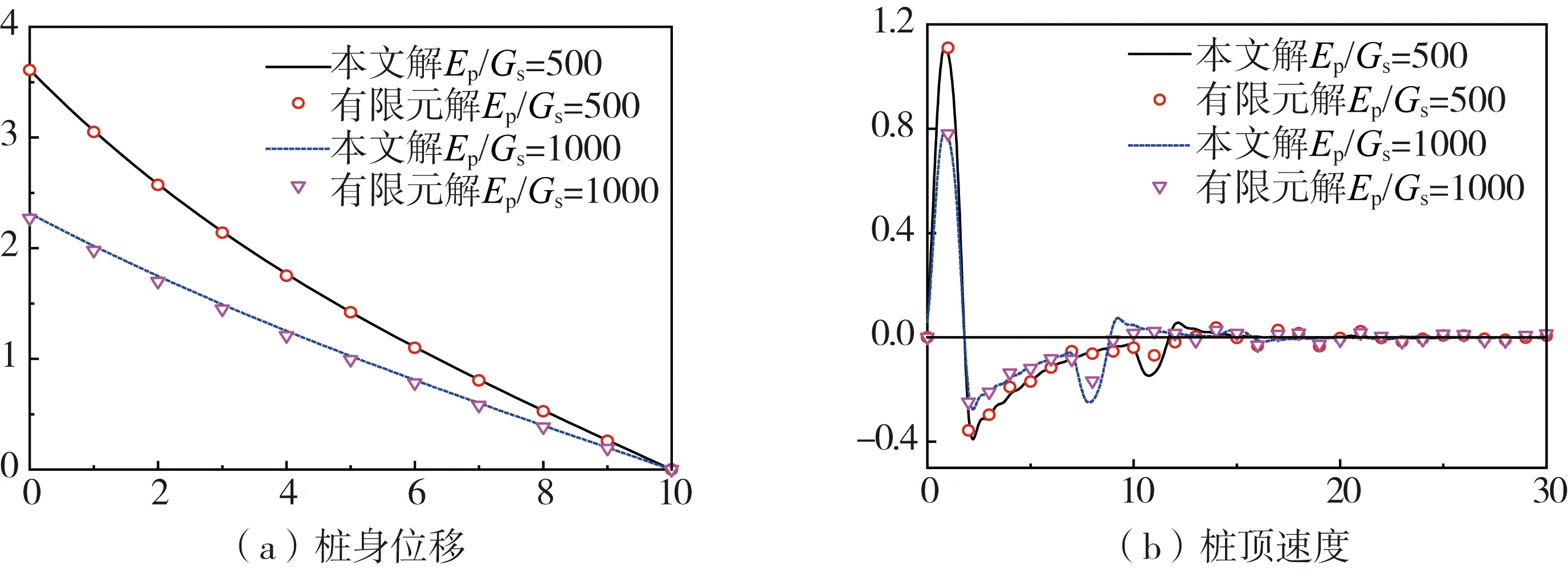
图5 饱和土-桩相互作用系统有限元分析结果与本文解的比较Fig. 5 Comparisons of the present results with FEM (ADINA) results for the interaction system of saturated soil and pile
2.2 桩基振动特性参数化分析
桩顶的动力特性受土体横观各向同性特性的影响如图6所示。从图中可见:桩顶动力阻抗曲线的共振频率基本上不受土体各向异性影响,而对其桩顶速度响应以及共振峰值则有显著影响。随着表示土体的横观各向同性特性差异的参数δ的增加(意味着d66更大),桩顶动刚度和阻尼的共振峰值均随之显著减小。此外,桩顶速度响应的反射波幅值亦随之显著减小,当δ较大时,相应的多次反射波信号已经消失。显然,这不利于桩基的检测工作。
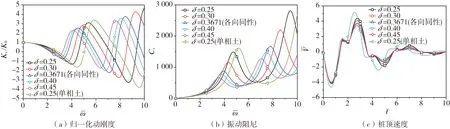
图6 土体各向异性对桩顶阻抗和速度响应的影响Fig. 6 Influence of the soil's anisotropy on the pile top's impedance and velocity

图7 桩顶阻抗和速度响应随不同土体粘滞特性的变化情况Fig. 7 Pile top’s impedance and velocity with different soil viscosity
分数导数的阶数对桩顶动力特性的影响如图8所示。从图中可以看出:随着分数导数模型阶数α的增加,桩顶动力阻抗的共振频率随之略有增加,相应的共振幅值随之大幅增加,特别是在高频阶段犹为显著。另外,桩顶时域速度曲线的反射波信号幅值亦随之明显增大,然从整体来看:其变化幅度相对较小。
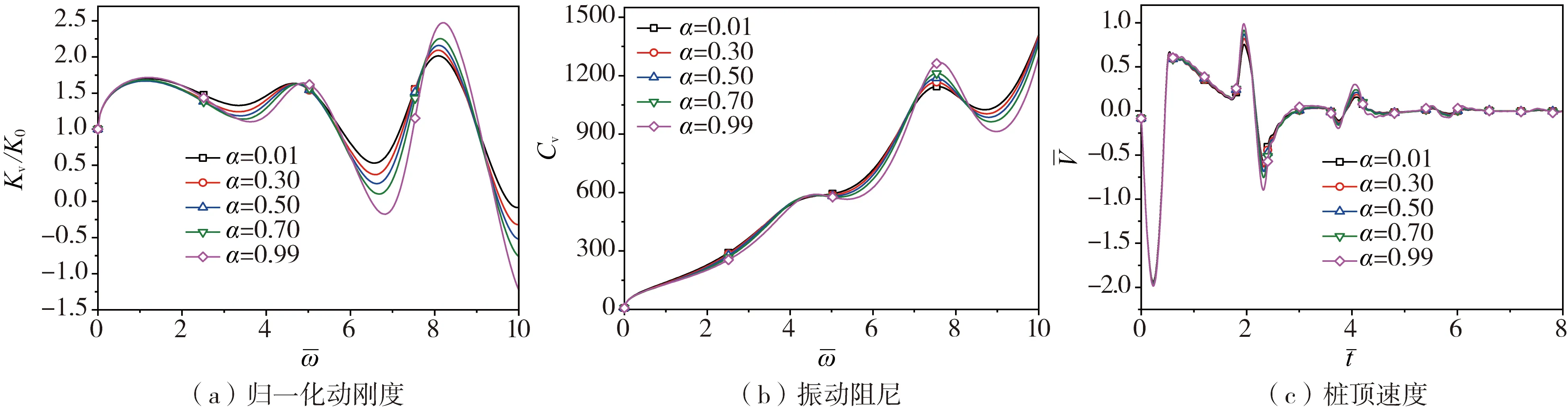
图8 桩顶阻抗和速度响应随不同分数阶导数的变化情况Fig. 8 Pile top’s impedance and velocity with different fractional derivative orders
土体渗透系数对桩-土系统动力特性的影响如图9所示。从图中可以看出:随着土体渗透系数的减小,桩-土系统的动力阻抗和反射信号强度逐渐减小,最终不再发生变化。这是因为与单相土相比,饱和土是一个耗散体系,其耗散能力相当于阻尼系数,随着土体渗透性的降低而增大。当渗透系数很小时,土体不排水,不再随渗透系数的变化而变化。
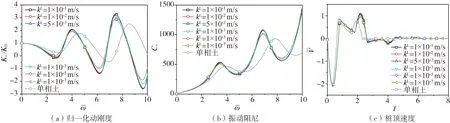
图9 土体渗透系数对桩-土系统动力特性的影响Fig. 9 Effects of the soil permeability on the dynamic characteristic of the pile-soil system
3 结论
本文基于Boer建立的饱和多孔介质质量平衡方程和动量平衡方程,考虑土骨架的横观各向同性和黏性特性,首先推导得到横观各向同性饱和黏弹性土体动力控制方程组,其形式为u-p形式,然后采用分离变量法求解该方程组得到桩侧土反力基本解,根据所得桩侧土反力,同时将桩基视为Rayleigh-Love杆处理建立了大直径黏弹性桩基在土中的竖向振动方程,然后结合桩土协调条件和边界条件求解振动方程,推导出桩顶竖向动力阻抗的解析表达式,最后通过Fourier逆变换得到了激振荷载为半正弦脉冲时桩顶速度的时域半解析解。在解退化后,通过与现有研究的比较,验证了本文建立的模型的正确性。基于此,通过数值算例比较分析了土体黏性参数、土体横观各向同性参数和分数导数阶数对桩基振动特性的影响,得出了一些有意义的结论。计算分析表明:
1) 通过将本文所建立模型的退化结果和已有研究的对比分析验证了本文推导的合理性。各向同性土解可视为本文解的特殊情况。显然,对于一些尚未建立模型的相关实际情况,通过适当变化参数,可方便地利用本文解来进行退化分析。
3) 随着土体渗透系数的减小,桩顶动力阻抗和速度响应随之减小。当土体渗透系数很小时,在动荷载作用下土体将产生不排水现象,此时渗透系数对桩基振动特性的影响可忽略不计。
