基于多尺度模型的空间Y型拱桥抗震性能分析
2023-08-18王朝进吴睿麒高鑫崇王利辉
韩 强,王朝进,吴睿麒,高鑫崇,许 坤,王利辉
(1. 北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124; 2. 北京市市政工程设计研究总院有限公司,北京 100082;3. 北京市城市桥梁安全保障工程技术研究中心,北京 100082 )
0 引 言
近年来,异型拱桥由于其美观性被广泛应用于城市建设,同时因其桥型空间结构上的独特性,使得结构体系受力非常复杂,空间效应突出,桥梁设计极具挑战性。特别是建在高震区大跨度异形桥梁,地震安全风险高[1-3],超出现行桥梁抗震设计规定范围。大跨度异型拱桥抗震安全性受到桥梁工程师和工程抗震研究人员重点关注。
目前,在桥梁结构的抗震分析中,通常采用梁单元对整个桥梁进行建模分析,即建立桥梁“脊骨梁”模型[4]。这种方法能够得出桥梁整体动力特性、内力及应力分布。这种建模方法将一个复杂截面简化为一个点,大大提高了计算效率,然而无法获得桥梁某些关键部位的局部动力效应、应力集中、疲劳和断裂等情况[5]。同时,由于大跨度桥梁结构复杂和体量巨大,如果根据结构实际情况进行全尺度精细化模拟(如采用实体单元或板壳单元),所建有限元模型的规模将非常庞大,这对计算设备的计算容量、计算能力以及分析软件都有很高的要求,这些要求在现阶段都难以实现[6]。因此,作为一种平衡精度和计算代价的有效途径,多尺度仿真分析已逐步成为大跨度桥梁性能分析和评估的主流选择[7-9]。许多研究人员对多尺度连接方法进行了探索和研究[10-15],多尺度仿真分析核心是通过采用不同尺度的单元对大跨度桥梁进行模拟计算,即对桥梁整体采用宏观模型(梁单元模型),对桥梁设计和受力较为复杂的局部关键部件建立微观精细模型(板壳单元或实体单元模型),通过采用不同单元之间合理的连接方式使得宏观模型与微观模型协同计算,更准确高效的得出桥梁整体与局部构件受力情况。
本文以一座特大跨径空间Y型拱梁组合体系桥为工程背景,基于多尺度建模技术,建立了该桥多尺度有限元模型,并通过与杆系模型对比,验证了多尺度建模方法的精确性与可靠性。采用时程分析法计算分析了大跨度空间Y型拱桥结构整体和局部关键部件的地震响应,对其抗震性能进行合理评估
1 多尺度建模方法
多尺度建模方法是通过不同类型和尺度的单元模拟结构不同部位以保证计算精度和效率的方法。不同尺度单元界面处的连接应确保在不损失宏观模型自由度的同时,尽可能不增加微观模型的额外约束[16]。目前,工程结构中主要涉及三种单元连接方式:梁单元-实体单元连接、梁单元-壳单元连接和壳单元-实体单元连接。事实上,不同单元之间的连接原理基本相同,本文将以梁单元模型与壳单元模型的连接来说明不同单元的连接原理。
本文通过ABAQUS有限元软件,采用耦合连接(Coupling)命令中的动力耦合(Kinematic Coupling)方式连接梁单元模型与壳单元模型[17],如图1所示,以梁单元节点为主节点,壳单元上所有节点为从节点,通过耦合的方法将壳单元上所有节点的六个自由度均进行约束,梁单元节点与壳单元面上节点之间的距离保持不变,同时壳单元各个节点之间的相对距离保持不变,保证梁单元节点与板壳单元节点之间的位移协调[18]。
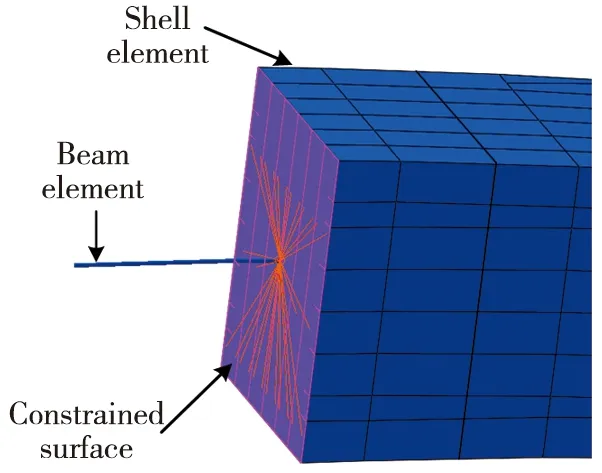
图1 耦合面三维示意图
假定初始时刻位于交界面的梁单元节点A与交界面壳单元节点Bn坐标分别为A(0,0,0)与Bn(xn,yn,zn),梁单元节点有三个平动自由度和三个转动自由度,而板壳单元节点仅有三个平动自由度,如图2所示,因此,基于平截面假定可得到梁单元节点位移向量A(ux0,uy0,uz0,θx0,θy0,θz0)与板壳单元节点位移向量为Bn(uxn,uyn,uzn)的控制方程如下:
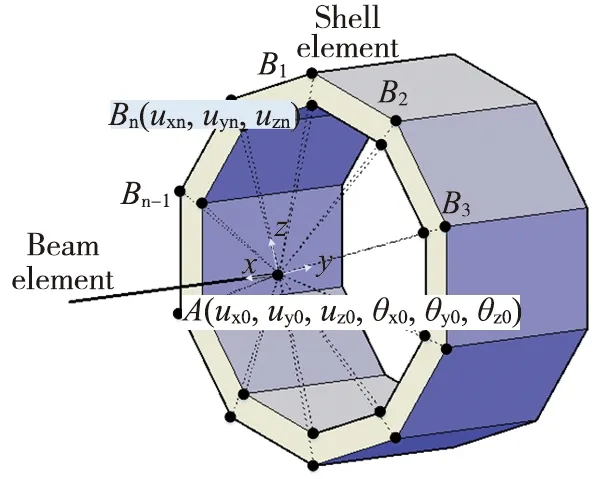
图2 耦合面节点位移协调示意图
uxn=ux0+yn·θz0+zn·θy0
(1)
uyn=uy0+zn·θx0+xn·θz0
(2)
uzn=uz0+xn·θy0+yn·θx0
(3)
式中:xn、yn和zn为壳单元节点相对于梁单元节点A的坐标,ux0,uy0,uz0和θx0,θy0,θz0分别为梁单元A的平动位移和转角。
2 多尺度建模实例
2.1 工程背景
图3为廊坊市某空间Y型拱桥示意图,该桥主桥全长256 m,跨径为35 m+164.5 m+56.5 m,上部结构由钢主梁、斜吊杆及Y型拱肋三部分组成,抗震基本设防烈度VIII度。主梁采用南北两幅分离式钢箱梁,两幅之间采用横梁进行连接;吊杆采用扇形斜向布置,主梁上吊杆间距9 m,全桥共有吊杆12对,合计24根;拱肋采用空间“Y”型变截面箱形钢拱肋,拱肋侧面上下缘投影线为不共焦点的椭圆线,空间Y型拱肋的一端在中央隔离带处与主梁横梁连接,下接中墩支座;拱肋在拱顶处进行分叉,将单拱肋分叉为双拱肋,分叉处轴线夹角为11.768°;分叉后的双拱肋分布于主梁两侧,通过拱脚的拱梁结合部与主梁连接。分叉后拱肋通过横撑保证其抗侧移性能。主梁和钢拱肋采用Q420钢材,分叉后拱脚拱梁结合部分内部灌入混凝土采用C40混凝土,桥梁盖梁和桩基等采用C30混凝土。
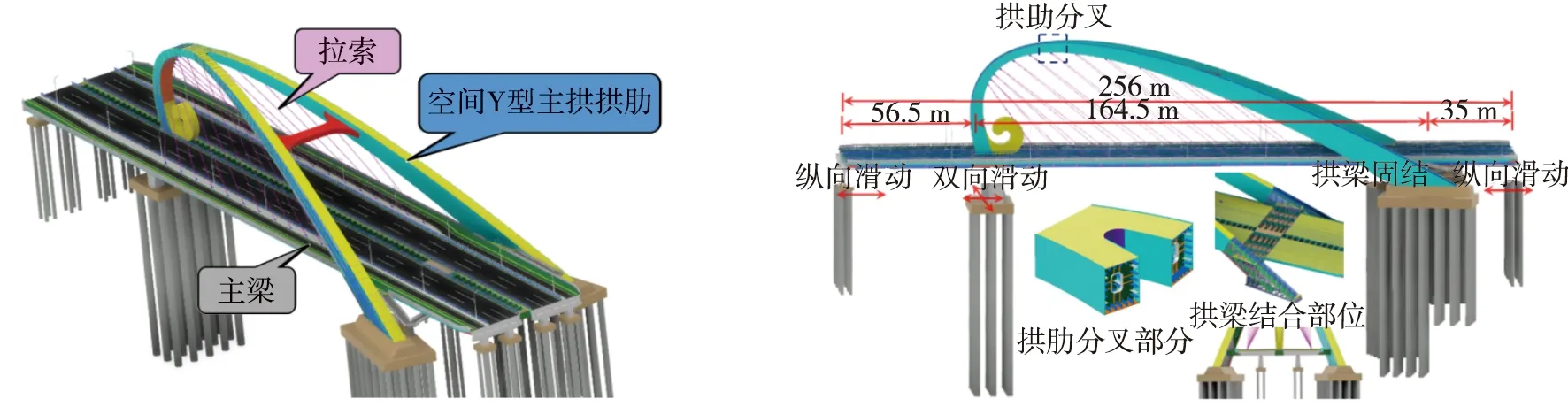
图3 空间Y型拱桥示意图Fig. 3 Schematic diagram of space Y-shaped arch bridge
2.2 多尺度有限元模型
全桥多尺度模型由精细模型与杆系模型两部分组成。桥梁拱梁结合部位和拱肋分叉部位为该空间Y型拱桥结构设计上的难点和要点,结构形式复杂,传统的杆系模型不能很好的模拟其结构力学特性,因此,对该部分进行精细化建模;主梁和拱肋等其余部分采用传统杆系建模方法进行模拟如图4所示。全桥多尺度模型共建立了326243个节点,11 831个梁单元,310655个板壳单元,24个桁架单元,1903个实体单元。
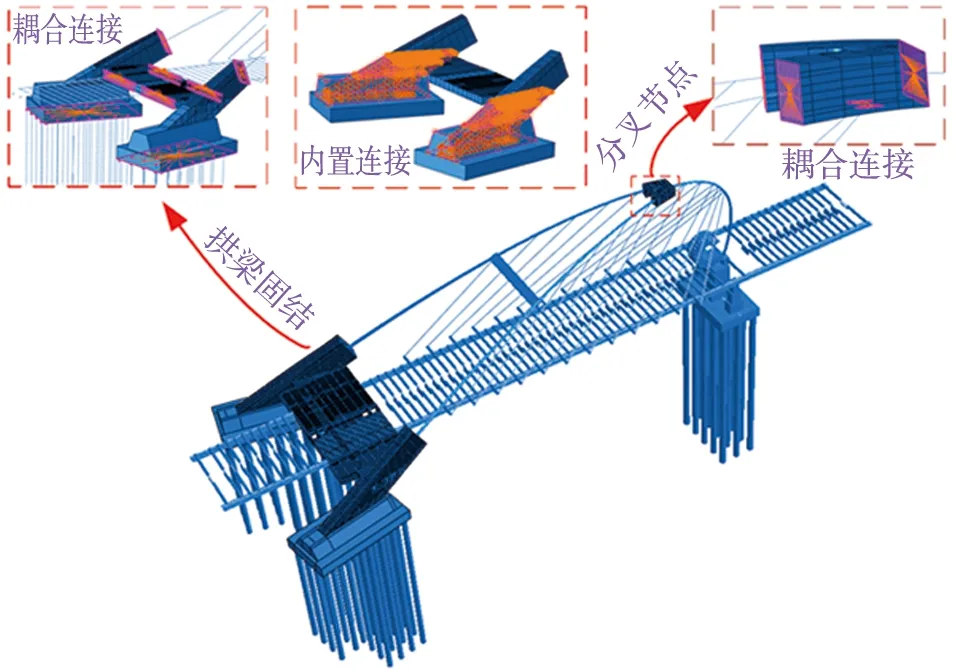
图4 桥梁多尺度模型Fig. 4 Bridge multi-scale model

图5 拱梁结合部位精细模型Fig. 5 Fine model of arch-beam joint

图6 拱肋分叉部位精细模型Fig. 6 Fine model of the bifurcation of the arch rib
桥梁拱梁结合部位和拱肋分叉部位钢箱室部分采用三维板壳单元S4R进行建模,桥梁拱梁结合部位内部灌入混凝土及与其相连的承台采用三维板实体单元C3D8R进行模拟如图5-6所示。主梁和拱肋等其余部分采用梁单元B31模拟,吊杆采用桁架单元T3D2模拟。吊杆与主梁之间采用刚臂进行连接;支座采用弹簧-阻尼单元(Springs/Dashpots)进行模拟;桩土作用采用M法等效土弹簧进行计算,采用Bushing连接单元模拟;桥梁拱梁结合部位钢拱肋部分与内部灌入混凝土及拱梁结合部位相连的承台之间的接触关系均采用内置区域(Embedded Region)方式进行模拟,忽略钢板与混凝土之间的粘结滑移。基于上文提出的多尺度耦合连接方法,进行桥梁精细模型与杆系模型连接,保证结构不同尺度连接界面之间变形协调,同时考虑到杆系元与板壳单元连接处截面进行了刚化处理,为保证模拟准确性,Y型分叉处模拟长度取该节段设计长度两端各延伸一米的总长度。
2.3 杆系模型
为验证上述多尺度模型准确性,建立了相同参数下的杆系模型,即全桥均采用梁单元和桁架单元模拟。与多尺度模型不同的是:拱梁结合部位拱肋与主梁大横梁之间采用绑定约束(Tie),拱肋单拱段与双拱段采用刚臂进行连接,如图7所示。全桥共建立了12488个节点,35917个梁单元,24个桁架单元。
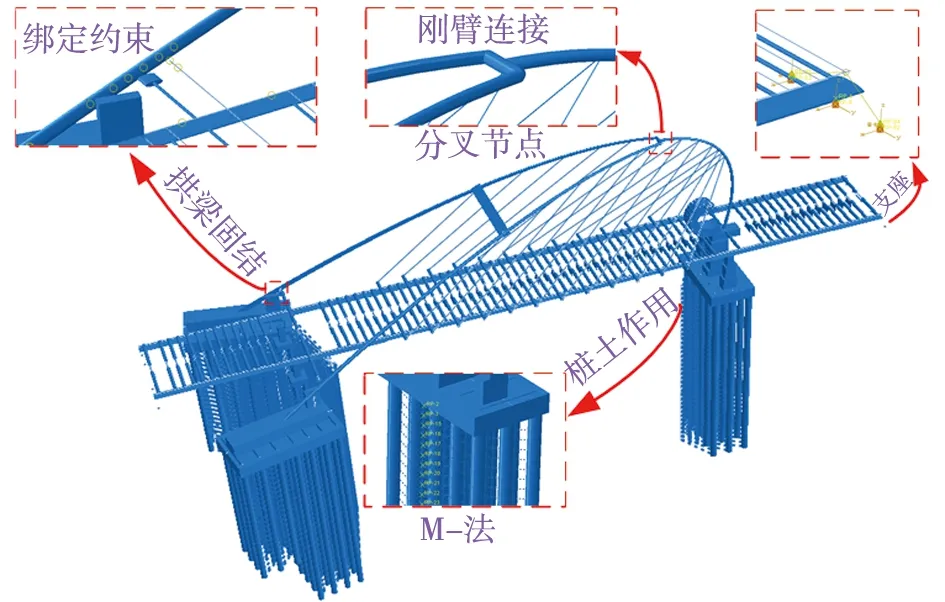
图7 全桥杆系模型Fig. 7 Full bridge rod system model
2.4 空间Y型拱桥动力特性对比
桥梁的动力特性是指对桥梁自振动频率和主振类型进行计算分析,是桥梁结构地震研究的基础。本文针对空间Y型拱桥杆系模型和多尺度模型进行了动力特性分析,结果见表1,桥梁杆系模型与多尺度模型前五阶振型形状如图8所示。大跨Y型拱桥低阶振型主要以受弯为主。多尺度模型和杆系模型同阶振型频率误差不超过5%,两种模型桥梁振型特点基本一致。总体来看:桥梁多尺度模型的动力特性与杆系模型相比并无明显差异,表明此多尺度连接方法可以有效实现不同尺度模型之间的变形协调。

图8 桥梁两种模型前五阶振型形状Fig. 8 Shapes of the first five vibration modes of the two bridge models
3 空间Y型拱桥地震响应
3.1 地震波选取
本文采用时程分析法对空间Y型拱桥进行地震响应分析。对于时程分析来说,合理的选择地震波对结构地震响应分析是非常关键的。本文中选取地安评报告提供的三条安评地震波(如图9)进行桥梁地震动响应分析。地震波输入方向考虑纵向、横向、纵向+竖向和横向+竖向四种组合,共计12种地震荷载工况,其中:工况1~3(H1X~H3X)为纵向加载,工况4~6(H1Y~H3Y)为横向加载,工况7~9(V1XZ~V3XZ)为纵向与竖向加载,工况10~12(V1YZ~V3YZ)为横向与竖向加载。
3.2 主梁地震响应
地震作用下,空间Y型拱桥主梁由于斜吊杆的水平分力作用,主梁变形和内力最大处并未出现在主梁跨中等桥梁对称位置,而是根据位移和内力响应的不同,最大响对应位置也发生改变。因此,根据主梁与吊杆的位置分布设立了观测点,如图10所示。
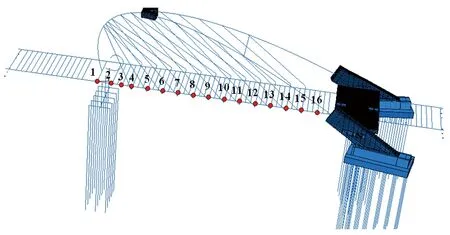
图10 主梁观测点Fig. 10 Observation point of main beam
对桥梁多尺度模型进行地震响应分析,主梁位移与内力峰值响应见表2,主梁最大位移与内力时程响应如图11所示。地震作用下,主梁纵向位移最大处位于主梁1号观测点处,在工况2时主梁纵向位移最大,最大值为-6.1 cm;主梁横向位移最大处位于主梁6号观测点处,在工况6时主梁横向位移最大,最大值为18.4 cm;主梁竖向位移最大处位于主梁11号观测点处,在工况9时拱肋竖向位移最大,最大值为-25.1 cm。地震作用下,主梁轴力最大处位于主梁16号观测点处,在工况2时主梁轴力最大,最大值为64777.5 kN;主梁弯矩最大处位于主梁2号观测点处,在工况7时主梁弯矩最大,最大值为148837.0 kN·m;主梁应力最大处位于主梁2号观测点处,在工况11时主梁应力最大,最大值为233.2 MPa。在单向和双向组合地震动荷载作用下,主梁的竖向位移最大,横向位移次之,纵向位移最小。这说明在地震作用下,该异形拱桥结构以主梁竖弯振型为主,这与地震作用下结构以低阶振型响应为主的规律一致。
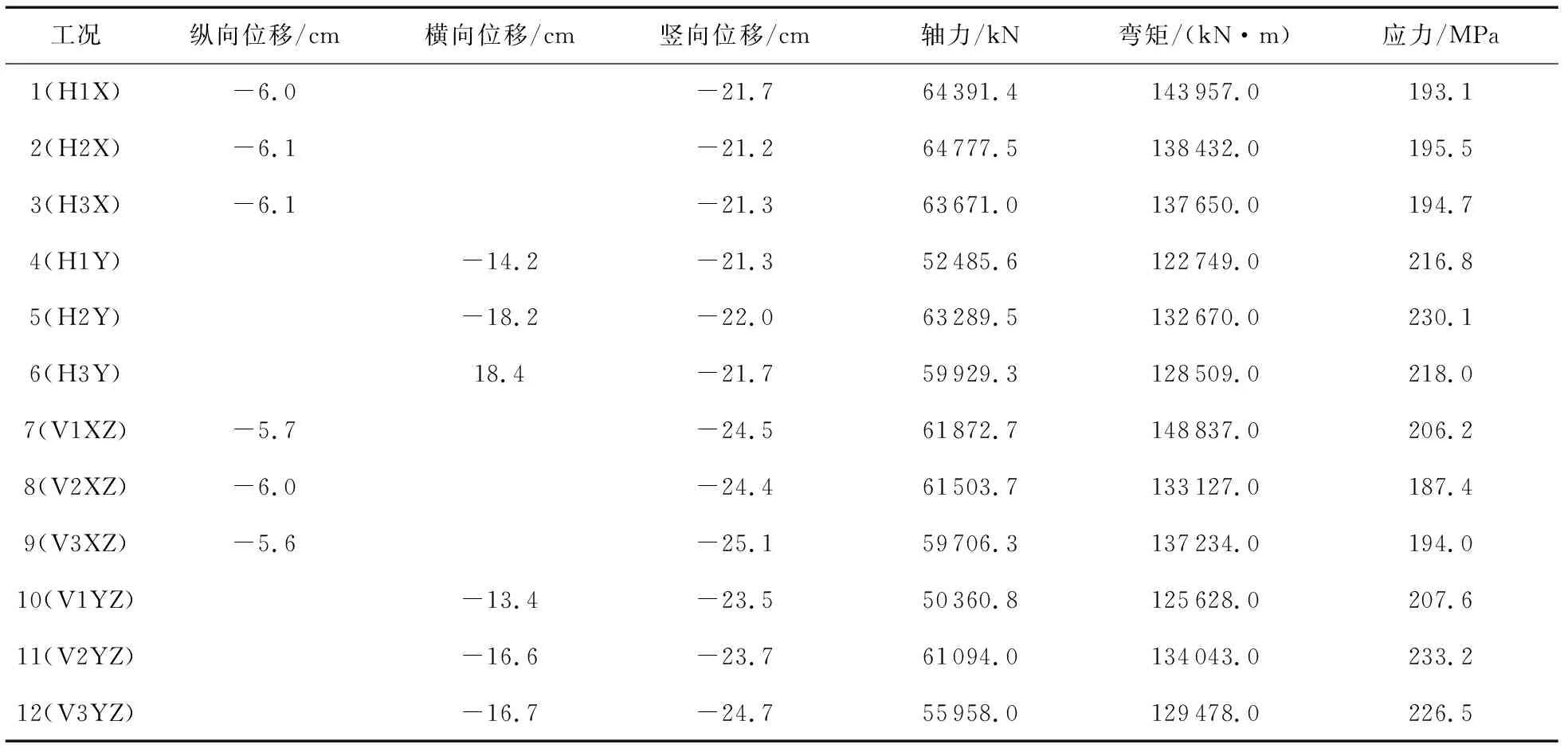
表2 地震作用下桥梁主梁位移与内力峰值响应Table 2 Displacement and peak internal force response of bridge girder under earthquake
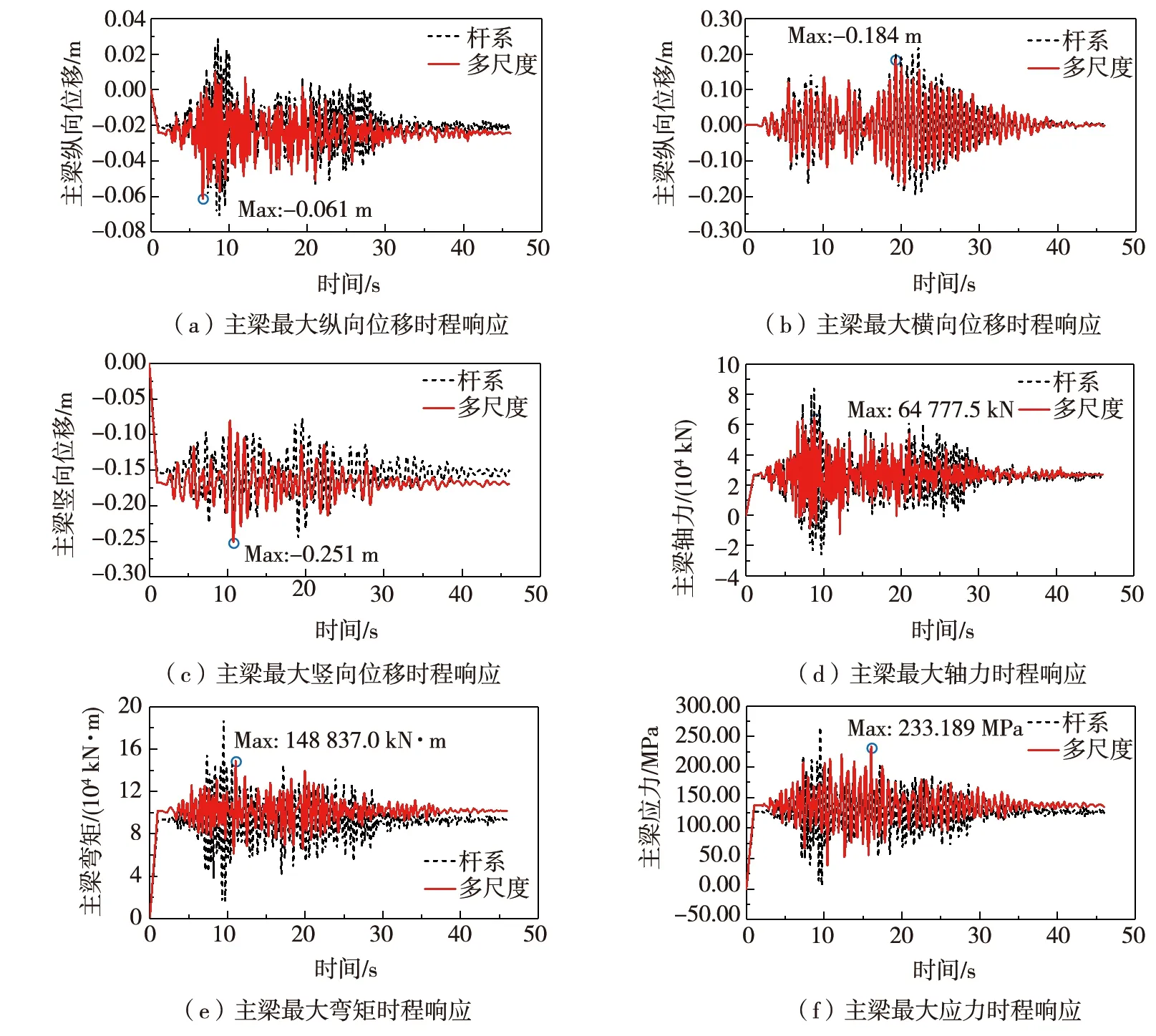
图11 地震作用下主梁最大位移与内力时程响应Fig. 11 Time-history response of maximum displacement and internal force of main girder under earthquake
由图11可以看出:桥梁杆系模型和多尺度模型主梁最大地震动时程响应曲线具有一定的相似性,说明了多尺度模型能很好地反映桥梁主梁地震响应特征。不同的是:与杆系模型相比,多尺度模型桥梁主梁地震响应幅值相对较小,可能的原因是:桥梁多尺度模型将拱梁结合部位和拱肋分叉部位中的横隔板以及加劲肋等细节部件进行精细化建模,对桥梁结构刚度模拟更为精确。
3.3 拱肋地震响应
与一般拱桥不同,由于空间Y型拱肋的横向不对称性以及斜吊杆水平分力的存在,拱肋不仅承担较大轴向压力,还要承担部分的弯矩作用,导致拱肋分叉前单拱段拱肋与分叉后双拱段拱肋的受力状态存在巨大差异。由于该空间Y形拱桥关于顺桥向对称,在进行拱肋地震响应分析时仅列出拱肋单拱段和一侧双拱段的计算结果,拱肋观测点位如图12所示。
地震作用下拱肋位移与内力峰值见表3,拱肋最大位移与内力时程响应如图13所示。地震作用下,拱肋纵向位移最大处位于单拱段4号观测点处,在工况7时拱肋纵向位移最大,最大值为-17.5 cm;拱肋横向位移最大处位于双拱段14号观测点处,在工况5时拱肋横向位移最大,最大值为45.8 cm;拱肋竖向位移最大处位于双拱段13号观测点处,在工况9时拱肋竖向位移最大,最大值为37.1 cm。地震作用下,拱肋轴力最大处位于双拱段18号观测点处,在工况5时拱肋轴力最大,最大值为56850.3 kN;拱肋弯矩最大处位于单拱段3号观测点处,在工况7时拱肋弯矩最大,最大值为-227809.0 kN·m;拱肋应力最大处位于单拱段3号观测点处,在工况7时拱肋应力最大,最大值为184.4 MPa。
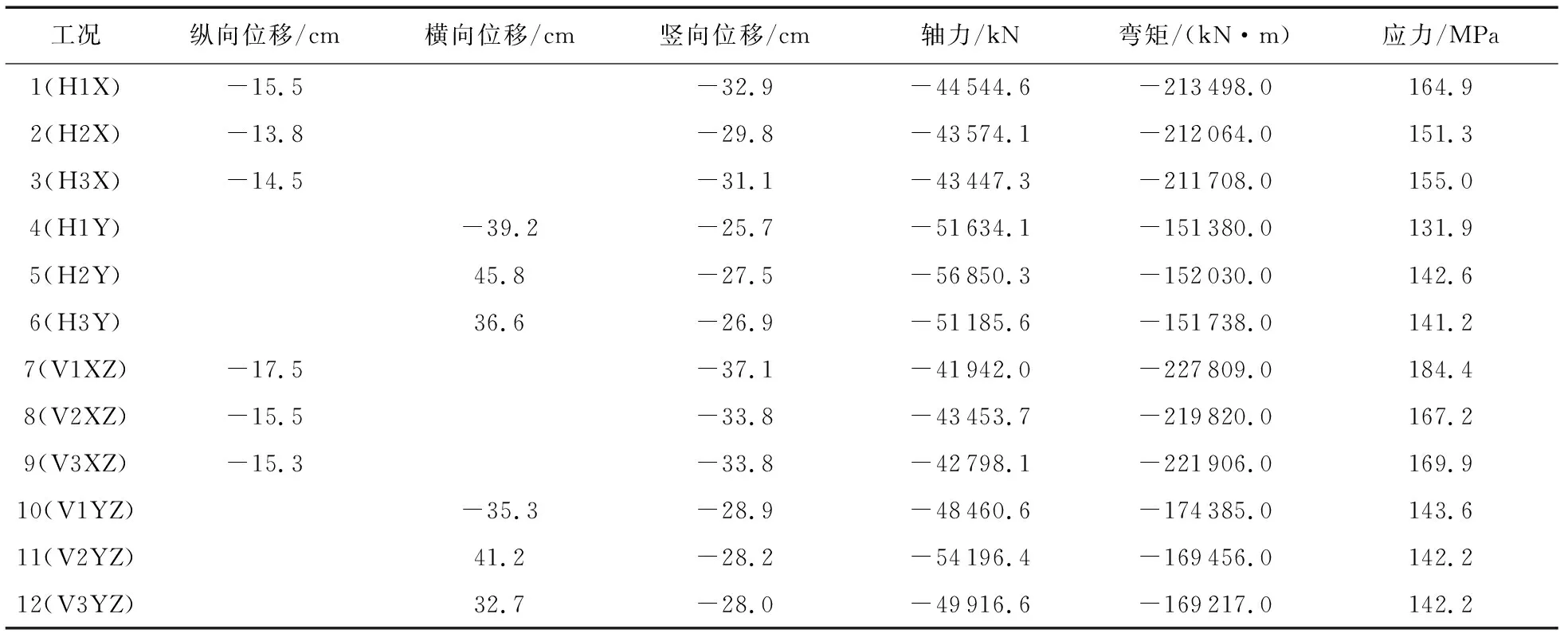
表3 地震作用下桥梁拱肋位移与内力峰值响应Table 3 Displacement and peak internal force response of bridge arch rib under earthquake
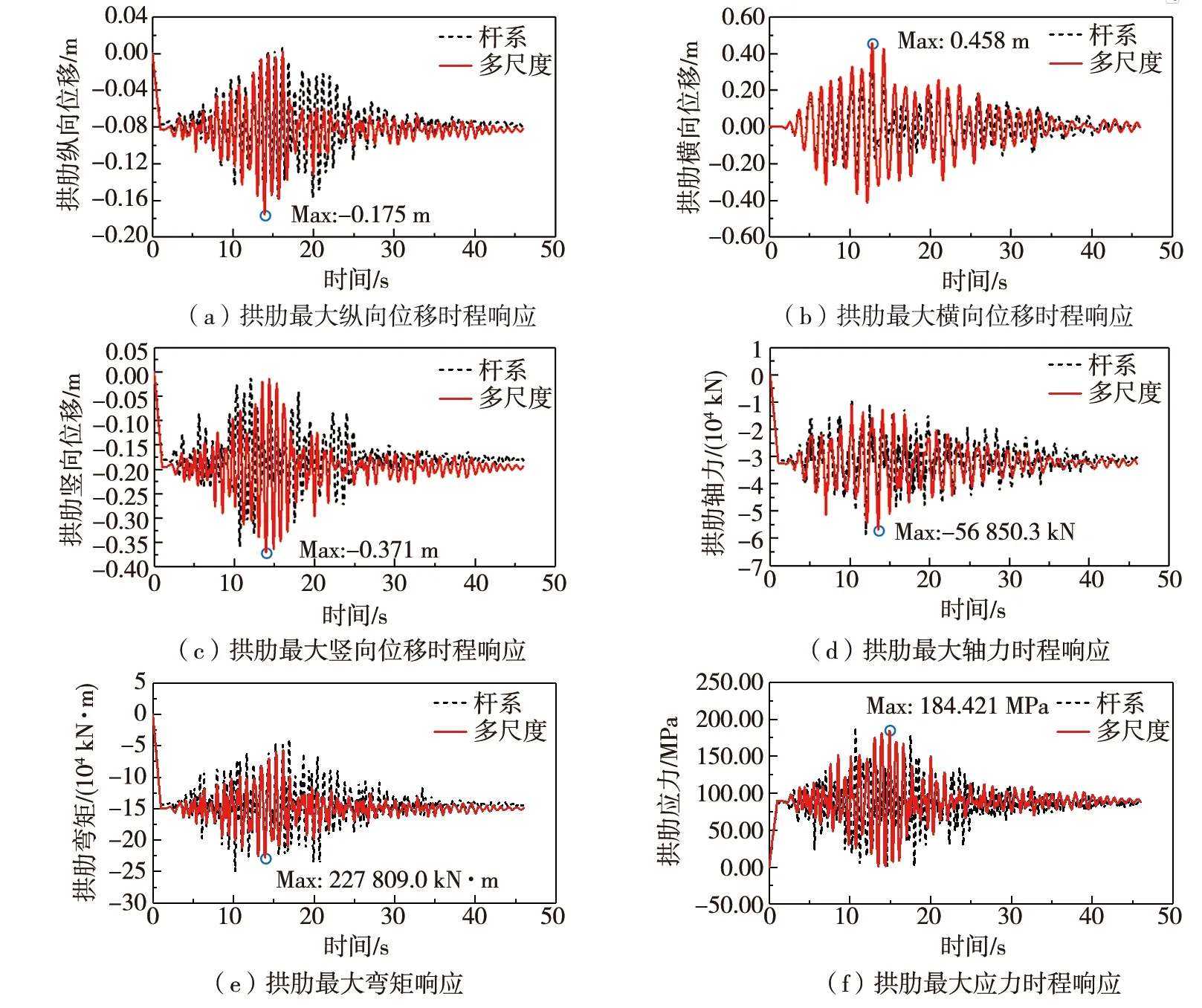
图13 地震作用下拱肋最大位移与内力时程响应Fig. 13 Time history response of arch rib maximum displacement and internal force under earthquake
综上所述,地震作用下,空间Y型拱桥拱肋主要变形发生在单拱段4号观测点、双拱段13号及双拱段14号观测点处,且拱肋横向位移最大,竖向位移次之,纵向位移最小,这与桥梁低阶振型拱肋横向侧弯与竖向变形特点一致,同时也暴露出该桥梁拱肋横向与竖向刚度,尤其是拱肋横向刚度较为薄弱,在抗震设计中应进行重点关注。由图13可以看出:桥梁杆系模型和多尺度模型桥梁拱肋最大地震动时程响应曲线吻合良好,说明了多尺度模型能很好地反映桥梁拱肋地震响应特征。
3.4 拱梁结合段地震响应
拱梁结合段起到连接双拱段拱肋、主梁和基础的重要作用,结构受力复杂,因此,对其进行精细化建模分析。在板壳单元建模过程中,不可避免的存在着由圆弧以及直角构造带来的某些微小单元的应力奇异现象,但这些点对结构整体的应力响应不会带来影响,在分析时对这些极微小单元做忽略处理。
由于该节段所处的特殊位置,地震作用下,其变形主要为拱梁结合段内大横梁中部竖向位移,竖向位移云图及最大时程响应如图14所示;拱梁结合段最大竖向位移响应值为-11.1 cm;其余两个方向位移都较小,仅为1~2 cm,此处不进行讨论。

图14 拱梁结合段竖向位移云图及最大位移时程Fig. 14 Vertical displacement cloud map and maximum displacement time history of arch-beam joint section
地震作用下拱梁结合段最大应力出现在拱梁结合段内大横梁与拱肋部分连接部位,地震作用下拱梁结合段应力云图及最大应力响应时程曲线如图15所示,其最大应力响应值为395.7 MPa。
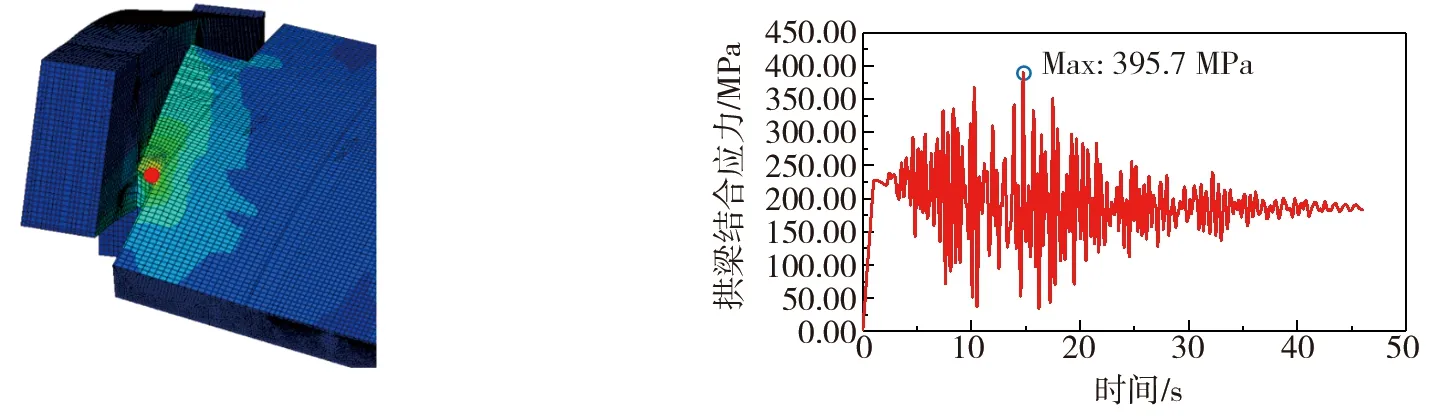
图15 拱梁结合段应力云图及最大应力时程Fig. 15 Stress cloud diagram and maximum stress time history of arch-beam joint
3.5 拱肋分叉段地震响应
拱肋分叉段起到连接拱肋单拱段与双拱段的作用,结构形式与受力较为复杂,因此,对此处进行精细化建模分析。在板壳单元建模过程中,不可避免的存在着由圆弧以及直角构造带来的某些微小单元的应力奇异现象,但这些点对结构整体的应力响应不会带来影响,在分析时对这些极微小单元做忽略处理。
地震作用下,拱肋分叉段位移及应力云图如图16所示。由图16可知:拱肋分叉处最大纵向位移位于拱肋分叉段底部;最大横向位移位于拱肋分叉段双拱侧起始位置内侧;最大竖向位移位于拱肋分叉段最右侧位置内侧;拱肋分叉段起到连接拱肋单拱段与双拱段的重要作用,同时也因其独特的空间构造,地震作用下,在其分叉交点位处应力响应远大于其余位置。地震作用下,拱肋分叉处最大纵向、横向、竖向位移与应力时程曲线如图17所示。由图17可知:拱肋分叉处最大顺桥向位移响应值为-14.1 cm;最大横桥向位移响应值为31.8 cm;最大竖向位移响应值为-25.2 cm;拱肋分叉段最大应力响应值为274.9 MPa。
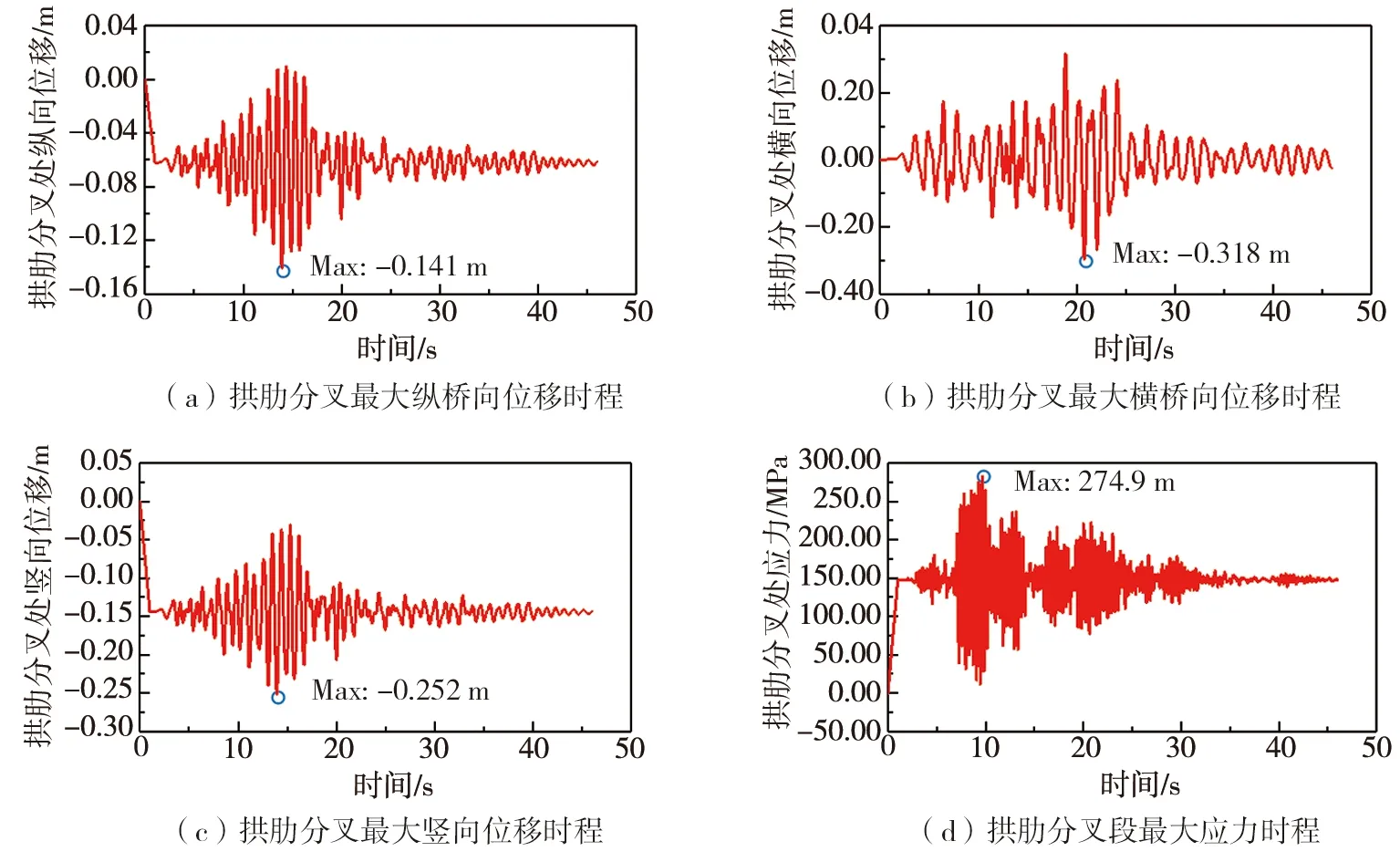
图17 地震作用下拱肋分叉段最大位移与应力时程Fig. 17 Maximum displacement and stress time history of arch rib bifurcation section under earthquake
4 结语
本文针对某空间Y型拱桥,基于桥梁多尺度模型和杆系模型建模方法,采用有限元仿真软件ABAQUS,分别建立杆系模型和多尺度有限元模型。通过两种模型桥梁动力特性对比分析,验证了桥梁多尺度连接方法的正确性。采用时程分析法,计算分析了单向地震动及双向地震动作用下空间Y型拱桥整体和局部关键部件的内力、位移响应,得出了空间Y型拱桥桥梁地震响应规律及抗震薄弱部位,主要结论如下:
1)本文针对空间Y型拱桥建立的多尺度模型能够较好的反映结构的动力特性及地震响应特点,相比于杆系模型,能够更进一步的体现复杂部位的应力状态和损伤程度,具有更高的计算精度。
2)空间Y型拱桥整体地震响应以主梁竖向弯曲和钢拱肋竖向、横向弯曲为主,与桥梁低阶振型的变形特点较为一致。
3)空间Y型拱桥拱肋横向抗弯刚度较弱,钢拱肋分叉部位交叉点与主梁和拱肋结合段处在地震作用下出现应力集中现象,在设计应予以考虑。
