基于拟动力法考虑土体张拉截断的边坡抗震稳定性上限分析
2023-08-18梁承龙
梁承龙,刘 芳
(广西交通职业技术学院 土木建筑工程学院,南宁 530012)
0 引言
近年来,边坡失稳造成的滑坡事件屡见不鲜,其破坏性强以及发生频率高,直接威胁着周边人民的人身安全和正常生活,滑坡事件已成为灾害治理的重点[1-3]。目前,极限平衡法、有限元法以及极限分析法是国内外学者们解决边坡失稳问题最常见的数值和解析方法,而极限分析法相较于其他两种常规方法有着既简易又合理的优点,分析问题时不必考虑土体内部复杂的应力状态,只需构建一个运动学许可的速度场便可求解极限荷载的上限解答,进而确定边坡是否稳定。在众多岩土体本构关系中,Mohr-Coulomb(M-C)屈服准则广受工程师和学者们的青睐,其包含两个抗剪强度指标:粘聚力c和内摩擦角φ。基于M-C屈服准则,CHEN[4]证明了在二维情况下边坡最危险滑动面是一条对数螺旋线。学者们采用该对数螺旋破坏机制进行了大量边坡稳定性分析[5-7]。戴自航等[8-9]通过分析边坡土体内部的应力状态得出在边坡失稳时往往坡顶后缘下一定深度范围内土体受到拉应力作用,导致岩土体受拉破坏,因此将整个滑动面上都视为剪切破坏所得结果偏于保守且与实际土体破坏状态不相符,边坡失稳时实际上是张拉-剪切复合破坏,并运用有限元法结合案例证明了考虑土体张拉破坏的必要性。因此,基于张拉-剪切破坏模型的边坡稳定性分析不断涌现[10-13]。例如,王伟等[14-15]采用应变软化模型考虑边坡失稳时张拉-剪切渐进破坏过程并计算边坡安全系数以及搜索临界滑动面。除此之外,DUNCAN等[16]提出两种方法考虑边坡后缘的受拉破坏:其一,在边坡坡顶处引入一条垂直张拉裂缝;其二,对受拉区的岩土体抗拉强度进行折减,即张拉截断。方法一表明滑动面由对数螺旋线和垂直张拉裂缝组成以消除边坡后缘的受拉区。UTILI[17]综合分析了裂缝的深度和位置对边坡稳定性的影响;MICHALOWSKI[18]考虑了边坡失稳时裂缝的形成过程对边坡稳定性的影响;HE等[19]将二维情况下裂缝边坡稳定性分析拓展到三维情况;饶平平等[20]对裂缝边坡的三维破坏模式进行了拓展;基于拟静力法,HE等[21]和LI等[22]对裂缝边坡的三维抗震稳定性进行研究,绘制出了稳定性图表;基于拟动力法,HOU等[23]基于离散运动学机构研究非均质裂缝边坡的稳定性,分析了拟动力法参数对安全系数的影响规律,探讨了拟动力法与拟静力法的差异,表明拟动力法更符合实际,因其能考虑地震随时空变化的动力特性和地震波在岩土层内传播时土层振动相位差和振幅加速度放大效应。方法二是张拉截断,即将土体的抗拉强度从M-C屈服准则中削弱或去除。DRUCKER等[24]首次将张拉截断引入边坡稳定性分析中;MICHALOWSKI[25]分析了土体张拉截断对边坡稳定性的影响规律并得出孔隙水压力作用下完全张拉截断会导致陡坡的稳定系数将下降至少50%;PARK等[26]分析了考虑张拉截断的岩质边坡三维稳定性问题;ZHANG等[27]对张拉裂缝和张拉截断所得结果进行对比分析。基于拟静力法,学者们对地震作用下考虑张拉截断的边坡临界地震加速度进行求解[28-31],在此基础上结合工程实例,采用Newmark法计算地震效应下边坡的永久位移,得出考虑张拉截断的M-C屈服准则计算所得边坡永久位移是采用线性M-C屈服准则的计算结果2倍之多。然而,考虑张拉截断的边坡稳定性分析大多基于拟静力法,未能考虑地震随时间和空间变化的动力特征。
鉴于此,本文考虑完全张拉截断以去除土体的抗拉强度,并基于拟动力法对边坡进行抗震稳定性分析。在极限分析理论框架下,采用“点到点”的方法构建离散运动学破坏机构[32-33],并建立能量平衡方程,结合强度折减法对地震作用下边坡的安全系数进行求解。通过二分法和优化算法计算所得结果与拟静力法进行对比分析,并对比张拉截断和张拉裂缝两种方式下的边坡安全系数和临界滑动面,探讨拟动力法参数和张拉截断效应对边坡稳定性的影响规律,以期为实际工程提供一定的参考。
1 土体屈服准则
边坡稳定性分析中认为边坡失稳时滑动面上任意一点土体所受到的剪应力超过其抗剪强度而发生剪切破坏。实际边坡失稳破坏时往往在坡顶后缘一定深度范围内会发生张拉破坏[8],而M-C屈服准则仍将这一部分张拉破坏视为剪切破坏,所得到的滑动面为剪切滑动面,未能真实地反映边坡的失稳状态。同时,土体的抗拉强度并不是由试验直接测量得出的,而是根据M-C屈服准则由土体压缩状态向拉伸状态外推得出的结果,远大于土体的实际抗拉强度,不能真实地反映出土体的抗拉强度,因此在边坡稳定性分析中需要对所得的抗拉强度进行折减[25]。如图1所示,根据M-C屈服准则,可以得到土体三轴抗拉强度f3t=c/tanφ和单轴抗拉强度ft=2ccosφ/(1+sinφ),并引入张拉截断折减系数ξ对土体抗拉强度进行折减[25],此时,M-C屈服准则由直线和一段圆弧组成,剪胀角δ则从φ变化到90°,折减后土体抗拉强度可表示为:
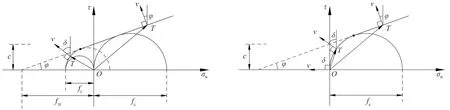
图1 土体张拉截断包络线Fig. 1 Cut off envelope of soil mass by tension
(1)
式中: 0≤ξ≤1,当ξ=1时表示线性M-C屈服准则,当ξ=0时表示完全张拉截断,即土体的抗拉强度为0,也是本文研究的重点。
以下对剪胀角δ进行说明。极限分析定理要求土体屈服时满足相关联流动法则,即各个点的塑性应变增量方向为该点塑性势面的外法线方向,而张拉截断概念的引入会造成屈服面可能有拐角或尖角,导致法线方向不是唯一确定的,但对极限分析并不造成障碍[7]。由于假设土体满足M-C屈服准则,土体发生剪切破坏时必定伴随着体积膨胀,根据几何关系可得塑性应变增量方向与滑动面成角度φ,即认为土体剪胀角δ=φ,此时δ大于土体实际剪胀角,从而高估土体的体积应变,但所得结果仍是一个严格的上限解答。而引入张拉截断的概念会导致δ由φ变化到90°,这是由于土体发生破坏时需满足相关联流动法则所造成的结果,意味着运用极限分析允许发生较大的体积应变,土体发生断裂破坏,区别于塑性屈服,计算所得结果仍是真实极限荷载的上限解答[34-35]。PUAL[36]认为考虑张拉截断的M-C屈服准则是描述土体发生断裂的状态而不是土体发生屈服的状态。因此,在张拉截断部分将δ理解为破裂角以区分剪胀角的概念。
2 边坡安全系数的上限解答
极限分析上限定理可描述为对于任意一个满足运动学许可的速度场,从能量平衡角度建立平衡方程,可以获得极限荷载的上限解答。因此,根据所建立的运动学许可的破坏机构,计算边坡发生失稳瞬间的外力做功功率和内能耗损率,通过建立能量平衡方程可以得到边坡安全系数的上限解答。在本文中,边坡土重和地震力做功为外力做功功率;内能耗散率只考虑边坡潜在滑动面瞬时滑动所产生的能量。
2.1 离散机构的构建
在二维情况下,传统上限法假设滑动面为对数螺旋线滑动面,进而再求解边坡稳定系数或安全系数。不同于传统上限法,本文不再假设滑动面形状,通过“点到点”方法递推出一系列离散点相连逐步构成滑动面[32-33],因此滑动面不再是光滑连续曲线,而是许多微小的直线段的组合,其优势在于这种构成滑动面的方法能很好地处理土体内摩擦角非均质性对滑动面的影响。如图2所示,以边坡坡趾A为坐标原点建立直角坐标系,边坡高度为H,坡角为β。本文假设滑动面经过A,即边坡发生坡趾破坏,在此基础上,建立边坡离散运动学破坏机构,并具体给出“点到点”生成滑动面的推导过程。
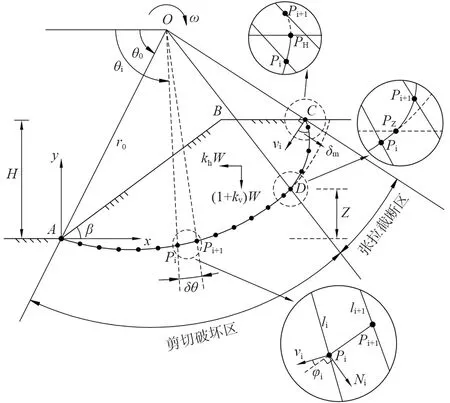
图2 离散运动学许可破坏机构[25]Fig. 2 Discrete kinematics Permit Destruction Mechanism
边坡失稳时滑动土体视为刚体且满足考虑土体完全张拉截断的M-C屈服准则,并以角速度ω绕点O作旋转破坏。根据所建立的直角坐标系,旋转中心点O的坐标可由变量r0和θ0确定:
(2)
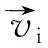
(3)
由于本文考虑土体抗拉强度完全折减,因此引入变量Z来描述完全张拉截断部分滑动面的深度,深度为H-Z,如图2所示。完全张拉截断部分的破裂角δ采用与离散点的纵坐标呈线性关系表示[25],因此,整个滑动面的破裂角δi分布可表示为:
(4)
式中:δm为坡顶C处的破裂角,φZ为高度为Z处的土体内摩擦角。当yi≤Z,表示土体发生剪切破坏,当yi>Z时,采取线性插值方法调整yi=Z,如图1中点D所示;以D作为起始点,土体发生断裂,当yi>H时,同样采取线性插值方法调整yi=H,结束滑动面的生成。
2.2 外功率
外功率包括滑动土体自重做功功率和地震力做功功率。计算简图如图3所示,其中:c0和φ0分别为坡顶处粘聚力和内摩擦角,ch和φh分别为坡趾处粘聚力和内摩擦角。相较于传统对数螺旋破坏机构,本文所构建出的“点到点”离散破坏机构的优势在于分析内摩擦角非均质性的边坡稳定性,例如成层边坡或者内摩擦角随深度变化的边坡。因此,本文针对均质边坡和非均质边坡进行稳定性分析与对比。其中:均质边坡定义为边坡横截面上粘聚力和内摩擦角保持不变,即c0=ch,φ0=φh;非均质边坡定义为边坡横截面上粘聚力和内摩擦角随深度线性增加。

图3 计算简图Fig. 3 Calculation diagram
2.2.1 土体自重做功功率
对滑动土体ABC分割成若干个梯形块体,即对于滑动面AC上相邻两个离散点Pi和Pi+1作平行线交边坡坡面于点Qi和Qi+1从而形成梯形块体PiPi+1Qi+1Qi。因此,滑动土体自重功率Wγ可用离散梯形块体的自重功率之和:
Wγ=ω∑γiAi(xGi-xO)
(5)
式中:γi为第i个梯形块体重心处的土体重度,Ai为第i个梯形块体面积,xGi为第i个梯形块体重心的横坐标。
2.2.2 地震力做功功率
由于拟静力法忽略了地震力随时间变化及地震波在土体中传播的特性,本文采用拟动力法来描述地震力的动力特征[23]。拟动力法假定土体的剪切模量为常数,水平和竖直地震加速度分别与地震剪切和纵波波速有关,水平和竖直地震加速度简化为正弦函数,其大小会随着时间呈周期变化,可以较好地体现地震波随时间循环变化的规律,同时,拟动力法还考虑了土体对地震波的放大效应,因此拟动力法能更好地描述边坡的动态稳定性[37-40]。因此,t时刻第i个梯形块体的水平地震加速度系数kh和竖向地震加速度系数kv分别表示为:
(6)
(7)
式中:ah和av分别为水平和竖向地震加速度,VS和VP分别为地震剪切和纵波波速,f为土体放大系数,T为地震波周期。文献[41]表明:计算过程中竖向地震加速度可作为水平地震加速度的一个分量表示,因此,kv=λkh,λ为竖向与水平地震加速度系数比例系数,本文λ设置为0.5。与滑动土体自重功率推导过程相同,水平和竖向地震力做功功率可表示为:
Weh=ω∑γiAi·kh·(yO-yGi)
(8)
Wev=ω∑γiAi·kv·(xGi-xO)
(9)
式中:Weh和Wev分别为水平和竖向地震力功率,yGi为第i个梯形块体重心的纵坐标。
2.3 内能耗散率
由于滑动土体沿滑动面做刚体转动,因此内能耗散率只发生在滑动面AC上,可表示为[25,29]:
(10)
式中:ci为点Pi处的粘聚力,Li为滑动面PiPi+1的长度,Ri为OGi的长度。
2.4 安全系数
根据能量平衡方程,令外功率等于内能耗散率,如式(11)所示,结合强度折减法计算边坡的安全系数,通过土体的实际抗剪强度参数c和tanφ分别除以折减系数FS,可以得到土体处于极限平衡状态下的抗剪强度参数c′和tanφ′,如式(12)所示,并定义FS为边坡安全系数。
Wγ+Weh+Wev=D
(11)
(12)
式(11)是关于FS的非线性隐函数,变量为θ0、r0、δm、Z和t。利用MATLAB编写迭代程序,通过二分法和优化算法可以快速精确地得出边坡安全系数FS的值,确定滑动面的位置,具体优化过程详见文献[32]。
3 对比验证
为了证明本文公式推导和计算结果的正确性和有效性,与文献[25,33]中所得结果进行对比验证。首先,对不考虑土体张拉截断情况下的边坡稳定性进行对比。图4所示为基于拟动力法不同f,T和λ对临界水平地震加速度khc的影响对比,khc的表达式可结合式(5)-式(11)得到:

图4 边坡临界水平地震加速度对比
(13)
边坡相关参数为:β=40°,H=10 m,γ0=14 kN/m3,γh=22 kN/m3,c0=15 kPa,ch=30 kPa,φ0=10°,φh=20°,λ=0.5,T=0.3 s,t0=0,f=1.5,VS=150 m/s,VP=280.5 m/s。其中:f的范围为1.0~1.8,T的范围为0.2~0.4 s,λ的范围为-1.0~1.0,并按式(14)进行归一化处理为无量纲形式:
(14)
式中:x′为归一化结果,x为输入参数,xmin为参数最小值;xmax为参数最大值。图4表明本文计算所得khc与文献[33]结果吻合度很高,且khc随着f、T和λ的增大而减小,进一步说明地震周期T和土体放大系数f在边坡抗震稳定性分析中的重要性。表1所示为在静力状态时考虑土体张拉截断情况下的边坡临界高度Hcr的对比,文献[24]通过构建传统对数螺旋破坏机构求解边坡稳定系数γH/c,为了便于计算结果比较,令c/γ=1.0,将文献[24]结果转化为边坡临界高度Hcr。边坡相关参数为:γ=20 kN/m3,c0=ch=20 kPa,φ0=φh=20°,kh=0.0。由表1可知: 本文所得的结果与文献[25]结果十分接近且略小于文献[25]结果,最大误差不超过3.1%,主要原因在于破坏机构构建的形式不同导致在土体张拉截断区域对破裂角δ所采用的分布不同。文献[24]认为张拉截断区域的δ随角度呈线性分布(文献[24]和式(8))并表明相较于非线性分布,线性分布所得结果为最优解;而本文认为张拉截断区域的δ与离散点高度呈线性分布。图4和表1的对比结果说明了本文方法的正确性和有效性。

表1 完全张拉截断边坡稳定系数对比(c/γ=1.0)
4 结果分析
4.1 拟动力法与拟静力法对比
由于拟静力法概念清晰和计算简便,被广泛应用到实际边坡工程的抗震稳定性分析中。但其忽略地震随时间变化的动力特性以及土体剪切模量和剪切波波速视为无穷大会造成高估建(构)筑构的抗震稳定性。因此,首先对比均质边坡与非均质边坡在拟动力法和拟静力法下的安全系数FS。对于均质边坡,相关参数为:H=5 m,γ=20 kN/m3,c0=ch=15 kPa,φ0=φh=20°,λ=0.5,T=0.3 s,t0=0,f=1.4,VS=150 m/s,VP=280.5 m/s。对于非均质边坡,相关参数为:H=5 m,γ=20 kN/m3,c0=10 kPa,ch=15 kPa,φ0=15°,φh=20°,λ=0.5,T=0.3 s,t0=0,f=1.4,VS=150 m/s,VP=280.5 m/s。图5所示为具有不同坡角β边坡安全系数FS的拟动力法和拟静力法结果对比。从图5可以看出: FS随着水平地震系数kh和β的增大而减小,说明边坡越陡且地震强度越大会大幅度降低边坡的稳定性。同时,拟静力法结果高于拟动力法结果,且随着kh的增大,两者结果的差异增大。这是由于拟静力法将随地震力简化为恒定惯性力作用在边坡上,忽略了地震波周期T,土体放大系数f等对地震加速度的影响,导致地震力做功减小,FS增大。例如对于β=60°均质边坡,kh=0.1和kh=0.3对应的拟静力法结果分别高出其拟动力法结果2.95%和7.73%,说明在强震作用下采用拟静力法会大大高估边坡的抗震稳定性。除此之外,图5给出了折减系数ξ=0.0和ξ=1.0情况下边坡FS的拟动力法结果对比,表明考虑土体完全张拉截断会降低FS。由于线性M-C屈服准则将土体张拉破坏视为剪切屈服,导致高估了土体的抗拉强度;而考虑土体完全张拉截断的M-C屈服准则使得土体张拉破坏部分能以断裂的形式表现出来,用以区别剪切破坏,能体现出边坡失稳瞬间的状态。

图5 不同坡角对边坡安全系数的影响Fig. 5 Impact of different slope angles on slope safety factor
4.2 拟动力法参数分析
为进一步探讨拟动力法对边坡稳定性的影响,以坡角β=60°非均质边坡为例,分别改变明地震周期T和土体放大系数f以分析FS的变化。图6所示为不同地震波时间T对FS的变化影响。由图可知:kh取值不同时,FS随T的增大而减小,原因在于T增大,地震波在一个周期内持续时间增加,导致地震力做功增加,从而FS下降。除此之外,FS在T=0.1~0.2 s内变化幅度较大,并随着kh的增大幅度变化显著。同时,由于简化为正弦函数的水平和竖直地震加速度在T≥0.3 s时正弦函数部分约等于1,因此水平和竖直地震加速度变化幅度很小,导致地震力做功功率基本保持不变,因此FS在T=0.3 s后基本保持不变。如图7所示,FS随土体放大系数f的增大呈下降趋势,原因在于f越大,地震波在土体里传播的加速度幅值越大,导致地震力做功功率增大,对边坡造成不利影响加大,并且kh的增大会增加FS下降的幅度,例如。当ξ=0.0,kh=0.1时,f由1.0增大到1.8,FS下降了6.37%;当kh=0.3时,FS下降了18.36%。由此可知: 强震作用下较大的f会大幅度削弱边坡的稳定性,造成严重滑坡灾害。除此之外,图6-7再次表明了土体完全张拉截断效应会削弱边坡稳定性,且削弱幅度随着f和kh的增大而增大。在均质边坡中体现出类似的规律,故不再赘述。
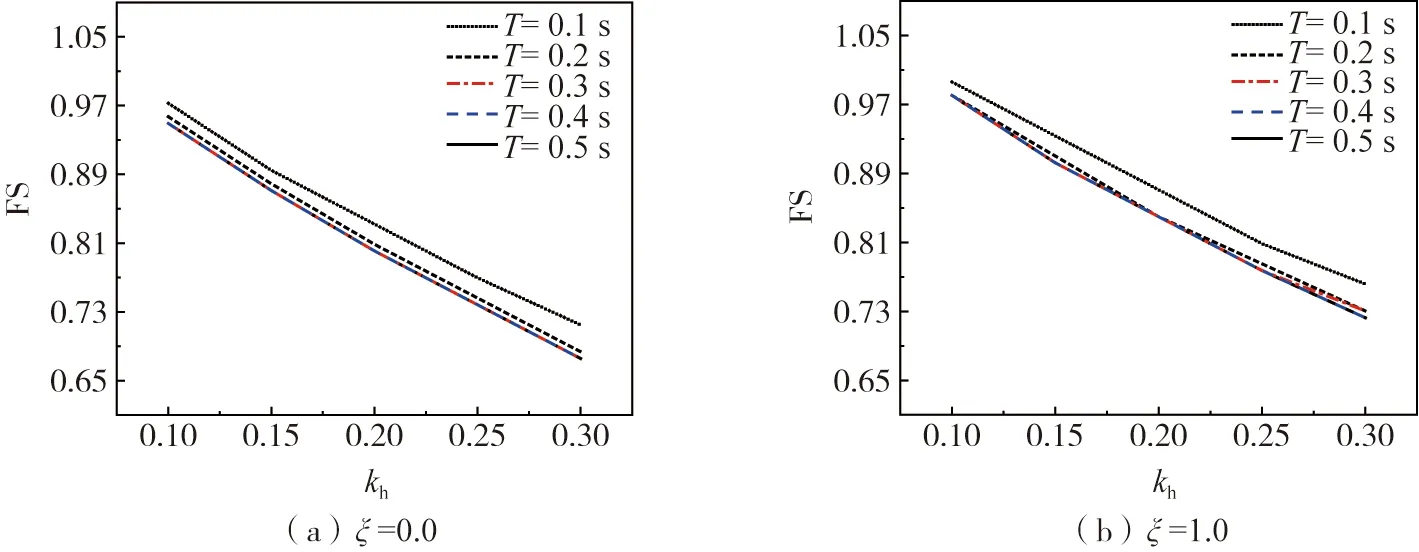
图6 不同地震波周期对非均质边坡安全系数的影响Fig. 6 Impact of different seismic wave periods on the safety factor of heterogeneous slopes

图7 不同土体放大系数对非均质边坡安全系数的影响Fig. 7 Effect of different soil magnification factors on the safety factor of heterogeneous slope
4.3 不同折减方式对比
图8所示为消除土体抗拉强度的两种方法的FS对比:其一为本文方法,即完全张拉截断;其二为在坡顶处引入一条垂直张拉裂缝。由图8可知:两种方法所得FS非常接近,相差不超过4%,在工程允许范围之内。由于边坡引入张拉裂缝建模更为简便,因此在工程实践中可采取此方法快速获取裂缝边坡的安全系数。同时,边坡稳定性分析另一个核心内容为求解边坡失稳瞬间的临界滑动面。图9给出了kh=0.0和kh=0.2情况下两种方法所得的临界滑动面。图9表明虽然两种方法所得FS基本相同,但其临界滑动面差异很大。当kh=0.0时,均质边坡和非均质边坡的临界滑动面基本一致;而两种方法所得的临界滑动面差异明显。完全张拉截断区域深度小于张拉裂缝的深度约20%,造成的滑动土体体积高出张拉裂缝滑动土体体积约14%。当kh=0.2时,均质边坡临界滑动面比非均质边坡临界滑动面更浅,说明强震作用会放大土体的非均质性对临界滑动面的影响。但完全张拉截断区域深度大于张拉裂缝的深度约60%,造成滑动土体体积高出张拉裂缝滑动土体体积约10%。由此可知:引入张拉裂缝的临界滑动面比完全张拉截断的临界滑动面更浅,边坡失稳时滑动土体体积较少,边坡的破坏规模较小。因此,引入张拉裂缝方法会低估边坡的破坏规模,低估了对边坡失稳后所造成的灾害,导致防灾措施不充分,造成大量人员伤亡和财产损失。因此,对边坡破坏规模的评估应采用完全张拉截断方法。
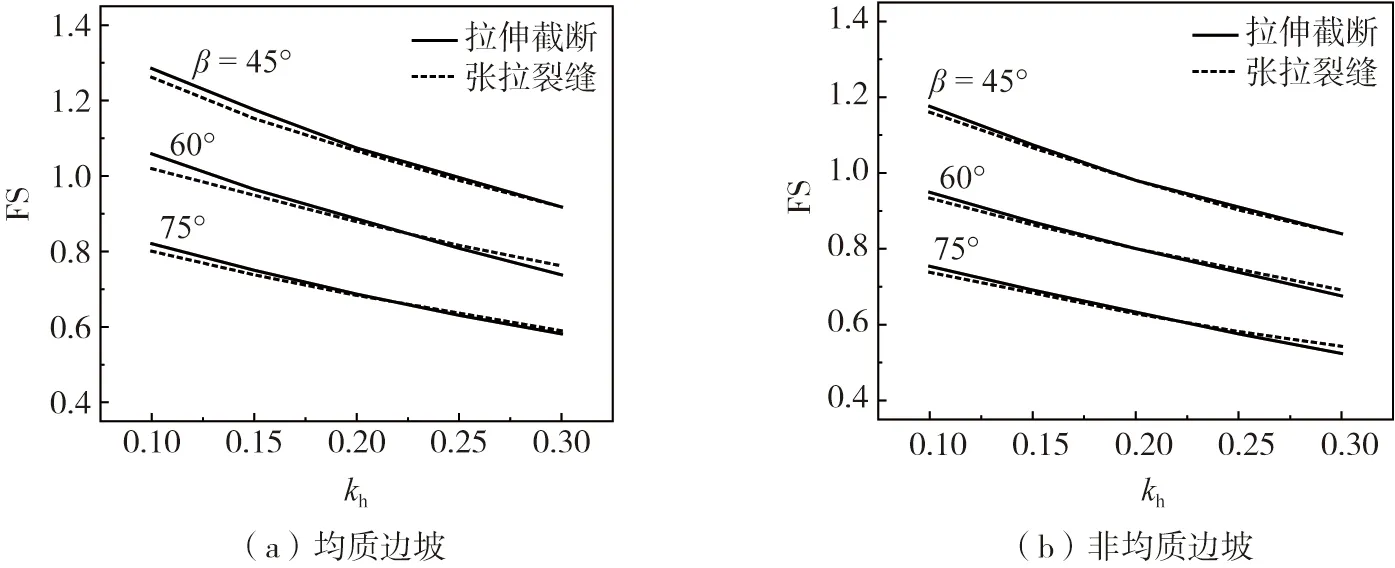
图8 不同折减方式对边坡安全系数的影响Fig. 8 Impact of different reduction methods on slope safety factor
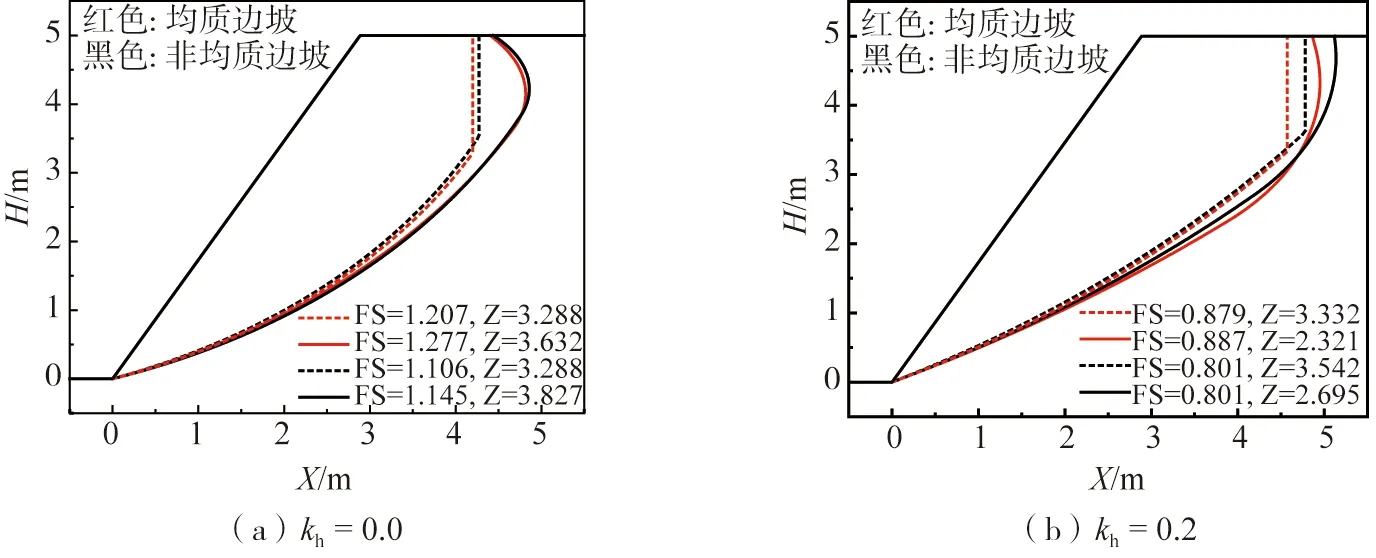
图9 不同折减方式对边坡临界滑动面的影响Fig. 9 Effect of different reduction methods on the critical sliding surface of slope
5 结论
本文通过引入完全张拉截断以去除Mohr-Coulomb屈服准则中高估的土体抗拉强度。基于极限分析上限定理,以“点到点”的方式构建离散运动学破坏机构解决土体内摩擦角非均质性对边坡稳定性影响的问题,运用拟动力法对边坡的抗震稳定性进行研究。采用二分法和优化算法并结合强度折减法求解边坡安全系数及临界滑动面。得出主要结论如下:
1) 由于忽略地震的动力特性和土体放大系数,拟静力法所得结果高于拟动力法所得结果,且在强震作用会加大两者计算结果的差异,说明强震作用下采用拟静力法会明显高估边坡稳定性。同时,边坡安全系数随土体放大系数f的增大而增大,并在T≥0.3 s基本保持不变。
2) 相较于线性M-C屈服准则,考虑土体完全张拉截断可以将滑动面张拉破坏区域以断裂的形式表示,区别塑性剪切屈服区域,并且土体完全张拉截断会降低边坡安全系数。
3) 考虑土体完全张拉截断与引入垂直张拉裂缝两者所得边坡安全系数基本一致,但临界滑动面区别明显。在静力状态下完全张拉截断区域深度小于张拉裂缝深度;反之,在动力状态下大于张拉裂缝深度。考虑土体完全张拉截断的临界滑动面更深,滑动土体体积更多,表明边坡失稳时破坏规模更大。引入垂直张拉裂缝建模简单,可快速获得裂缝边坡安全系数;考虑土体完全张拉截断可用来评估滑坡规模。
