脉冲地震下简支梁桥倒塌过程及响应分析
2023-08-18游四方岳伟勤胡洋郑史雄鲁玉忠
游四方,岳伟勤,胡洋,郑史雄,鲁玉忠,杨 磊
(1. 黄河勘测规划设计研究院有限公司,河南 郑州 450003; 2. 中铁长江交通设计集团有限公司,重庆 401121;3. 蜀道投资集团有限责任公司,四川 成都 610041; 4. 西南交通大学 土木工程学院,四川 成都 610031)
0 引言
我国的地震断裂带众多且十分活跃,考虑到修建成本、工程进度和地形地貌等条件的影响和约束,某些结构会不可避免出现靠近断层的情况,受到断层地震动的影响显著[1]。并且随着西部开发战略和城镇化建设的推进,交通系统不断完善,铁路和公路网络纵横交织,这使得作为现代交通“咽喉”的桥梁结构得到了广泛发展[2]。简支梁桥结构简单,其凭借施工质量好和效率高的优势,作为城市高架桥和引桥的基本体系,广泛应用于公路铁路系统[3]。
桥梁倒塌会导致道路交通进入瘫痪,严重影响抗震救灾进程。因此,国内外研究学者对桥梁倒塌进行了相关研究。黎雅乐[4]基于振动台实验和有限元模拟,对强震作用下连续梁桥的动力特性、灾变机理、倒塌准则和倒塌控制方法等进行了系统性研究,揭示了简支梁桥的倒塌破坏模式;范振华[5]为评估地震作用下高墩刚构桥的抗倒塌能力,提出了基于墩顶竖向位移的倒塌破坏判断准则;林远铮等[6-7]通过振动台实验和LS-DYNA数值模拟,系统研究了断层破裂情况下钢-混组合刚构桥的抗震性能;左烨等[8]通过多尺度建模,分析了连续梁桥、简支-连续梁桥及简支梁桥在地震作用下倒塌过程,揭示了三种桥型倒塌过程的机制及区别;罗文文等[9]基于IDA的结构倒塌易损性方法,定量分析了变形准则、刚度准则、Park-Ang损伤指标准则及刚度与变形准则这4种倒塌标准下钢筋混凝土框架结构抗倒塌能力;孙利民等[10]基于显式积分法的非线性有限元软件LS-DYNA,对贵州省高速公路上跨越山谷的曲线T型刚构高墩混凝土桥实现了全桥倒塌过程的仿真;徐俊祥等[11]利用LS-DYNA程序建立数值分析模型,再现土耳其Arifiye大桥在1999年地震中由于地裂引起倒塌的过程,并与真实的倒塌场景进行比较,验证了分析模型的正确性;宗周红等[12]在LS-DYNA软件中建立了大跨度斜拉桥显式有限元模型,对强震作用下大跨斜拉桥增设阻尼器和辅助墩前后的倒塌破坏模式进行了研究。尽管已有不少学者对简支梁桥的倒塌机理进行了研究,但对脉冲地震作用下桥梁倒塌问题的研究较少,成果相对有限[13-14]。因此,模拟脉冲地震下简支梁桥的倒塌过程,研究脉冲参数对简支梁桥的影响对实际工程应用具有重要意义。
综上所述,本文以某简支梁桥为研究对象,基于LS-DYNA平台建立简支梁桥的三维有限元模型,根据脉冲地震特征人工合成不同脉冲幅值和脉冲周期的地震动,模拟脉冲地震作用下简支梁桥倒塌全过程,研究脉冲幅值和脉冲周期对简支梁桥倒塌过程和地震响应的影响。
1 脉冲地震动合成方法
目前,人工合成脉冲地震动的普遍思路是分别模拟地震记录中的低频脉冲成分和高频无脉冲成分,并将二者叠加。许多学者提出了速度脉冲的简化模型,MAKRIS等[15]认为脉冲型地震波是不同周期长度的正弦或余弦波的组合;MENUN等[16]采用分段函数进行非线性回归分析,介绍了一种等效速度脉冲方法;BURKS等[17]从断层地震动中提出滑冲脉冲的预测模型,并将该模型与现有经验模型对比,结果表明该模型与脉冲周期、脉冲幅值模型吻合较好;YANG等[18]提出了一种断层地震动合成方法,并提出了荷载函数的参数选择方法,该方法可以根据桥梁沿断层的位置合理准确地估计了地震需求;MAVROEIDIS等[19]提出的等效速度脉冲模型能精准地模拟破裂前方效应和滑冲效应所引起的单峰值、双峰值和多峰值地面振动,并能适应不同幅值的相邻脉冲;李帅等[20]通过将断层地震动分解得到近断层地震动的高频部分,然后叠加脉冲模型得到人工合成的跨断层地震动;HE等[21]提出了一种用脉冲振幅衰减函数表示的速度脉冲的等效模型。上述速度脉冲模型中,有的模型只考虑了脉冲速度峰值和脉冲周期,有的模型将脉冲的形状调整参数也考虑了在内,而在函数的表达形式上,速度时程通常利用分段函数表示。
由于现有的等效速度脉冲模型通常采用分段函数表示等效速度时程,导致了实际脉冲速度时间过程的曲线拟合流程非常麻烦。此外,一些等效脉冲模型只具有一种形态,不能模拟其他特定的脉冲形状。为了解决这些问题,田玉基等[22-23]提出了单一连续函数来表示脉冲的速度时间过程,并使用5个精确的待定参数表示了速度脉冲的脉冲周期、速度峰值以及形状特征。
为了准确体现脉冲效应,根据随机振动理论将平稳过程乘以包络函数得到非平稳过程。脉冲地震动的合成包括两部分:分别为高频成分和低频脉冲部分。前者可以依据设计反应谱,通过三角级数和包络函数得到高频无脉冲的非平稳地震加速度结果。后者选择田玉基等提出的等效速度脉冲模型,进行低频脉冲地震动的合成,其中等效速度脉冲模型用下式表达:
v(t)=vp·w(t)·cos[2πfp(t-t1)] 0≤t≤T
(1)
式中:vp是速度脉冲的峰值,fp为速度脉冲频率,ω(t)为速度脉冲相位角,T为速度时程的持续时间。速度时程的包络函数由下式确定:
(2)
式中:t0是包络函数的峰值发生时刻,γ表示峰值衰减速度。
通过数值微分对等效速度脉冲结果进行分析得到脉冲加速度时程。调整t0和t1的数值使高频成分和低频脉冲部分加速度最大值出现在同一时刻,然后通过叠加即可得到含有低频脉冲的非平稳地震动时程。图1为脉冲型地震动的合成示意图。
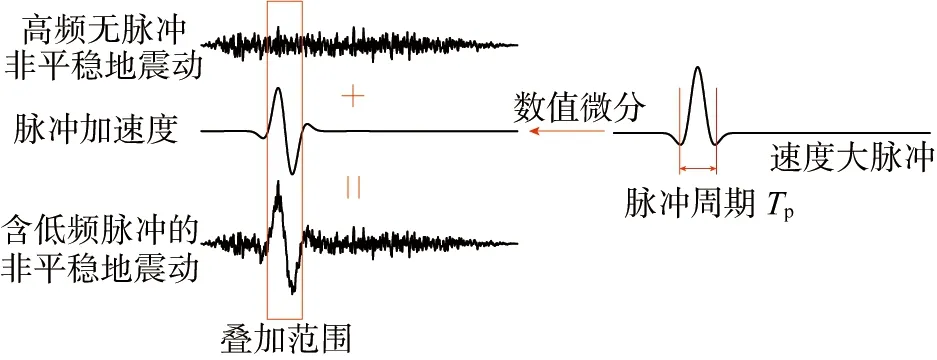
图1 脉冲地震合成Fig. 1 Pulse seismic synthesis
2 工程数值算例
2.1 桥梁简介
以某简支梁桥为实际工程背景,该桥的上部结构为3×30 m的预应力混凝土简支T梁,0号桥台和3号桥台为桩柱式桥台,桥墩为双圆柱墩,墩身高度为22 m。墩台桩基础均按嵌岩桩设计,桩基础嵌入中风化砂岩不小于2.5倍桩径,简支梁桥的全桥布置如图2所示。
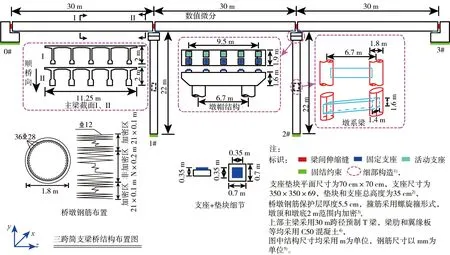
图2 简支梁桥全桥布置Fig. 2 Layout of simply supported beam bridge
2.2 有限元建模
基于ANSYS/LS-DYNA平台建立简支梁桥的三维有限元模型,其中全桥混凝土、支座采用实体单元模拟,钢筋采用梁单元模拟,并对相关结构进行适当简化,不考虑桩土效应。该简支梁桥的有限元模型如图3所示。
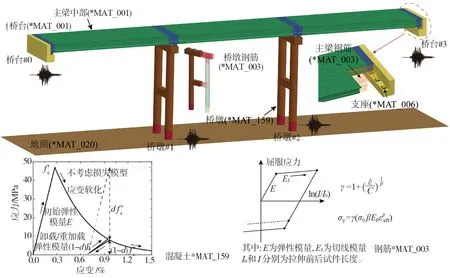
图3 简支梁桥有限元模型Fig. 3 Finite element model of simply supported beam bridge
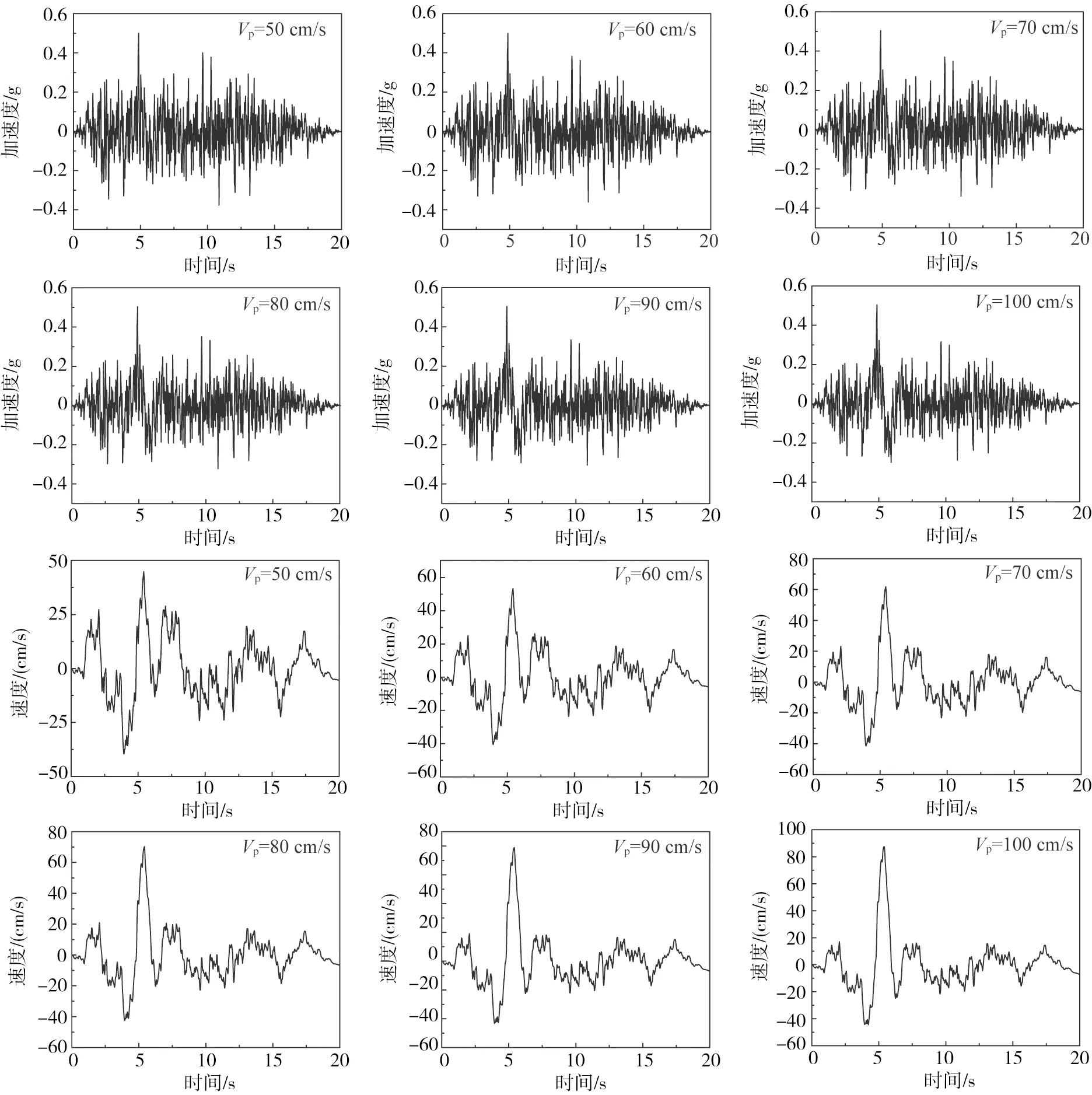
图4 不同脉冲幅值的地震加速度和速度时程曲线Fig. 4 Time history curves of seismic acceleration and velocity with different pulse amplitudes
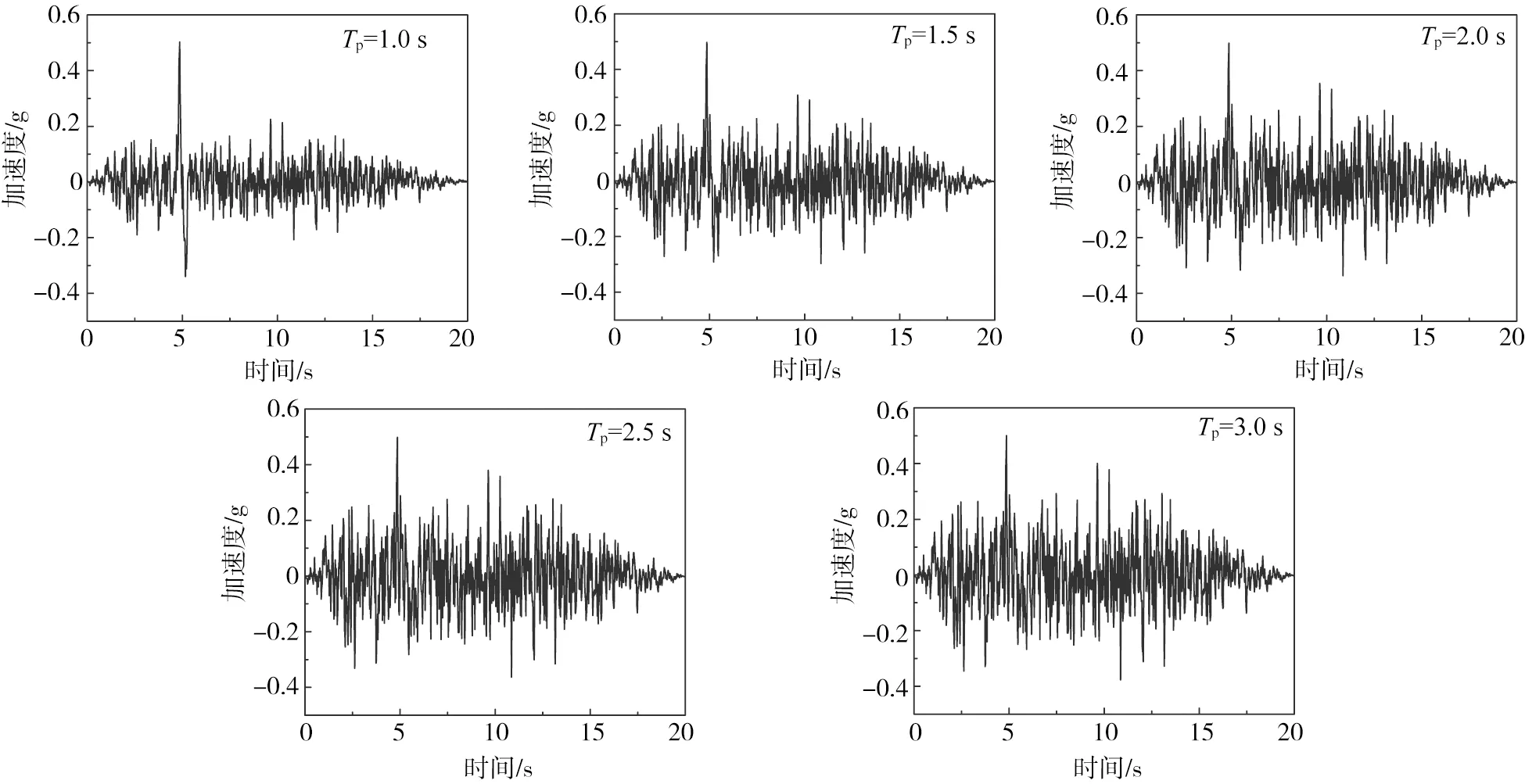
图5 不同脉冲周期的地震加速度和速度时程Fig. 5 Time history of seismic acceleration and velocity in different pulse periods
在ANSYS/LS-DYNA中通常采用关键词*CONTACT_AUTOMATIC_SURFACE_TO_SURFACE进行面面自动接触的模拟,并对摩擦、阻尼、接触时间和罚因子等进行控制。此外,在地震作用下,结构出现破坏后可能出现落梁,并发生主梁与桥墩的碰撞和主梁与地面的接触等,这些都可以通过自动面面接触进行接触定义。除此之外,还应添加关键词*CONTROL_CONTACT对整个模型的接触提供一个全局性的把控,其中包括接触刚度、接触厚度、接触搜寻循环数以及是否考虑初始穿透等问题。针对不同接触问题适当调整参数设置对提高计算精度是很有必要的。
2.3 脉冲型地震动合成
根据人工脉冲地震动合成方法分别合成了不同脉冲幅值和脉冲周期的地震动。为了研究脉冲幅值和脉冲周期对桥梁倒塌过程和地震响应的影响,控制地震动的PGA为0.5 g。合成地震动的参数信息见表1。图4-5分别为不同脉冲幅值和脉冲周期的加速度、速度时程曲线。

表1 人工合成地震参数信息Table 1 Synthetic seismic parameter information
3 结果分析
3.1 自振特性分析
LS-DYNA中进行结构自振特性的计算需采用隐式求解功能。该简支梁桥前6阶模态的频率及振型见表2。从表中可以看出该简支梁桥的振型主要以主梁振动,桥墩弯曲为主。
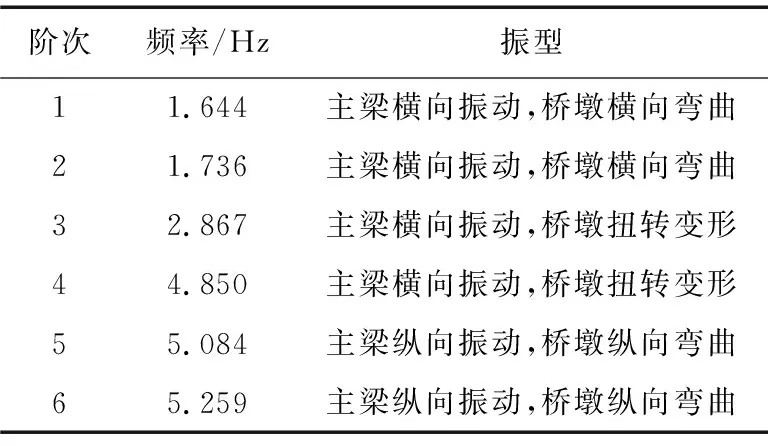
表2 简支梁桥前6阶自振频率及振型Table 2 Frequencies and modes of simply supported beam bridge
3.2 不同脉冲幅值地震下倒塌过程及响应分析
脉冲幅值的大小往往关系到脉冲地震的强弱,幅值越大,脉冲能量越大,越容易导致桥梁破坏。依次取脉冲幅值为 50、60、70、80、90和100 cm/s进行人工脉冲地震动的合成,研究脉冲幅值对简支梁桥的倒塌过程和地震响应的影响。
3.2.1 倒塌过程分析
不同脉冲幅值人工地震作用下简支梁桥倒塌破坏过程大致可以分为三种模式,分别为:墩底出现单元部分失效,但未能演变出倒塌破坏、桥墩墩底单元大规模失效导致桥梁整体倒塌和墩梁相对位移过大而引起落梁破坏。此外,不同的破坏方式与脉冲幅值的大小也存在明显的正相关性。
当Vp=50 cm/s时,简支梁桥支座和墩底部分混凝土虽然有较多单元失效,但在地震加载过程中桥梁整体并没有发生倒塌。
图6为地震峰值加速度所在时刻(t=5.86 s)简支梁桥单元失效情况,可以看到墩底是单元失效较为严重的部位,说明墩底的损伤程度最高。当t=17.34 s时,桥墩没有额外出现大面积单元失效的情况,桥梁结构并没有发生垮塌破坏。
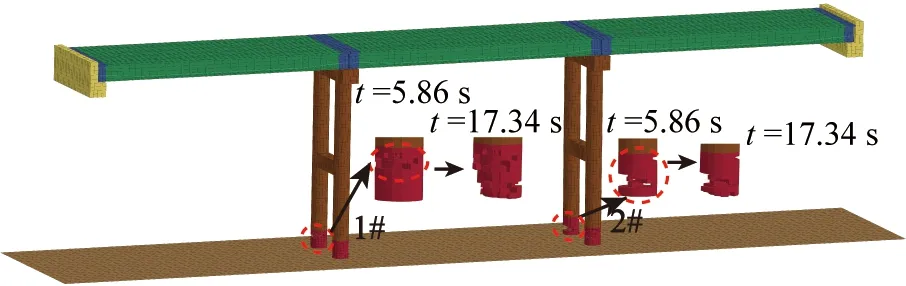
图6 Vp =50 m/s时桥梁倒塌破坏过程Fig. 6 Bridge collapse and failure process when Vp=50 m/s
当Vp=60 cm/s和Vp=70 cm/s时,桥梁的倒塌破坏是由于墩底损伤过大所造成的桥墩倒塌。简支梁桥一侧桥墩因墩底混凝土大面积失效而丧失足够的承载能力,进而导致桥墩倒塌。当Vp=80 cm/s和Vp=90 cm/s时,简支梁桥因某一桥墩两个圆柱墩墩底混凝土大规模失效而发生桥墩倒塌,失去桥墩支撑开始发生落梁破坏。
当Vp=100 cm/s时,破坏模式是桥墩出现损伤后,墩梁相对位移大于主梁的搭接长度而出现的落梁破坏。
图7为Vp=100 m/s时简支梁桥的倒塌过程。当t=17.06 s时,2#桥墩墩底出现了大量混凝土失效,且墩底的转动变形进一步加大了桥墩变形,图(a)中细部图可以看到此时右边跨主梁的搭接长度已经严重不足。当t=17.78 s时,桥墩转动加剧,支撑长度变为零,开始出现落梁。t=19.50 s时,右边跨主梁左端接触到地面的同时撞击到2#桥墩墩底,2#桥墩已经完全丧失了稳定支撑功能,将逐渐演化为简支梁桥的连续倒塌。
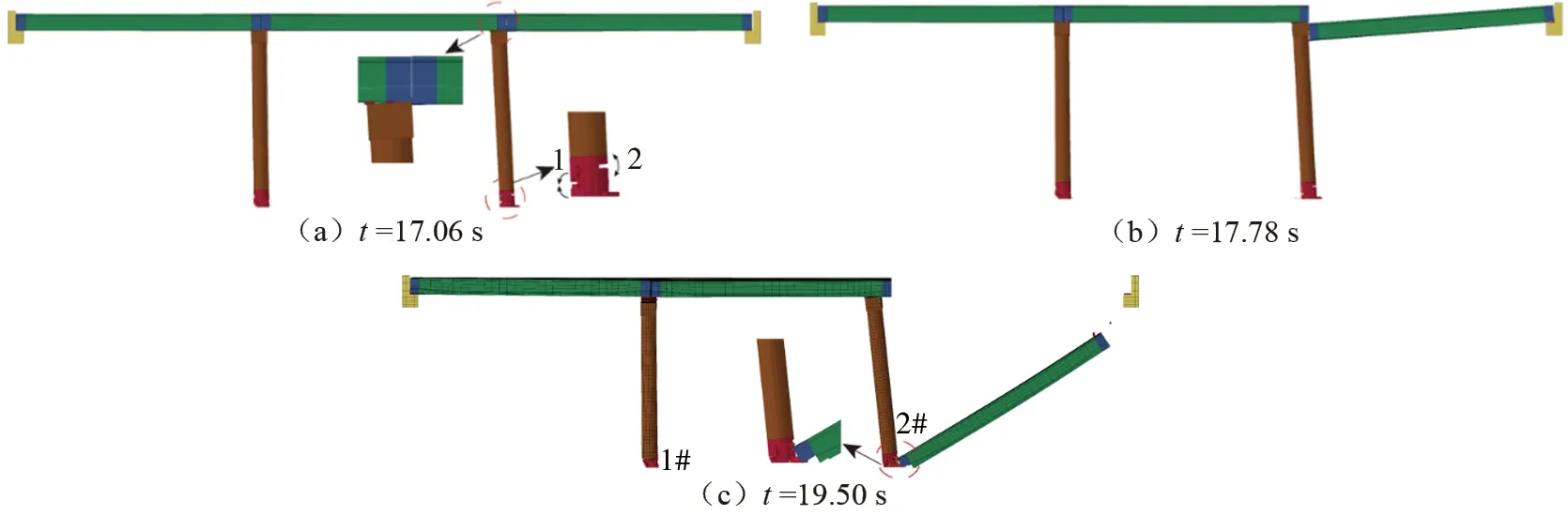
图7 Vp=100 m/s时桥梁倒塌破坏过程Fig. 7 Bridge collapse and failure process when Vp=100 m/s
3.2.2 动力响应分析
考虑到单元失效可能会导致结构变为机动体系,结构内力也会重新分布,故分别提取地震作用下开始出现单元失效前的响应见表3与图8和不考虑单元失效整个地震过程中的最大响应见表4与图9。
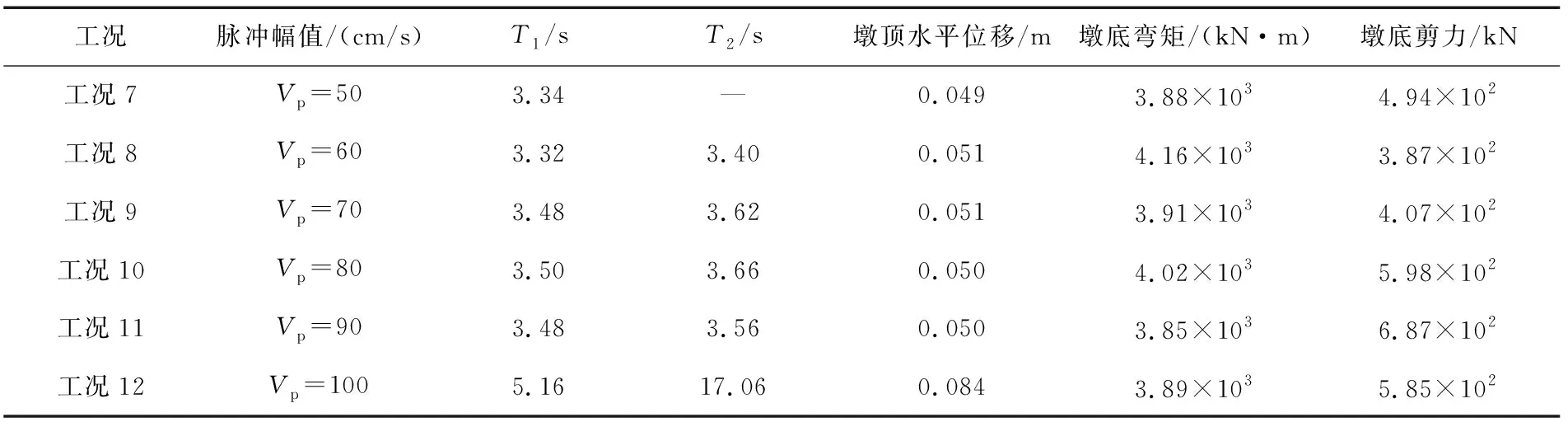
表3 开始出现单元失效前结构地震响应Table 3 Structural seismic response before unit failure
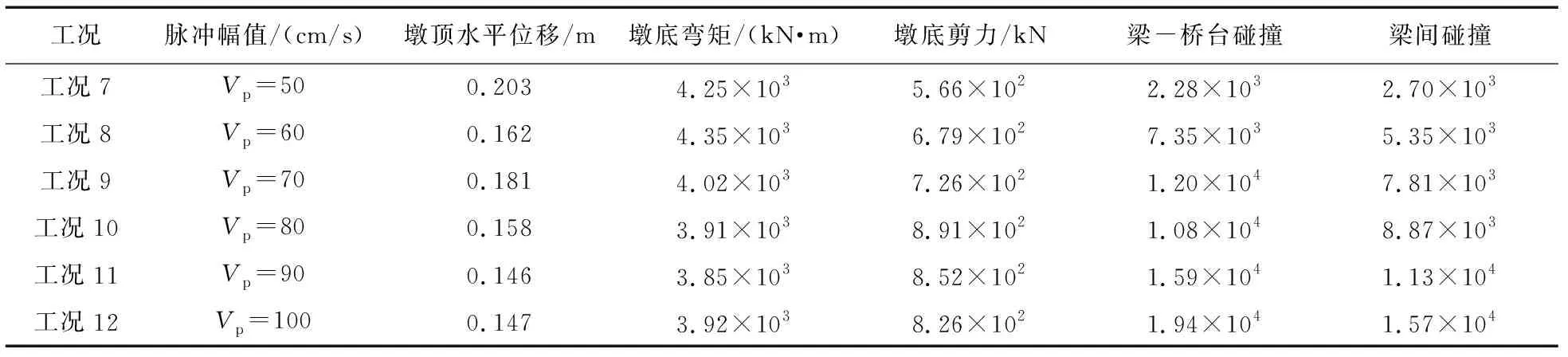
表4 不考虑单元失效时桥梁最大地震响应Table 4 Maximum seismic response of bridge without considering unit failure
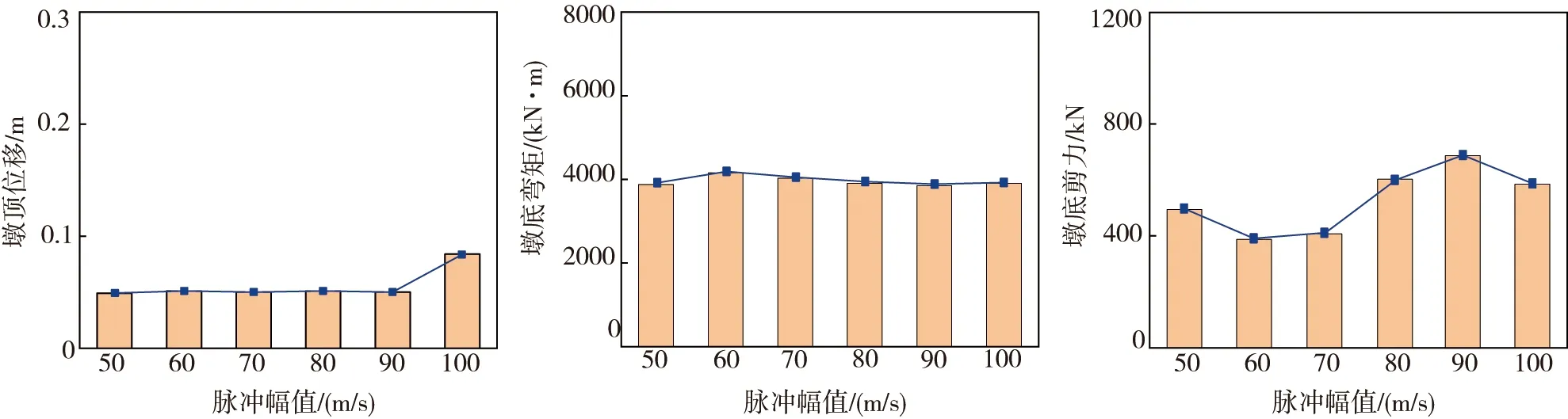
图8 开始出现破坏前结构内力响应Fig. 8 Structural internal force response before failure
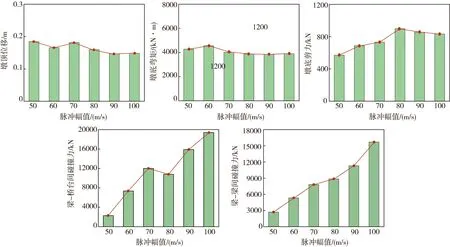
图9 不考虑单元失效时结构最大地震响应Fig. 9 Maximum seismic response of structure without considering unit failure
从表3与图8可以看出:不同脉冲幅值地震对桥梁地震响应影响较为明显。墩顶水平位移在Vp=50~90 cm/s时均在0.05 m附近,偏差较小,仅在Vp=100 cm/s时结果达到0.084 m。此外,墩底弯矩结果变化较小,Vp=60 cm/s时最大弯矩为4 160 kN·m,相较于平均值3 950 kN·m提高了5.3%。随着脉冲幅值的提高出现明显波动的是墩底剪力,其平均值为526 kN,最大值为687 kN,最小值为387 kN,波动幅度为±30%。
从表4与图9可以看出:脉冲幅值的大小与各响应结果存在着一定的相关性,特别是梁-梁和梁-桥台间的碰撞效应正比关系最为明显。罚函数法的理论指出:接触力(碰撞力)的大小与穿透深度和主表面刚度大小有关,故而提高脉冲幅值会加剧梁间的碰撞效应,从而消耗大量地震能量。
图10为Vp=60 cm/s和Vp=70 cm/s时梁-桥台和梁-梁间的碰撞力和相对位移时程曲线。从结果可以看出:当相对位移达到0.05 m时,即墩梁相对位移达到梁间伸缩缝间隙时,梁间会发生碰撞,Vp=70 cm/s时的碰撞次数和碰撞力的大小均要明显大于Vp=60 cm/s。但墩底弯矩变化依旧不明显,这与塑性铰区的特性有关,即墩底弯矩超过屈服弯矩后,桥墩进入塑性,塑性铰迅速增大,弯矩变化不明显。
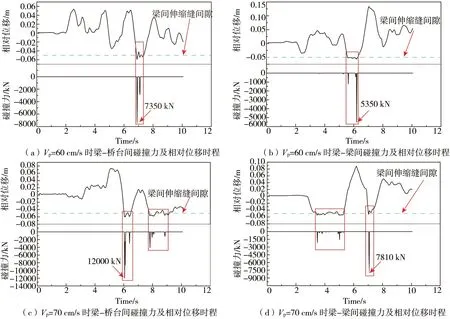
图10 不同脉冲幅值下梁-桥台间、梁-梁间碰撞力及相对位移时程Fig. 10 Time history of impact force and relative displacement between beams and abutments and beams under different pulse amplitudes
此外,根据桥梁开始出现单元失效的时间点T1来看:脉冲幅值的变化对破坏时间点的影响较小,仅在Vp=100 cm/s时出现较大偏差。
3.3 不同脉冲周期地震下倒塌过程及响应分析
对脉冲周期而言,现在还没有统一的计算方法,常用的有“零交法”、“峰点法”以及利用速度反应谱峰值对应的周期作为脉冲周期的Sv法,几种方法各有优劣。为了简单化,人为选择脉冲周期梯度依次为1.0、1.5、2.0、2.5和3.0 s进行人工脉冲地震动的合成,研究脉冲周期对简支梁桥的倒塌过程和地震响应的影响。
3.3.1 倒塌过程分析
不同脉冲周期地震作用下桥梁的倒塌模式主要是桥墩墩底损伤严重而引起的倒塌。为对比脉冲周期对简支梁桥倒塌过程的影响,选择不同工况下相同时刻桥墩损失情况进行分析,结果如图11所示。由于图11(c)和图11(d)两组工况在T=4 s时结构已明显破坏,便不再考虑4 s后的情况。
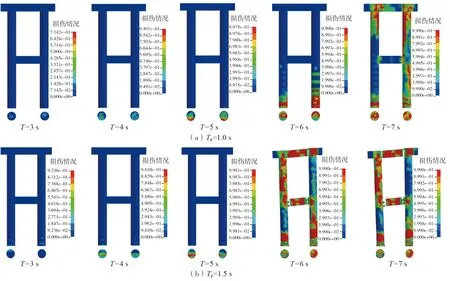
图11 不同脉冲周期地震作用下简支梁桥桥墩破坏过程Fig. 11 Destruction process of simply supported beam bridge pier under different pulse periods
从图11中可以看出不同脉冲周期地震作用下简支梁桥桥墩的损伤变化过程。当Tp=1.0 s和Tp=1.5 s,T≤5 s时桥墩并没有出现单元失效,仅墩底截面处出现一定程度的损伤,当T=6 s时开始出现明显差异。Tp=1.0 s时墩底受力变化剧烈,但桥墩整体结构依然完整;Tp=1.5 s时墩底混凝土出现大面积单元失效,并逐渐失去支撑能力,桥墩开始倒塌。与Tp=1.0 s和Tp=1.5 s相比,Tp=2.0 s和Tp=2.5 s的结果与之近似,区别在于桥墩开始出现破坏的时间更靠前。Tp=3.0 s时这种情况依然存在,T=4 s时桥墩已经出现严重破坏,但后续地震作用不断衰减,桥墩的破坏程度没有明显加剧。
3.3.2 动力响应分析
同样,为了研究脉冲周期与桥梁地震响应间的关系,分别提取地震作用下开始出现单元失效前的响应见表5与图12和不考虑单元失效的整个地震过程中的最大响应见表6与图13。
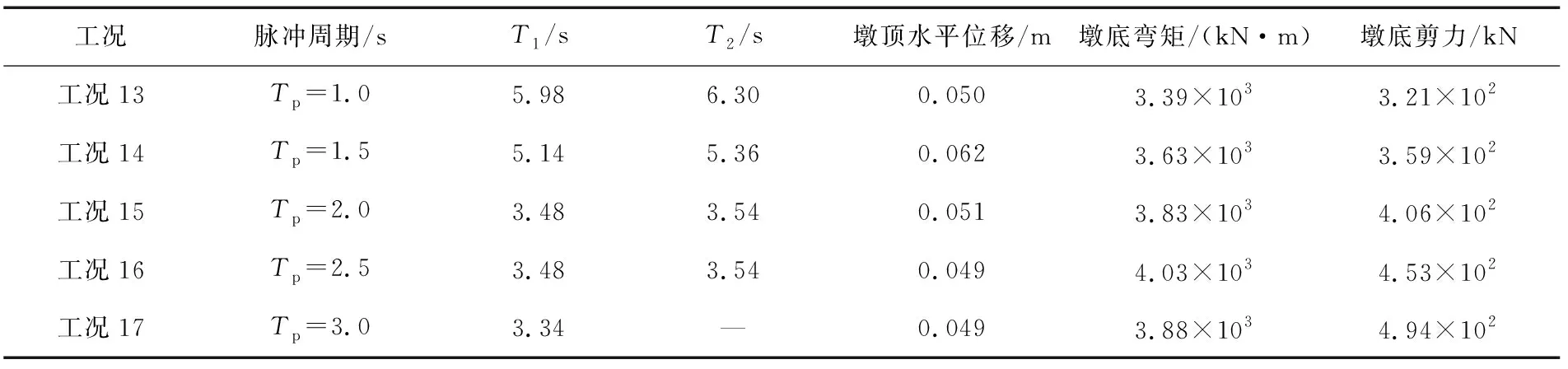
表5 开始出现单元失效前结构地震响应Table 5 Structural seismic response before unit failure

表6 不考虑单元失效时桥梁最大地震响应Table 6 Maximum seismic response of bridge without considering unit failure
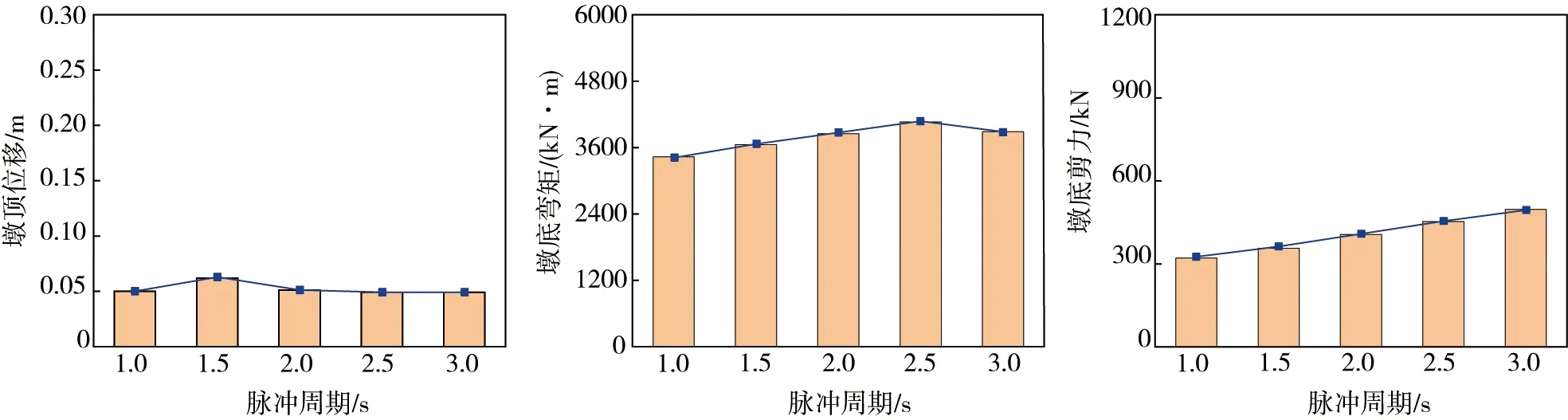
图12 开始出现破坏前结构内力响应Fig. 12 Structural internal force response before failure
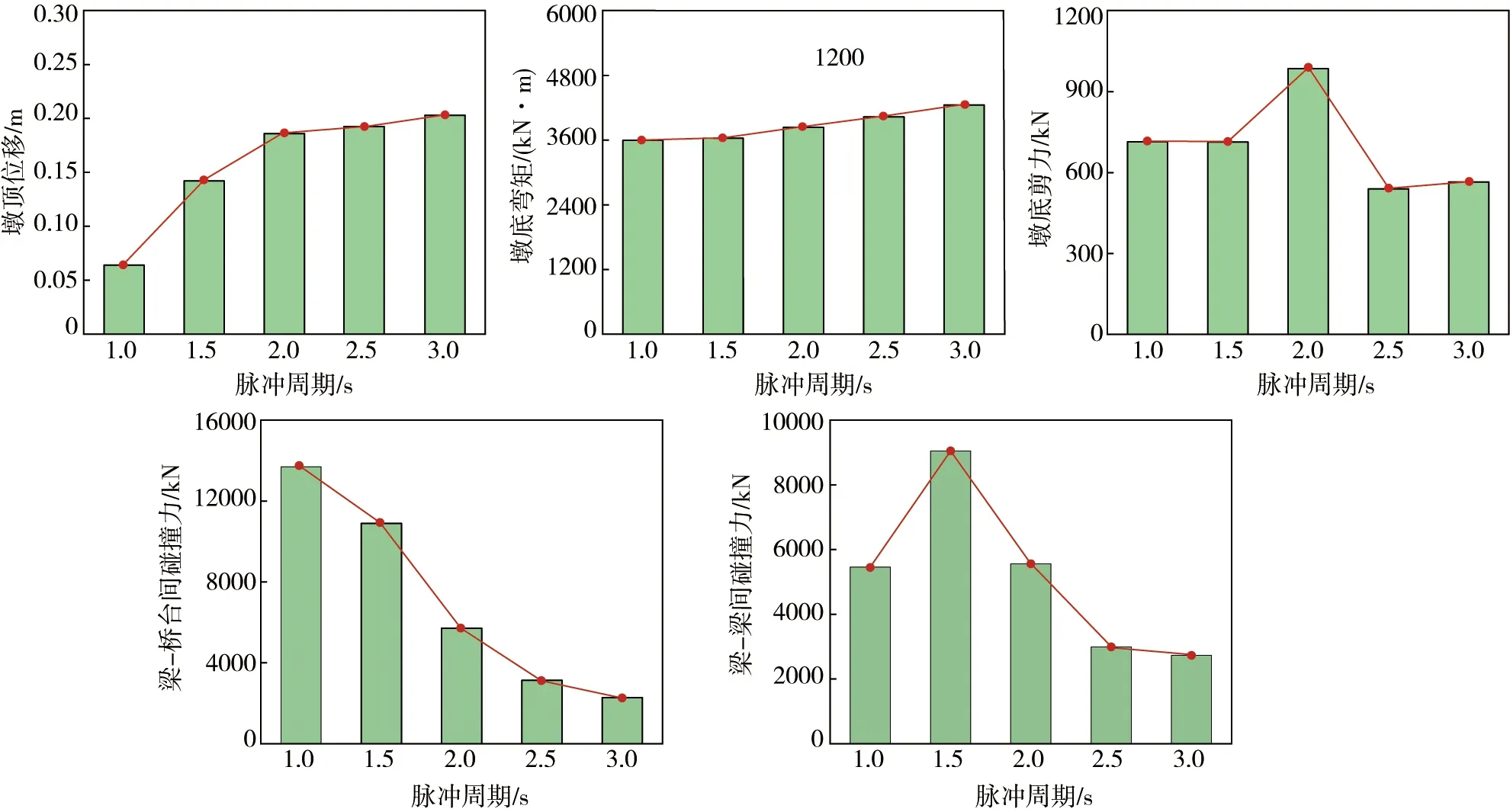
图13 不考虑单元失效时桥梁最大地震响应Fig. 13 Maximum seismic response of bridge without considering unit failure
从表5与图12可以看出:桥梁发生破坏前,桥墩的响应结果随脉冲周期的变化情况较为稳定,墩底剪力存在一定的增加趋势。Tp=2.5 s时墩底弯矩最大值为4 030 kN·m,相比平均值3 752 kN·m高出7.4%;Tp=1.5 s时墩顶水平位移取最大值为0.062 m,比平均值0.052 m高出近20%。
表6与图13为不考虑单元失效时整个地震过程中的最大响应结果。就桥墩而言,增大地震的脉冲周期并不会明显增大桥梁的的地震响应,这与地震波的频谱及结构自振情况有一定联系。从Tp=2.0 s结果来看:墩底剪力结果比Tp=1.0 s时高出38%,比Tp=2.5 s时多出82%,响应结果随着脉冲周期的增大呈现出先增大后减小的趋势。虽然墩底弯矩不断增加,但增加幅度较小,主要集中在平均值3 870 kN·m左右。脉冲周期较小时,水平位移也较小,但Tp=2.0 s时的水平位移已提高近两倍。相比之下,梁-桥台间的碰撞效应与脉冲周期的变化较为明显,脉冲周期越大,梁间碰撞效应越小。
此外,桥梁开始出现单元失效的时间点T1与脉冲周期的大小有密切联系。地震脉冲周期越小,开始出现损伤的时间点越靠近地震加速度峰值所在时间。由图5可以得到合成脉冲周期地震峰值所在时间点为t=4.86 s,考虑1 s的应力初始化,即在后处理结果中地震峰值对应时间点为5.86 s。计算不同脉冲周期工况下桥梁开始破坏的时间点与5.86 s的差值,分别为0.12、0.72、2.38、2.38和2.42 s,是依次增大的,这与脉冲地震的叠加合成有一定关联。由图10可知:脉冲周期的增大会导致加速度数值叠加的时间范围扩大,从而造成桥梁开始出现破坏的时间T1随脉冲周期变化而变化,这也说明了仅考虑脉冲幅值变化时T1的变化不明显。
3.4 地震作用下简支梁桥灾变过程总结
对表4和表6中关于简支梁桥开始破坏前墩底弯矩进行汇总得到图14。从图中可以看出:简支梁桥开始破坏前的墩底弯矩结果集中在一个固定值附近,并且有70%的结果分布在3 500 kN·m至4 000 kN·m之间,反映出桥墩开始出现破坏时的弯矩值与截面的承载能力有关,荷载的不同并非第一要素,这是符合客观规律的。故桥梁结构开始出现破坏的时间T1取决于最不利构件的截面承载能力小于荷载效应的时刻。
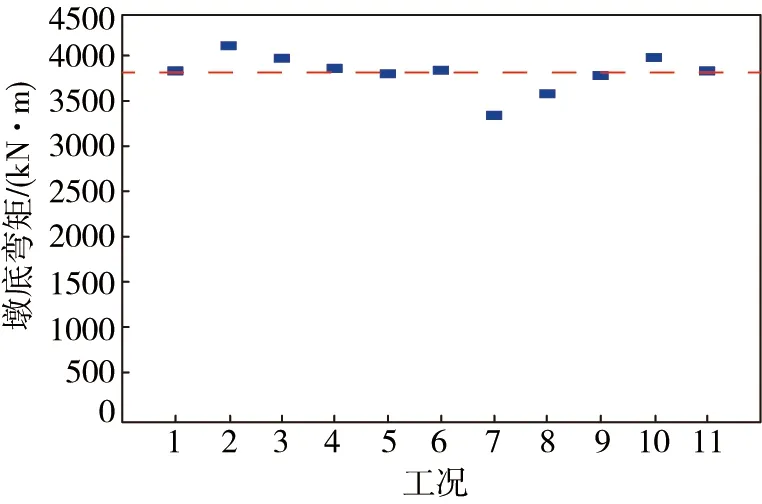
图14 开始破坏前墩底弯矩结果图
而桥梁倒塌时间T2的判定需要科学合理的倒塌标准,但局限于考虑的情况有限、算例较少和缺乏试验结果的对比等因素,文中仅通过计算结果,人为观察出现明显倒塌迹象的时间作为倒塌时间。
基于上述总结的地震作用下简支梁桥倒塌破坏过程,以及桥梁开始破坏的时间T1、桥梁倒塌的时间T2,参考美国联邦应急管理针对构件的性能水平以及受损程度划分的四个阶段,提出荷载作用情况与整体承载能力的变化如图15所示。
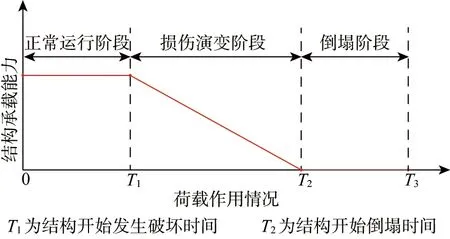
图15 结构承载能力随荷载作用情况变化
图15中按照荷载作用时间分为了正常运行阶段、损伤演变阶段以及倒塌阶段:当T
4 结论
基于LS-DYNA平台建立了简支梁桥的三维有限元模型,模拟了脉冲地震作用下简支梁桥的倒塌过程,研究了脉冲幅值和脉冲周期对简支梁桥倒塌过程和地震响应的影响,总结了地震作用下简支梁桥的灾变过程。主要结论如下:
1)脉冲幅值对简支梁桥的倒塌模式影响显著。当脉冲幅值Vp=70 cm/s时,墩底出现大量失效单元,从而导致桥墩倒塌。当脉冲幅值Vp=90 cm/s时,桥梁逐渐失去支撑造成桥梁整体倒塌。当脉冲幅值Vp=100 cm/s时,桥梁的破坏形式为墩梁相对位移过大而引起的落梁破坏。
2)脉冲幅值对桥梁位移响应影响较小,对内力响应和碰撞效应影响较大,增大脉冲幅值会加重梁间的碰撞效应,从而消耗大量地震能量。
3)改变脉冲周期对桥梁的位移和碰撞响应都有明显影响,位移响应随脉冲周期的增大而增大,梁间碰撞力则与之相反。此外,桥梁开始出现损伤的时间与脉冲周期的大小有关,脉冲周期越小,开始出现损伤的时间越靠近地震加速度峰值时刻。
4)桥梁结构开始出现破坏的时间与构件截面抗力和荷载效应的大小有关。脉冲地震作用下简支梁桥的倒塌大致表现为三个阶段:分别为正常运行阶段、损伤演变阶段和倒塌阶段。
