饱和地基中波阻板远场被动隔振的二维BEM-FEM耦合分析
2023-08-18朱超杰陈既学
时 刚,朱超杰,陈既学
(郑州大学 土木工程学院,河南 郑州 450001)
0 引言
进入21世纪,随着我国城市化进程的加速,交通拥挤等“城市病”频发。为解决城市交通拥堵问题,各大城市纷纷掀起了高架桥、地下隧道和轨道交通的建设高潮,给人们带来交通便利的同时也引发了一些负面问题,其中:轨道交通引起的环境振动污染问题备受关注。此外,工程施工(打桩和强夯等)和动力机械运行等也会产生环境振动污染。环境振动污染会影响到周边居民正常的生活,干扰精密仪器设备的运行[1],严重时还会危及建筑结构的安全。国际上已把振动污染列为“七大环境公害”之一,因此,振动污染的防治就成为当前各大城市急需解决的重要课题之一。
振动污染治理方法较多,其中:在地基中设置波阻屏障来切断振动传播途径是实际工程中的一种常用方法[2],工程中常用的连续屏障(空沟和填充沟)和非连续屏障(排孔和排桩)限于设置深度、施工难度和成本等问题,难以对对低频振动污染进行防治,此时,在振源或被保护结构下一定深度内设置波阻板(WIB)进行隔振是一种优选方案。SCHMID等[3]基于人工基岩理论最早提出了波阻板的概念,并采用BEM分析了波阻板主动和被动隔振问题;PEPLOW等[4]采用边界积分方程法计算分析了波阻板在二维双层地基中的主动隔振问题;高广运等[5-9]采用半解析BEM和模型试验方法分别研究了不同地基条件下(包括均质地基、层状地基、非均质地基以及饱和地基)波阻板的隔振问题;时刚等[10]采用BEM研究了均质地基中波阻板的远场被动隔振问题;针对轨道交通振动污染问题,高广运等[11-12]采用2.5维FEM分别研究了非均匀弹性地基和饱和地基条件下波阻板对列车诱发振动的隔振效果;CELEBI等[13]采用非线性2D-FEM研究了铁路道床和被保护建筑下方设置波阻板时的隔振问题,分析了列车运行速度对隔振效果的影响;陈洪运等[14]采用模型试验方法研究了高速铁路路堤中波阻板的减振效果;宋永山等[15]采用数值方法研究了准饱和地基上高铁列车运行诱发振动的波阻板隔振问题;此外,TAKEMIYA[16-17]提出了一种新型波阻板-蜂窝状波阻板,分析了其对高架桥交通振动的隔振效果;李志江等[18]采用FEM研究了实体波阻板和蜂窝状波阻板对高速铁路诱发环境振动的隔振效果;高盟等[19-21]和ZHANG等[20]提出一种新型波阻板系统-Duxseal-WIB,并采用现场试验方法研究了该隔振系统对竖向荷载和高速列车诱发振动的隔振效果。
上述文献主要研究了波阻板的主动隔振效果(WIB设置于振源下方),少数文献虽然也研究了波阻板的被动隔振问题(WIB设置在被保护结构下方),但仅限于单相介质的情况。针对饱和地基中波阻板对入射Rayleigh波的远场被动隔振问题,建立了饱和土半解析BEM-FEM耦合计算方法,推导了波阻板对入射Rayleigh波隔振的BEM-FEM耦合方程,在此基础上,计算分析了饱和地基中波阻板的远场被动隔振效果,初步探讨了组合式波阻板(由多种材料组成的波阻板)的隔振效果。
1 波阻板远场被动隔振的二维BEM-FEM耦合分析
当建筑物距振源较远时,振源产生弹性波中的体波衰减较快,此时Rayleigh波占主导,因此,屏障远场隔振通常简化为对入射Rayleigh波的隔振问题。为减小入射Rayleigh对建筑物的振动影响,可在地基一定深度处设置波阻板(WIB),如图1(a)所示。由于WIB对土层振动的屏蔽作用,从而使得WIB上方区域的振动大大减弱,从而对屏蔽区域内的被保护建筑产生隔振效果。

图1 WIB对入射Rayleigh波远场被动隔振的示意图Fig. 1 Passive vibration isolation by WIB
本文主要研究二维条件下饱和地基中波阻板远场被动隔振问题,采用饱和土半解析BEM-FEM耦合方法进行求解,其中,饱和土地基采用饱和土二维半解析BEM进行建模[22],而波阻板则采用FEM进行建模,通过饱和地基-波阻板交接面的相容条件和平衡条件将两部分模型耦合起来,这样就形成了饱和土二维半解析BEM-FEM耦合方法。特别是当波阻板由多种不同材料组成时(本文称为“组合式波阻板”),采用FEM对这种组合式波阻板进行建模非常适合,可以大大降低计算分析的难度。
1.1 饱和地基的二维半解析BEM方程
采用饱和土半解析BEM分析WIB远场隔振问题时,仅需要在饱和地基-波阻板交界面上划分边界单元,如图1(b)所示。当Rayleigh波入射到WIB表面时,由于WIB材料与周围土体材料的显著差异,从而对Rayleigh波产生散射作用,根据波场分解理论,饱和地基中的散射波波场的边界元方程可表示为[21]:
(1)
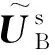
1.2 波阻板的FEM方程
WIB采用FEM进行建模,FEM有限元网格如图1(b)所示。WIB振动的FEM方程可表示为:
(2)
考虑稳态振动问题,为简化起见,省略e-iωt,并采用瑞利阻尼的形式,则WIB稳态振动的FEM方程可表示为:
(3)
式中:上标“~”表示稳态振动量的幅值,ω为振动圆频率,α和β分别为瑞利阻尼系数。
为表示方便起见,式(3)经整理后可表示成如下形式:
(4)
式中:Aij=(1-iωβ)Kij-(ω2+iωα)Mij。
1.3 饱和地基-波阻板交接面的相容和平衡条件
对于饱和地基-波阻板交接面,考虑到振动位移量级较小,不考虑交接面的相对滑移和脱开。网格划分时,饱和地基的边界元网格节点与WIB的有限元网格节点在交接面上一一对应。因此,饱和地基-波阻板交接面的连续性条件可表示为:
(5)
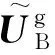
根据波动理论,地基中的总波场位移为散射波场位移和入射波场位移的相互叠加,有:
(6)
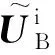
考虑WIB不透水的情况,根据总波场的分解方法,有:
(7)

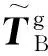
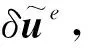
(8)

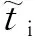
(9)
(10)
将式(9)和式(10)带入式(8),则可得:
(11)

(12)
对比式(12)和式(11)可得:
(13)
(14)
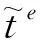
(15)
式中:Me为单元e的转换矩阵,可根据形函数按式(13)-式(14)计算得到。
按照上述思路,在全部饱和地基-波阻板交接面边界单元中计算Me,按照边界元节点所在位置进行组装,最终可得到整体转换矩阵Mg。
应当注意,由于WIB不透水,因此,饱和地基-波阻板交接面的平衡条件表示为:
(16)
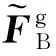
根据波场的叠加原理,饱和地基-波阻板交接面的平衡条件最终可表示为:
(17)
1.4 波阻板对入射Rayleigh波散射的半解析BEM-FEM耦合方程
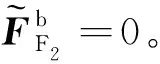
按照上述耦合方法,最终可得WIB对入射Rayleigh波远场隔振的半解析BEM-FEM耦合方程为:
(18)
式中:0为零子矩阵。
求解式(18)可得到饱和地基-波阻板交接面边界节点和WIB内部有限元节点对应的量。
为衡量WIB的隔振效果,定义竖向位移振幅衰减系数ARF:
(19)
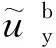
(20)
式中:x为地基表面计算点的坐标向量,H(x)和G(x)分别为边界元节点对“内点”的影响系数矩阵。
此外,为评价WIB的整体隔振效果,定义平均竖向位移振幅衰减系数AR如下[24]:
(21)
式中:l′为WIB上方的屏蔽区域宽度,在本文中,屏蔽区域宽度与WIB同宽,即l′=W。
2 程序验证
为验证本文所编制程序的正确性,与已有文献结果进行对比分析。当波阻板的埋置深度D→0时,波阻板远场隔振问题可等效为填充沟的远场隔振问题;此外,当n→0和ρf→0时,饱和地基就退化成弹性地基,可与弹性地基相应问题的解答进行对比验证。
算例1)采用文献[24]中填充沟对Rayleigh波隔振的算例进行验证。主要计算参数如下:地基土杨氏模量Es=46.12 MPa,泊松比νs=0.25,密度ρs=1 720 kg/m3;填充沟的杨氏模量Et=34.3Es,泊松比νt=0.25,密度ρt=1.37ρs。采用本文程序对该问题进行计算,对比计算结果如图2所示。由图可知:无论是填充沟的前方还是后方,除个别位置外,本文计算结果与文献结果相差很小,验证了本文算法的可靠性。

图2 计算结果对比(无量纲沟深1.0,沟宽0.4)Fig. 2 Comparison between present work and the algorithm of reference[24]
算例2)文献[22]建立了饱和土二维半解析BEM方法,分别采用文献[22]方法与本文BEM-FEM耦合方法对饱和地基中WIB的远场被动隔振问题进行计算,对比结果如图3所示。其中:饱和土地基的材料参数见表1。波阻板的埋深D=0.2λR,宽度W=4λR,厚度T=0.2λR;波阻板的剪切模量μwib=200μ,密度ρwib=2 400 kg/m3,泊松比νwib=0.22。

表1 饱和土地基的材料参数Table 1 Mechanical parameters of saturated soil
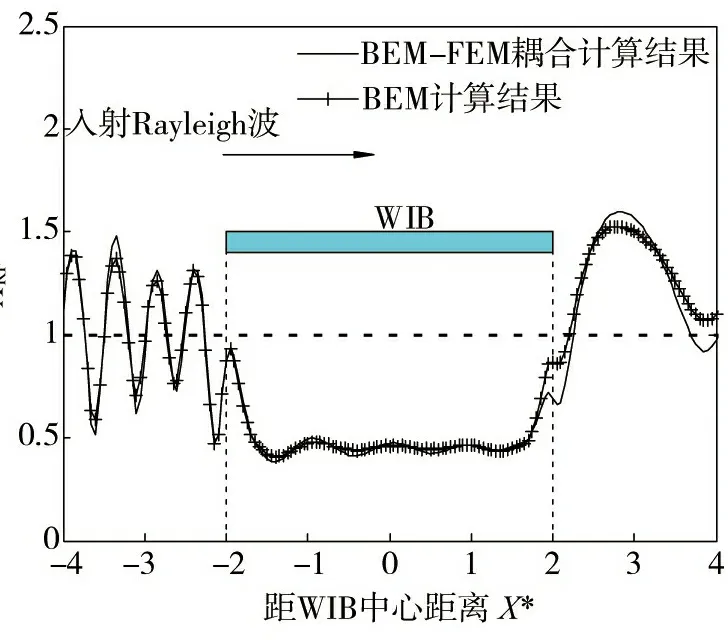
图3 本文算法与文献[22]算法的对比Fig. 3 Comparison between present work and the algorithm of reference[22]
由图3可知:采用文献[22]建立的饱和土半解析BEM计算波阻板的远场隔振效果与本文半解析BEM-FEM耦合算法的结果具有较好的一致性,表明本文算法是可靠的。
3 波阻板远场被动隔振效果分析
采用本文建立的饱和土半解析BEM-FEM耦合方法分析波阻板的远场被动隔振效果时,选取饱和地基的VR=100 m/s,并考虑对10 Hz的低频人工振动进行隔振,其中:Rayleigh波波长为λR=10 m。饱和地基的材料参数取表1的数值。
采用饱和地基的Rayleigh波波长λR作为无量纲化条件,其中:波阻板的无量纲埋深D*=D/λR,无量纲宽度W*=W/λR,无量纲厚度T*=T/λR。
本节考虑两种类型的波阻板:均质波阻板和组合式波阻板。基本分析工况为均质波阻板形式,波阻板的泊松比νwib=0.22,密度ρwib=2 400 kg/m3,剪切模量采用无量纲形式,有G*=μwib/μ;WIB其他计算参数见表2。对于组合式波阻板,波阻板几何参数与基本分析工况相同,仅考虑组成材料的不同。

表2 基本工况的计算参数Table 2 Parameters of a row of holes
本文研究采用单因素分析法,即考虑波阻板某一种参数的影响时,其他参数保持不变。
3.1 基准工况下均质波阻板的远场被动隔振效果
基本工况条件下(第2节算例2),均质波阻板对入射Rayleigh波的隔振效果如图3所示,其中:距WIB中心距离X*为无量纲量,定义为X*=x/λR。由图可知:当左侧入射的Rayleigh波传播到波阻板位置处,一部分Rayleigh波被波阻板反射回去并与入射波相互叠加,从而在波阻板前方产生振幅放大现象;在波阻板上方的地表处,由于波阻板的截频效应而降低了该范围内土层的振动,ARF在0.4左右,具有较好的隔振效果。WIB后方区域,ARF大于1,这表明一部分Rayleigh波绕过WIB后对地表产生较大的振动影响。此外,波阻板上方地表的振动屏蔽区域与波阻板设置范围基本吻合。
综上所述,在被保护建筑物下方一定深度处设置波阻板可有效降低被保护建筑的振动响应,有效屏蔽区域位于波阻板宽度范围内。
3.2 均质波阻板远场被动隔振的参数分析
参考相关文献研究,本文主要分析波阻板的埋置深度D、波阻板的宽度W和厚度T及其剪切模量μwib对隔振效果的影响规律,分析时采用单因素分析方法。
1)波阻板埋置深度D的影响
考虑波阻板埋置深度D影响时,WIB无量纲埋深D*分别取0.1~0.6,计算结果如图4-5所示。
由图4可知:当WIB埋置深度较小时,例如D*≤0.2,波阻板上方地表区域的隔振效果较好,且屏蔽区域内的竖向位移振幅衰减系数ARF变化较为平缓;随着埋深D*的增加(D*≥0.3时),波阻板上方屏蔽区域内ARF出现明显的波动起伏,表明振动波在半空间表面与波阻板之间产生复杂的反射现象;随着埋深D*进一步增大,屏蔽区域内的隔振效果急剧劣化,特别是当D*=0.6时,WIB完全失去隔振效果,更多的入射Rayleigh波通过地面与波阻板之间的区域透射过去。
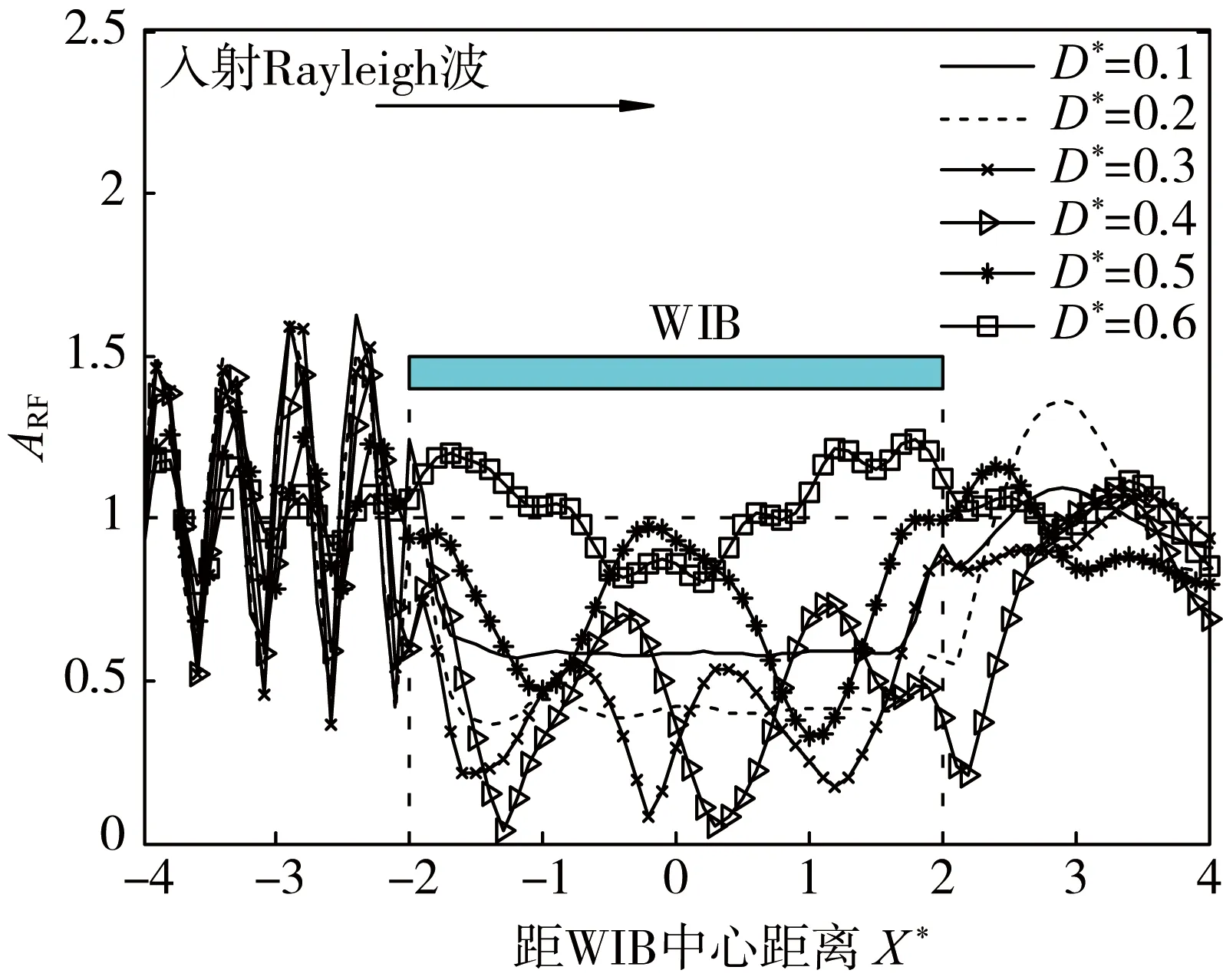
图4 WIB埋深D*不同时ARF随X*的变化曲线
由图5可知:WIB的平均竖向位移振幅衰减系数AR呈先减小后增大的现象,即随着埋深D*的增加,WIB上方屏蔽区域内的隔振效果先变好后逐渐劣化。在本文考虑的工况条件下,D*在0.2~0.4范围内时隔振效果最佳,过小的埋深并不能获得更好隔振效果,而过大的埋深导致WIB隔振失效。
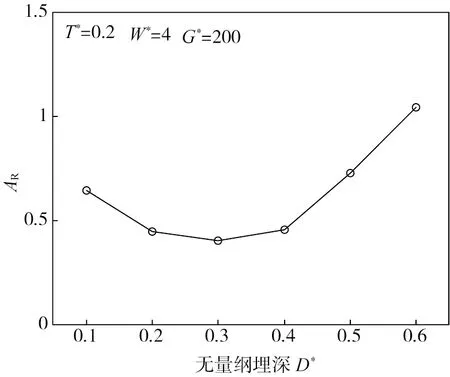
图5 WIB埋深不同时的平均竖向位移振幅衰减系数AR
综上所述,在饱和地基中采用WIB对入射Rayleigh波进行隔振时,为获得较好的隔振效果,建议埋深D*取0.2~0.4,过大埋深会导致隔振失效。
2)波阻板厚度T的影响
为分析波阻板厚度T对其隔振效果的影响,WIB无量纲厚度T*分别取0.1~0.5,计算结果如图6-7所示。
由图6可知:当WIB无量纲厚度T*较小时,波阻板上方地表区域的隔振效果较差;随着波阻板厚度T*的增大,屏蔽区域内的ARF逐渐减小,隔振效果逐渐变好。上述结果表明:增大波阻板厚度可有效提高波阻板的隔振效果,但WIB的工程建设费用和施工难度也随之增加。
amplitudeattenuationratioAR
由图7可知:WIB的平均竖向位移振幅衰减系数AR随厚度T*的增大呈单调递减趋势,即WIB上方屏蔽区域内的隔振效果随厚度T*的增加而逐渐变好。此外,当T*≥0.3后,WIB的隔振效果随厚度增加的幅度逐渐变小。
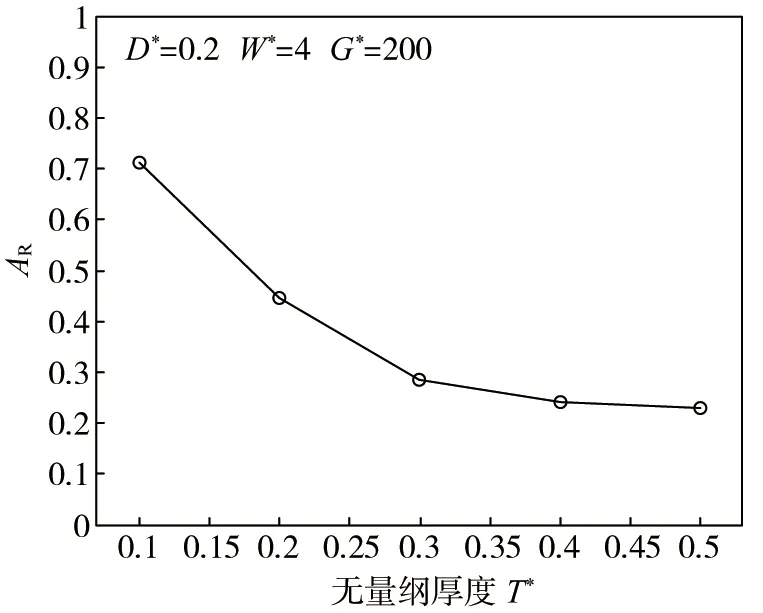
图7 WIB厚度T*不同时的平均竖向位移振幅衰减系数AR
综上所述,在饱和地基中采用WIB对入射Rayleigh波进行隔振时,过大的厚度虽然能够取得更好的隔振效果,但考虑到成本及施工等问题,建议WIB厚度T*取0.2~0.3。
3)波阻板宽度W的影响
考虑波阻板宽度W的影响时,波阻板无量纲宽度W*分别取1.0~8.0,计算结果如图8-9所示。
由图8可知:WIB的宽度W*对屏蔽区域内的隔振效果影响相对较小;屏蔽区域中间位置附近的ARF基本相同,屏蔽区域边缘(WIB边缘区域上方地面)处的ARF稍有不同。此外,地面屏蔽区域的范围与WIB宽度基本对应,WIB的宽度W*越大,地面屏蔽区域范围就越大。
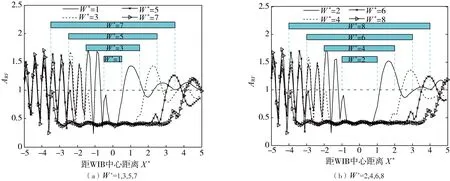
图8 WIB宽度W*不同时ARF随X*的变化曲线Fig. 8 Graph of ARF of WIB for different W*
由图9可知:除WIB宽度较小的情况(W*=1)外,WIB的宽度W*对屏蔽区域的平均隔振效果影响很小。
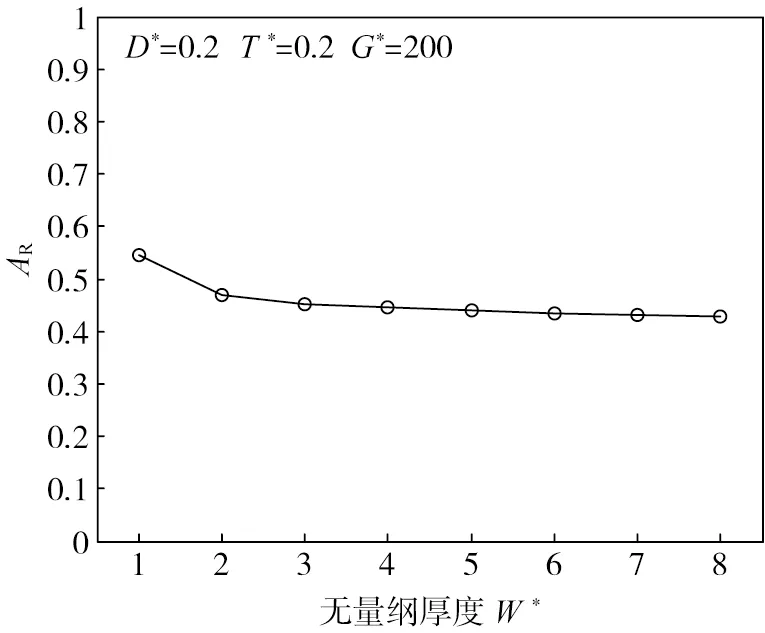
图9 WIB宽度W*不同时的平均竖向位移振幅衰减系数ARFig. 9 Effect ofW*on the average vertical displacement amplitude attenuation ratioAR
综上所述,实际工程设计时,建议根据被保护建筑的平面尺寸来确定WIB宽度,并使被保护建筑位于波阻板宽度范围内,过大的宽度并不会带更好的隔振效果。
4)波阻板剪切模量μwib的影响
考虑波阻板剪切模量μwib的影响时,WIB无量纲剪切模量G*分别取2、20、50、100、200、500和1000,计算结果如图10-11所示。
由图10可知:当波阻板无量纲剪切模量G*较小(G*=2)时,波阻板上方地表区域内的隔振效果相对较差,ARF大约在0.75左右;随着波阻板无量纲剪切模量G*的增加,WIB的隔振效果逐渐提升。
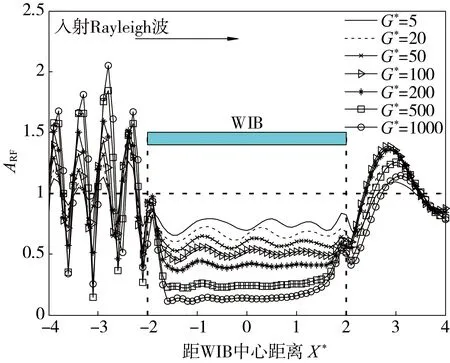
图10 WIB剪切模量G*不同时ARF随X*的变化曲线
由图11可知:WIB的平均竖向位移振幅衰减系数AR随无量纲剪切模量G*的增大呈单调递减趋势,即WIB上方屏蔽区域内的隔振效果随G*的增加而逐渐变好。
综上所述,实际工程设计时,建议提高波阻板的剪切模量μwib来提高其隔振效果,可在成本增加不大的情况下获得更优的隔振效果。
3.3 组合式波阻板的远场被动隔振分析
常用的波阻板多采用一种材料进行制作,隔振体系的设计也较为单一。马强等[25]基于功能梯度材料提出一种新型WIB-梯度波阻板,使波阻板的可设计性大大提高。然而在实际工程中,功能梯度材料制作较复杂,难以推广,将几种不同材料组合在一起制作波阻板则较容易实现,但目前尚未有学者进行相关研究。本节初步探讨采用两种不同材料制作的组合式WIB,分析不同组合方式对其隔振效果的影响规律,为新型波阻板研发提供参考。
1)水平层状组合式WIB的隔振效果
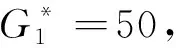

图12 不同形式的水平层状组合式WIB的示意图Fig. 12 Schematic of different layered WIB
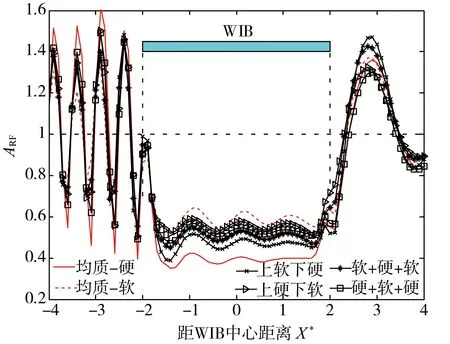
图13 不同水平层状组合式WIB的ARF随X*变化曲线Fig. 13 Graph of ARF for different layered WIB
由图13可知:尽管不同形式组合式WIB的两种组成材料比例相同,但其隔振效果存在较大差异:上软下硬形式的组合式WIB如图12(b)所示,隔振效果要好于其他三种;上硬下软形式的组合式WIB如图12(a)所示,隔振效果最差,这与功能梯度波阻板的规律基本吻合[25]。此外,与同等厚度均质材料的波阻板相比,层状WIB隔振效果好于软质材料(材料1)的波阻板而劣于硬质材料(材料2)的波阻板。
因此,在实际工程中进行波阻板设计和施工时,可根据实际工程需要采用水平层状组合式WIB以降低工程造价,并建议采用上软下硬形式来构建组合式波阻板。
2)水平分区组合式WIB的隔振效果
考虑到被保护建筑不同位置的隔振要求不同,可采用水平分区组合式WIB形式,如图14所示。其中:除不同区域的材料不同外,其他条件与水平层状组合式WIB相同,此处不再赘述。

图14 不同形式的水平分区组合式WIB的示意图Fig. 14 Schematic of combined WIB with different horizontal partitioning
由图15可知:水平分区组合式WIB的ARF呈现出明显的规律性:屏蔽区域内地表ARF呈波动起伏状分布,且与下方WIB材料特性相对应,例如:硬质材料分区上方地表的ARF值与硬质均匀材料WIB对应量基本相等,仅在不同材料分界处存在过渡。
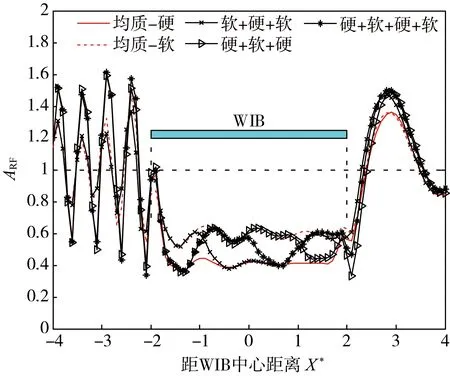
图15 不同水平分区组合式WIB的ARF随X*变化曲线Fig. 15 Graph of ARF for different combined WIB with different horizontal partitioning
根据上述分析,实际工程设计时,可根据被保护建筑的实际需求对波阻板进行分区设置,在获得较好隔振效果的同时降低工程造价。
4 结论
1)饱和地基中,在被保护建筑下方一定深度设置波阻板可有效降低由入射Rayleigh波引起的地表竖向振动,获得较好的隔振效果;地表屏蔽区域范围与WIB设置范围基本吻合。
2)在饱和地基中采用波阻板对入射Rayleigh波进行隔振时,为获得较好的隔振效果,建议WIB埋深D*取0.2~0.4λR;WIB的隔振效果随厚度增大而增加,但考虑到成本等问题,建议WIB厚度T*取0.2~0.3λR;WIB宽度对隔振效果影响微弱,建议根据被保护建筑的尺寸来确定合适的WIB宽度。
3)波阻板的隔振效果随其剪切模量的增大逐渐提高,实际工程设计时,通过提高WIB的剪切模量来提高其隔振效果,可在成本增加不大的情况下获得更优的隔振效果。
4)波阻板在竖向由多种材料组成时,建议采用上软下硬方式构建波阻板以获得更好的隔振效果;而对于水平分区组合式波阻板,地表隔振效果与其下方波阻板的材料性质相对应,实际工程中可根据振动控制要求的不同构建多种材料分区的组合式波阻板,使波阻板更具有可设计性。
