“线段图”的运用策略探究
2023-08-12张勇
张勇


【摘 要】“画图策略”是解决问题时常用的一种数学方法,是数形结合思想的具体体现。在教学中,教师经常会运用画图策略来帮助学生理解题意,但很少有学生会主动应用画图策略来帮助自己解决难题。也正是因为学生对画图策略缺少一定的意识,或感觉存在一定的困难,这才需要教师在平时的教学中有意识地引导和培养。
【关键词】教学策略 线段图 数形结合 数量关系
笔者在一次教研活动中同时学习了三位青年教师执教的苏教版数学四年级下册“解决问题的策略”一课,对“线段图”这一策略的教学颇有感触。
一、课中实践
片段一:画线段图
张老师在简单介绍集邮这一高雅艺术之后直接呈现例题,询问学生想到用什么方法,学生异口同声:画线段图。教师引导学生独立尝试画线段图之后精心挑选了两幅作品进行展示,让学生寻找相同点和不同点。在此过程中,教师相机将课前已经制作好的线段图进行板贴。
唐老师在学生集体读题之后,让学生集体口述线段图的画图步骤,教师相机出示课件,以此教学生画线段图。
马老师在读完例题后,简单提示学生自己独立画图,然后出示三份学生的作品,让其他学生分别找找三幅作品的亮点和不足,接下来则带领学生集体作图并修正自己的作品。
片段二:“读”线段图
对于“读”懂线段图这一环节,三位教师不谋而合地采取了同一教学策略:先在课件中隐去苏教版数学四年级下册P48例题1中的所有文字信息,只给学生观察所画出的线段图,让学生尝试复述例题中的条件和问题。从三节课中学生的反应可以看出,学生对于“读”线段图基本不存在困难。
片段三:用线段图
“读”完线段图后,三位教师采取的教学方法都是先引导学生尝试独立思考自己解决例题中的问题,随后进行充分的交流互动。
张老师的课堂上有学生汇报:
72÷2=36(枚)
小春:36+12=48(枚)
小宁:36-12=24(枚)
笔者观察到张老师在听完学生提出这一方法后脸上满是诧异和不解,课堂也陷入了短暂的停滞,张老师思考后说:“这种方法对吗?”
一个学生举手答道:不对,我们可以这样想,假设小春有48枚邮票,小宁有24枚,那么小春就比小宁少24枚邮票,可是题中告诉的是小春比小宁少12枚。
此环节到这里就结束了。
唐老师在学生出现同样方法之后处理如下。
师:同学们,我们先不着急评判这个同学的方法,老师这里有另外一个问题想问大家:“如果唐老师有8个苹果,这个女生有4个苹果,怎样让我们的苹果数量一样多呢?”
大部分学生能够很快答出老师应该分给女生2个苹果。
师:这个答案是怎么得来的呢?
从学生的自由回答中可以知道,学生是明白老师只需要把自己多出的4个的一半的数量分给女生,两人就能变得同样多了。
紧接着,唐老师再让全班学生进行思考、分析上面学生提出的先“÷2”的那个方法是否正确,从课堂效果可看出,部分学生能够将刚刚教师列举的苹果例子获得的经验迁移到这道题目上,得出:小春只需要把自己比小宁多出的12枚邮票拿出一半,即6枚分给小宁就可以了。学生得出此结论后,唐老师利用课件将这种方法的详细解答过程进行了展示及再次讲解。(见图1)
马老师的处理方法如下。
师:你们认为这种方法对吗?为什么呢?
生1:我认为不对,把48和24两个答案代入题中进行检验得到小春比小宁多24枚邮票,并非题目中所给的12枚。
师:那你觉得应该怎么做呢?
生1:我是这样想的,先用72÷2=36(枚),如果两人邮票同样多,小宁和小春每个人都应有36枚邮票。题目中提到小春比小宁多12枚,那么我们就可以用36+6=42(枚),这是小春的邮票枚数,然后再用36-6=30(枚)求出小宁的邮票枚数。
师:你的6怎么来的呢?
生1:12÷2=6(枚),小春比小宁多12枚,那么小春只需要把自己比小宁多出的12枚中的一半,即6枚给小宁就可以让两个人变得同样多。
接着,马老师将生1的方法板书到了黑板。
二、课后反思
(一)“线段图”在学习中的重要“地位”
纵观苏教版12册小学数学教材编者设计的“线段图”的相关教学内容,仔细分析可看到,教材是先用色块“遮盖”具体的数量,再用色块来统括大数据的数量,最后教材才编排了用线段来表示数量的多少及数量之间的关系,这一设计充分体现了苏教版数学教材在进行“线段图”这一内容编排时考虑到了由易到难、由具体到抽象。
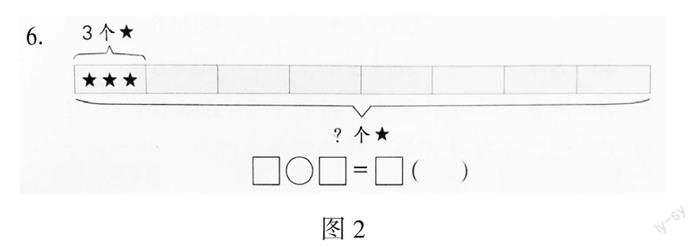
(1)用色块“遮盖”数量及关系:二年级上册“表内乘除法的练习”(见图2)一课是苏教版数学教材第一次涉及借助色块表示数量及关系。
此题意在引导学生发现问题的本质:“求 8 个 3 相加的和是多少?”这道题里的色块“遮盖”了具体的数量,学生在自己计算后可以通过数数的方法验证自己求出的色块遮盖住的五角星个数是否正确。
(2)用色块概括数量及关系:苏教版数学教材里第二次出现色块图是在二年级下册的“两、三位數的加法和减法”(见图3)一课。
这里用蓝色色块表示鸭蛋的数量,用黄色表示鸡蛋的数量,而且这两种颜色色块所表示的具体数量都比较多,无法运用数数的方法,因此这里的色块更具有概括数量多少的作用。学生在解题的过程中需要借助侧旁的文字描述与两种不同颜色色块的长短来分析、理解鸭蛋和鸡蛋两种数量间的关系。
(3)用线段图表示数量多少及数量关系:苏教版数学教材里第一次呈现出具体的线段图模型是在三年级上学期的“从条件想起”第一课时(图略)。
这是教材第一次使用比较简单、易懂的线段图来表示题中的条件及问题,让学生根据题中所给的条件完成线段图并借助线段图去理解、掌握、体会从条件出发分析题中的数量关系进而寻找相应的解题方法的数学策略。
(4)苏教版数学三年级下册“解决问题的策略”一课(图略)则是引导学生依据具体情境中的相关信息补全线段图,然后借助所补画出的线段图体会从问题出发分析题中的数量关系的解题策略。
(5)苏教版数学四年级下册“解决问题的策略”(见图4),则是让学生根据实际的具体问题补全题中线段图所缺的信息,然后再根据补全的线段图寻找到题中的数量关系进而找到解题的突破口,梳理出解决实际问题的思路。
在后续的苏教版数学五、六年级的教学中,也设计了很多借助线段图来分析题意、解决问题的实际问题。
纵观整个苏教版数学教材,我们可以发现,“线段图”这一教学内容在小学数学中占有举足轻重的地位。
(二)“线段图”在学习中的重要“优势”
线段图是一种解决数学问题较为常用的解题策略,它能帮助学生从形象思维较为顺利地过渡到抽象思维。线段图的最大优势在于化抽象为具体,通过线段图把题目中蕴含的较为抽象的数量关系用形象、直观的方式表达出来,从而引导学生将自己对概念的相关认识重新进行认知、内化,启发他们从完整的、形象的线段图中寻找到题目中所蕴含的数量关系,从而更高效地解决问题。另外,借助线段图,能让学生体会到以数化形、以形换数的思想,进而发展其思维品质。
那么,在实际的一线数学教学中,教师又该如何发挥线段图自带的这些优势呢?教师应先耐心引导学生将题目中的文字及其他信息用线段图进行具体呈现,接着引导学生借助线段图仔细分析每一部分所代表的意义和蕴含的数量之间的关系,寻找题目中所有信息所蕴含的相互联系,并以此建构起数学条件与问题之间所具备的数量关系模型,借此探索出较为适切的解决问题的思路。
如本课例题中的信息较为抽象,学生一时无法清楚地厘清题目中小宁和小春邮票枚数的内在联系,这时教师就可以相机引导学生利用画线段图的方法来表示题中的相关条件和问题,加深对题目的理解,然后仔细分析所画的线段图,就可发现小春、小宁邮票枚数之间存在的较为清晰的数量关系了。(见图5)
(三)“线段图”在学习中的重要“实力”
从三节课的课堂反馈中可以看到,绝大部分学生都能借助分析线段图快速地寻找到解决问题的突破口。
有的学生想到,先将小春比小宁多出的12枚邮票去掉,用72-12=60(枚)即得到原来小宁邮票枚数的两倍,然后再分别计算出小宁和小春各自的邮票数。
有的学生想到,先将小宁的线段图补画一段小春比小宁多的12枚,用72+12=84(枚)得到原来小春邮票枚数的两倍,再依次算出小春、小宁的邮票数。
由此可见,线段图的“实力”确实非凡。
如果授课教师能够在有学生出现“72÷2=36(枚) 小春:36+12=48(枚) 小宁:36-12=24(枚) ”这一错误方法后,像唐老师教学时一样先举出一个贴近学生生活实际的例子,让学生理解要使得两人同样多只需要把多出来的一半分给另外一个人,以此唤起学生的生活经验,然后再借助本节课学生需要学习和掌握的策略画线段图进行动画演示(见图6、7、8),让学生能够直观地感受到取其中的一半才能够进行均分,那么学习效果就会更好。
线段图是一种比较直观的解决问题的策略,它也是学生从具体、形象的思维过渡到抽象的逻辑思维的载体。在日常教学過程中,教师应先准确地把握学生的学情,然后根据具体的数学问题的特征,引导学生依次通过画图、分析来解决问题,同时引导学生在数与形、文与图之间相互转化。唯有此,学生在解决实际问题时方能得心应手,数学学习也才能兴致更浓、信心更足。
