基于Isomap-MPA-LSSVM 软测量模型的PVC聚合过程转化率预测

唐海红　张凯

关键词：自动控制技术其他学科;PVC聚合过程;软测量;等度量映射;海洋捕食者算法;最小二乘支持向量机

中图分类号：TP273;TQ325.3 文献标识码：A DOI： 10.7535/hbgykj.2023yx01003

在复杂的化学工业中，聚氯乙烯（polyvinylchloride，PVC）树脂在国民经济建设中占有非常重要的地位，由于本身具有良好的机械性能、耐腐蚀性和不易燃烧等特性，广泛用于工业、建筑、日常用品等领域[1]。PVC 聚合方式主要有悬浮法、溶液法、乳液法和本体法等[2]，本文是以悬浮法作为研究背景，进行理论方法和应用研究。PVC是以氯乙烯单体（vinyl chloride monomer，VCM）为原料聚合而成的热塑性聚合物。传统的VCM 转化率小于85%。不同的VCM 转化率对PVC的分子量、孔隙率、增塑剂吸收率等质量指标有很大影响[3]。因此，VCM转化率的实时监测在实际生产中非常重要。但在复杂的工业过程中，受现场条件的限制和缺乏昂贵的精密检测设备等，很难实时获取VCM 转化率，从而无法直接对质量形成闭环控制[4]。软测量技术的应用能够解决工业过程中难以测量的过程变量，通过建立软测量模型以实现VCM 转化率的实时预测和监控，对提高PVC产品质量有重要意义。软测量是用非线性数据进行驱动的技术，由于化工过程的复杂性，基于物理或化学平衡原理的精确表达式很难建立，而如今伴随着数据的大量保存，使得数据驱动的方法能够有效解决现实中的非线性问题[5]。数据驱动的软测量方法更灵活、更便宜、响应更快。

由于噪声数据的影响，以及数据本身之间也存在一定的共线性，因此，对工业过程收集的原始数据预处理至关重要，一些预处理方法被提出，如主成分分析（principal component analysis，PCA）[6]、核主成分分析（kernel principal component analysis，KPCA）[7]、多维尺度变换法（multi dimension scaling，MDS）[8]、等度量映射（isometric mapping，Isomap）[9]等。其中PCA 和MDS属于线性降维方法，存在局限性，不适合处理复杂的化工过程非线性数据，KPCA 是在PCA 基础上加入核函数思想的降维方法，但会丢失原始数据中的局部特征信息，降低原始数据该有的特性，而Isomap是在MDS基础上改进的，通过求测地距离的方式来计算数据间的距离，非常适合处理非线性数据，因此，本文采用Isomap特征提取方法，对收集的原始数据进行预处理。

目前，在数据驱动的建模方法中，人工神经网络（artificial neural network，ANN）[10-11]是常用的一类，但其收敛速度慢、全局寻优能力差，预测误差大。相较于ANN，支持向量机（support vector machine，SVM）[12-13]运算量小，收敛速度较快，而最小二乘支持向量机（least squares support vector machine，LSSVM）[14-15]是在SVM 基础上进行改进，将二次优化问题转化为线性方程组求解，简化求解问题，速度显著提升。因此，本文用LSSVM 建立软测量模型，而LSSVM 中参数值的选取直接影响模型的预测精度。SONG等[16]采用粒子群算法优化的LSSVM 对水下滑翔机能耗進行预测。LI等[17]将改进的鸟群算法优化LSSVM 来预测锂离子电池剩余寿命，从而提高了电池储能系统的安全性和可靠性。ZENG等[18]采用鲸鱼优化算法寻找LSSVM 合适的控制参数，来预测边坡安全系数。上述研究通过不同算法优化LSSVM 都取得了不错的效果。本文拟采用一种新颖算法：海洋捕食者算法（marine predators algorithm，MPA）。该算法具有独特的搜索方式以及良好的记忆功能，易于跳出局部最优，拥有很强的寻优能力，因此被广泛用于优化各种模型[19-21]。

本文以PVC聚合过程为研究背景，收集聚合过程中易于测量并与VCM 转化率相关的变量，作为辅助数据。为了消除数据间的共线性，降低模型复杂度，对收集的辅助数据以Isomap做降维处理，将处理后的数据作为模型输入，再通过MPA 优化LSSVM 模型，建立Isomap-MPA-LSSVM 软测量模型。相较于其他模型，本文提出的模型对VCM转化率的预测精度明显提升，可以满足工业指标的精确要求。

1 PVC聚合过程

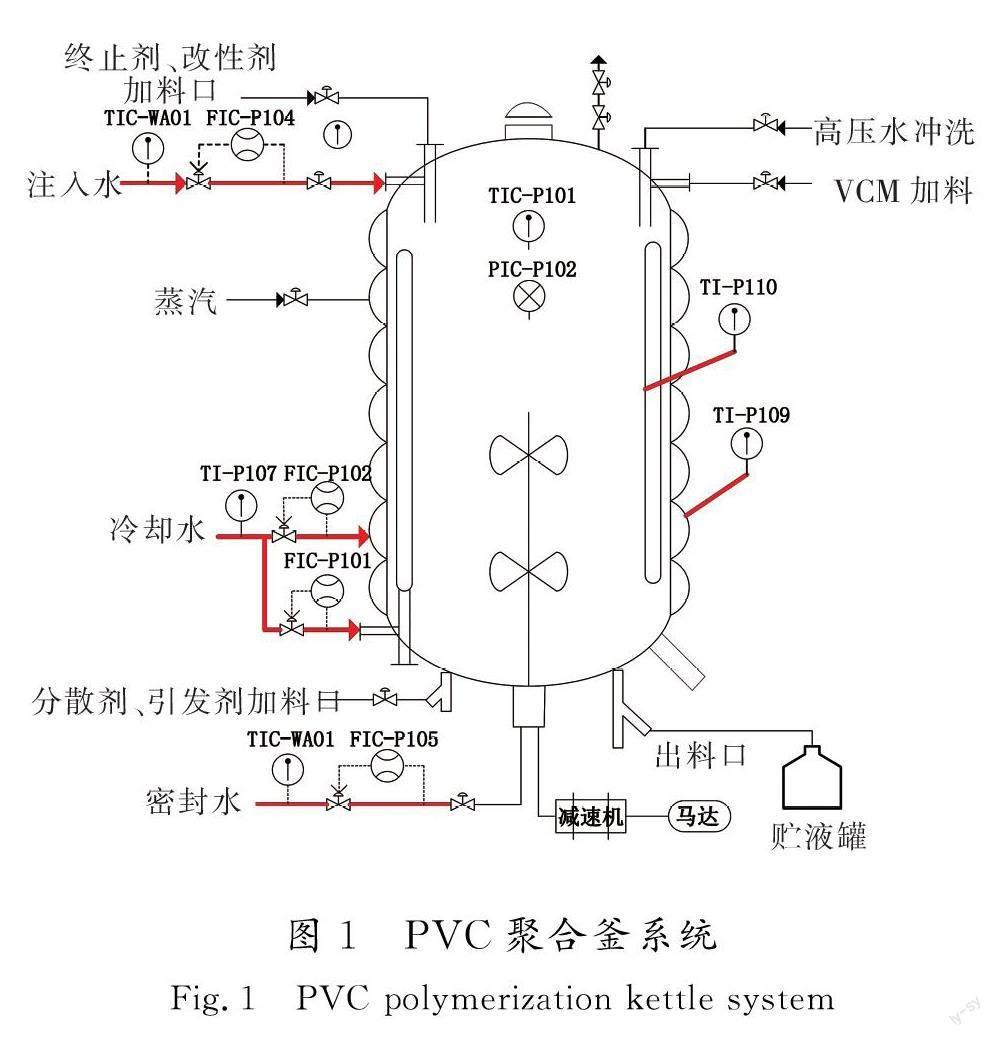
以聚合釜为反应装置，水为介质，依次加入各种原料和助剂，并在搅拌的作用下分散成小液滴。通过夹套热水使釜内物料温度升至预定值，最后加入引发剂进行聚合。在反应中，通过不断向反应釜的夹套和挡板通入冷却水移出反应热[22]。当VCM的转化率达到一定时，且出现一个适当的压降，加入终止剂结束反应出料[23]。PVC 聚合釜系统如图1所示。

本文提出了一种Isomap-MPA-LSSVM 软测量模型来预测VCM 转化率。软测量技术是通过容易测量的辅助变量构造数学映射估计无法直接测量的主导变量。相较于传统的传感器，软测量建模的方式不受实验环境和设备影响，只需对收集的数据进行研究，本质是软件编程的过程，因此更加的灵活方便。

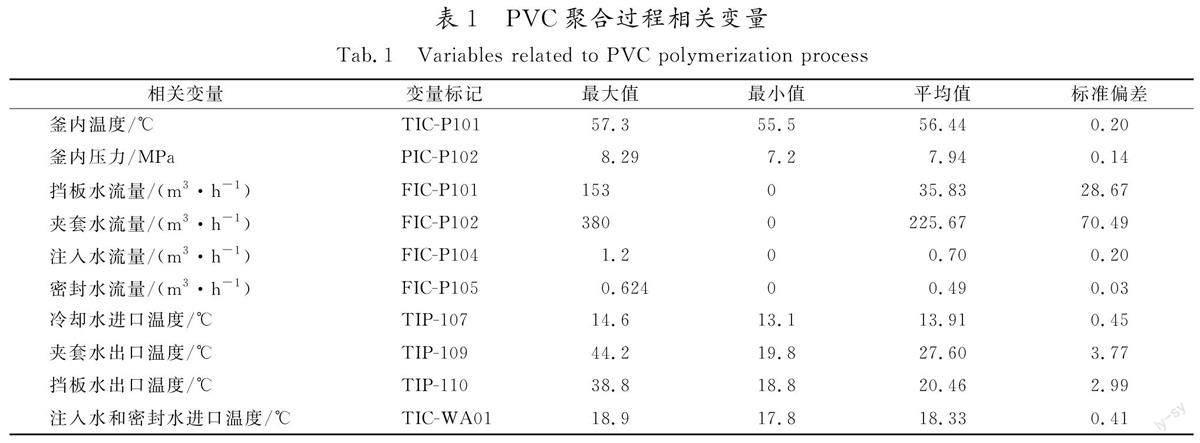
根据聚合釜工艺过程中采样的数据进行分析，确定了10个过程变量与VCM 转化率最为相关，作为建模的辅助变量。变量的具体信息如表1所示。

2 算法及主要计算过程

2.1 等度量映射

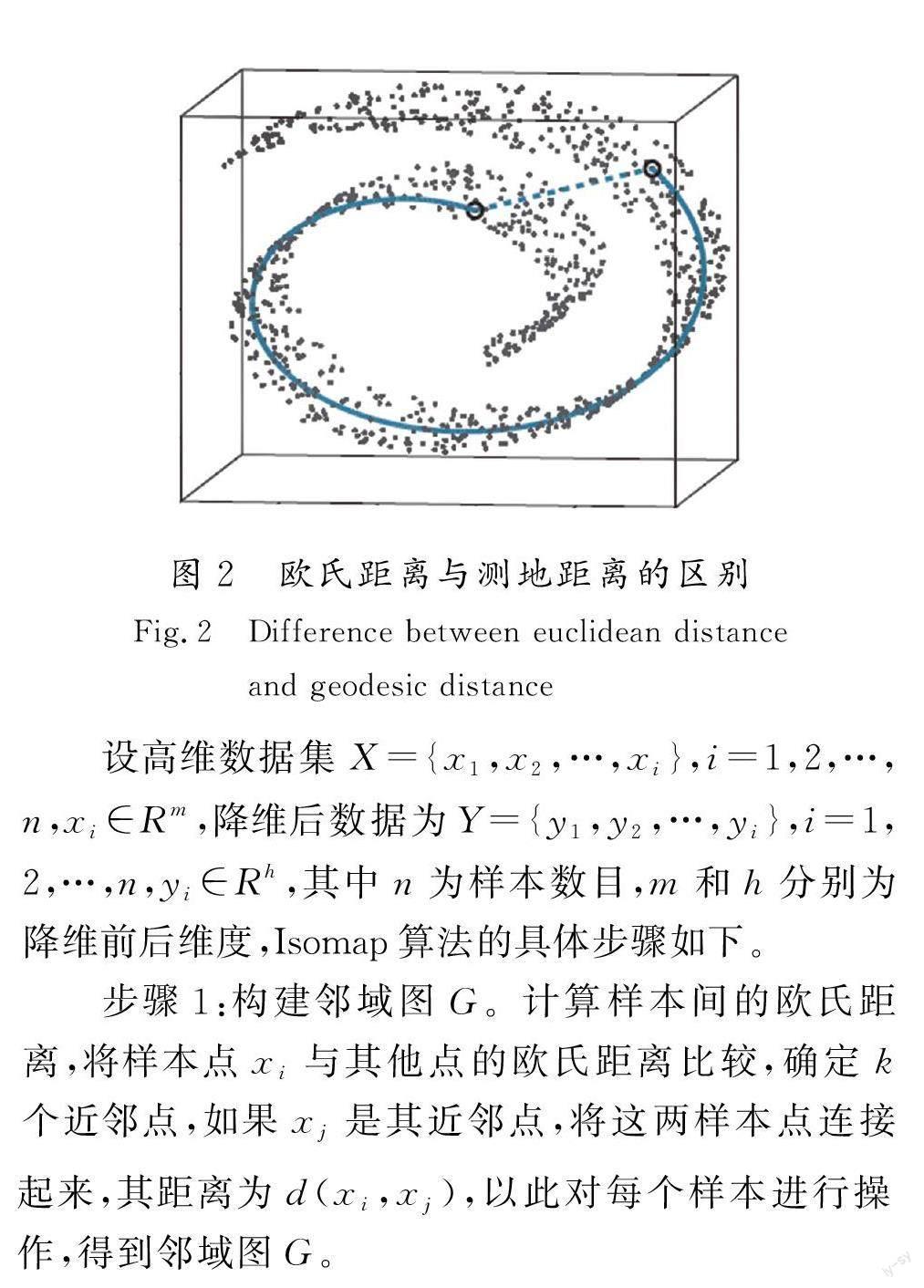
等度量映射（Isomap）算法是在MDS基础上改进的一种特征提取方法[24]，将高维数据映射到低维空间中，使数据在低维空间的距离与原本的高维空间近似，与MDS不同之处在于求数据点间的距离矩阵。在MDS中，数据被定义在欧氏空间中，通过求欧氏距离来判别数据之间的距离，然而在实际情况中，收集的非线性数据并不可能分布在欧氏空间中，而极大可能分布在一个流形体中，在Isomap算法中，通过这种流形体求解数据间的测地距离，更加反映数据点间的真实距离。以一个“瑞士卷”的流形体为例，数据分布在其上，如图2所示，当计算两点间的距离时，蓝色实线为两点的测地距离，即真实距离，而蓝色虚线是两点间的直线距离，即欧氏距离。可以表明，在高维空间下，计算数据间的距离不能通过简单的直线距离，而应采用测地距离更能真实反映数据间的内在联系。

3.2 仿真实验

以美国BFG公司的4万t/a PVC 生产装置的聚合工序为技术支持，对其过程进行了分析，得到了温度、压力和流量等10个相关变量，建立Isomap-MPA-LSSVM 软测量模型对VCM 转化率进行预测。根据收集的历史数据，选取具有代表性的5釜共1 500组数据，对该数据进行Isomap降维处理，将降维后数据中的1 200组作为训练集，后300组作为测试集，采用MPA 优化LSSVM 中参数，实现对转化率的预测。设定算法迭代次数为50，种群个数为20，LSSVM 中惩罚因子γ 与核参数σ 的寻优范围分别为[0.1，100]和[0.01，100]，迭代完成时，算法寻得的最优参数：γ=51.75，σ=0.015，賦值给LSSVM 进行预测。

为了验证所提软测量模型的有效性，引入了另外2 种模型进行比较，分别为MPA-LSSVM 和LSSVM 模型。图6—图8依次是LSSVM，MPALSSVM和Isomap-MPA-LSSVM 模型对VCM 转化率的预测结果，图9为3种模型的VCM 转化率预测误差对比。

从图6—图8中能看出Isomap-MPA-LSSVM模型的预测结果整体更趋近于真实值，通过图9中3种模型预测误差对比，LSSVM 和MPA-LSSVM模型预测的误差普遍在[-10，10]和[-6，6]，而Isomap-MPA-LSSVM 模型预测的误差普遍在[-4，4]，说明该模型预测误差线段整体最靠近于0，预测误差最小，精度最高。

表2为3种模型的性能比较结果，从表中可得，Isomap-MPA-LSSVM 模型比MPA-LSSVM 模型预测的MAE 降低了43.03%，RMSE 降低了30.27%，R2 值高了0.41%，比LSSVM 模型预测的MAE 降低了59.92%，RMSE 降低了52.24%，R2 值高了1.5%。因此，Isomap-MPA-LSSVM 模型的拟合度较好，预测精度较高以及稳定性能较强，能更加准确地预测VCM 转化率。

4 结语

本文鉴于PVC聚合过程中的VCM 转化率难以获取，通过收集相关的辅助变量建立软测量模型方法，从而实现了VCM 转化率精确预测，仿真实验结果验证了建立Isomap-MPA-LSSVM 软测量模型的可行性。

本文将Isomap，MPA 和LSSVM 三者结合，提出了一种基于Isomap-MPA-LSSVM 的软测量模型来预测VCM 转化率。首先对收集的数据进行Isomap降维处理，有利于对高维特征内在关系的挖掘以及数据有效信息的提取，消除数据的共线性和降低模型复杂度，再通过MPA 优化LSSVM 参数，构造软测量模型，仿真结果表明，所提模型能够精准预测VCM 转化率，满足了工业生产中的指标要求，对提高PVC 树脂的产品质量和产能有重要意义。然而，用Isomap算法对原始样本数据进行预处理，可能会丢失一些样本重要信息，将来有待进一步研究。