基于改进粒子群的分布式通信干扰资源分配

赵经纬　张君毅　李佳

关键词：人工智能技术;粒子群算法;改进粒子群算法;分布式通信干扰;资源分配

中图分类号：TN975 文献标识码：A DOI： 10.7535/hbgykj.2023yx01007

当今各军事强国都在追求复杂电磁环境下的信息优势，通信对抗对敌方通信链路进行干扰阻断，破坏敌方的指挥控制和信息传送，是获取战场信息优势的重要手段。随着“电磁频谱战”等作战概念的不断深入，体系化作战已成为必然趋势，如何高效运行己方作战力量、实现“多目标-多装备”高效资源分配，是未来分布式通信对抗作战指挥决策的核心关键。

传 统通信干扰资源分配主要依靠人工经验对多部干扰机/干扰力量进行分配调度，主观性较强，在针对单个目标时尚能达到较好的干扰效果/效益，但是在“多目标-多装备”场景下，不同指挥人员的经验对干扰效果存在很大的影响，干扰效益难以得到有效保障。因此，干扰资源分配调度对干扰效益和整体作战效能起着决定性作用。

干扰资源分配实际上是一类非线性整数组合优化问题，是一类NP难问题。针对此类问题，传统的优化算法主要包括0-1 规划、动态规划、博弈论等[1-4]，这些算法已无法满足当前需要。目前常用的进化算法包括遗传算法、蚁群算法、粒子群算法等等。文献[5—12]主要针对雷达网干扰资源分配场景进行建模和分配，证明了进化计算算法在资源分配问题中的有效性。文献[5—7]通过对遗传算法的编码方式进行改进或者与其他算法进行融合，改善了算法的局部搜索能力。文献[8—9]对蚁群算法在路径选择和信息素更新方面提出了改进，应用于资源分配问题中，提升了算法搜索速度和寻优能力。文献[10]将粒子群算法引入干扰资源分配问题中，验证了算法在资源分配问题中应用的可行性。文献[11—12]对粒子在解空间中的多样性和均匀性进行优化，避免算法陷入局部最优，提高迭代效率。通信干扰资源调度模型与雷达干扰资源调度模型本质上都要求干扰效益最大化，但二者建模的背景条件、目标函数和约束有所不同。在通信干扰方面，文献[13]针对通信对抗目标分配问题，在瞄准式干扰的背景下应用分布式拍卖算法，并对算法竞拍序列的产生使用轮盘赌策略进行优化，干扰效益更高，但是存在局部搜索能力较弱、易于陷入局部最优的问题。

本文针对分布式通信干扰资源高效分配需求，首先构建分布式通信干扰场景及资源分配数学模型;然后，为了对模型求解，针对粒子群算法收敛速度慢、易陷入局部极值的特点，提出一种改进的粒子群算法（improved particle swarm optimization，IPSO），实现干扰效益优化;最后，从干扰效益、迭代速度、收敛误差等角度出发，验证了本文所提算法的收敛性能。IPSO 算法采用自适应惯性因子和学习因子，引入遗传算法的变异策略，并实施精英保留策略，提升了干扰平均效益以及寻优概率。

1 分布式通信干扰场景及资源分配模型

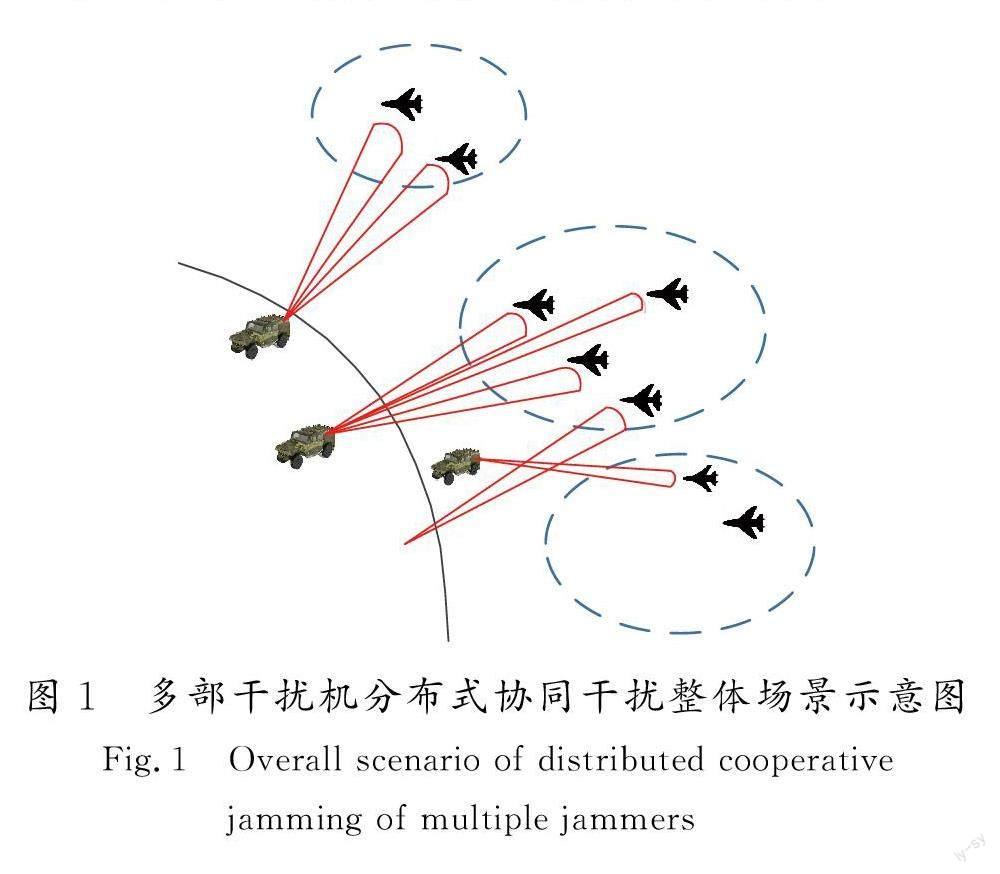
首先构建分布式通信干扰场景如下：假设我方M 部干扰机位置固定，均采取瞄准式干扰，且每部干扰机最多能够发射L 条干扰波束，以目标方向为法线方向发射干扰波束对其进行干扰。同时，所有干扰机的干扰波束功率P_j均可自主调节，且所有波束功率之和不得超过P_max。假设作战场景中有N 架飞机携带超短波通信电台组成若干定频通信网， 各通信目标的威胁程度W =[_w1，_w2，…，_wN]^T、通信功率P_t 已通过前期侦察及情报综合分析获取，利用多部干扰机对多个通信目标进行分布式协同干扰的场景如图1所示。

相比于基本粒子群算法，本文改进的粒子群算法在后期种群平均Hamming距离更低，说明算法向gbest收敛的性能更好。

3.3 算法性能对比

3.3.1 干扰效益对比

为验证所提算法的性能，选择按照3.1节参数进行迭代，得到本文改进粒子群算法（IPSO）、文献[5]的改进小生境遗传算法、基本粒子群算法（PSO）和基本遗传算法（GA）的单次运行收敛曲线，如图3所示。

首先进行单次收敛对比。由图3可看出，算法单次收敛曲线具有阶梯型的特征，这说明干扰资源分配问题的目标函数是一种多峰的非线性函数，也说明算法在进行全局寻优。本文改进粒子群算法通过15代收敛至全局最优值6.835 7，文献[5]算法在第217代收敛至全局最优值6.835 7。而粒子群算法和遗传算法分别在78代和102代收敛至局部最优值6.829 4和6.806 0。由此可见，改进的粒子群算法在收敛速度以及避免陷入局部极值的性能上均更优。

进行多次实验验证本文算法的性能优势。在上述场景和参数设置的条件下，分别使用IPSO、文献[5]的改进小生境遗传算法、PSO 和GA 进行100次迭代后取平均，得到的结果和平均收敛曲线分别如表2和图4所示。

如表2和图4可见，改进的粒子群算法在干扰效益高于文献[5]算法、PSO 和GA 的同时，所需的收敛代数和收敛时间均更低。这说明本文算法具有更好的搜索能力，提高了收敛性。

将干扰机数量M 、干扰波束数量L、目标飞机数量N 进行更改，重新进行实验。为了测试算法在不同场景的适应性，采取随机生成数据的方式进行验证，在保证对于同一规模下的不同算法，输入的通信功率、天线增益、距离等参数均相同的条件下，进行100次蒙特卡洛实验。计算平均干扰效益（目标函数值），得到的结果如表3所示。

从以上数据可以看出，改进粒子群算法相较于文献[5]算法、PSO 和GA 在不同干扰机数量、干扰波束数量、目标数量的情况下，均能获得较高的干扰效益，对干扰资源进行更加合理的分配。这说明算法相对于文献[5]算法、PSO 和GA 搜索能力更强，跳出局部极值的能力更强。

3.3.2 收敛误差对比

对比算法的收敛误差。本文定义算法的收敛误差由式（10）计算：

error=E_best-E， （10）

式中：error为收敛误差;E_best为全局最优目标函数值;E 为一次实验所获得的干扰效益值。

根据式（10）及表3中场景进行蒙特卡洛实验所获得的每一次实验的干扰效益值与全局最优值作差，计算算法的收敛误差，所得结果如图5和表4所示。

如图5所示，经过100次实验，本文算法在各种场景下的收敛误差均明显低于文献[5]算法、PSO和GA，更加接近全局最優。

在图5和表4中场景①到场景⑥的条件下，在场景规模增大的情况下，由图5可见，本文算法在这些场景下的收敛误差和平均收敛误差均低于文献[5]算法、PSO和GA。由此可见，本文算法的收敛性能优于文献[5]算法、PSO和GA，具有较好的统计性能。

4 结语

针对分布式通信干扰场景下面临的资源分配效率低、干扰效益无保障等问题，首先设计了分布通信干扰场景的数学模型;其次为了改进粒子群算法易“早熟”收敛的特点，采用将自适应惯性因子和学习因子引入遗传算法中的变异策略，并采取精英保留策略，对粒子群算法进行了改进。仿真实验表明，改进的粒子群算法相较于小生境遗传算法、粒子群算法和遗传算法，搜索能力更强，在场景规模增大的情况下，能够获得更高的干扰效益，并且所需的收敛时间更短、收敛误差更小。

因此，本文改进的粒子群算法能够实现对干扰资源的合理调度与分配。下一步将在数学建模中考虑更多的因素，并进一步提升粒子群的收敛速度，以适应更广泛的场景，实现对干扰资源更合理的分配。