图解:让数学解题思维可视
2023-08-11周炎


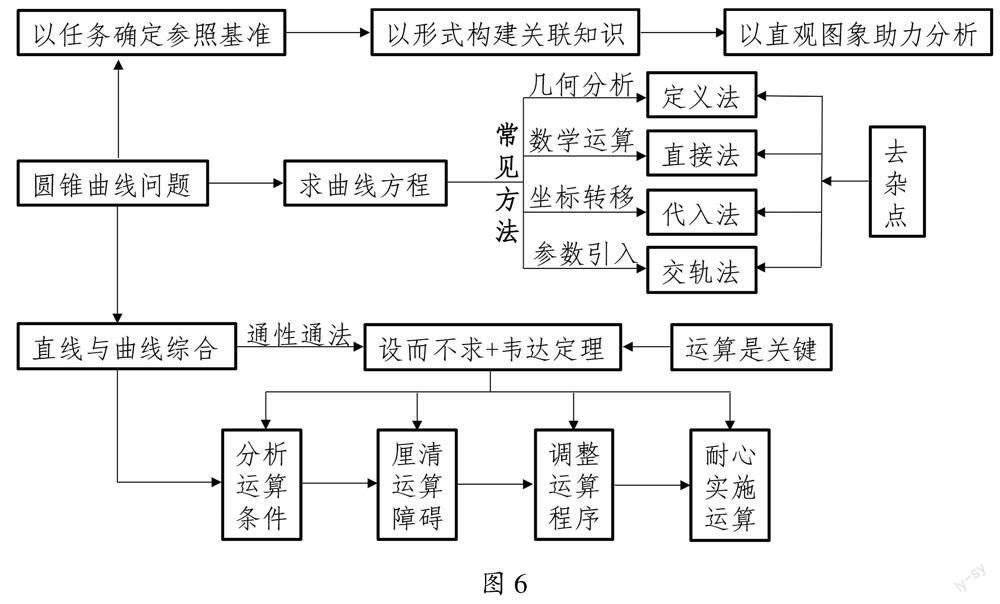
【摘 要】 对2022年新高考Ⅰ卷部分试题的解题思路进行研究,借助图示逐步呈现解题思路,让思维可视.既使得教师的解题教学看得见、摸得着,又为学生后续解题提供良好的解题范式,促进师生解题能力的共同提高.
【关键词】 高考试题;图解;思维可视
1 引言
在日常教学中,经常听到老师们抱怨:“这样的题型讲过好几遍了,学生遇到还是不会做,该怎样讲,他们才能掌握解题思路、找到最为合理的解题路径呢?”其实,不仅仅老师抱怨,学生听完一节数学课后也在想:“老师今天讲了几个例题,听是听懂了,但下次遇到新的题目,我怎么做,才能像老师那样找到解题思路呢?”究其原因,我们的高中教师经过多年的解题磨炼,对绝大部分题目的解决思路了然于胸,在给学生讲解时有些想当然,未能有效地将审题、析题的路径清晰地呈现给学生;而学生则是第一次遇到这样的题型,或者说也没遇到几次,对学生来说是全新的内容,要想很快掌握,确实有些勉为其难.
美国数学家波利亚在其专著《数学的发现》中强调:中学数学的主要任务就是加强解题训练[1].但加强解题训练并不意味着搞题海战术,对此,罗增儒教授提出:“分析典型例题的解题过程是学会解题的有效途径.”[2]那么,分析典型例题的解题过程的有效途径又是什么呢?笔者认为可以用流程图、树形图等可视化工具,将教师的思维路径呈现给学生,使学生看得见、摸得着,潜移默化中成为学生分析问题的方法.本文尝试借助图形对2022年新高考全国Ⅰ卷部分试题进行剖析,以期抛砖引玉.
2 典例呈现 2.1 按图索“迹”审核心
典例1 (2022年全国新高考Ⅰ卷第18题)记△ABC的内角A,B,C的对边分别为a,b,c,已知 cosA 1+sinA = sin2B 1+cos2B .
(1)若C= 2π 3 ,求B;
(2)求 a2+b2 c2 的最小值.
关键点击 解决本题的关键:(1)明晰已知条件的化简方向,能熟练运用倍角公式及两角和差公式化简;(2)理解本题中角的关系是已知条件,能把第二小问中关于边的式子用正弦定理转化为关于角的式子,构造关于角的正弦或余弦的目标函数再研究最值.
图示解读 首先审明已知条件与目标的差别,明晰条件与结论转化的方向,以建立两者之间的联系.对于第(1)小问,目标是求单角B,故很明显应将倍角转化为单角,再将代数式化为整式,观察等式特征知可运用两角和差公式化得cos(A+B),由角C已知,進而求得角B;对于第(2)小问,从问题出发,研究的是边有关的最值,联系已知条件,明晰应将边化为角,此时还含有三个角,故借助第(1)问的化简结果探寻三个角之间的关系以达到消元的目地,最终转化为仅含一个未知量的目标函数最值问题. 感悟 三角函数解答题是历年高考必考题型,一般位于解答题的前两题位置,其难度适中,正常来说是属于大部分学生都能得高分的题型.但从学生答题情况统计结果来看,对于第二个问题作答情况很不理想,学生普遍反映解题时目标不够明确,未能有效转化求解.数学解题时首先要培养学生的目标意识,对此可借助流程图来帮助学生联系已知条件与所求目标,根据流程图逐步剖析题中信息,领会命题人的意图,找到解题路径,进而不断提升学生数学审题能力. 典例2 (2022年全国新高考Ⅰ卷第22题)已知函数f(x)=ex-ax和g(x)=ax-lnx有相同的最小值.(1)求a;(2)证明:存在y=b直线,其与两条曲线y=f(x)和y=g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.
关键点击 解决本题第(2)问的关键:(1)善于将研究目标细化分解,逐个突破;(2)能熟练运用导数研究中常见的切线放缩、构造同构函数等技巧.
图示解读 首先对要研究的目标进行分解,细分为3个小目标,从而使得问题的研究更具体,易操作;其次对3个小目标的研究可通过构造函数,转化为研究三个函数的零点问题来实现,其中涉及分类讨论,进而明确了确实存在b,有x2=x3;再次结合指对代数式的结构特点,构造同构函数研究出单调性,明确x1与x2、x2与x4的关系;最后根据b建立x1,x2,x4的联系,实现问题的证明. 感悟 导数综合问题一直以来作为高考的压轴大题出现,是有效区分学生能力高低的关键题型.本题题干看似简洁明了,但很多考生读题之后,感觉无从下手直接产生了放弃的想法,仅有少数优秀的学生能继续下去.其实,一个数学问题往往是多个小问题的综合,我们可以采取如上树形图的方式引导学生将综合问题分解为若干个小问题,逐个击破.这样的解题训练,有利于学生在考试中得到更多的分数,有利于学生增强解题自信心;这样的图析方法,既为学生后续解题提供了借鉴的模板,又有助于学生分析、判断问题能力的提高.
2.2 借图把脉明路径 典例3 (2022年全国新高考Ⅰ卷第7题)设a=0.1e0.1,b= 1 9 ,c=-ln0.9,则( ).
A.a 关键点击 解决本题的关键:(1)构建a,b,c之间的联系;(2)熟悉导数问题研究中常见的切线放缩、构造函数等方法. 图示解读 先比较a,b,将a=0.1e0.1变形,小数化为分数,鉴于b= 1 9 ,故构造出分数 1 9 ,利用指对数运算性质将a化为 1 9 e 1 10 +ln 9 10 ,则问题转化为研究 1 10 +ln 9 10 与0的大小,再将 1 10 +ln 9 10 化为1- 9 10 +ln 9 10 ,则可构造函数研究单调性或借助熟悉的切线放缩不等式lnx 感悟 比较大小问题是全国高考常考题型,难度有增大的趋势,对考生的能力要求愈发提高.该题型虽短小精干,但内涵丰富,需要考生深刻挖掘两两或三者之间的潜在关联,既可以孤立的进行大小的比较,又可联系地深层分析继而整体研究确定大小关系.在试题讲解时,把两种路径清晰呈现,不仅能清晰地展示教师的思维历程,更能促使学生学会选择、推理、评价与监控. 典例4 (2022年全国新高考Ⅰ卷第21题)已知点A(2,1)在双曲线C: x2 a2 - y2 a2-1 =1(a>1)上,直线l交C于P,Q两点,直线AP,AQ的斜率之和为0. (1)求l的斜率; (2)若tan∠PAQ=2 2 ,求△PAQ的面积. 关键点击 解决本题的关键:(1)借助直线AP,AQ的斜率之和为0合理构建关联知识;(2)借助图形对tan∠PAQ=2 2 进行直观分析,实施转化;(3)对运算过程的整体把控. 图示解读 对于路径①,首先对目标分析知直线的斜率可用P,Q两点坐标来表示,故设出直线AP斜率为k,写出其点斜式方程,与双曲线方程联立,解出点P坐标.由直线AP,AQ的斜率之和为0,知仅需将P点坐标中的k替换为-k即得Q点坐标,据此实现直线l的斜率的求解.在此基础上结合∠PAQ对图形直观分析,发现直线AP的倾斜角为 π 2 - ∠PAQ 2 ,更进一步求出AP的斜率,代入第一问P,Q坐标中,从而求出AP,AQ长及∠PAQ的正弦达成面积的求解.对于路径②,由条件直线AP,AQ的斜率之和为0出发,用坐标表示,显露出两根之和、积的特征,故设出直线l的斜截式方程,运用设而不求、整体代入的思想构造出关于k,m的表达式f(k,m)=0,确定k的值.第二问的做法同路径①. 感悟 本题在第一问就涉及较为复杂的运算,一改以往的风格,虽是常规题型,却使得考生极不适应.考生在解题时又缺乏对运算路径的有效研判,导致运算过程繁琐,障碍重重,同时鉴于考试时间有限,只能被迫放弃.解析几何问题的求解实际上是一个不断优化运算路径的过程,在平时教学中应引导学生画出思维导图,深入分析运算条件,厘清运算路径,明析运算障碍,根据算理实施化简.学生明析每个路径的运算量、熟悉程度等,最终选择自己认为最有把握、最高效的路径.不必担心这样的分析会影响解题时间、进程,当学生习惯了这种方式,其数学理解能力和思维能力会得到很大提升,正所谓“磨刀不误砍柴功”;当学生习惯了这种方式,必然会“内化于心,外化于行”,从而形成属于自己的一套科学、严谨的解题模式. 2.3 以图升格拓思维一道数学试題的完整求解不能仅以思维的剖析、答题过程的呈现为最终目的,还应通过该题的求解领悟其背后所蕴含的数学思想方法、思维方式,从而做到举一反三、触类旁通,以兑现典型例题的教学价值.因此,还可借“图”对解题中所用的数学方法、思想进行梳理、提炼. 譬如对于典例2的提炼,如下图: 对于典例4的提炼如下图: 感悟 艾宾浩斯遗忘曲线揭示,信息输入大脑遗忘就随之开始,特别是在刚刚识记的短时间里遗忘最快.在此借助框图来提炼,可充分发挥其独特的“图像记忆”功能,促成学生记住、记牢知识与方法,并逐步建立与完善知识体系,夯实对知识的理解,擢升对方法的运用. 3 总结 解题就像开车,去一个陌生的地方,从起点到终点,人们常常借助导航系统.导航系统往往会提供几条路径供选择,有的路径会显示某段道路较堵,有的路径会显示红绿灯较多,有的路径会显示路程较远等.当选择某条路径行驶到中途,遇到前方拥堵或事故,导航会提示,并给出备选路径供选择.因此,解题时我们亦可借助思维导图,对解题路径“模拟导航”,将每条路径中存在的困难及困难的处理方法清晰呈现.以其直观性,使得学生对题的分析有直觉认识;以其思维性,使得学生明晰解题的思维过程;以其可读性,使得学生明确解题路径方向;以其实用性,丰富解题教学功能;以其指导性,提升学生解题能力. 参考文献 [1] [美]G·波利亚.数学的发现[M].刘景麟,曹之江,邹清莲,译. 北京:科学出版社. [2] 罗增儒.数学解题学引论(第二版)[M].陕西: 陕西师范大学出版社,2001:1. 作者简介 周炎(1980—),男,江苏南通人,中学高级教师;江苏省南通市高中数学学科带头人,江苏省南通市优秀教育工作者,曾获江苏省高中数学优秀课评比一等奖;主要从事高中数学教学研究;发表论文15篇.
