高中数学深度备课的层级架构

王永生 张文燕 黄语

【摘 要】  “深度备课”是学校教学变革的应然要求.以人教A版《数学选择性必修（第一册）》“圆与方程”为例，从“基于课程标准的单元设计、立足教材的课时设计和指向学生的活动设计”三个方面形成了高中数学“深度备课”的层级架构.

【关键词】  高中数学;深度备课;层级架构中国教育的素养时代已经来临.如何通过学校育人方式的变革培养学生的核心素养？这是当下各级各类学校都需要做出回答的核心问题.课堂改变学校才能改变，而改变课堂的前提是备好课.高中数学深度备课是指在厘清备课的层级关系（单元、课时和活动）的前提下，深度研读普通高中数学课程标准、教材、高考真题，并结合学情分析和教学资源，设计基于课程标准、能精准实现学生数学学科核心素养培养的学期课程纲要和单元（课时）教学方案的过程.因此，笔者认为，素养时代备课也应与时俱进，逐步走向专业化，即开展深度备课.有研究表明，开展深度备课需要架构好以下三个层级：基于课程标准的单元设计，立足教材的课时设计和指向学生的活动设计［1］.下面以人教A版普通高中教科书《数学选择性必修（第一册）》中“圆与方程”单元的备课为例，谈谈三个层级的具体做法.

1   基于课程标准的单元设计

长期以来，一线教师备课都很少考虑单元，更不关注课程标准.可素养时代，有学者认为在“核心素养—课程标准—单元设计—学习评价”这一环环相扣的教师教育活动的基本链环中，单元设计处于关键的地位，是撬动课堂转型的重要支点［2］.

随着新一轮课程改革的推进，素养时代单元设计将成为一线教师备课的新常态.那如何开展单元设计呢？这方面的研究较多.国外较为著名的是格兰特·威金斯和杰伊·麦克泰提出的“理解为先（UbD）模式”［3］，其基本思想是“逆向设计三阶段：明确预期学习结果、确定可接受的证据和规划相应的教学过程” ［3］.以此为基础，国内相继提出“基于课程标准的教学设计”［4］和“深度学习的实践模型”［5］等.《普通高中数学课程标准（2017年版2020年修订）》也给出了“主题教学设计”［6］的案例.这些设计的相同点是都含有“目标、过程和评价”三个关键词.基于此，笔者认为，深度备课的第一层级应是进行基于课程标准的单元设计，这里的单元特指课程标准中科学内容的二级主题，是以系统化的学科为基础所构成的“教材单元”（学科单元），设计时一般可遵循以下路径.

1．1 梳理课程标准，确定单元学习目标

单元学习目标是指完成对所选择单元的学习后，学生最终要达成的总目标.进行单元设计的首要任务是要明确将学生带到哪里，即先确定单元学习目标.

课程标准是规定某一学科的课程性质、课程目标、内容目标、实施建议的教学指导性文件，提出了面向全体学生的学习基本要求，反映了国家对学生学习结果的期望.因此，单元设计的起点应是梳理本章内容在课程标准中的界定的表述，并据此确定单元学习目标.

案例1  “圆与方程”在课程标准中的相關表述（节选）［6］

“圆与方程”是人教A版普通高中数学教科书《选择性必修（第一册）》“平面解析几何”主题下的二级主题.课程标准相关表述如下，其中的“内容要求”即为本单元的教学目标.

内容与要求：①回顾确定圆的几何要素，在平面直角坐标系中，探索并掌握圆的标准方程与一般方程;

②能根据给定直线、圆的方程，判断直线与圆、圆与圆的位置关系;

③能用直线和圆的方程解决一些简单的数学问题与实际问题.

1．2 研析高考试题，编制单元测试试卷

课标时代，教学的起点应为课程标准，终点则是高考试题，而中间过程则是教学应该有的使命和任务.如何才能知道学生是否已经达到课程标准的要求了呢？这就需要编制立足单元学习目标的单元测试试卷.等完成教学任务后，通过测试即可清楚学生学习的效果.可见，这是本单元学习的终结性评价，同时又是学期学习的过程性评价.编制高质量的单元测试试卷，这是一件非常专业的事情.为此，应先从研析高考试题入手.

案例2  五年高考课标全国卷对“圆与方程”的考查要点分析（以文科数学为例）

通过对高考试题的研析，基本能看清课程标准的显性考查，据此可编制本单元的测试试卷.其一般程序是列出双向细目表、逐一命制试题、组合试卷、审查试卷.下面就前两个步骤举例说明.

案例3  “圆与方程”单元测试试卷的命制

将单元学习目标①解构，可以分解出若干子目标，其中最重要的一个是根据已知条件求圆的方程.下面以此为例具体说明试题的命制.

试题命制可从分析高考试题入手，结合教材例习题进行改编.下面以上表中第17题的命制过程为例进行具体说明. 高考试题  （2011年高考辽宁卷第13题）已知圆C经过A（5，1），B（1，3）两点，圆心在x轴上，则圆C的方程是      .

教材例习题

1.（人教A版高中数学选择性必修（第一册）P88习题2.4第4题）圆C的圆心在x轴上，并且过点A（－1，1）和B（1，3），求圆C的方程.2.（人教A版高中数学选择性必修（第一册）P84例3）已知圆心为C的圆经过点A（1，1）和B（2，－2），且圆心C在直线l：x－y+1=0上，求圆心为C的圆的标准方程.

3.（人教A版高中数学选择性必修（第一册）P88习题2.4第3题）已知圆C的圆心在直线l：x－2y－1=0上，并且经过原点和A（2，1），求圆C的标准方程.

4.（人教A版高中数学选择性必修（第一册）P102复习参考题2第6题（3））求圆心在直线3x+y－5=0上，并且经过原点和A（3，－1）的圆的方程.

不难看出，这几道题条件基本是圆心在一已知直线上，并且经过两已知点.不同点是已知直线特殊（如x轴），或点特殊（如原点）.此外有些题是求圆的方程，而有些题是求圆的标准方程.但基本上都是考查用待定系数法或几何法求圆的方程.

当然，这只是“根据条件求圆的方程”这一子目标的一类问题，但在教材中能有这样的份量（一个例题三个习题），可见其重要性.在单元测试卷中为较好地考查此类问题，可分三个层次进行命题（易中难）.

第一层次跟高考试题和教材例习题一致，条件中有一个特殊，求圆的标准方程.

测试试题1  （容易题）求经过点A（1，1）和坐标原点，并且圆心在直线2x+3y+1=0上的圆的标准方程.

第二层次三个条件中没有一个特殊，求圆的方程.

测试试题2  （中档题）求过点 A（1，－1），B（－1，1），且圆心在直线x+y－2=0上的圆的方程.

由于是单元测试试题，应该有一定的综合性，于是可充分考虑综合考查单元学习目标①②，这是高考考查的主要方向，为此仍然与教材相结合，然后仿照命制试题.

教材例习题  5. （人教A版高中数学选择性必修（第一册）P103复习参考题第16题）求圆心在直线y=－2x上，并且经过点A（2，－1），与直线x+y=1相切的圆的方程.

仿此，第三层次保留圆心在已知直线上，并且与另一已知直线相切，求圆的方程.

测试试题3  （稍难题）求圆心在直线y=－4x上且与直线l：x+y－1=0相切于点P（3，－2）的圆的方程.

根据学生的学情和单元测试试卷的整体需要，可选择相应的题进行测试.按照双向细目表逐一命制好试题（一般都按易中难命制三道题）后，便可组合相应的测试试卷，一般分AB卷，一份用于测试，另一份用于跟进补偿性训练.

1．3 遵循学习规律，制定单元学习方案

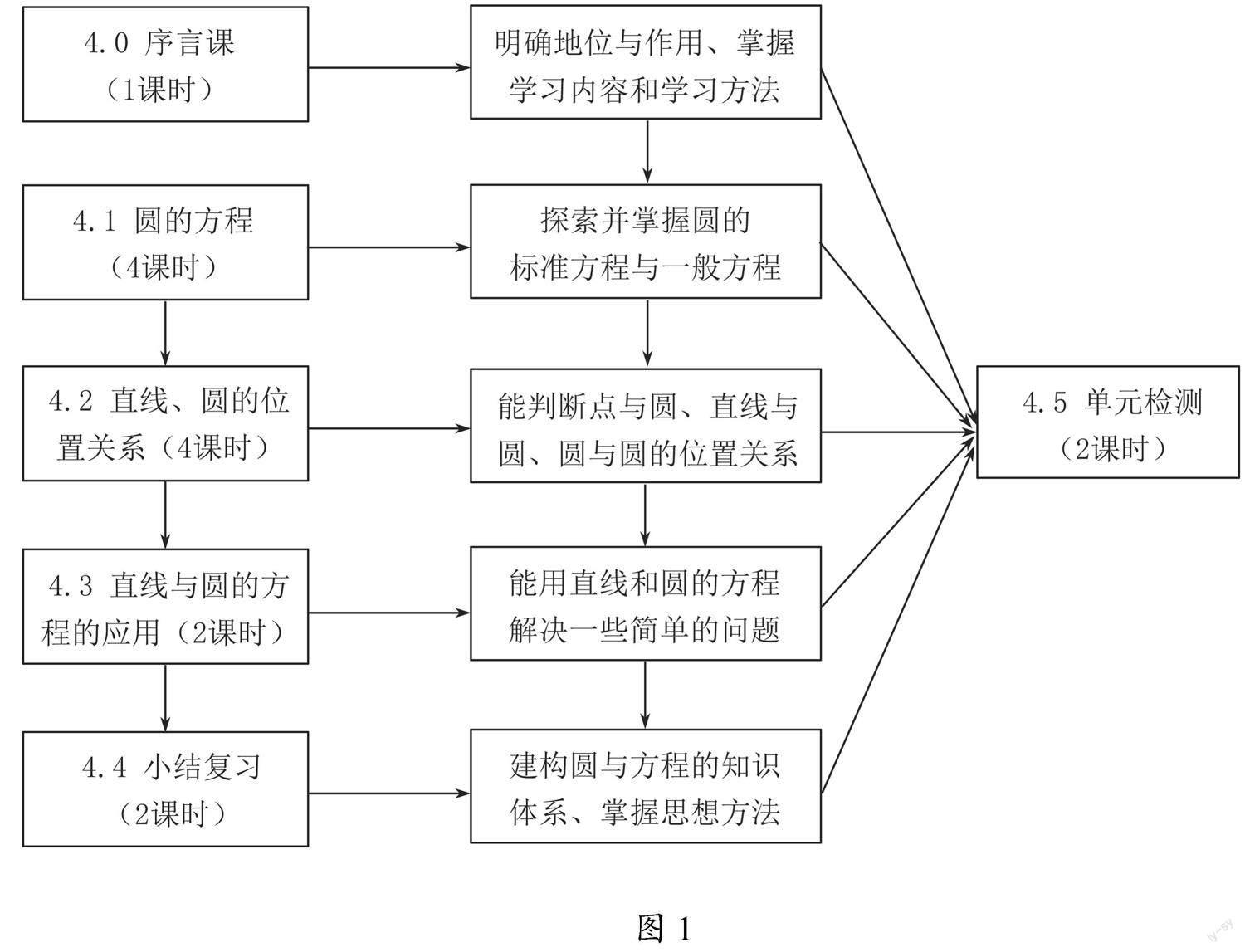
按照课程标准的要求，明确了学生通过本单元的学习后要达到的目标，结合学生学习的规律，可按照循序渐近的原则，制定单元整体的学习方案，其课时目标和相互之间的关系如图1所示.

单元整体课时计划的制定基于课程标准所确定的单元目标.遵循学习的规律，以目标为导向进行整体设计.其中4.1、4.2和4.3为完成单元目标的核心部分，需要10课时.而4.0、4.4和4.5为达成单元目标的辅助部分，在整个单元学习的过程中其重要性不言而喻.可事实是为了赶教学进度，这几个部分的落实质量相对较差.特别是序言课，一直以来都没有得到重视，有的教师也没有这个意识，而这恰恰是教学实施的一个盲区，必须引起足够的重视. 2   立足教材的课时设计 教材又称课本，它是依据课程标准编制的、系统反映学科内容的教学用书.课时设计必须立足教材，力争实现用教材教，为此，应做好“明确课时学习目标、形成课时学习测验和设计课时学习流程”三个方面的工作.

2．1 顺应教材编排，明确课时学习目标

使用教材，应先掌握教材的编排方式.教材的编排方式一般有四种，即直线式、螺旋式、分支平行式和綜合式.课时设计的起点应从整体把握教材入手，通过顺应教材编排，同时解构单元学习目标，最终明确课时学习目标.

案例4  “圆的标准方程（第一课时）”课时学习目标

“圆与方程”单元教材以螺旋式方式编排，其中圆的标准方程的概念最先安排，并贯穿单元始终.为此，理解、掌握并能灵活应用圆的标准方程的概念就显得十分重要.而此目标的最终达成却是螺旋式的，于是将单元学习目标①解构，其第一个子目标应是“理解、掌握并能灵活应用圆的标准方程的概念”.按照教材的编排，“圆的标准方程（第一课时）”的课时学习目标可确定为“形成圆的标准方程的概念；理解圆的标准方程的概念和简单应用圆的标准方程的概念”.

2．2 整合教材资源，形成课后学习测试

为能检查学生通过课堂学习后是否达成课时目标，需要优先制定评价标准，即课后学习测试，俗称课后作业.教材是课堂教学的第一资源，是课程标准的显性表现，一般都编排了足够的习题.人教A版普通高中数学新课程标准实验教科书（必修）配备了例题、练习、习题（AB组）和复习参考题（AB组）等供学习使用的测试题.这些例习题往往是高考命题的主要素材来源，为此，充分利用好这些测试题是课时设计必须重点考虑的问题.但是这些例习题却又是螺旋式编排的，于是，需要整体把握教材，将教材资源充分整合，有序列出课内训练和课后测试的试题.课后作业应与课时学习目标相匹配，最好要进行分层，按易中难设置.如教材所提供的资源不足，还得进行必要的补充. 案例5  “圆的标准方程（第一课时）”课后学习测试（节选）关于“圆的标准方程（第一课时）”的学习目标“形成圆的标准方程的概念”，其形成概念的过程即是“轨迹法”求曲线（圆）方程的方法，教材提供的习题已足够，可分层安排课时学习测验如下：

（A层）（人教A版高中数学选择性必修（第一册）P88习题2.4第7题）等腰三角形顶点A的坐标是（4，2），底边一个端点B的坐标是（3，5），求另一个端点C的轨迹方程，并说明它是什么图形？

（B层）（人教A版高中数学选择性必修（第一册）P88习题2.4第8题）长为2a的线段AB的两个端点A和B分别在x轴和y轴上滑动，求线段AB的中点的轨迹方程.

（C层）已知点M（x，y）与两个定点M1，M2距离的比是一个正数m，求点M的轨迹方程，并说明它是什么图形（考虑m=1和m≠1两种情形）.2．3 根据课型特点，设计课时学习流程

明确了课时学习目标，形成了目标指向的课后学习测试后，应根据课型的特点，学生的学习情况和教材的编排方式，设计出简约的课时学习流程.仍以“圆的标准方程（第一课时）”为例，前面对教材的编排方式已进行了分析.而这一课时的定位应是概念学习课，按照数学概念课的学习过程，必须经历“形成、理解和应用”三个阶段，考虑到“圆的标准方程” 这一概念在此单元中的重要性，可设计如图2的课时学习流程.

3   指向学生的活动设计

上一轮新课程改革要求转变学生的学习方式，倡导自主学习、合作学习和探究学习.应当说，经过十多年的实践，这一理念已深入人心.但把课堂还给学生，让学生由被动学习向能动学习转变，真正实现课堂的转型，新一轮课程改革还有好长一段路要走.但无论如何，要让学生变被动为能动，必须进行指向学生的活动设计，在课时目标的指引下，立足学生的实际，创造性地进行学习任务的设计，让学生在任务的驱动下，通过自主、合作和探究，最终达成课时学习目标.

3．1 结合学生特点，设定活动学习目标

长期以来，课堂一直由教师所控制，还课堂给学生的关键是让学生在课堂上能够“动”起来.这样的“动”却不能是随意的，而应当是指向一定目标的学习活动.可事实是，很多课堂学生要么乱动，要么不允许动.组织有意义的学习活动需要课前进行系统而又精心的设计.为此，需要充分结合学生的特点，围绕课时學习目标，通过分解，依次设定相应的活动学习目标.

3．2 立足学习过程，制定活动学习评价

为使学习始终不偏离轨道，并随时清楚活动的效果.这就需要立足整个学习过程，事先制定相应的活动学习评价.这样的评价能促进学生对学习活动进行反思和自我监控，一般是整个课时的形成性评价，但又是该活动的终结性评价.其目的是检测学习活动是否达成活动学习目标，以便及时进行教学改进，从而确保整个课时目标的有效达成.

3．3 合理创设情境，设计深度学习活动

学习活动不能是为了活动而活动，而应使学生充分参与其中，在增加学习体验的过程中能促进学生对学习内容的深层次理解.但课堂学习的时间和空间毕竟有限，因此可以充分利用多媒体技术，合理创设学习活动的情境，使学生在情境中实现深度学习，这才是最有意义的学习活动设计.

下面结合前面的分析，就一个课时目标的达成进行相应学习活动的设计说明.

案例6  “圆的标准方程（第一课时）”学习活动设计（节选）

目标1：形成圆的标准方程的概念（课时目标）

活动1：（活动目标）圆的知识准备

情境创设：（1）视频播放：中秋赏月；

（2）多媒体演示：若动点到定点距离为定长，描绘出动点的运动轨迹.

思考1：动点的运动轨迹是什么图形？

任务1：请给圆下一个定义（描述性），并指出其要素.

活动2： （活动目标）形成圆的标准方程（已知轨迹求方程）

思考2：在平面直角坐标系中，如何确定一个圆呢？

任务2：如图3，在平面直角坐标系中，圆C的圆心坐标为C（a，b），半径为r，如何写出圆的方程？

思考3：圆心在坐标原点，半径长为r的圆的方程是什么？

思考4：用轨迹法（直接法）求曲线的轨迹方程的步骤有哪些？

活动3： （活动目标）求圆的标准方程（未知轨迹求方程）

思考5：已知点P（2，0），Q（8，0），点M与点P的距离是它与点Q的距离的 1 5 ，求点M的轨迹是什么图形？

任务3：用《几何画板》探究点M的轨迹，并给出轨迹的方程.

检测：（人教A版高中数学选择性必修（第一册）P89习题2.4第3题）已知点M与两个定点O（0，0），A（3，0）的距离的比为 1 2 ，求点M的轨迹方程.

每一节课的教学都需要达成一个或几个课时目标，而为了达成每一个课时目标，都需要进行一系列的学习活动的设计. 这些活动的设计需要指向学生，并依次达成各自的活动目标.活动设计指向学生，就是以学生的学习为中心，立足整个学习过程，为学生创造学习体验的机会，并促进学生进行深度学习，同时引导学生进行自我反思和调控，最终在达成学习目标的过程中使学生学会学习.在素养时代，为使备课走向专业化，我们倡导实施深度备课，即从整体到局部，依次完成“单元、课时和活动”的三级设计.其中，单元设计应以课程标准为纲；课时设计应以教材为基；而活动设计则须以学生为本［1］.建立这样的层级架构，只是为了提供一种备课的专业模式.同时，对于学科的差异性，可作适当的变通.但是在具体实践时，还应有所侧重.建议日常的集体备课应突出单元设计，而教师独立备课时，则应加强对教材文本的研读，并在指向学生的活动设计中可适当彰显教师的个性和教学智慧.

参考文献

［1］  骆波.初中物理深度备课的层级架构［J］.基础教育课程，2017（01）：58-64.

［2］  钟启泉.基于核心素养的课程发展：挑战与课题［J］.全球教育展望，2016（01）：3-25.

［3］   ［美］格兰特·威金斯， 杰伊·麦克泰.理解为先模式：单元教学设计指南（一）［Ｍ］.盛群力，沈祖芸，柳丰， 等，译． 福州：福建教育出版社，2018.1．

［4］  李锋.基于标准的教学设计：理论、实践与案例［M］.上海：华东师范大学出版社，2013.8.

［5］  刘月霞，郭华.深度学习：走向核心素养［M］. 北京：科学教育出版社，2018.11.

［6］  中华人民共和国教育部.普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2018.1.

作者简介

王永生（1974—），男，云南大理人，数学教育硕士，中学正高级教师，云南师范大学硕士研究生导师，大理大学硕士研究生导师；荣获云南省“万人计划” 之“教学名师”、大理州首届“白州教学名师 ”、大理市“名教 师”、优秀教师、先进教育工作者、优秀共产党员、大理市“名师讲学团成员”等称号；云南省高中数学青年教师说课比赛一等奖获得者；主要从事课程和教学论、中学教育教学管理、教师专业化发展和中小学数学教育教学的研究工作；发表文章 １１０ 多篇．

张文燕（1984—），女，中学高级教师，高中数学教研组长;从事数学教育研究17年.

黄语（1997—），女，云南保山人，中学二级教师.