巧用多边形定则快速解决高考疑难问题
2023-08-10钟用庭
钟用庭
(海南省文昌中学)
高中物理的力学问题,是高考的一大热点和难点。关于力学问题的解法,一般常用平行四边形定则,而力的多边形定则却很少被用到。然而实际上多边形定则和上述方法相比,其优势在于更加简洁、高效、直观,也容易被学生快速掌握与应用,尤其适用于某些疑难选择题的快速解答,省去了繁杂的计算分析过程。现将此类高效解法举例介绍如下。
平行四边形定则
根据平行四边形定则,合力和两个分力必然构成一个封闭的矢量三角形,如图1所示。
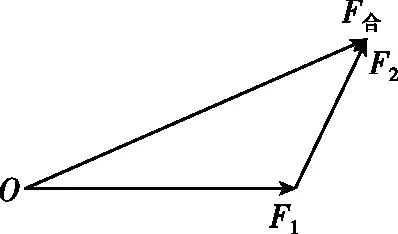
图1
多边形定则
由三角形定则可以推广到多个力的合成情况:由共点O顺次首尾相连作出各力的图示,然后由共点O向最后一个力的末端所引的图示即为要求的合力,如图2,3所示。
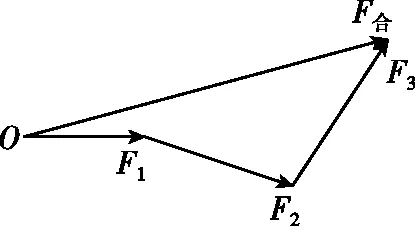
图2
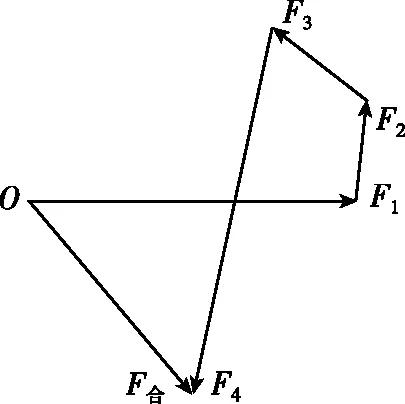
图3
下面将举例说明多边形定则法的优越性:
一、多边形定则的优越性之一——简洁直观
【例1】如图4,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦。已知楔形物体b静止时,a静止在b的斜面上。现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能 ( )
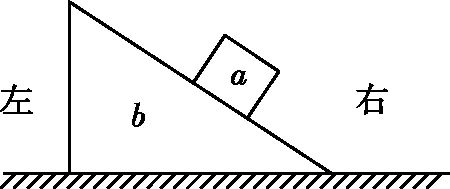
图4
A.a与b之间的压力减少,且a相对b向下滑动
B.a与b之间的压力增大,且a相对b向上滑动
C.a与b之间的压力增大,且a相对b静止不动
D.b与地面之间的压力不变,且a相对b向上滑动
【常规解法】a和b有一个共同的向左的初速度,且b与地面之间有摩擦,所以a和b所受的合外力水平向右,a所受的合外力同样水平向右。若a、b相对静止,当a受到的摩擦力方向沿斜面向上时,对a进行受力分析,如图5。
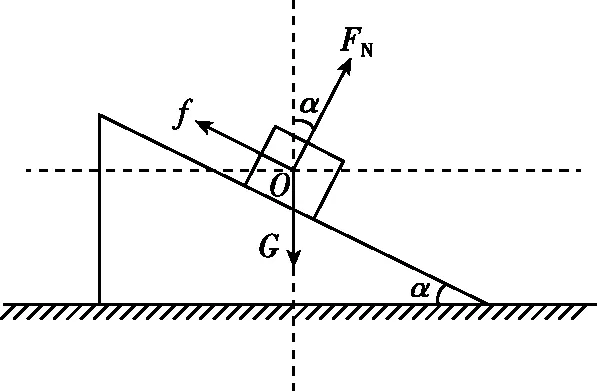
图5
a和b原来静止,a受重力、支持力、摩擦力三力平衡,根据平衡条件可知,竖直方向FNcosα+fsinα=G。当a和b相对静止,并且共同向左做减速运动,合外力为F,摩擦力f等于0时,如图6所示。此时竖直方向合外力为零;FN′ cosα=G,解得FN′ >FN,故a与b之间的压力增大,故A错误;当a受到的摩擦力方向沿斜面向下时,此时有两种情况:第一种情况,假设物块a、b恰好仍相对静止,f达到最大静摩擦力时,对a进行受力分析,如图7,竖直方向加速度为零,竖直方向G+fsinα=FN′ cosα,由牛顿第二定律得,水平方向有FN′ sinα+fcosα=F,F=ma,解得FN′ >FN。故a与b之间的压力增大,此时物体a、b相对静止,故C正确;第二种情况,当加速度a继续增大时,此时物块a相对于b就会发生向上滑动,故B正确;对整体研究,在竖直方向上,若两物体相对静止,竖直方向上没有加速度,则b与地面之间的压力等于两物体的重力之和,保持不变;若物块a相对向上滑动,则a具有竖直向上的分加速度,即对整体的牛顿第二定律可知,系统处于超重状态,b与地面之间的压力将大于两物体重力之和,故D错误,故选BC。
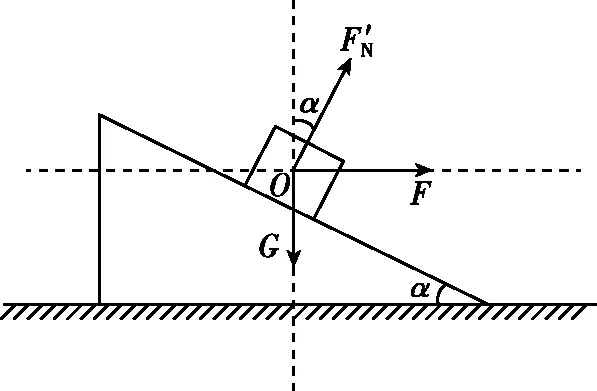
图6
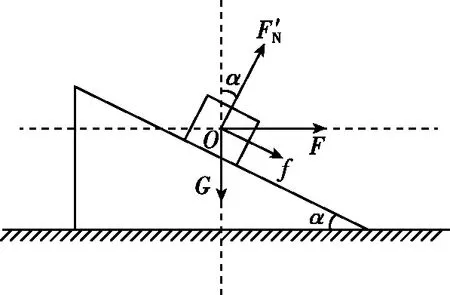
图7
【多边形定则解法】如图8所示,可以设F合1=ma1,F合2=ma2,F合3=ma3。随着加速度a的增大,物块a和b之间的作用力F不断增大,A错误;当a、b间的作用力由F0增大到F1时,摩擦力为0;再增大到F2时,摩擦力反向达到最大静摩擦力。当加速度a>a2时,比如a=a3,物块a沿着b的斜面向上滑动(只要物块a的加速度不在水平方向上就会发生相对滑动),所以BC正确;当物块a相对b向上滑动时,F3和fmax的合力的竖直分量F3y>mg,根据牛顿第三定律,b与地面之间的压力会增大,所以D错误。
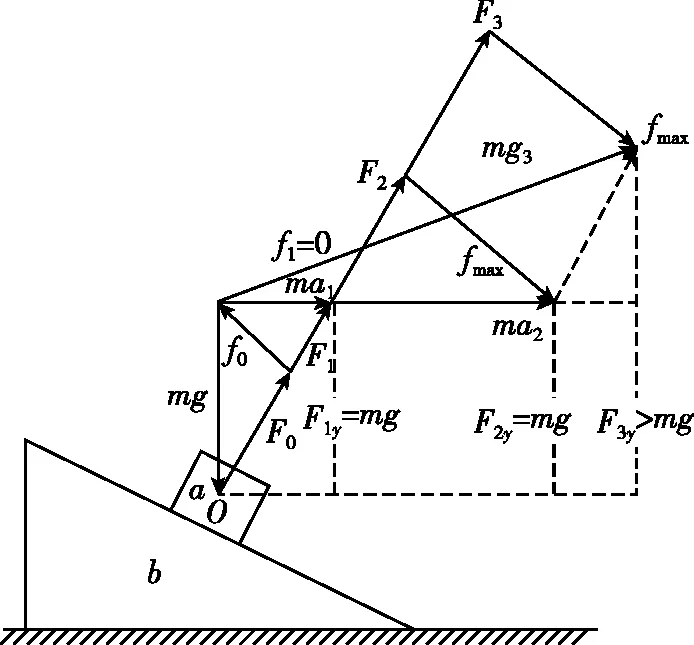
图8
【答案】BC
【点评】本题得分率很低,因为常规解法繁琐冗长,在短时间内极易出错或无从下手,并且很多杂志书刊很少采用此题,即使沿用此题,给出的解法也不十分完美,甚至是错误的。由此可见,在本题中多边形定则法简洁明了地得出了a、b之间的压力变化规律和a物体的运动状态关系,给解答此类问题提供了较为清晰、准确的解题思路。
二、多边形定则优点之二——发现瑕疵
【例2】如图9,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上。a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动。当它们刚运行至轨道的粗糙段时 ( )
A.绳的张力减小,b对a的正压力减小
B.绳的张力增加,斜面对b的支持力增加
C.绳的张力减小,地面对a的支持力增加
D.绳的张力增加,地面对a的支持力减小
【常规解法】在光滑段运动时,物块a及物块b均处于平衡状态,对a、b整体受力分析,受重力和支持力,二力平衡。对b受力分析。如图10所示,受重力mg、斜面的支持力FN、绳子的拉力F,根据共点力平衡条件,有
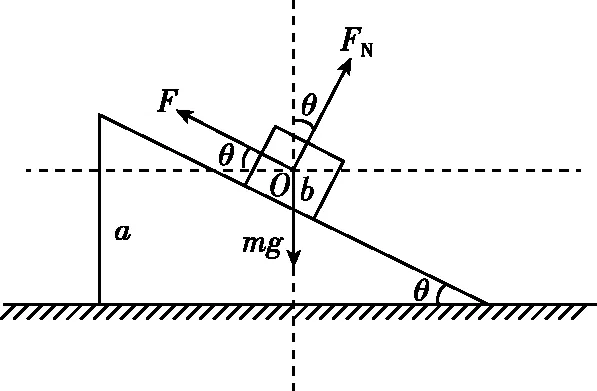
图10
Fcosθ-FNsinθ=0
①
Fsinθ+FNcosθ-mg=0
②
由①②两式解得F=mgsinθ,FN=mgcosθ,当它们刚运行至轨道的粗糙段时,减速滑行,系统有水平向右的加速度,此时有两种可能;
当物块a、b仍相对静止,竖直方向加速度为零,由牛顿第二定律得到
Fsinθ+FNcosθ-mg=0
③
FNsinθ-Fcosθ=ma
④
由③④两式解得F=mgsinθ-macosθ,FN=mgcosθ+masinθ,即绳的张力F将减小,而a对b的支持力变大;再对a、b整体受力分析竖直方向重力和支持力平衡,水平方向只受摩擦力,故地面对a支持力不变;若物块b相对于a向上加速滑动,绳的张力显然减小为零,物块b具有向上的分加速度,是超重,因此a对b的支持力增大,斜面体和滑块整体具有向上的加速度,也是超重,故地面对a的支持力也增大。综合上述讨论,结论为绳子拉力一定减小;地面对a的支持力可能增加;a对b的支持力一定增加,故ABD错误,故选C。
【多边形定则解法】如图11所示,当a、b物体向左减速运动时,加速度越大,a、b之间的作用力F越大,绳子拉力越小,直到绳子的拉力为0;加速度再增大,b物体相对a沿着斜面向上滑动,比如在作用力F3,合力为ma3时,b物体相对a向上滑动,当加速度由a1变为a2、a3时,绳子拉力一定减少,a对b的支持力一定增大,即ABD选项均是错误的。只有当b相对a向上滑动时,a与b之间的弹力的竖直分力才大于mg,比如F3的竖直分力大于mg,所以C选项只有在满足b物块相对于a沿着斜面向上滑动这个条件下才正确。
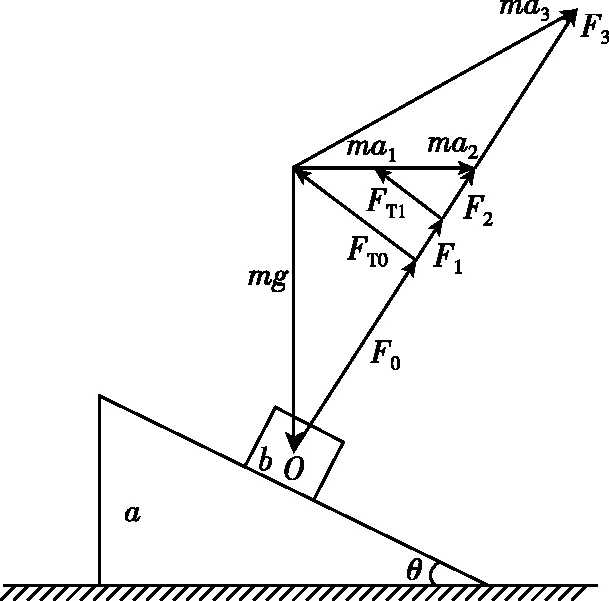
图11
【答案】C
【点评】此类问题具有较大的区分度,全国各地高考往往每隔几年就会出现这种题型。很多学生用常规解法经常出错,而多边形定则较好地解决了这一问题。只要掌握了多边形定则方法,可以大大提高学生的正确率。另外从这个多边形定则作图法当中,只有加速度大于a2,物体b才沿着斜面上滑,才有地面对a的支持力这一情况出现,因此从图中也能比较容易发现本题C选项的瑕疵。
三、多边形定则优越性之三——解答综合性难题
【例3】水平地面上放有三角形物块A,物块A的斜面光滑,用轻弹簧和挡板C将物块B连接在斜面上,如图12所示,A、B一起向右做加速运动。某时刻发现连接C、B的轻弹簧长度变短,则下列判断正确的是 ( )
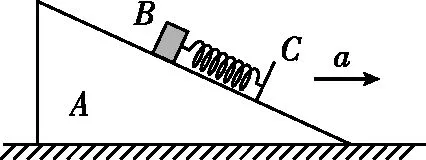
图12
A.物块A的加速度一定变大
B.轻弹簧对B一定存在沿斜面向上的弹力
C.物块B对斜面的压力一定变小
D.物块B对斜面的压力可能变大
【常规解法】系统的加速度向右,则合力向右。轻弹簧长度变短,则物体B受到向右的合力变小,故加速度变小,故A错误;若经弹簧原来和变短后仍处于伸长状态,则弹簧的弹力沿斜面向下,故B错误;物块B受重力mg、斜面支持力FN,和弹簧的弹力F,垂直斜面方向,FN-mgcosθ=masinθ(θ为斜面角),加速度变小,则FN变小,故C正确,D错误。故选C。
【多边形定则解法】如图13所示,当弹簧处于压缩状态,弹力为FT1,加速度为a1,合力为ma1;弹簧越短,FT1越大,F1越小,合力ma1越小(如图13所示,F1′ 、FT1′ 、ma1′ ),所以A选项错误;当加速度为a2的时候,弹簧的弹力FT2=0,所以B选项错误;当弹力为FT3时,弹簧处于伸长状态,弹簧越短,FT3越小,F3越小,合力ma3越小(如图13所示,F3′ 、FT3′ 、ma3′ ),所以根据弹簧处于压缩和伸长这两种情况,C选项正确,D选项错误。
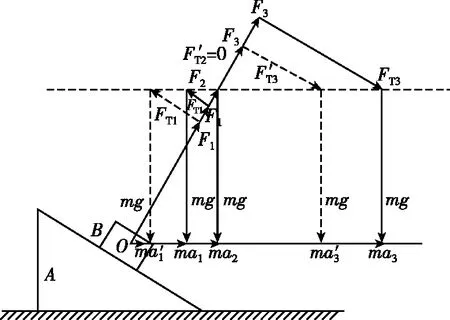
图13
【答案】C
【点评】在日常考试中,有关弹簧的题目与斜面结合难度很大,学生往往一头雾水。而多边形定则法能够帮助学生清晰地认识到弹簧什么时候伸长,什么时候缩短,对弹簧的状态有个直观的认识。通过运用多边形定则法可以简单明了的解决这类综合性难题,更易让学生理解物理定则的本质。
四、结束语

