“关联气体”问题解题“三步曲”
2023-08-10王栋然
王栋然
(宁夏回族自治区银川市第九中学)
多个理想气体相互联系所构成的系统称为“关联气体”系统,关联气体在高考热学大题中有着较高的考查频率。对于关联气体问题的解决,有着相对固定的三个思维步骤:
①分别对各部分理想气体列出理想气体状态方程;
②列出压强关联方程;
③列出几何关联方程。
下面通过几道高考真题来例析在关联气体问题中如何利用这“三步曲”有效解题。
一、“活塞类”关联气体问题
(一)单一活塞类关联气体问题
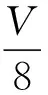
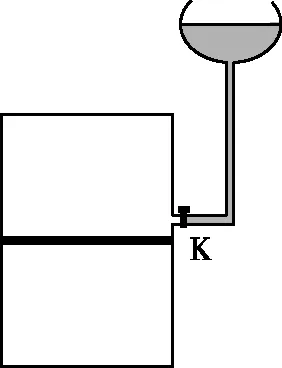
图1
【试题分析】本题通过活塞将上下两部分定质量气体关联起来形成“关联气体”。设活塞再次平衡后,活塞上方气体的体积为V1,压强为p1;下方气体的体积为V2,压强为p2。如图2所示。
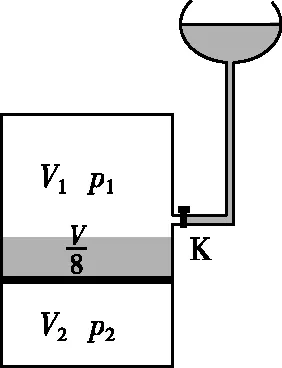
图2
第一步曲——分别对各部分理想气体列出理想气体状态方程
根据题中条件“导热材料”“外界温度保持不变”可知上下两部分气体都发生等温变化,根据玻意耳定律
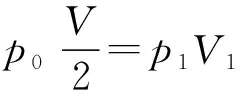
①
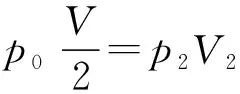
②
第二步曲——列出压强关联方程
设活塞上方液体的质量为m,活塞受力平衡
p2S=p1S+mg
③
第三步曲——列出几何关联方程
因为汽缸总容积保持不变,根据几何关系可得
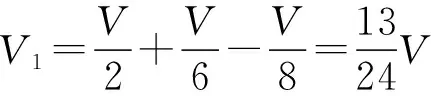
④
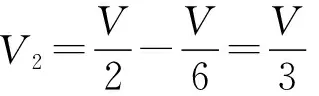
⑤
(二)双活塞类关联气体问题
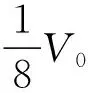
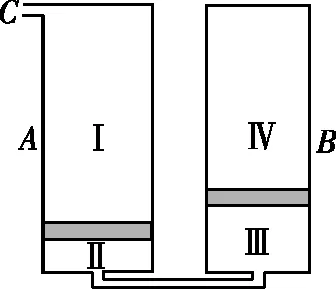
图3
将环境温度缓慢改变至2T0,然后用气泵从开口C向汽缸内缓慢注入气体,求A汽缸中的活塞到达汽缸底部后,B汽缸内第Ⅳ部分气体的压强。
【试题分析】两个活塞将气体分为Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,其中Ⅱ、Ⅲ气体作为定质量整体与定质量的Ⅳ气体构成“关联气体”。设当A中的活塞到达汽缸底部时Ⅱ、Ⅲ中气体的压强为p1,此时Ⅳ内的气体压强为p2。设此时Ⅱ、Ⅲ中气体体积为V1,Ⅳ中体积为V2。
第一步曲——分别对各部分理想气体列出理想气体状态方程
根据“缸壁导热”以及环境温度变化为2T0可知,缸内气体体积、压强、温度均变化。根据理想气体状态方程
①
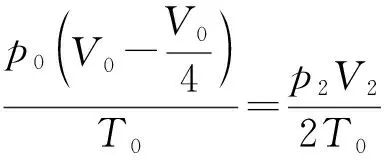
②
第二步曲——列出压强关联方程
右边轻质活塞受力平衡p1S=p2S
③
第三步曲——列出几何关联方程
Ⅱ、Ⅲ中气体最终全部压入右缸,根据体积关系V1+V2=V0
④
(三)连杆活塞类关联气体问题
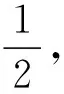
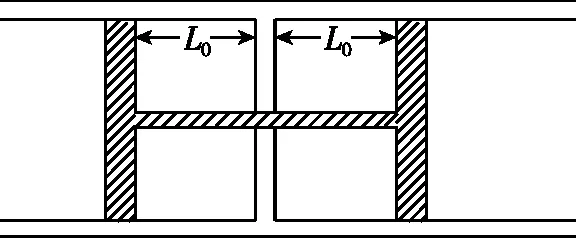
图4
(ⅰ)此时上、下部分气体的压强;
(ⅱ)“H”形连杆活塞的质量(重力加速度大小为g)。
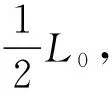
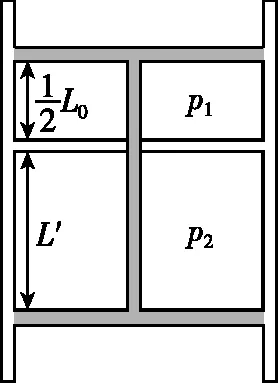
图5
第一步曲——分别对各部分理想气体列出理想气体状态方程
题中说明“整个过程温度保持不变”,所以两部分气体均发生等温变化,根据玻意耳定律
①
②
第二步曲——列出压强关联方程
对竖直放置的“H”形活塞进行受力分析,列出平衡方程
p1S=mg+p2S
③
第三步曲——列出几何关联方程
由于“H”形活塞内的气体总体积不变,所以根据几何关系可得
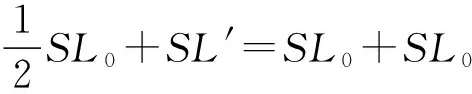
④
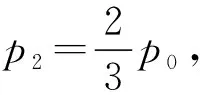
二、“液柱类”关联气体问题
【例4】[2018·全国Ⅲ卷·33(2)]如图6,在两端封闭、粗细均匀的U形细玻璃管内有一股水银柱,水银柱的两端各封闭有一段空气。当U形管两端竖直朝上时,左、右两边空气柱的长度分别为l1=18.0 cm和l2=12.0 cm,左边气体的压强为12.0 cmHg。现将U形管缓慢平放在水平桌面上,没有气体从管的一边通过水银逸入另一边,求U形管平放时两边空气柱的长度。在整个过程中,气体温度不变。
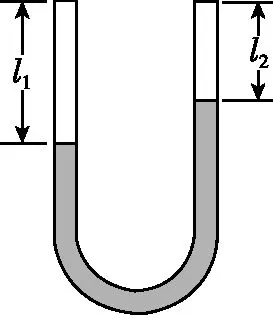
图6
【试题分析】左右两段定质量气体,通过汞柱构成“关联气体”。设U形管两端竖直朝上时,左、右两边气体的压强分别为p1和p2。U形管水平放置时,两边气体压强为p1′ 和p2′ ,此时原左、右两边气体长度分别变为l1′ 和l2′ 。如图7所示。
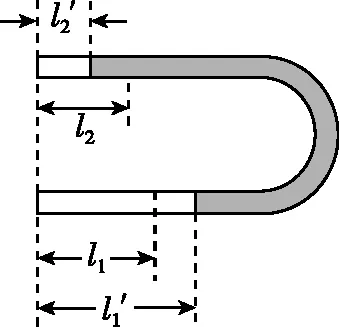
图7
第一步曲——分别对各部分理想气体列出理想气体状态方程
由题中条件“在整个过程中,气体温度不变”可知管中气体发生等温变化,根据玻意耳定律
对左边气体p1l1=p1′l1′
①
对右边气体p2l2=p2′l2′
②
第二步曲——列出压强关联方程
开始时,根据力的平衡条件
p1=p2+ρg(l1-l2)
③
U形管水平放置时,两边气体压强相等
p1′ =p2′
④
第三步曲——列出几何关联方程
由于管长不变,水银柱长度也不变,所以两段气体的总长度(体积)不变,由几何关系得
l1′ -l1=l2-l2′
⑤
联立①②③④⑤式得l1′ =22.5 cm,l2′ =7.5 cm
三、解题策略总结
关联气体问题因其研究对象多且相互联系,一直都是学生学习的难点,本文提出的解题“三步曲”可以有效地帮助学生形成严谨有条理的解题思路。通过以上几道高考真题,不难发现,在应用解决关联气体问题的“三步曲”时应当注意以下几个方面:
第一步曲,对各部分理想气体分别列出理想气体状态方程时要先准确判断出气体发生怎样的变化,这样才能选择正确的气体实验定律来列出方程。例如“导热缸壁”或“玻璃管”+“环境温度不变”,就说明气体发生等温变化,应该选择玻意耳定律。在列方程的时候,要大胆设出压强、体积、长度等未知参量,这些参量在第二、三步曲的方程中都可以被使用。
第二步曲,列出压强关联方程实际上就是平衡方程。对活塞类问题来说,应当把活塞作为研究对象,根据力的平衡条件,判断出活塞两侧的关联气体的压强关系,计算时要注意活塞的质量是否考虑。对液柱类问题来说,应当把汞柱作为研究对象,根据力的平衡条件,判断出与汞柱两液面接触的关联气体的压强关系,解题时用cmHg作为单位可以简化运算。

