平抛运动问题的归类解法与技巧

胡道成

(贵州省毕节第三实验高级中学)

平抛运动是一种重要的曲线运动,解决平抛运动问题是在“化曲为直”思想的指导下,将平抛运动分解为水平方向的匀速直线运动和竖直方向的自由落体运动,是“合成与分解法”这一重要物理方法的具体应用。平抛运动问题与生产生活和现代科技结合得非常紧密,能够承载“情境问题”,内容还涉及牛顿运动定律及“等效思想”的应用,对考查学生的理解能力、推理论证能力、模型建构能力和“能量观念”具有不可替代性,也就成了高考命题的热点。做平抛运动的物体在运动过程中往往会受到几何条件的约束,因此,解题策略上要按落点情况进行归类,解题方法上要以“速度正交分解法或位移正交分解法”为突破口,解题技巧上要以求时间为桥梁,结合等时性、三角函数关系、勾股定理、相似三角形等知识来解决问题,形成结构化、程序化的知识结构体系至关重要。

一、物体落点在竖直面上,水平位移决定时间

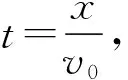
【例1】如图1所示,玩具射击枪水平放置,枪与目标靶中心位于离地面足够高的同一水平线上,枪口与目标靶之间的距离为x=100 m,子弹射出的水平速度v0=100 m/s,子弹从枪口射出的瞬间目标靶由静止开始释放,不计空气阻力,重力加速度g=10 m/s2。

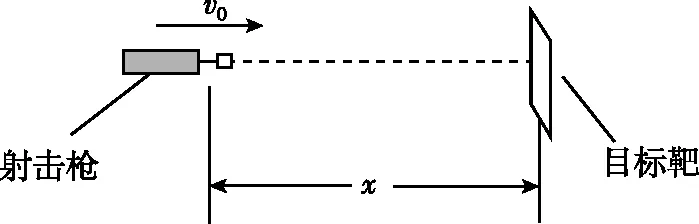
图1

(1)求子弹从射出到击中目标靶的时间t;

(2)求目标靶从释放到被子弹击中下落的高度h。

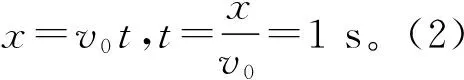
【点评】解题过程就是寻找等量关系的过程,本题中子弹恰好击中目标靶,说明子弹和目标靶的运动时间上相等,空间上下落高度相等,据此列出等式即可求解。

二、物体落点在水平地面上,竖直位移决定时间

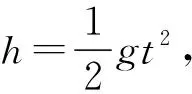
【例2】如图2所示,x轴在水平地面上,y轴在竖直方向。图中画出了从y轴上不同位置沿x轴正向水平抛出的三个小球a、b和c的运动轨迹,小球a从(0,2L)抛出,落在(2L,0)处;小球b、c均从(0,L)抛出,分别落在(2L,0)和(L,0)处。不计空气阻力,下列说法正确的是 ( )

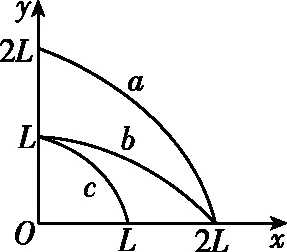
图2

A.a和b的初速度相同

B.b和c的运动时间相同

C.b的初速度是c的2倍

D.a的运动时间是b的2倍

【答案】BC

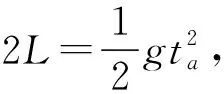
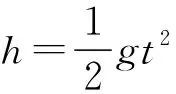
三、物体垂直打在斜面上,分解速度突破

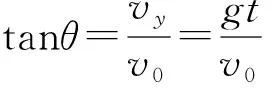
【例3】如图3所示,长木板OA的倾角θ=30°,在O点正上方的P处水平抛出一个小球,结果小球恰好垂直打在板面上距离O点为L的B点。重力加速度大小为g,空气阻力忽略不计。下列说法正确的是 ( )

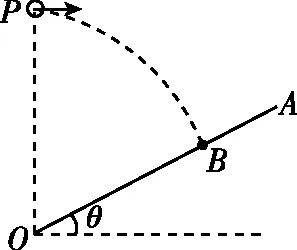
图3

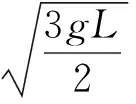
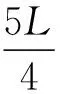
【答案】BD

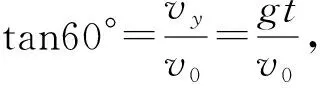
【点评】对于物体垂直打在斜面上的情形,分解末速度是解题突破口。本题未给出初速度,先由几何关系找出小球水平位移和竖直位移,通过分解小球在B点的速度,根据几何关系找出小球初速度与时间的关系即可求出时间,以此为桥梁又可求出小球打在B点的速度,再由几何关系求出O、P两点间的距离。

四、物体从斜面顶端抛出落到斜面上,分解位移突破

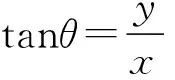
【例4】高山滑雪是2022年北京冬奥会的比赛项目之一。如图4所示,假设两名高山滑雪运动员a、b(均可视为质点)从雪道末端先后以初速度之比va∶vb=1∶3沿水平方向向左飞出,不计空气阻力,两名运动员从飞出至落到雪坡上的整个过程中,下列说法正确的是 ( )

图4

A.他们飞行的时间之比为3∶1

B.他们的水平位移之比为1∶3

C.他们落到雪坡上的瞬时速度方向不相同

D.他们在空中离雪坡的最大距离之比为1∶9

【答案】D

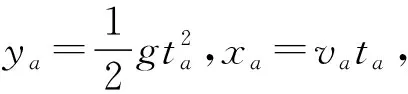
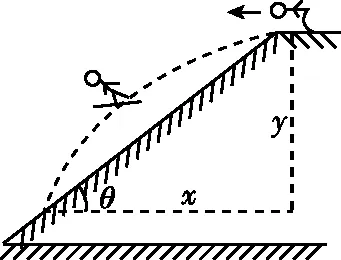
图5

【点评】对于滑雪这类体育运动中的平抛运动问题,构建平抛运动模型往往是解决问题的基础。本题中的运动员从雪坡上端水平飞出后落到雪坡上,识别出“斜面+平抛运动”模型后,通过分解位移就能找到求解时间的突破口,进而结合几何关系和平抛运动规律进行解答;对于“求物体离斜面的最大距离”的问题,则用“物体垂直于斜面方向上的分速度为零时,物体离斜面的距离最大”来解决。

五、物体落点在曲面凹侧或凸侧,轨迹与曲面相切,通过“角度关系”来突破

物体落在曲面凹侧或凸侧,并与曲面相切的问题,解题的突破口在于充分利用末速度与曲面相切的特点,分解末速度,再用竖直速度求出运动时间,往往问题就能迎刃而解;对于末速度与曲面不相切的问题,则要用分解位移的方法来求解;对于物体平行于斜面方向进入斜面上的问题,也是根据瞬时速度方向与斜面方向平行的几何关系,通过分解速度来进行求解。

【例5】如图6所示,圆弧形凹槽固定在水平地面上,其中ABC是位于竖直平面内以O为圆心的一段圆弧,OA与竖直方向的夹角为α,一小球以速度v0从桌面边缘P水平抛出,恰好从A点沿圆弧的切线方向进入凹槽。小球从P到A的运动时间为________,直线PA与竖直方向的夹角β为________。

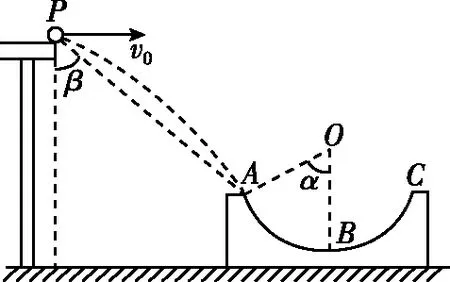
图6

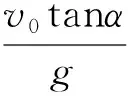
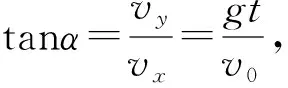
【点评】本题的解答过程中,抓住小球沿切线方向进入曲面这个条件,通过连接落点和圆心,由几何关系找出分解速度所需的角度,利用三角函数关系求出运动时间,然后分解位移来寻找位移偏向角与速度偏向角之间的关系,从而使问题得以解决。对于小球做平抛运动与曲面不相切的问题,则需要分解位移,且落入曲面高度相同的情况下,可能会有两个不同的水平位移,需要注意多解问题。

【例6】如图7所示,ab为竖直平面内的半圆环acb的直径,c为环上的最低点,环半径为R。将一个小球从a点以初速度v0沿ab方向抛出,重力加速度为g,不计空气阻力。则 ( )

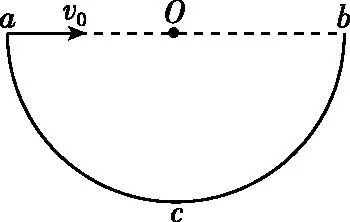
图7

C.当小球的初速度v0取适当值时,小球可以垂直撞击圆环

D.小球的初速度v0不同,撞击到环上的运动时间可能相同

【答案】AD

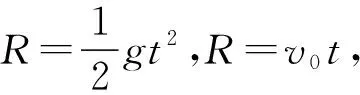
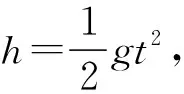
六、物体落在边界范围内的临界问题,求时间突破

平抛运动的临界问题主要是球类不触网也不出界问题、小物体落入容器问题或穿越矩形孔问题之类的“受限”问题,解决问题的基本思路是将实际问题转化为物理模型,利用平抛运动的轨迹,根据几何关系寻找水平速度、竖直速度、水平位移、竖直位移等临界条件,结合平抛运动的分解方法和基本规律进行求解。

【例7】乒乓球发球机是一个很好的辅助练习者练球的工具。如图8所示的乒乓球桌面ABCD的AB边长为L1,BC边长为L2,球网GIJK竖直放置于桌面的正中间,网高为h;发球机简化为EF,其中E点固定在AB边的中点,F点为乒乓球发射点,EF始终保持竖直,高度为H(可调)。乒乓球看成质点,每次均从F点水平发射,发射方向可以在水平面内任意调整,不计空气阻力和周围环境对乒乓球运动的影响,也不考虑乒乓球旋转,当球擦网而过时,则下列说法正确的是 ( )

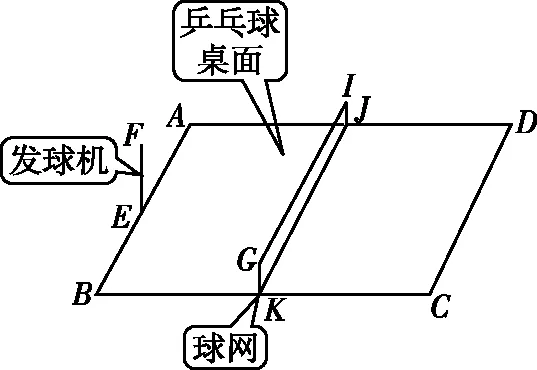
图8

C.只要H大于h,就一定能设置合适的发球速率,使球落在JKCD区域内

D.若球以垂直于AB边的方向发射能够擦网而过后直接落到CD边界上,则适当调整发射速度后,只要是落在CD边界上的球一定是擦网而过的

【答案】D

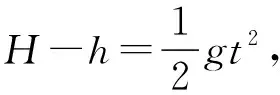
【点评】由于高度决定了时间,水平位移由初速度和高度决定,因而乒乓球可能会出现恰好过网或恰好不出界的临界状态。解决这类问题的关键是确定临界状态：一是发球速率较小时,乒乓球刚好沿中心线擦着球网上边缘而落到球网右侧桌面上;二是发球速率较大时,乒乓球刚能落在球网右侧桌面上,且落点在桌角处。处理这类临界问题需要认真观察具体情境,充分发挥空间想象能力,学会换个视角看情境(侧视、俯视),顺利识别出情境中的物理模型至关重要。

七、物体落在圆盘上的组合问题,求时间突破

做平抛运动的物体落在做圆周运动的物体上这类组合问题,需要利用竖直位移决定时间,求出时间作为解题的纽带,将水平位移与落点的半径联系起来,要注意的是圆周运动的周期性运动可能会导致出现多解。

【例8】如图9所示,M是水平放置的半径足够大的圆盘,绕过其上表面圆心的竖直轴OO′匀速转动,以经过圆心O水平向右的方向作为x轴的正方向。在O正上方距盘面h处有一个正在间断滴水的容器,该容器从t=0时刻开始随传送带沿与x轴平行的方向做匀速直线运动,速度大小为v。已知容器在t=0时滴下第一滴水,以后每当前一滴水刚好落到盘面上时再滴一滴水。

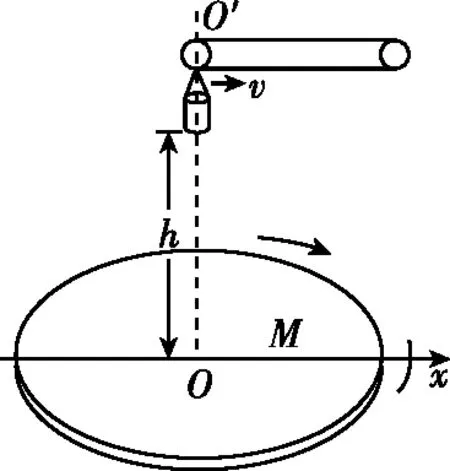
图9

(1)每一滴水经过多长时间落到盘面上;

(2)要使每一滴水在盘面上的落点都位于一条直线上,求圆盘转动的最小角速度ω;

(3)求第二滴水与第三滴水在盘面上的落点间的最大距离s。

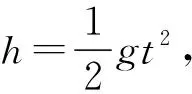
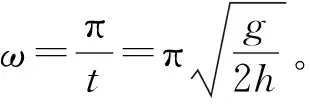
【点评】对于平抛运动与圆周运动的组合问题,解题突破口都是用时间作为桥梁,需要用“侧视”和“俯视”来观察两个运动过程的具体情景,注意周期性导致的多解,尤其要弄清待求量是圆盘转过nπ还是2nπ的情形,还要确定n的取值范围;若涉及极值问题,则寻找极值条件是个难点,要善于画出示意图来分析。

八、物体落在“函数面”上,用曲线方程突破

平抛运动物体与圆面、椭圆面、抛物面等的“邂逅”问题,抛体运动的落点位置必然与这些曲面对应的函数产生联系,落点的位置坐标一定满足对应的曲线方程,且落点与抛出点之间的水平和竖直位移又满足平抛运动基本规律,实现了物理规律与曲线方程、数学方法的完美组合。

【例9】如图10所示,一个质量为0.4 kg的小物块(可视为质点)以v0=1 m/s的初速度从水平台上的O点水平飞出,击中平台右下侧挡板上的P点。现以O为原点在竖直面内建立如图所示的平面直角坐标系,挡板的形状符合方程y=x2-6(单位：m)的曲线,不计一切摩擦和空气阻力,重力加速度g=10 m/s2,则下列说法正确的是 ( )

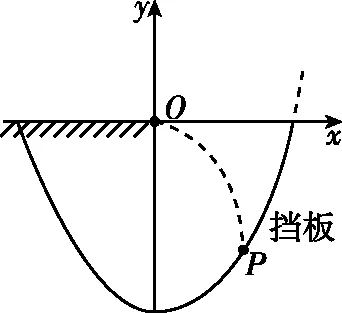
图10

A.小物块从O点运动到P点的时间为1 s

B.小物块刚到P点时瞬时速度方向与水平方向夹角的正切值等于5

C.小物块刚到P点时速度大小为10 m/s

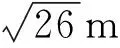
【答案】AD

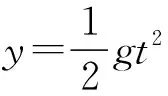
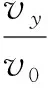
【点评】处理平抛运动物体与圆面、椭圆面、抛物面等“函数面”结合的问题,抓住抛体运动的落点位置坐标一定满足对应的曲线方程,且抛体(质点)的运动过程也满足平抛运动基本规律,结合起来就能找到解决问题的方法。值得一提的是有些问题里的“抛出点”与函数方程的“原点”并不重合,这时还要将落点的位置坐标进行适当变换才满足曲线方程,代入数据计算时要倍加小心。