活用多边形外心确定多面体外接球的球心
2023-08-09黄雨顾飞
黄 雨 顾 飞
(安徽省淮南第二中学)
球是高中立体几何中非常重要的几何体之一,也是最优美的空间几何体之一.古希腊数学家阿基米德的墓碑上刻着球及其外接圆柱,这是其最得意的图形,可见球是受到了大数学家的青睐.关于空间几何体外接球和内切球的问题,是高中数学学习的一个难点.为了有效解决这一问题,一线数学教师构建了很多模型来解决球的问题,例如,墙角模型、汉堡模型、斗笠模型、切瓜模型等,通过构建不同的模型解决各种球的问题,但是模型太多,方法太杂.
1.知识背景
1.1 球的性质
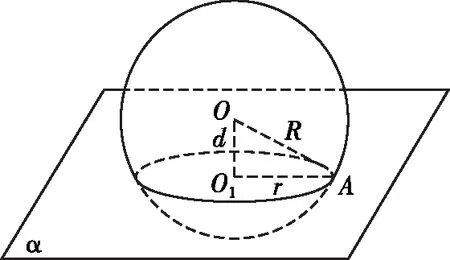
性质1:用一个平面去截球,其截面图形是圆;
性质2:球心与截面圆圆心的连线垂直于截面;
性质3:球的半径为R,截面圆的半径为r,球心到截面圆圆心的距离为d,则R2=d2+r2(如图).
1.2 三角形外接圆
外接圆圆心:三角形三边中垂线的交点即是三角形外接圆圆心,简称外心.

2.知识深化
由性质1可知,O1就是多边形的外心.
由性质2可知,OO1⊥平面O1,反过来,过O1且垂直于平面O1的直线一定经过球心O.那么,我们选取两个截面,分别过两个截面的圆心O1,O2,作各自平面的垂线,则这两条垂线的交点就是球心O,如图1.

图1
凝练:选取多面体的两个平面,找两个面多边形的外心,分别过两面多边形的外心作各自面的垂线,两垂线的交点是球心.
特殊情况:
推论一:如图2,如果两面多边形的外心重合,那么这个外心就是球心.

图2
推论二:如图3,如果过一个面外心的垂线经过另一个面的外心,那么另一个面的外心就是球心.

图3
3.知识运用
3.1 特殊情况1
【例1】中国古代数学专著《九章算术》系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的三棱锥称之为鳖臑.如图为一个阳马与一个鳖臑的组合体,已知三棱锥P-ADE为鳖臑,且PA⊥平面ABCE,AB=AD=2,ED=1,该鳖臑的外接球的表面积为9π,则阳马的外接球的体积为
( )


【答案】D



【注】本题满足推论一,可以直接确定球心的位置.

( )

A.5π B.13π C.6π D.14π
【答案】A
【解析】由题意得△PAB,△PCB均为直角三角形,则外心均为PB的中点,故PB即为三棱锥P-ABC的外接球的直径.
设PA=a,PC=c,

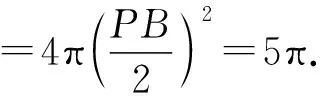

3.2 特殊情况2
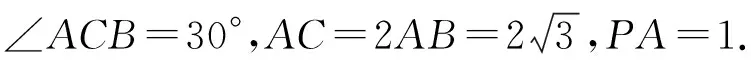
( )


【答案】D


【注】本题满足推论二,过一个平面的外心O1的垂线经过另一个平面的外心O,这个外心O即为球心.特别注意,作平面的垂线一定要有参考线,本题参考线是PA.
【例4】(2021·A10联盟高二上学期开学联考)如图,在几何体ABCDEF中,底面ABCD是正方形,EF∥平面ABCD,EF=4,其余棱长都为2,则这个几何体的外接球的体积为
( )


【答案】D


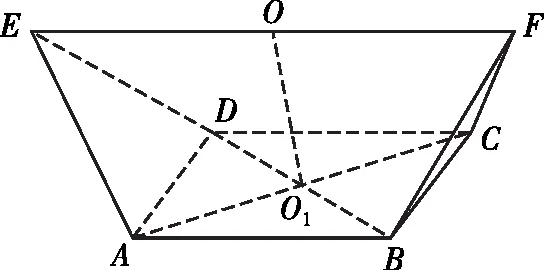
【注】本题可以采用两种特殊情况来快速解决,也可以采用一般情况来解决,下文我会详细介绍一般情况的解决方法.等腰梯形、正方形的外心也是我们所熟知的内容,要根据边长关系确定其外心的位置.
3.3 一般情况
对于一般情况,需要确定两个平面多边形的外心,过外心分别作各自平面的垂线.那么这两个面的选取要有可行性,要能确定其外心及垂线的位置.
( )
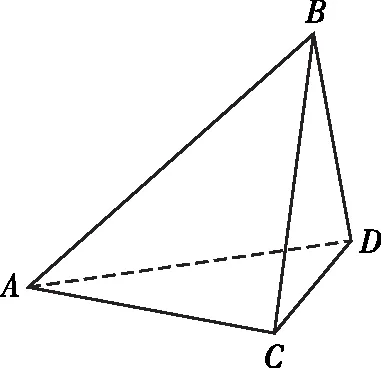

【答案】A
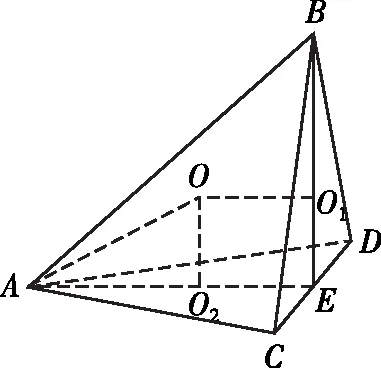
【注】选取的两个平面图形要满足两个条件,一是能够确定外接圆圆心的位置及半径,二是作垂线时要找到与平面垂直的直线作为参考线,这样作出的垂线才能求解.本题称为切瓜模型,我们抛开模型,从球的性质出发,仍能很好地解决.
【例6】(《立体几何的秘密》 苏立标 编著)如图,已知正方形ABCD的边长为4,E,F分别是AB,BC的中点,将△ADE,△EBF,△FCD分别沿DE,EF,FD折起,使得A,B,C三点重合于点A′.若点G及四面体A′DEF的四个顶点都在同一个球面上,则以△FDE为底面的三棱锥G-DEF的高h的最大值为
( )
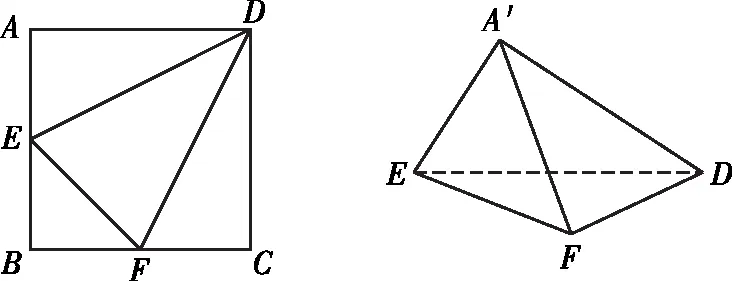


【答案】A
【解析】解法一:设外接球的球心为O,球的半径为R,折叠后满足墙角模型.
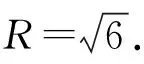

解法二:如图,过△A′EF的外心O1作A′D的平行线,过△A′DF的外心O2作A′E的平行线,两线交于点O,点O即为外接球球心.
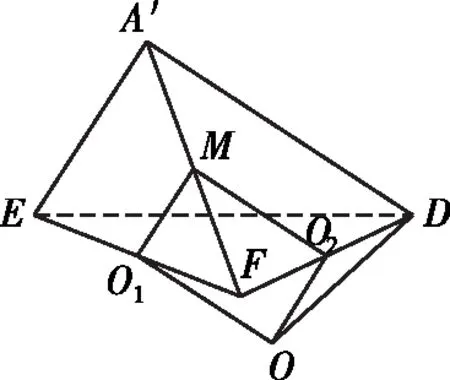
【注】本题可用墙角模型来解决.我们也可以抛开模型,就从球的基本性质出发,牢牢抓住本质,反而更有利于学生对知识的理解.
4.知识总结
4.1 淡化模型教学,注重知识本质
立体几何的教学离不开实物或模型,空间想象也不是凭空产生的,都是在实物或模型的基础上抽象出来的.但是我们不能只认识实物或模型,实物或模型总是有限的,而空间几何体是无限的、千变万化的.要使同学通过对有限实物或模型的观察、体验,抽象出对于一般几何图形的空间观念.
模型化的解题通常是一题一法,不利于学生对知识本质的理解,教师教学中一定要抓住球的本质属性,强调通性通法,力求用最本质的方法解决更多的问题.
4.2 平面多边形的选取一定要有可行性
第一,选取的平面多边形的外心能够确定位置.可以选取直角三角形、等边三角形等特殊多边形,如果是一般三角形,可以选取边角等元素已知的三角形,方便确定外接圆圆心的位置.

(本文系2021年度安徽省教育科学研究项目《基于数学实验课程建设下的高中生数学学习品质的培养与评价研究》编号(JK21099)的阶段性研究成果)
