2023届高考仿真试卷(新高考全国卷)

李鸿昌

(北京师范大学贵阳附属中学)

第Ⅰ卷(选择题 共60分)

一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.

1.已知集合A={x|x2-4≤0},B={x|log2x<1},则A∩B=

( )

A.∅ B.[-2,2)

C.(0,2] D.(0,2)

( )

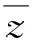
A.第一象限 B.第二象限

C.第三象限 D.第四象限

( )

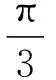
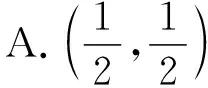
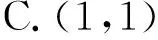
4.数学家希尔伯特在1900年提出了孪生素数猜想:存在无穷多个素数p,使p+2是素数.当p和p+2都是素数时,称素数对(p,p+2)为孪生素数.那么从3到43这41个整数中随机取2个不同的数,则这2个数是孪生素数的概率为

( )

( )

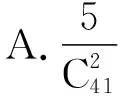
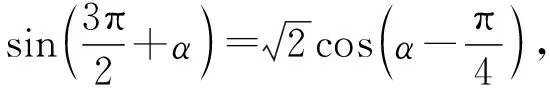
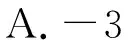
6.已知圆台上底面半径为1,下底面半径为3,球与圆台的两个底面和侧面均相切,则该圆台的侧面积与球的表面积之比为

( )

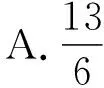
7.2010年,考古学家对良渚古城水利系统中一条水坝的建筑材料(草裹泥)上提取的草茎遗存进行碳14年代学检测,检测出碳14的残留量约为初始量的55.2%,据此推测水坝建成的年代是

( )

(参考数据:碳14的半衰期为5 730年,log25≈2.322,log269≈6.108 5)

A.公元前2850年

B.公元前2880年

C.公元前2904年

D.公元前2920年

8.已知a=1012,b=1111,c=1210,则a,b,c的大小关系为

( )

A.a

C.b

二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.

9.某地为相应“扶贫必扶智,扶智就是扶知识、扶技术、扶方法”的号召,建立了农业科技图书馆,供农民免费借阅,收集的自2017年至2021年共5年的年借阅数据如表:

年份20172018201920202021年份代码x12345年借阅量y(万册)2173693142

( )

A.a=4

B.2,17,36,93,142的第三四分位数为93

C.此回归模型第2020年的残差(实际值与预报值之差)为5

D.估计2022年借阅数为220

10.设正方体ABCD-A1B1C1D1的棱长为1,P为线段A1D上的一个动点,下列结论正确的是

( )

A.BP⊥BC

B.BP∥平面CB1D1

11.已知定义在R上的偶函数f(x)满足f(1-x)+f(1+x)=0,且对任意的x∈R,导函数f′(x)均存在,则

( )

A.f(x)的图象关于点(1,0)对称

B.f′(x)的图象关于原点对称

C.f(2 023)=0

D.∀x∈R,f′(x+2)=f′(x)

( )

B.|AF2|=3|F2C|

C.AB⊥BC

第Ⅱ卷(非选择题 共90分)

三、填空题:本题共4小题,每小题5分,共20分.

13.已知(1+x)(x-ay)5的二项展开式中x3y3的系数为80,则a=________.

15.已知抛物线C:y=4x2,若圆M过C的顶点且在C内部,则圆M的半径的最大值为________.

16.设直线y=kx+b是曲线y=lnx+1的切线,也是曲线y=ln(x+2)的切线,则b=________.

四、解答题:本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.

17.(10分)已知数列{an}的前n项和为Sn=n2+1.

(Ⅰ)求{an}的通项公式;

(Ⅰ)如图进行一次高尔顿板试验,求小球落入5号球槽的概率;

(Ⅱ)五一期间,某商场门口利用如图中的高尔顿板举行游戏活动,顾客只要花51元就能一次玩高尔顿板游戏.一次游戏中小球掉入X号球槽得到的奖金为ξ元,其中ξ=|100-20X|.

(ⅰ)求X的分布列和期望E(X);

(ⅱ)高尔顿板游戏活动火爆进行,很多顾客参加了游戏活动,你觉得商家能盈利吗?

图1

图2

(Ⅰ)当λ为何值时,BF⊥PD;

(Ⅰ)求C的方程;

(Ⅱ)设P为C右支上的动点,在x轴负半轴上是否存在定点M,使得∠PFM=2∠PMF?若存在,求出点M的坐标;若不存在,请说明理由.

(Ⅰ)求实数a的取值范围;

关注“教学考试杂志”订阅号,后台发送“3期解析”,获取本卷详解详细.