一道正八面体试题的命制
2023-08-09吴晓明
教学考试(高考数学) 2023年3期
吴晓明
(福建省莆田第一中学)



图1
下面通过四个方法来解答.
解法一:设△ABC,△A1B1C1的中心分别为O,O1,取BC,B1C1的中点D,D1,过点D1作D1E⊥AD交AD于点E,如图2.∵OO1⊥平面ABC,∴OO1⊥AD,∴四边形EOO1D1为矩形,∴ED1=OO1,

图2

解法二:将该正八面体放置于正方体PQRS-P1Q1R1S1内,使得正八面体ABC-A1B1C1的每个顶点为正方体每个表面的中心,如图3,
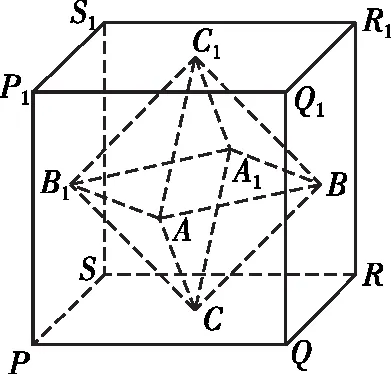
图3

图4

解法三:取BC的中点E,连接AE,A1E,过点A1作A1G⊥AE交AE的延长线于点G,如图5.

图5
∵平面ABC∥平面A1B1C1,
∴两平面的距离可化为点A1到平面ABC的距离,设为h.又∵正八面体ABC-A1B1C1是对称的,∴A1G⊥平面ABC,

图6

解法四:∵平面ABC∥平面A1B1C1,
∴两平面的距离可化为点A1到平面ABC的距离,
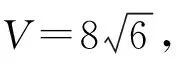
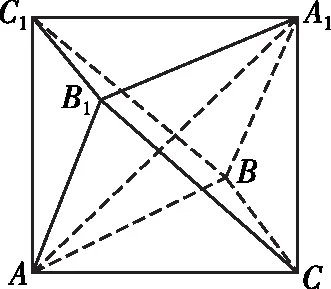
图7



(本文系福建省教育科学“十四五”规划2021年度立项课题《基于核心素养的高中数学探究性学习实践与研究》课题编号(FJJKZX21-283)的阶段性研究成果)
