均值换元法解题研究

山东省寿光市教育科学研究中心(262700) 张明同 李佩龙

山东省寿光二中(262700) 刘海云

均值换元法是指借助于几个值的平均值进行换元的方法,如若a1+a2+...+an=m(n∈N,n≥2),则可设

其中λ1+λ2+...+λn= 0,这就是均值换元. 应用均值换元法解题,可以降低解题难度,简化解题过程,达到事半功倍的效果. 本文对均值换元法解题进行研究,希望能为读者提高解题能力提供帮助.

1. 均值换元法解题的切入点研究

利用均值换元法解题的关键是找到类似a+b=m的信息,然后进行均值换元,从哪里寻找可以进行均值换元的核心信息? 可以从以下三个方面考虑.

1.1 从题设中寻找有效信息

1.2 从未知结论中寻找有效信息

1.3 从题目挖掘隐含的有效信息

例3若函数f(x) = sin(x+φ)+cosx的最大值为2,则常数φ的一个值为____.

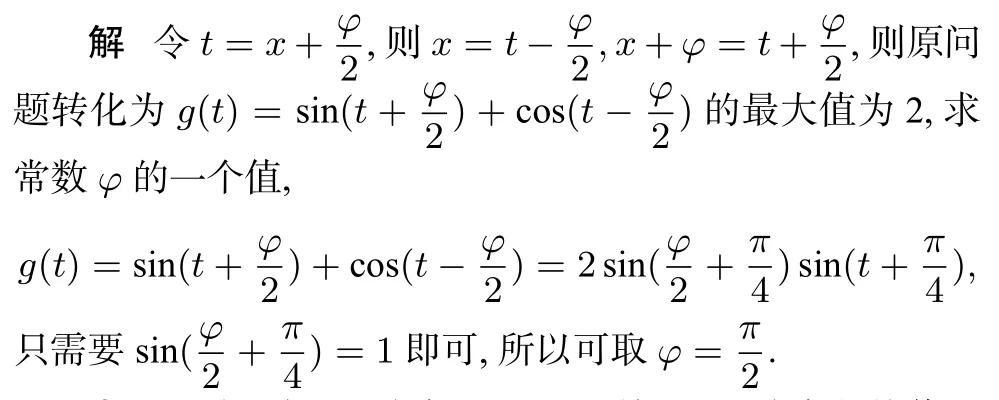
点评题目涉及两个角x+φ,x,利用这两个角的均值进行换元,使问题解答更轻松. 当题目中不存在类似a+b=m这样直接使用可进行均值换元的条件时,可以主动对条件进行分析和挖掘,寻找使用均值换元的条件,择机使用均值换元.

2. 均值换元法解题的题型研究

应用均值换元法解题的关键是要从题设及所求解题目的结构特征入手,挖掘出问题中隐藏的均值关系,从而使用均值换元法达到轻松解题的目的[1]. 均值换元法的应用非常广泛,下面进行举例分析.

2.1 证明等式

2.2 证明不等式

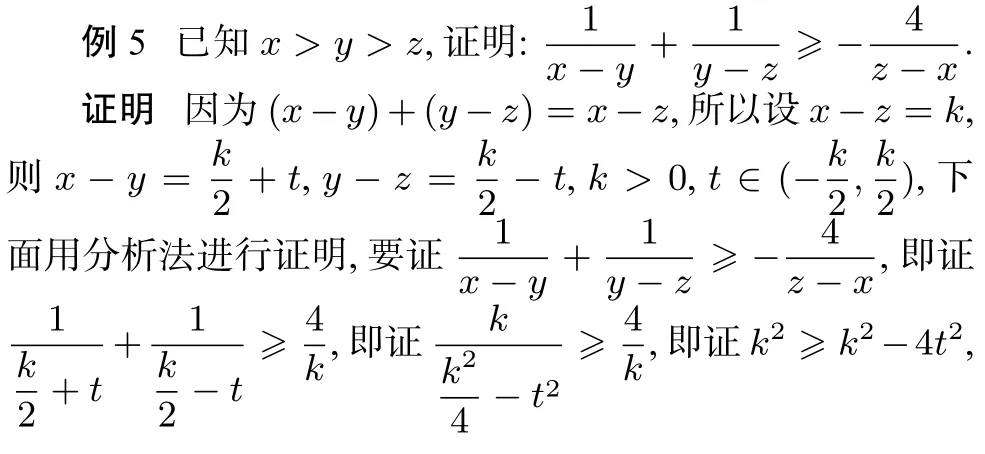
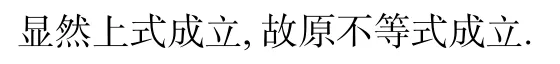
点评对题目中的信息进行变形,创造使用均值换元的条件,揭示量与量之间的不等关系的本质,可以达到使用均值换元的目的.

2.3 求范围(最值)

例6已知x,y∈ [0,+∞),2x+y= 6, 求z=4x2+3xy+y2-6x-3y的最值.

点评如果采用一般的思维方式,解题过程会相当繁杂,采用均值换元后,问题轻松解决,显示出均值换元的实力.

2.4 求值

2.5 解方程

例8 在实数范围内解方程(x+2)4=82-(x+4)4.

解设, 则x+ 2 =t-1,x+4=t+1,原方程变为(t-1)4+(t+1)4=82,展开并整理得,t4+6t2-40 = 0,解得t2= 4 或t2= -10(舍去负值),所以x1=-1,x2=-5.

点评如果将原方程直接展开会相当繁琐,经过均值换元后方程变为(t-1)2+(t+1)2= 82,变形后的方程展开后会有很多项相互抵消,简化了运算过程,显现出均值换元的优势.

从以上几个例题可以看出,“均值换元”的确是求解数学问题的一种非常有效的手段, 其本质原因是它变更了命题,而新命题更便于求解[2].