冷却模式对NM400相变塑性及残余应力的影响

方玉　丁文红　鲁小轩 梁亮　汪净 彭冲

关键词：冷却模式；耐磨钢；连续冷却；残余应力；相变塑性

0 前言

针对某厂热轧带钢连续冷却过程中采取的2种冷却模式（一种是全程快冷，一种是前置式超快速冷却+空冷）而造成的板形差异问题，本文以耐磨钢NM400为研究对象，通过热模拟试验、基于断裂力学原理的裂纹柔度法以及建立ABAQUS有限元仿真模型，弄清了NM400在连续冷却过程的相变行为以及冷却速度对其相变行为的影响规律，为改善NM400连续冷却过程残余应力水平及分布、减少板形缺陷提供了数据基础和理论依据。

1 试验材料及方法

1.1 试验材料

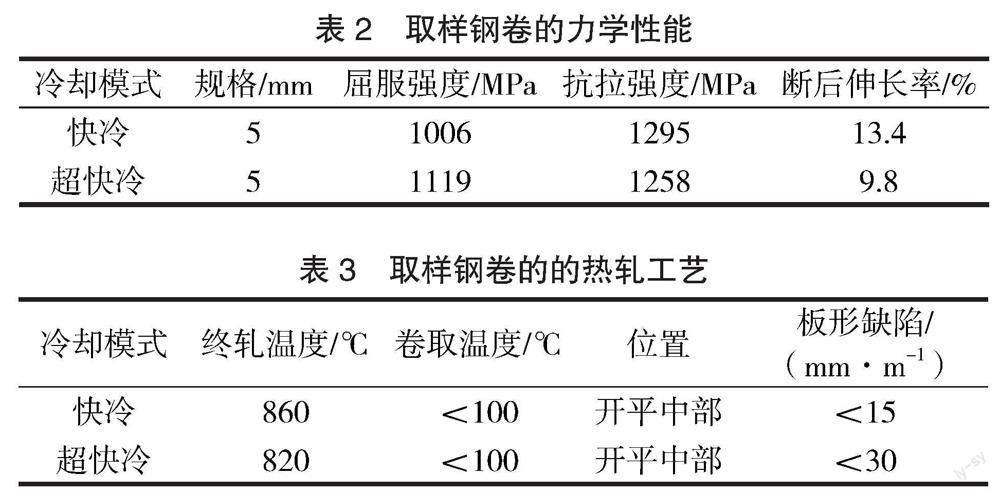
试验材料来自国内某厂生产的耐磨钢NM400，厚度为5 mm，宽度为1 500 mm，其化学成分、力学性能及轧制工艺参数分别见表1～表3。NM400在轧后冷却过程中采取了2种冷却模式：快冷和超快冷。快冷是通过控制冷却水阀门的开启密度，减少带钢表面积水，从而改善带钢的不均匀冷却。超快冷与传统的冷却工艺相比，冷却速度可达到常规冷却的2～5倍。本文涉及到的超快冷为前置式（前置式超快冷设备安装在层流冷却设备之前）。

1.2 试验方法

1.2.1 残余应力测试

从现场2种热轧工艺的钢卷上，沿带钢宽度方向从操作侧开始以带钢宽度1/2为对称中心，各取9个测试点作为残余应力测试样，共18块测试样（100 mm×90 mm）。通过前期课题组开发的裂纹柔度法实测2种冷却模式下的残余应力，裂纹柔度法的测量原理是在被测物体的表面引入一条深度逐渐增加的裂纹来释放残余应力，通过测量特定点的应变值来计算残余应力。

1.2.2 连续冷却过程的相变动力学及相变塑性试验

从其他厚度规格的成品钢板上沿轧制方向取中部材料，加工成直径为?6 mm×10 mm的试样。将试样装入Gleeble3500热模拟试验机后抽真空，并充入氩气以减少氧化。随后以100℃/s的升温速率将试样加热至1 000℃，保温5 min。然后以1℃/s的冷却速度将试样冷却至950℃，并在该温度下保温10 s，进行第一道次压缩变形，变形量ε=30%，变形速率ε为1s-1；首道次压缩完成后，以1℃/s的冷却速度将试样冷却至860℃，保温10s，同时进行第二道次压缩变形，变形量ε=30%，变形速率ε为1s-1，双道次压缩完成后，再分别以20、30、40、45℃/s的冷却速度将试样冷却至室温；第二道次压缩完成后，再分别以20、30、40、45℃/s的冷却速度将试样冷却至480℃（相变点以上50℃），对试样进行快速加载（1 s内完成加载），加载载荷分别为：-45、-60、-80MPa，保持上述载荷，并以加载前冷速冷却至室温。

1.2.3 ABAQUS子程序开发

根据模拟过程中的温度和NM400的相变动力学方程，使用USDFLD用户子程序计算马氏体的转变量及增量，将其作为状态变量存储在STATEV中，并传递给其他用户子程序HETVAL和UEXPAN。随后根据相变潜热计算公式，将马氏体相变产生的相变潜热作为内生热源，写入HETVAL子程序。通过以上步骤，可以计算出冷却过程中某一点的温度。最后，使用先前计算的温度作为预定义场，并输入与热相关的力学参数，通过编辑子程序UEXPAN计算热应变、相变应变与相变塑性应变，通过编写子程序UHARD考虑屈服强度的影响，得到最终的残余应力场。

2 结果与分析

2.1 试验结果与分析

2.1.1 裂纹柔度法测试结果

由2种冷却模式下各测点轧向残余应力沿厚度方向上的分布及应力偏差。可知，快冷时，靠近操作侧的A、B、C、D、E测点沿厚度方向上的轧向残余应力呈现大“U”形对称分布，靠近传动侧的F、G、H、I测点则呈现“W”形对称分布；而超快冷时各测点沿厚度方向上的轧向残余应力呈现“N”形不对称分布，超快冷时应力水平高。2种冷却模式下大部分测点轧向残余应力的偏差均小于该测点轧向残余应力绝对值的8%。超快冷时，A～I测点的下表面殘余应力分别为58.85、36.53、39.30、20.59、30.90、30.39、55.12、-114.36、110.72 MPa，上表面的应力分别为-294.38、-7.55、10.68、-172.01、-81.39、-66.26、-59.61、-108.93、-110.66 MPa。大部分测点上下表面应力状态为：一个受拉应力，一个受压应力，说明此时带钢上下表面延伸不一致，更容易在后续加工过程中产生由于上下表面应力非对称分布所导致的加工畸变。

2.1.2 冷却速度对NM400相变动力学的影响

热模拟相变动力学试验中，由不同冷却速度下NM400的组织。可知，当冷却速度为20℃/s时，组织中存在少量贝氏体，大部分为马氏体；当冷却速度在30℃/s以上时，全部为马氏体组织。

为了了解NM400连续冷却过程残余应力演变规律，掌握NM400转变进程至关重要。通过杠杆法以及修正后的K-M方程拟合可得到不同冷却速度下的相变动力学曲线和相变动力学方程。修正后的K-M方程见式（1）。

δ=1-exp[-α（Ms-t）n]（1）

式中：δ为马氏体转变量；α为相变动力学系数；Ms为马氏体相变开始温度；t为冷却过程中的温度；n为修正系数。

20℃/s：δ=1-exp[-0.02003×（393.34-t）1.1]（2）

30℃/s：δ=1-exp[-0.02740×（370.83-t）1.1]（3）

40℃/s：δ=1-exp[-0.02430×（363.22-t）1.1] （4）

45℃/s：δ=1-exp[-0.02993×（389.89-t）1.1] （5）

式（2）～式（5）为不同冷却速度下的相变动力学方程。

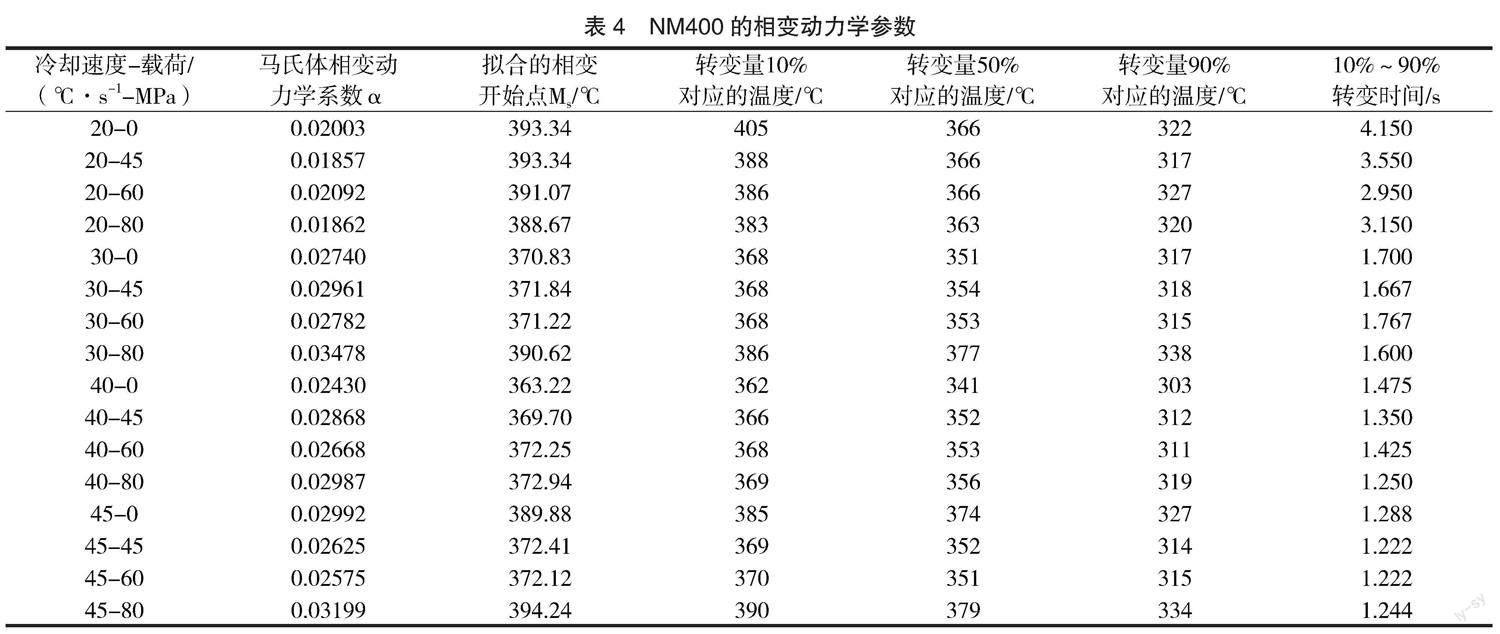
由不同冷却速度（20、30、40、45℃/s）下的马氏体相变开始温度分别为393.34、370.83、363.22和389.89℃，在冷却速度为20～40℃/s时，随着冷却速度的增加，相变开始点与结束点均降低；当冷速为45℃/s时，NM400的相变开始温度升高至389.89℃。不同冷却速度（20、30、40、45℃/s）下，马氏体转变10%～90%时间分别为4.150、1.700、1.475和1.288s，并且马氏体转变10%～50%所需的时间均小于马氏体转变50%～90%，即冷速增加，相变时间缩短，且马氏体前期转变远快于后期。在相变转变量小于80%时，NM400的相变速率近似恒定；当材料的转变量大于80%后，材料的相变速率明显降低。而且，冷却速度越大，相变后期相变速率降低的现象越显著。

2.1.3 应力对NM400相变动力学的影响

从表4可知，外加载荷对NM400相变动力学的影响相对较小，而冷却速度对NM400相变动力学的影响较为显著，且随着冷却速度的增加，NM400的相变时间近似呈线性减小。据此，可将相变动力学系数修正为式（6）。

α=0.0003v+0.01529（6）

式中：v为冷却速度。

随着冷却速度的增加，Ms点呈先下降、再上升的趋势，冷却速度为40℃/s时，Ms点达到极小值363.22℃。载荷对Ms点的影响未呈现出一致性规律，在本次计算中仅考虑冷速对相变开始点的影响，并表达为式（7）。

Ms=-0.75v+398（7）

从而得到考虑冷却速度影响的相变动力学方程式（8）。

δ=1-exp[-（0.003v+0.01529）×（-0.75v+398-t）1.1]（8）

2.1.4 NM400相变塑性研究

在较小的应力作用下会发生明显的相变塑性变形，压应力作用下产生的相变塑性应变均为负值，相变塑性应变与应力加载方向具有一致性。

根据Greenwood-John模型相变塑性一般可表示为

εtp=kσδ（9）

式中：k为相变塑性系数；σ为外加应力。

当马氏体相变结束后，即马氏体体积分数为1时，式（9）可以简化为式（10）。

εtp=kσ（10）

通过式（10）得到各个冷却速度（20、30、40、45℃/s）下的相变塑性系数k分别为8.9119×10-5、9.7734×10-5、9.1414×10-5和8.3259×10-5，随着冷却速度的增加，相变塑性系数先增大后减小。冷却速度在20℃/s时，存在少量的贝氏体组织，对马氏体相变塑性的计算过程中存在一定的影响，通过对冷却速度30℃/s以上的相变塑性系数k进行拟合，得到方程见式（10）。

k=1.2597×10-4-9.1740×10-7v（11）

在试验参数范围内，相变塑性应变随着加载应力的增加而近似线性增大；而冷却速度对相变塑性应变的影响相对较小。

2.2 模拟结果与分析

2.2.1 相变塑性对残余应力的影响

本文以5 mm×1 500 mm规格的NM400为例，通过修改UEXPAN子程序，将相变塑性应变当做一独立应变加入至本构方程中实现数值模拟，得到了相变塑性对残余应力的影响规律。

通过ABAQUS提取带钢表面与心部的应力数据可知第Ⅰ阶段：温度场驱动下的应力分布。NM400刚开始冷却时，表面受拉应力，心部受压应力，该应力影响初始相变塑性应变方向。

第Ⅱ阶段：表面相变驱动下的应力分布。当带钢NM400表面到达相变温度，开始相变。在相变应变影响下，带钢表面相变区域体积膨胀，随着相变转变量的增加，表面拉应力迅速切换为压应力，并带动心部应力由压应力切换为拉应力。由于相变塑性应变的方向与应力偏张量方向一致，因此，相变塑性应变也由初始的拉应变迅速切换为压应变。此时，相变塑性应变抵消部分相变膨胀应变的影响，抑制了残余应力的增长。所以，在这一阶段，考虑相变塑性應变时的应力显著低于不考虑相变塑性应变时的应力。

第Ⅲ阶段：心部相变驱动下的应力分布。当带钢NM400心部到达相变温度后，开始相变。在带钢心部相变应变的影响下，心部相变区域体积膨胀，使得由表面相变所导致的拉应力逐步减少。受应力的偏张量影响，此时带钢心部的相变塑性应变为拉应变，与相变应变的方向一致，因此，相变塑性应变与相变应变叠加，使心部应力迅速由拉应力切换为压应力，并带动表面应力由压应力切换为拉应力。当不考虑相变塑性应变时，应力变化的驱动力仅有相变应变，因此，不考虑相变塑性应变时，NM400残余应力的计算结果要小于实际值。

第Ⅲ阶段后的平稳阶段是心部相变结束后，带钢表面与心部应力趋于稳定。因此，相变塑性应变对残余应力的影响取决于相变时刻应力偏张量的方向及大小（相变塑性应变的大小与正负），直接影响着相变后带钢内的残余应力分布。

2.2.2 连续冷却过程残余应力的形成机制

本文重点讨论轧后的连续冷却过程，通过计算连续冷却过程的温度场、应变场和应力场探讨冷却模式对NM400残余应力影响的内在机制。

（1）温度场对比分析。

由不同冷却模式下的温度和温度差变化可知，快冷时，带钢厚度方向上的最大温差为28℃，而超快冷时，带钢厚度方向上的温差高达189℃，这意味着超快冷模式下，温度应力对相变行为的影响更为显著。

（2）应变对比分析。

由于在超快冷模式下带钢表面与心部温差大，且超快冷速下NM400的相变速率大，因此当带钢心部开始相变时，表面相变已经完成94%。而在快冷模式下，当带钢心部开始相变时，表面相变仅完成35%。导致超快冷模式下，带钢心部相变所产生的相变塑性应变远大于快冷模式下带钢心部相变所产生的相变塑性应变。

（3）残余应力对比分析。

导致超快冷模式下带钢应力水平高的主要原因是：带钢心部相变前，表面带钢相变体积分数过大，造成带钢心部相变时所受的拉应力过大，诱导心部带钢产生与相变应变同向的大相变塑性应变，因而在带钢内部造成高幅值的残余应力。

2.3 实测与模拟对比

本文建立的NM400残余应力预测模型，考虑了冷却速度对相变动力学及相变塑性的影响，以E测点为例，模拟与实测对比结果见表5。模拟与裂纹柔度法的实测结果数值存在差异，但均超快冷时应力水平较高。其主要原因如下：（1）裂纹柔度法的实测试样为开平加工后的，开平加工改变了带钢内部的残余应力分布规律，因此，模拟计算值必然与实测数据存在差异；（2）本文模拟的连续冷却过程是理想情况下的，未考虑卷取张力以及板形缺陷释放对残余应力的影响。

3 结论

（1）实测与模拟结果均表明，超快冷时应力水平较高。导致超快冷后带钢残余应力水平高的关键原因是：加大冷速后提高了带钢心部相变开始时带钢表面相变的体积分数。该体积分数越大，心部开始相变时所受到的拉应力水平越高，相变所产生的相变塑性应变越大。由于此时所形成的相变塑性应变与相变应变同向，两者叠加后在材料内引入高幅残余应力。

（2）连续冷却过程残余应力的形成包括3个阶段，分别为热应力主导阶段、表面相变主导阶段和心部相变主导阶段。3个阶段之间通过前一阶段的应力对后一阶段相变塑性应变的影响而相互关联，带钢内最终的残余应力由心部相变所产生塑性应变所决定。

（3）相变塑性应变的大小及方向与加载在相变瞬间的应力直接相关。对于NM400而言，在带钢表面相变阶段，相变塑性应变与相变应变方向相反，抑制表面相变阶段残余应力的增长；在带钢心部相变阶段，相变塑性应变与相变应变方向相同，促进心部相变阶段残余应力的增长。

本文摘自《钢铁》2023年第4期