基于MRD-DDPG的机械臂避障路径规划方法*

付子强,郑威强,张立萍,何 丽,袁 亮,邵明明

(1.新疆大学机械工程学院,乌鲁木齐 830047;2.北京化工大学信息科学与技术学院,北京 100029)

0 引言

随着机械臂的应用越来越广泛,机械臂的路径规划成为机器人控制的重要组成部分。但传统的机械臂路径规划方法[1-3]在有障碍物的场景下面临着动态规划较差、智能性较低的问题。而深度强化学习的发展,让智能体具备了自主学习和自主规划的能力[4-6]。

目前,学者们对深度强化学习进行了以下研究。EVERETT等[7]使用混合CPU/GPU的A3C方法,提升了运动规划速度,实现了避障任务的快速运动规划;赵寅甫等[8]提出了机械臂控制模型先2D后3D的训练方法,大幅缩短了训练时间;POPOV等[9]基于DPG算法,融合A3C分布式思想,将训练16台机器人所用的时间成功缩短到10 h,提高了数据收集率;李跃等[10]提出了一种新型方位奖励函数的机械臂轨迹规划方法A-DPPO解决机械臂轨迹规划方法在未知环境中学习效率偏低的问题;JIANG等[11]设计了基于DDPG的机器人操作算法,构造了非对称的AC结构,并在演员网络结构中加入了辅助任务分支,可以有效提高学习效率。除此之外,李龙等[12]提出了一种基于接近视觉传感器的避障路径规划方法,解决了人工势场法的局部最优问题,并在UR10机械臂的小臂连杆验证此方法的有效性;李广创等[13]通过DQN算法离线训练控制机械臂规划出一条无碰撞的路径,具有较强的避障能力;FUJIMOTO等[14]在双Q的基础上提出TD3算法,解决了DDPG算法Q值高估问题,并在OpenAI Gym的平台上验证了TD3算法的性能;ANDRYCHOWICZ等[15]提出HER(hindsight experience replay)算法,并在OpenAI Gym平台中极大的提高了机械臂任务的成功率。

虽然深度强化学习算法发展较为成熟,但在机械臂路径规划应用方面,仍存在学习效率低、样本利用效率低的问题,特别是存在障碍物的工作环境中尤其明显。由此提出了多经验池延迟采样的方法,实现了对样本的有效利用,解决了学习效率低的问题;设计了基于位置的避障奖励函数,解决了机械臂交互探索过程中的奖励稀疏问题;并成功实现了MRD-DDPG算法在障碍物工作环境中的避障路径规划任务。

1 基于多经验池延迟采样的深度确定性策略梯度算法

本文在DDPG算法的基础上通过改进经验池机制,从而提出MRD-DDPG算法。MRD-DDPG算法具有和DDPG算法相同的4个神经网络,MRD-DDPG神经网络模型如图1所示。Actor网络负责策略网络参数θμ的迭代更新,根据当前状态st选择当前动作at,并生成st+1和rt;Actor目标网络负责根据经验回放池中采样的下一状态st+1,选择最优下一动作at+1;Critic网络负责价值网络参数θQ的迭代更新,计算当前Q值;Critic目标网络计算目标Q值。

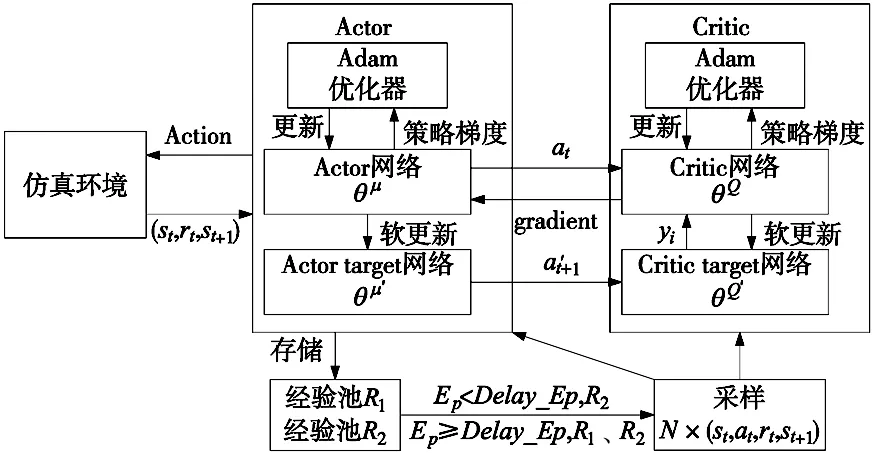
图1 MRD-DDPG神经网络模型

为了减少单一经验池的复杂度增加样本的利用率,根据机械臂与环境交互时是否完成规划任务、是否发生碰撞,将获取的样本分为正样本、普通样本和负样本。其中正样本为完成规划任务的样本、普通样本为既没有完成规划任务又没有发生碰撞的样本、负样本为发生碰撞的样本。

MRD方法则将获取的正样本、普通样本分别存储在2个经验池中,在训练过程中先从普通样本经验池中采样,在延迟固定Episode后再按比例从2个经验池中随机采样。MRD-DDPG算法的流程图如图2所示。

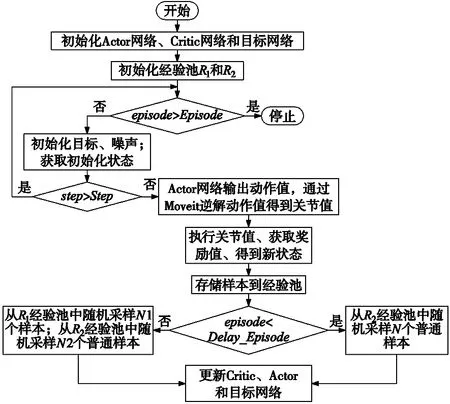
图2 MRD-DDPG算法流程图

2 机械臂环境交互系统

MRD-DDPG算法的每个step与环境进行交互的过程如图3所示。Agent在时间步t从仿真环境观察到的状态st,根据Actor的现有策略π来选择动作at作为机械臂的执行动作,执行动作at到达下一个时间步t+1后,Agent从仿真环境中获取状态st+1、根据奖励函数获取奖励值rt+1,随后按照策略与环境交互直到周期结束。机械臂在训练过程中,并没有通过ROS对真机进行控制,而是在测试过程中,实现仿真与真机的联控。在深度强化学习算法中状态空间、动作空间以及奖励函数起着关键性作用,分别用状态向量描述状态空间的环境特征,动作向量描述动作空间的动作输出,奖励函数来描述交互的奖惩程度。

图3 每个step的环境交互系统

2.1 状态向量

一个好的状态向量可以用来加速Agent学习速度,使算法可以更快的收敛。在实验中与环境相关的变量如图3所示,有机械臂抓取点位置E(机械臂末端下方15 cm处)、机械臂抓取点在XY平面的投影位置E′、障碍物位置O、目标位置G;根据以上变量定义状态向量为:

State=[E′O1,EO1i,E′O2,EO2i,EG,EGi]

(1)

式中:i=x、y、z,E′O1、E′O2为E′点与O点的水平面距离,EG为E点与G点的空间直线距离,EO1i、EO2i、EGi为EO1、EO2、EG空间直线在X、Y、Z三个坐标轴的距离。

2.2 动作向量

深度强化学习算法应用在机械臂上,一般是Actor网络直接输出机械臂关节值q或关节增量Δq来控制机械臂进行正向运动,但是正向运动控制在环境复杂的情况下需要将关节空间映射到笛卡尔空间,Agent难以获取到有效的数据样本。采用Actor网络输出机械臂抓取点三维坐标的逆向运动方法,这个方法根据输出的抓取点坐标进行机械臂逆解得到一组无碰撞的机械臂各关节值,然后通过得到的机械臂关节值控制机械臂。因此定义动作向量为:

Action=[Ex,Ey,Ez]

(2)

式中:Ex、Ey、Ez为抓取点的三维坐标。

2.3 奖励函数的设计

为提高机械臂在有障碍物环境中的路径规划学习效率,利用位置E、位置E′、位置O和位置G设计了一种新型位置奖励函数,如图4所示。在存在障碍物的环境下,机械臂既要躲避障碍物,又要能够到达目标位置。因此针对障碍物设计了对应的避障惩罚函数和碰撞惩罚函数,针对目标物设计了目标奖励函数和终止奖励函数。

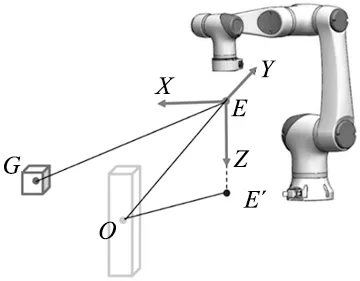
图4 位置奖励函数示意图

(1)避障惩罚函数:避障惩罚函数根据位置E′与位置O水平面之间的距离E′O和正态分布建立,如式(3)所示:

(3)

式中:E′O为机械臂抓取点与障碍物水平面之间的距离,c1为惩罚值阈值,主要来调节惩罚程度;c2、c3为调节系数,主要调节各个惩罚区域惩罚值的收敛速度。

以障碍物为中心,将惩罚区域分为碰撞区、警示区和安全区,如图5所示为惩罚区域和惩罚函数对应图,横坐标为E′O,纵坐标为对应的惩罚值。碰撞区为深灰色区域,区域半径d1为障碍物的最大半径和机械臂末端的半径之和;警示区为浅灰色区域,区域半径d2大小为障碍物的最大半径和机械臂末端的直径之和;安全区为绿色区域外,其大小为机械臂所能达到的最大范围。

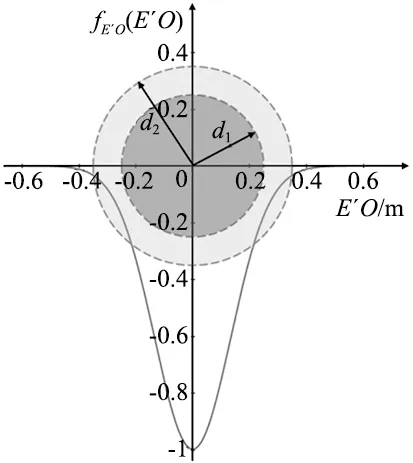
图5 避障惩罚函数区域对应图

(2)目标奖励函数:目标奖励函数根据机械臂抓取位置E与目标物位置G之间的空间距离,采用分层奖励的形式引导机械臂到达目标位置。如式(4)所示为分层奖励函数,以机械臂抓取点与目标物之间的距离进行分层。

(4)

式中:EG为机械臂抓取点与目标物之间的空间距离,ak(k=1,2,3)为奖赏程度,|ak|值越大表征奖赏程度越高;bn(n=1,2,3)用来连接各层,防止层与层之间出现奖励值堆叠的问题。

(3)碰撞惩罚函数:碰撞惩罚函数主要用来约束机械臂与障碍物、工作台之间不要发生碰撞。碰撞惩罚函数如式(5)所示,其中a取-200:

fcollision=a

(5)

(4)终止奖励函数:终止奖励函数主要是用来奖励机械臂到达目标位置,当EG<2 cm,则认为机械臂完成避障路径规划任务。终止奖励函数如式(6)所示,其中b取400:

fdone=b

(6)

故设计出的最终奖励函数如式(7)所示:

R=fEO(EO)+fEG(EG)+fcollision+fdone

(7)

3 机械臂模型及仿真环境

通过将所提出的MRD-DDPG算法应用在Gazebo仿真平台中建立的机械臂模型进行实验验证。其中,机械臂模型以大族机械臂E05型的六自由度协作机械臂为原型。

3.1 机械臂建模

根据大族机械臂的参数建立其D-H坐标系,如图6所示为机械臂的D-H坐标系。

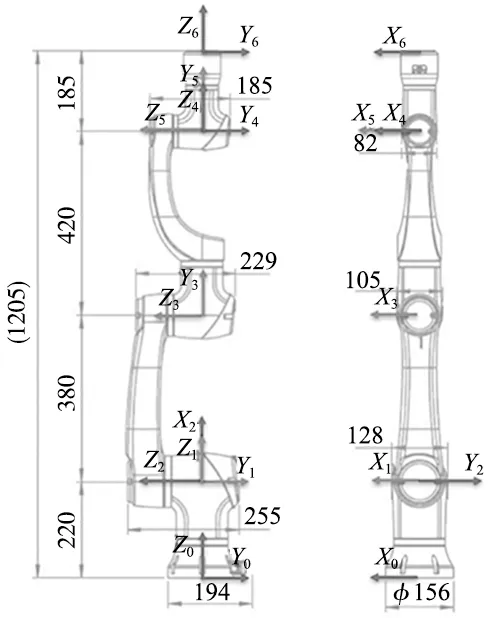
图6 机械臂D-H坐标系

根据机械臂D-H坐标系,列出用于描述各连杆以及相邻连杆之间的4个参数,其中,θi为关节角;αi为机械臂的连杆转角;ai为相邻关节间连杆的长度;di为相邻关节间连杆的偏移量,如表1所示为机械臂D-H参数表。

表1 D-H参数表

3.2 仿真环境搭建

仿真环境主要有大族六自由度协作机械臂的模型、1个试验桌、目标物和多个障碍物。如图7所示为仿真环境1,障碍物有2个大小相同的长方体,其长宽高分别为7 cm、7 cm、30 cm。如图8所示为仿真环境2,障碍物为1个长宽高为5 cm、40 cm、30 cm的长方体;1个长宽高为40 cm、4 cm、20 cm的长方体;1个长宽高为4 cm、50 cm、40 cm的长方体。如图9所示为仿真环境3,障碍物为2个长宽高为7 cm、7 cm、30 cm的长方体;1个长宽高为5 cm、40 cm、30 cm的长方体;1个长宽高为4 cm、50 cm、40 cm的长方体。

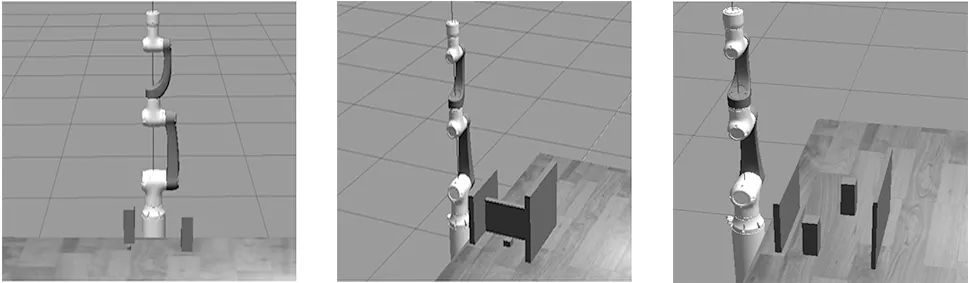
图7 机械臂仿真环境1 图8 机械臂仿真环境2 图9 机械臂仿真环境3

4 实验与分析

本文以机械臂完成路径规划的平均成功率作为算法性能的评判指标。如式(8)为单次实验的成功率的定义。

(8)

式(9)则为平均成功率的定义,即多次实验成功率的平均值,实验的次数N取值为3次。

(9)

4.1 超参数设置

MRD-DDPG算法在实验过程中所使用的超参数如表2所示。

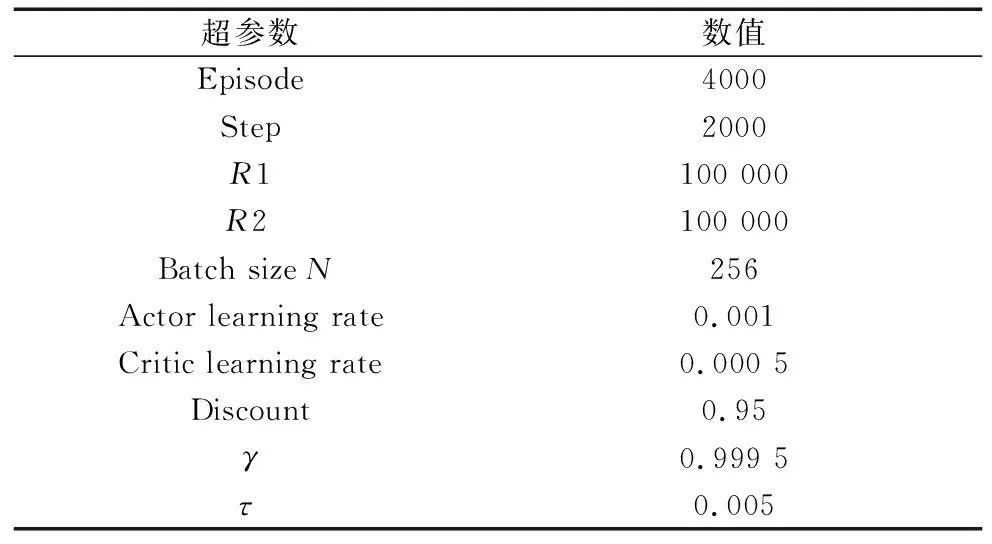
表2 MRD-DDPG算法的超参数

4.2 MRD参数的影响

对提出的MRD方法进行分析,主要探究MRD方法的参数对算法的影响效果。因此针对MRD方法的2个参数,即不同延迟Episode和采样比例,在仿真环境1中进行参数探究的实验。

针对不同延迟Episode的对比实验,设定延迟Episode为400、600、800、1000、1200来进行参数对比。经实验发现,如图10所示,在延迟Episode为600时MRD-DDPG算法训练的效果最好;当延迟400Episode到800Episode时,平均成功率在95%以上,训练效果较好。

在延迟600Episode的MRD-DDPG算法的基础上探究经验池的采样比例对算法性能的影响,实验结果如图11所示。经实验发现正样本与普通样本的采样比例为0.5时效果最好,当采样比例小于0.4或者大于0.7时,训练效果会变差。

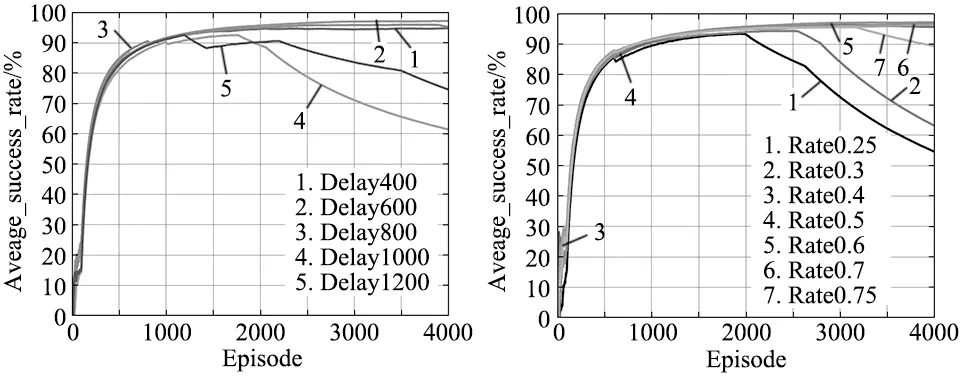
图10 不同延迟Episode下的平均成功率 图11 不同采样比例下的平均成功率

4.3 算法对比与分析

在仿真环境1中进行两组对比实验,一组是MRD与其他种类的经验池进行对比对比分析;另一组是MRD-DDPG与其他同类算法的对比分析。

在第1组实验中,将DDPG算法分别应用单一经验池、多经验池(multi-replay buffer,MR)、非负样本经验池(non-negative sample,NNS)、非负样本多经验池(MR-NNS)以及延迟采样多经验池(MRD),通过对比完成规划任务的平均成功率验证MRD的有效性。如图12所示为MRD和不同经验池的性能对比。通过实验数据可以发现,MR-DDPG和MR-NNS-DDPG的成功率几乎接近于2%,NNS-DDPG和原始的DDPG算法最终的平均成功率在10%左右,MRD-DDPG算法的平均成功率在97%左右。经此可以说明MRD在保证样本一定的比例后,再进行采样能够大幅提升训练效果。

第2组实验将MRD-DDPG算法与DDPG和TD3算法进行对比,同时也测试了MRD在其他算法上是否有效。如图13所示为DDPG、TD3、MRD-DDPG、MRD-TD3的训练结果。由图13可知,MRD-DDPG算法其成功率比DDPG算法提高了88%、比TD3算法提高了91%。并且MRD方法不仅可以提升DDPG算法的性能,同样可以大幅度提高TD3算法的性能,MRD-TD3比TD3算法提高了76%。

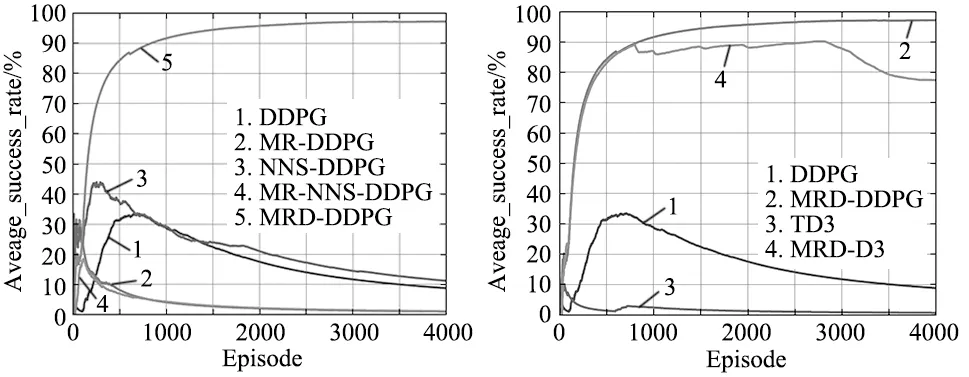
图12 不同经验池下的平均成功率 图13 不同算法下的平均成功率

4.4 MRD-DDPG实验验证与分析

仿真实验分别在仿真环境1、仿真环境2、仿真环境3各测试了40组,测试的采样比例为0.5、延迟Episode为600。

如图14～图16所示为各个仿真环境中测试40组中的一组路径轨迹。经实验发现,MRD-DDPG算法能够很好的规划出一条无碰撞的路径,使抓取点与目标点的误差保持在2 cm以内。

图14 仿真环境1规划路径 图15 仿真环境2规划路径 图16 仿真环境3规划路径

如表3所示为机械臂规划的测试结果,在仿真环境1中规划了40次,成功率为100%,最大规划时间为2.206 s,最小时间为0.255 s,平均时间为0.638 s;在仿真环境2中规划了40次,成功率为100%,最大规划时间为1.923 s,最小时间为0.153 s,平均规划时间为0.706 s;在仿真环境3中规划了40次,成功率为97.5%,最大规划时间为1.761 s,最小时间为0.353 s,平均规划时间为0.712s。表4为其它算法[16-19]完成规划所需时间,由此可知提出的算法可以满足机械臂规划的实时性要求。

表3 MRD-DDPG算法的验证结果

表4 其它算法的规划时间 (s)

5 结论

本文将改进后的MRD-DDPG算法用在大族机械臂上,让机械臂根据当前的状态选择最优动作,使机械臂在躲避障碍物的前提下从抓取点位置顺利到达目标点位置。在ROS下的Gazebo仿真环境中对机械臂进行训练和测试来验证方法的可行性和算法的有效性。结果表明,在MRD-DDPG算法下避障路径规划的成功率达97%左右,能够很好的实现避障路径规划任务;相比于传统的避障路径规划方法,本文提出的方法具有更好的实时规划能力。