阀控缸系统反步法控制及半实物仿真分析*

王志科,梁 全

(沈阳工业大学机械工程学院,沈阳 110870)

0 引言

当前,由于阀控缸系统存在高度非线性特性、参数不确定和负载干扰等特点,传统的PID控制器不能很好的实现对系统的运动轨迹有效跟踪控制,因此研究阀控缸系统的非线性有效控制具有重要意义。

在研究者解决非线性问题的众多方法中,反步控制方法做为常用的一种非线性控制器、具有严格标准的数学推导过程并且能够有效抑制被控系统中的负载干扰,其在各领域获得应用。石胜利等[1]针对电液伺服系统具有外负载干扰和输入饱和等问题,提出一种带跟踪微分器和干扰观测器的反步控制算法,减小了反步算法的设计复杂性,同时改善了系统受外部干扰的影响。王海燕[2]提出一种基于反步法和滑膜的复合控制算法,解决了电液伺服系统在采用滑膜算法时系统抖动等问题。GUO等[3]针对非线性单杆液压执行器,设计了一种带全状态观测器的非线性反步控制器,分析了观测器的收敛性。AHN等[4]为改善电液作动器系统位置控制中存在的非线性和不确定特征,采用一种基于改进的反步法和自适应法的复合算法。

然而,目前阀控缸系统算法研究主要依靠纯数学仿真,这种方法使用是虚拟的被控对象和虚拟的控制器,具有成本低、易于实现和对环境要求低等优点,但纯数学仿真的可信度极大的依赖模型的准确度。半实物仿真中有虚拟的被控对象和真实的控制器,因有实物参与仿真,故可靠性高且能在极端条件下对控制器进行实际测试,极大的提高了控制器中控制算法的设计效率。因此,半实物仿真技术在仿真控制算法验证、被控对象数学模型检验和系统硬件评估等方面起着不可替代的作用[5]。韩桂华等[6]因电液力伺服系统不能较为准确的建立出精确的数学仿真模型而辨识模型,利用xPC实时半实物仿真技术进行模型辨识试验且证明了该辨识模型的可行性。同时在半实物仿真下证明了复合模糊PID算法比PID、模糊控制器的控制精度高。罗亮[7]针对注塑机料筒温度控制算法设计中安全性差和开发时间过长原因,依靠NI RIO9623控制器和LabVIEW编程建模等技术设计了半实物仿真系统,通过仿真测试验证了该仿真系统的正确性。李超等[8]利用基于XPC的半实物仿真技术验证模糊滑模控制算法对导弹电液伺服机构控制,从仿真试验结果可以看出喷管的实际角度与期望角度基本一致,控制精度满足系统要求,并且证明该控制算法的有效性。LINJAMA[9]利用硬件在环半实物仿真技术测试控制器,验证了系统虚拟的仿真模型可以代替实际液压系统。

综上所述,在考虑外负载干扰和系统非线性特征等影响因素下,本文依据半实物仿真系统为研究工具,提出非线性反步法控制研究阀控缸位置控制精度问题。考虑到半实物仿真平台的经济性、开发难度和通用性等因素,设计一种基于研华数据采集卡和Linux实时操作系统相结合的半实物仿真系统,本阀控缸半实物仿真系统具有快速修改控制算法及参数、易于操作和成本低等特点。

1 阀控缸系统数学模型

本文选用阀控对称缸作为仿真对象,其仿真模型包括电液伺服阀孔口流量方程、液压对称缸流量和力平衡方程方程、电液伺服阀动态特性方程。阀控缸系统的动态运动轨迹控制主要由液压伺服阀完成,伺服阀根据输入信号改变液体输出流量进而控制液压执行机构的运动。阀控缸系统动力机构图如图1所示。

图1 阀控缸动力机构图

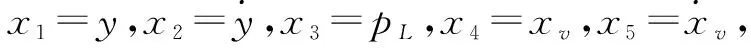
(1)

根据文献[10],sgn(·)代表一种符号函数。

(2)

2 反步控制算法设计

反步法广泛用于非线性系统的控制研究中,特别适合对非线性阀控缸系统的位置控制。该算法核心思想将复杂的被控系统转化成与系统阶数相同的子系统,后根据李雅普诺夫稳定性理论逐步推导求解出虚拟控制器,确保系统具有较强的稳定性,从而对系统进行有效跟踪控制[11-12]。为了便于反步算法的推导,忽略系统内外泄漏的影响。

设ei=xi-xi,d,i=1,2,3,4,5。其中x1为液压缸实际运动位移,x1,d为液压缸期望位移,e1为液压缸期望位移与实际运动位移两者误差。

反步法第1步:令i=1,则e1=x1-x1,d,对e1求导:

(3)

(4)

对V1求导,可得:

(5)

第2步:令i=2,则e2=x2-x2,d,对e2求导:

(6)

(7)

对V2求导,可得:

(8)

第3步:令i=3,则e3=x3-x3,d,对e3求导:

(9)

(10)

对V3求导,可得:

(11)

第4步:令i=4,则e4=x4-x4,d,对e4求导:

(12)

(13)

对V4求导得:

(14)

第5步:令i=5,则e5=x5-x5,d,对e5求导:

(15)

(16)

对V5求导得:

(17)

当上述k1、k2、k3、k4和k5都选取正数时,则李雅普诺夫函数V1、V2、V3、V4和V5都正定,各自导数都负定,此时系统稳定,反步算法推导完成。

3 半实物仿真系统搭建

半实物仿真就是在仿真过程中,将真实硬件设备(实物控制器)和仿真计算机搭建的被控对象仿真数学模型连接起来,相互配合进行试验的技术[13]。

3.1 半实物仿真平台框架

阀控缸半实物仿真平台主要由仿真控制计算机与研华USB-4704板卡等硬件组成,半实物仿真平台框架如图2所示。其中非实物部分为虚拟的阀控对称缸系统模型,实物为研华USB-4704控制板卡。

4.2.1 在园林景观设计中要注意色彩主次搭配，遵循统一性原则。每一处园林景观都有自己的风格特色，设计中都有园林自己的主要的整体色彩，其它辅色选什么，以及怎样使主色和辅色统一，都是要认真思考的问题。统一性原则是指在园林景观设计中，园林环境的整体色调要和园林的整体风格、形式联系在一起，园林景观的整体配色，必须要统一，不能给人以突兀的感觉。园林景观设计中优先考虑大面积主色调的存在，围绕该色彩进行辅色变化，明暗对比，冷暖对比，面积大小对比，主色辅色相辅相成，在统一中追求变化，在变化中创造统一。

图2 阀控缸半实物仿真平台框架

仿真控制计算机主要完成阀控缸系统仿真模型搭建、液压缸运动轨迹的实时显示、仿真参数及控制模型的在线修改和实时运行仿真模型,该仿真机选用个人PC机。

研华USB-4704板卡在阀控缸半实物仿真平台中充当实物控制器及数据采集的角色,主要完成阀控缸系统中液压缸的位移、速度和负载压力以及阀芯位移和速度等模拟量的采集,同时根据设计的控制算法进行运算和比较,输出控制信号给仿真控制计算机。

3.2 半实物仿真平台软硬件分析

阀控缸半实物仿真平台软件主要包括Visual Studio code、AMESim仿真软件和GNU Scientific Library(GSL)科学计算库。

Visual Studio code负责搭建虚拟的阀控对称缸仿真模型。GSL算法库求解效率高、开源免费[14]。通过Visual Studio code调用GSL算法库求解系统仿真模型。AMESim承担两方面作用:在线显示液压缸运动轨迹过程和参数;进行半实物仿真系统测试验证。

研华USB-4704板卡通过二次开发使其满足半实物仿真试验时实时数据的采集、处理以及控制信号的生成、输出。由于有真实的硬件参与到半实物仿真过程中,这样需要仿真系统具备实时性[15]。因此半实物仿真需要使用实时操作系统,本文采用Linux操作系统加Preempt-RT内核补丁实时运行仿真模型的解算数据,完成与实物研华板卡在线数据采集和交换。

4 仿真结果分析

选用阀控缸PID控制进行AMESim纯数学仿真和半实物仿真以验证搭建的阀控缸半实物仿真系统的正确性,纯数学仿真模型如图3所示。阀控缸系统的仿真具体参数如表1所示。

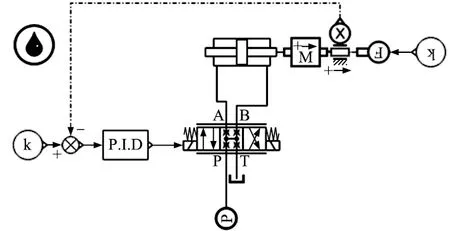
图3 纯数学仿真模型

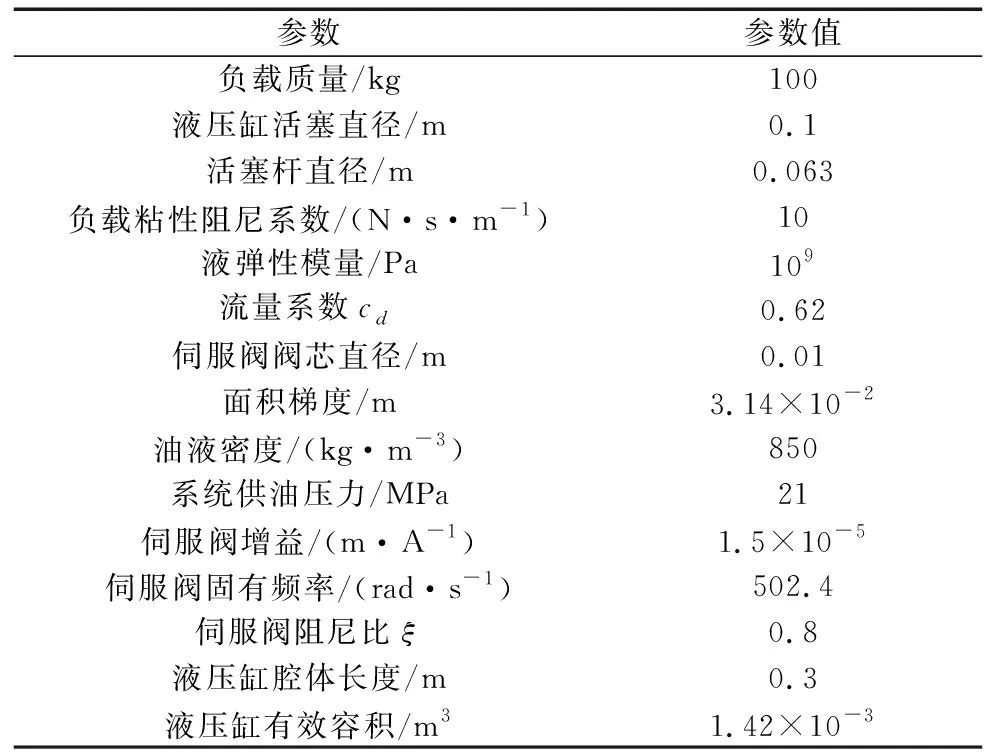
表1 阀控缸系统参数

4.1 半实物仿真系统验证

在相同的PID控制算法参数下,即P=500,I=300,D=15,输入信号为阶跃信号u=0.01 m,仿真时长设定5 s,纯数学仿真和半实物仿真结果如图4所示。

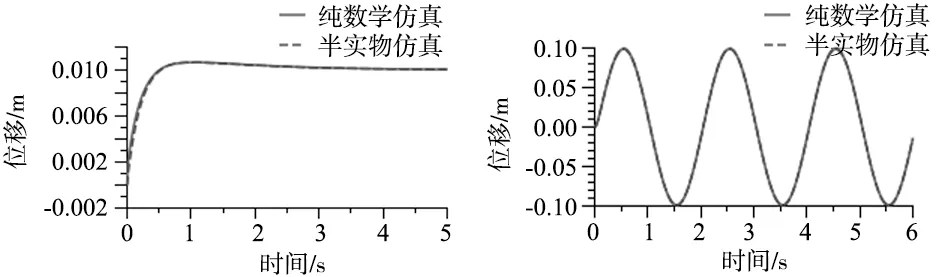
图4 阶跃信号下纯数学仿真与半实物仿真结果 图5 正弦信号下纯数学仿真与半实物仿真结果

由图4可以看出,尽管半实物仿真和纯数学仿真的结果不完全一致,考虑到半实物仿真过程中有实际硬件设备参与仿真,两者在1 s时超调量相同和4 s后两者都趋于平衡,图像变化趋势完全一致。

当输入信号为正弦信号x=0.1sin(πt)时,在相同PID控制算法参数下,即P=2000,I=50,D=10,仿真时长设定6 s,纯数学仿真和半实物仿真结果如图5所示。从仿真曲线可以看出,两者曲线基本完全相同。

通过图4～图5可得,当改变系统输入信号类型和PID仿真参数等条件,本文搭建的阀控缸半实物仿真系统和AMESim纯数学仿真软件的仿真结果基本一致,证明该阀控缸半实物仿真系统的正确性,为后续反步控制器的调试验证奠定了基础。

4.2 反步法仿真分析

当阀控缸系统在负载干扰情况下,在阀控缸半实物仿真系统上通过阶跃信号和两种振幅和频率的正弦信号做为期望信号,以评估本文设计的反步法控制精度和抗干扰能力。

选定幅值为0.02 m的阶跃信号为期望位移,仿真时长为2 s。为模拟系统实际运行过程中受到的负载干扰,设定在0 s时输入2000 N的阶跃力干扰。经过多次调试控制算法参数,选定PID控制算法参数P=800,I=0.5,D=0.01,反步算法参数k1=20,k2=300,k3=400,k4=400,k5=500,两种算法控制效果如图6所示。

图6 阶跃信号下PID和反步控制器半实物仿真结果 图7 正弦信号下PID和反步控制器半实物仿真结果

在负载力干扰时,反步法控制和PID控制算法都有较好控制精度和稳定性,反步法控制下系统达到稳定的时间为0.192 s,而PID控制下系统达到稳定时间为0.619 s,可见反步算法下阀控缸系统动态响应时间更快,能迅速完成系统运动轨迹的跟踪控制。

当采用频率为1 Hz、振幅为0.01 m的正弦信号,即x=0.01sin(2πt)时,反步算法参数k1=60,k2=500,k3=300,k4=300,k5=800,PID控制算法参数P=5000,I=5,D=0.5,仿真时长为5 s。在0 s时输入2000sin(2πt)+1000t时变负载力干扰,两种算法控制效果如图7～图9所示。在施加干扰后, PID控制时,液压缸位置跟踪误差较大,最大误差为1.3 mm;当使用反步控制算法时,液压缸位置跟踪误差最大为0.85 mm,最大误差相较于期望位移幅值减小了4.5%,运动轨迹跟踪精度和稳定性优与PID控制。

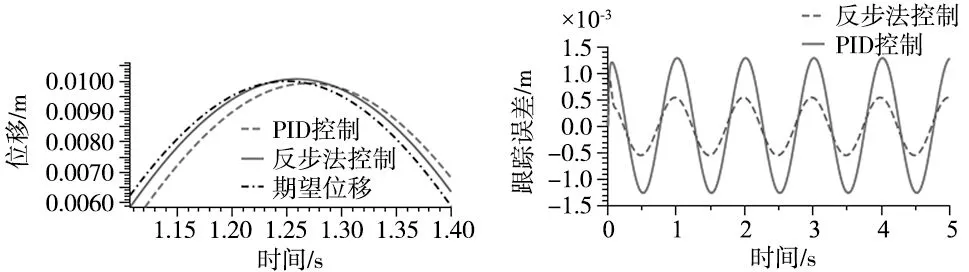
图8 1.11～1.40 s局部放大图 图9 正弦信号液压缸运动轨迹误差图

当采用频率为0.5 Hz、振幅为0.1 m的正弦信号,即x=0.1sin(πt)为系统的期望信号,在0 s时输入5000sin(πt)+1000t时变负载力干扰,反步算法参数k1=90,k2=500,k3=500,k4=500,k5=800,PID控制算法参数P=10 000,I=500,D=10,设定仿真时长为8 s。两种控制方法下液压缸的实际运动轨迹响应曲线如图10～图12所示。在施加干扰后,当使用反步控制算法时,运动轨迹跟踪精度高,液压缸位置跟踪误差最大为2.6 mm;而PID控制器的跟踪精度和抗干扰能力较差,液压缸位置跟踪系统最大误差为3.2 mm。

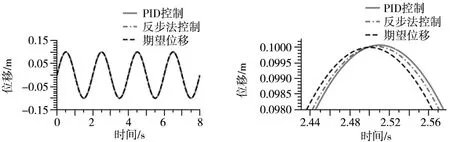
图10 正弦信号下PID和反步控制器半实物仿真结果 图11 2.43～2.57 s局部放大图

图12 正弦信号液压缸运动轨迹误差图

由此可得,在半实物仿真环境下,当阀控缸系统受到负载扰动时,相比于传统PID控制器,本文提出的反步控制器在两种不同振幅、频率的正弦和阶跃输入信号下都能迅速稳定实现系统稳态响应,改善液压缸运动轨迹和具有较强的抗干扰能力。

5 结束语

(1)建立了阀控对称缸系统数学模型,针对阀控缸的非线性特点以及系统存在的负载干扰,提出了非线性反步控制算法。为研究和调试该算法,利用研华板卡和Linux操作系统搭建了阀控缸半实物仿真系统,并验证半实物仿真系统的正确性。

(2)在施加负载干扰时,通过阀控缸半实物仿真系统完成了反步控制算法和PID算法对液压缸的运动轨迹的跟踪试验,两种控制算法都能实现稳态控制,而PID控制算法虽设计方便,但因基于输出反馈以及比例、积分、微分3个参数相互影响,取得的控制效果较差。反步法根据准确仿真数学模型进行严格的数学推导计算,较PID算法具有参数调试方便、响应速度快、很高的抗扰能力,为设计非线性阀控缸位置控制系统提供一些参考价值。