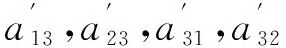基于定速比的三感应电机多频复合同步控制*
2023-08-02王国辉
潘 成,贾 磊,王国辉
(沈阳理工大学机械工程学院,沈阳 110159)
0 引言
多轴运动在工程中有着广泛的应用,如振动筛、机器人、螺旋桨飞机、多轴数控机床和振动给料机[1-4],然而,传统行业中的大多数多轴运动通常是用皮带、齿轮、链条等来操作的,这些多轴运动可以归类为强迫同步运动。根据可靠性理论,系统的总可靠性指标是各部分可靠性指标的乘积。因此,增加现有的部件,降低可靠性指标。轴与轴之间采用齿轮、皮带或链条连接,不仅降低了系统的可靠性指标,而且增加了成本。
基于上述现象,首次提出了两个偏心电机的自同步理论来代替Blekhman的强迫同步[5-6]。WEN等[7]利用自同步理论研究了一个振动系统中两个偏心电机的问题,并给出了同步条件和同步状态的稳定性判据。JUNKI[8]则在此基础上实现了二次频率同步和三次频率同步。但是无论采用哪种方法,都不能在一个动力学模型中实现任意性的多频自同步运动。随着机电工程的发展,ZHAO等[9]建立了机电耦合模型来解决一个振动系统中两个偏心电机的自同步问题。然而具有3个偏心电机的自同步理论并不适用于工程。针对这一现象,提出了控制同步理论来解决这一问题。许多研究人员已经用各种控制方法实现了同步运动[10-13]。但是,目前还没有提出控制相位差的方法。KONG等[14-16]完成了一个振动系统中多个偏心电机的零相位差控制同步。JIA等[17]实现了一个振动系统中两个偏心电机的多频控制同步。控制同步虽然实用于工程,但与自同步相比增加了投资,因此为了减低成本和简化机械结构,复合同步运动理论被提出。KONG等[18-19]研究了相同频率情况下的复合同步理论。
根据以上叙述自同步和控制同步都已经得到了有效研究,但是复合同步目前只有同频率的研究,而对多频部分的研究并不多见。工程实际中多频复合同步理论在振动筛、振动给料机等方面研究也未有所涉及。本文对基于定速比的3台感应电机多频复合同步控制进行了研究,采用多频复合同步的方法,使得振动系统可以根据不同的频率实现不同的响应。不仅解决了同频振动筛的堵筛现象,而且放大了幅值提高了工程上的有效性。并对所提出的多频复合同步方法进行了数值仿真和分析,验证了该方法可以实现任意定速比的多频复合同步控制。
1 三机驱动振动系统动力学模型
1.1 三机驱动机械系统的动力学模型
振动系统中3个感应电机的多频复合同步的动力学模型如图1所示。振动系统自下而上安装,一个钢制支架固定在地面上,在钢支架上安装了4个弹簧,在x、y和ψ方向上分别提供振动系统的阻尼和刚度。弹簧的减振是粘性减振,不能单独考虑,它们被视为3个方向上的总等效阻尼项。由于弹簧的振动,阻尼引起能量耗散,感应电机的参数和振动系统的参数分别如表1和表2所示。弹簧上连接着1个刚体,由3个感应电机驱动分别作为激励器,以水平分布的方式固定在刚体上。如图1所示,电机2位于中线,电机1和电机3沿中心线对称安装,电机3在左边,电机1在右边,电机2逆时针方向旋转,电机1和电机3都沿顺时针方向旋转。根据拉格朗日方程,多频复合同步的动力学方程如式(1)所示:
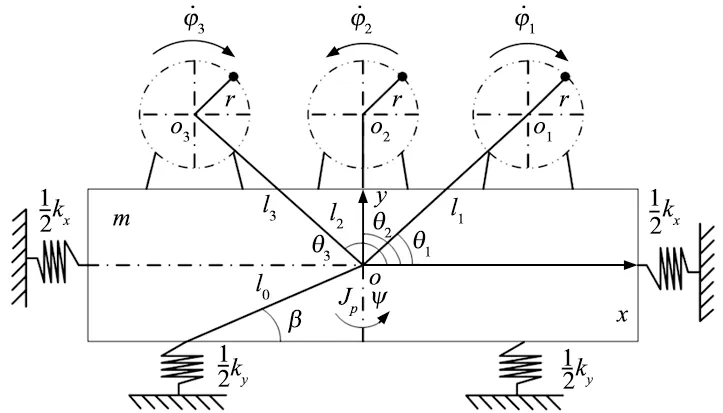
图1 振动系统动力学模型
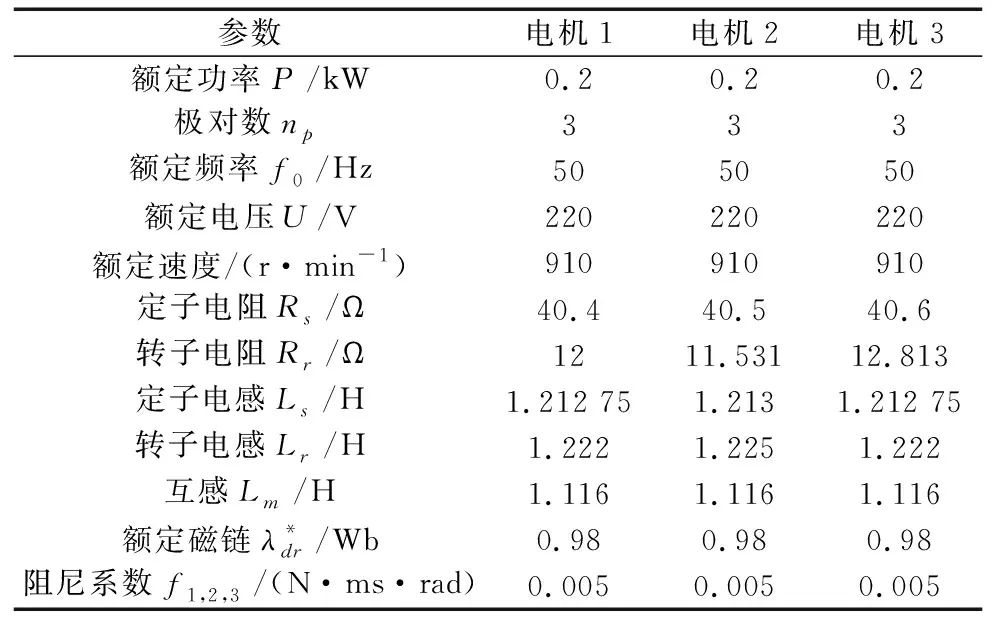
表1 3个感应电机的参数
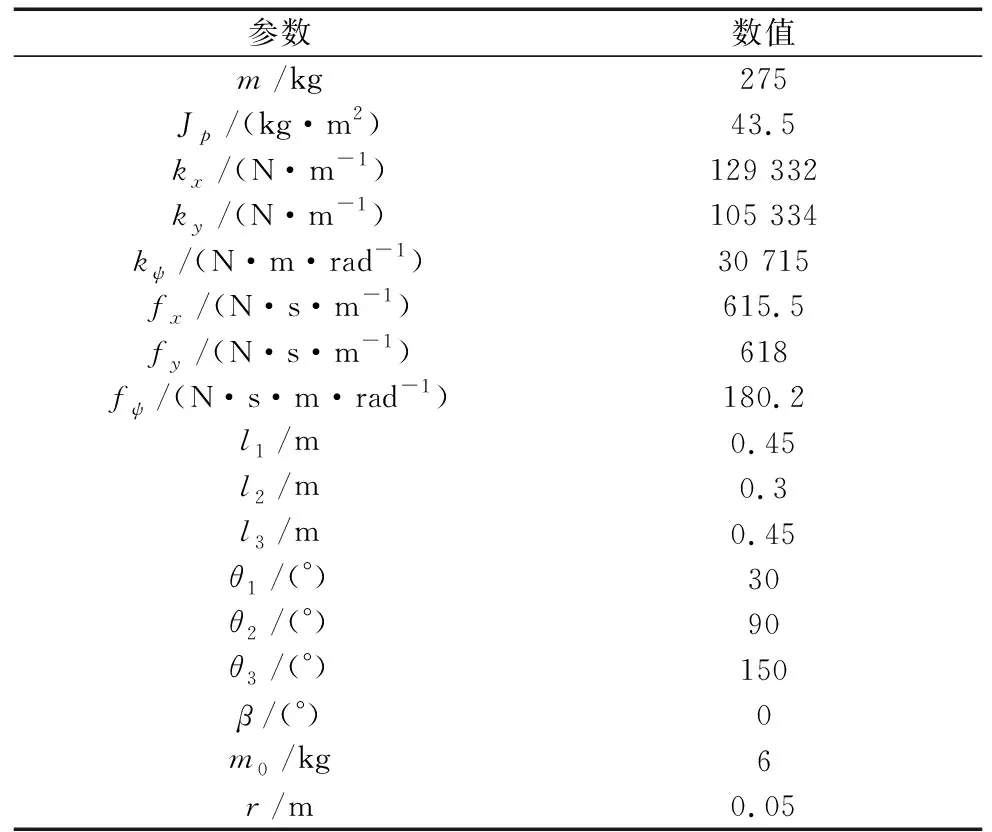
表2 振动系统的参数
(1)
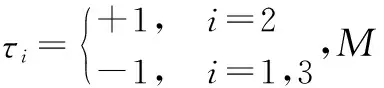
(2)
图中,Jp为刚体的转动惯量,kx、ky为振动系统在x、y方向上的阻尼系数,r为3台电机的偏心半径,l1、l2、l3为机体中心与电机旋转中心之间的距离,θ为同步电动角,φ1、φ2、φ3为3个电机的相位。
1.2 机电系统模型
本文除了考虑动力学模型外,还应该考虑振动系统中感应电机的模型。根据电机理论[9,20],给出了感应电机的模型为:
式(3)、式(4)分别表示感应电机在坐标轴d轴和q轴同步坐标系中的磁链方程和电压方程。由于鼠笼式电机的特点,其内部结构形成短路现象,所以urd=urq。当系统处于稳态时,转子磁链q轴上的分量φrq=0,所以转子磁链的d轴分量φrd就等于转子磁链φr,转子磁链φr是给定值,故转子磁链在d轴上的分量φrd是一个常数,所以φrd等于常数,φrq=0。将式(3)代入式(4),即可表示为式(5)。
(3)
(4)
(5)
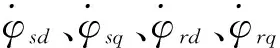
根据感应电机的模型,可以得到以下表达式:
Te=npLm(isqφrd-isdφrq)/Lr
(6)
由于φrd等于常数,并且φrq=0,代入式(6)中:
Te=npLmisqφrd/Lr
(7)
式中:np、Lm和Lr是常量,因此式(7)是关于变量isq的函数。
1.3 多频复合同步响应分析
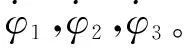
(8)
(9)
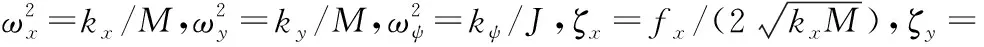
将式(8)代入式(1),忽略高阶项。x、y和ψ方向的响应表示为式(9)。
(10)
平均电磁转矩可表示为:
平均负载转矩可表示为:
(11)
式中:aij,bij和κi(i=1,2,3和j=1,2,3)表达式均在文献[22]中可见。由于电机1和2之间的耦合,φ1-φ2=2α和α=α0+ε4。将相位角展开为泰勒公式,忽略高阶项,代入式(10)可得:
(12)
当振动系统处于稳态时,同步系统的条件是υ=0,式(12)转化为式(13):
(13)
显然矩阵A的行列式不等于0,所以矩阵A是可逆的,令D=A-1B,式(13)可被表示为:
(14)
根据|λI-D|=0,可以得到特征值方程如下:
λ4+d1λ3+d2λ2+d3λ+d4=0
(15)
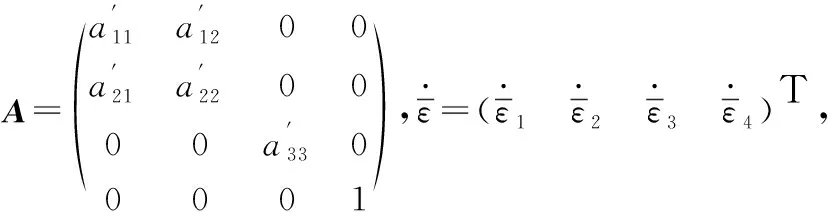
2 控制系统的设计
为实现控制系统的任意性,令p/q=n,以比值n为目标变量,采用模糊PID方法实现多频控制同步。因此,在这一部分,首先提出了一种改进的主从式控制策略。在此基础上,给出了模糊PID控制方法。
2.1 机电耦合系统设计
如图2所示,电机1被认为是主电机,而电机3被认为是从电机。电机3以定速比参数n来跟踪电机1。在电磁系统中引入了转子磁链定向控制(RFOC)及其控制方法。ωt作为初始速度被传递到电机1。通过该控制方法,得到了电机1的转速ω1。显然ω1有两种用途。一种是作为反馈值,以初始转速ωt控制电机1的转速,另一种是获得ω3。最后,电机3的速度ω3作为反馈给从属电机。
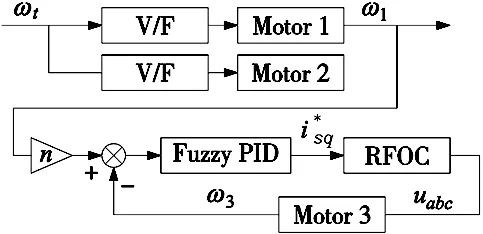
图2 控制系统流程图
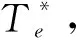
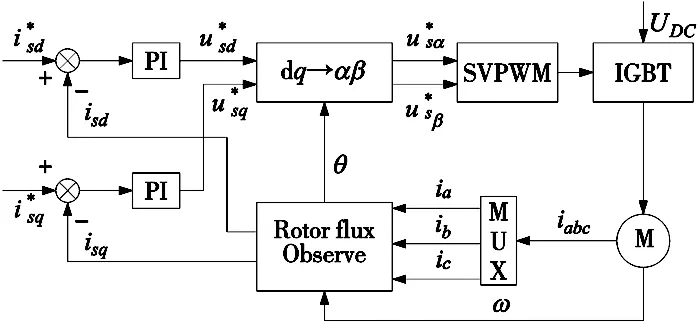
图3 RFOC:转子磁链定向矢量控制
(16)

2.2 模糊PID控制方法设计
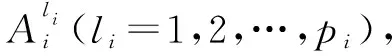
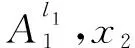
其中,li=1,2(i=1,2),引入乘积推理器,单点模糊器和中心平均模糊器来获取系统的输出变量,这些变量可以表示为:
(17)
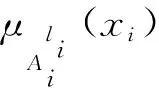
(18)
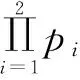
(19)
该方法采用2个输入变量和3个输出变量。输入变量分别为误差(e)和误差变化(ec)。输出变量分别为kp、ki和kd。变量服从两种子函数模型的分布。一种是模型Z(zmf),另一种是三角形模型(trimf)。每个变量都有7种形式。它们分别是NB、NM、NS、Z、PS、PM和PB。其中,“N”表示负,“P”表示正,“M”表示中,“B”表示大,“S”表示小,“Z”表示零。输入值根据规则在图4中选择不同的路径,从而得到不同的输出值。变量如图4所示。
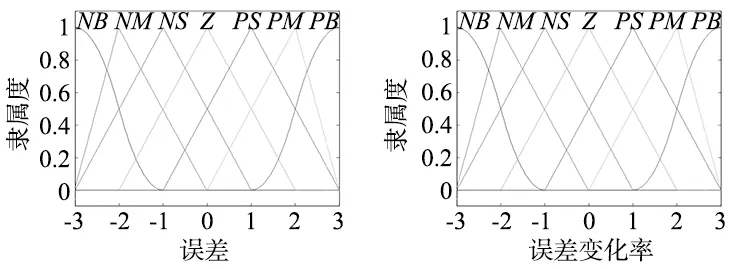
(a) 误差 (b) 误差变化
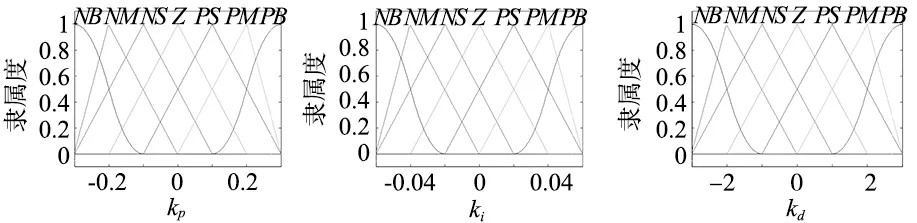
(c) kp (d) ki (e) kd图4 隶属度函数
根据上述模糊规则,引入49个规则以得到式(20)~式(22)。
(20)
(21)
(22)

(a) kp (b) ki (c) kd图5 kp,ki和kd的图形模型
3 仿真分析
此节利用Simulink对多频复合同步进行了可行性分析。首先说明了自同步运动不能用图1所示的动力学模型来实现,然后结合多频控制同步,实现振动系统的多频复合同步运动,此外,还研究了多频控制同步的任意性,验证了所提出的复合同步方法的有效性和可行性。
3.1 多频自同步仿真分析
通过利用图1中的动力学模型研究了自同步运动。如图6a所示,每台变流器采用恒压频比(V/F)的方法将3台电机的频率分别设定为30、30和45 Hz。电机1、电机2的频率均为30 Hz,电机3的频率为45 Hz。图6b表示电机1和电机2之间的相位差。图6c表示电机1和电机3之间,以及电机2和电机3之间的相位差。根据自同步理论,当1.5φ1-φ3=constant时,振动系统可以达到同步状态。然而,它们分别是两条单调递增曲线。通过图6b和图6c,可以知道振动系统不能实现多频自同步运动。图6d~图6f分别是x、y和ψ方向上的响应。由于电机1和电机2之间的相反运动,x方向上的响应幅度在图6e中被稀释。然而,两个电机的力是沿y方向叠加的,因此y方向的响应幅度呈现叠加形式。
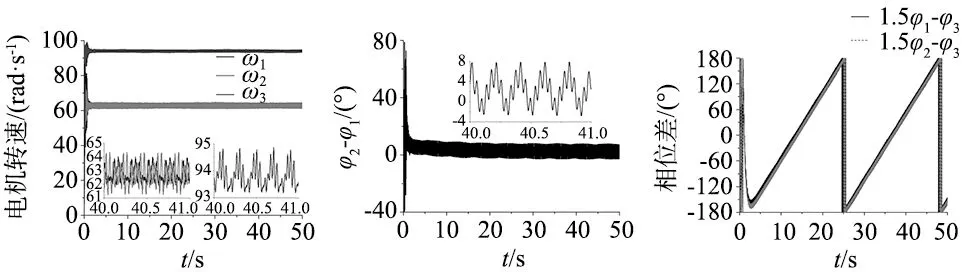
(a) 三台电机速度 (b) 1-2电机相位差 (c) 1-3、2-3电机相位差

(d) x方向响应 (e) y方向响应 (f) ψ方向响应图6 α0=0,n=1.5条件下三感应电机多频自同步
3.2 多频复合同步仿真分析
根据上节的结论,振动系统不能实现多频自同步运动。为了实现这一目标,引入了模糊PID控制方法来解决这一问题。如图7所示,电机1和电机2构成自同步部分。它们的频率都设置为30 Hz。在n=1.5的情况下,电机1和电机3组成多频控制同步部分。图7a显示3台电机的速度。图7b表示3个感应电机的负载扭矩,其值在-2和2之间。根据文献[18],图7b中的3个负载扭矩值满足动力学方程,所以3个感应电机可以正常运行。图7c和图7d分别是电机1和电机2与电机3之间的相位差。图7c表示在中心点0°附近,相位差从-3°到3°的范围波动。这一结果证明了电机1、电机2能够实现自同步运动。从图7d中知,实现了动力学方程1.5φ1-φ3=constant。由此可知,通过这种控制方法电机1、电机3可以实现多频控制同步运动。与图6中的振动系统相比,图7中的振动系统实现了多频复合同步。这是因为当电机1和电机3实现多频控制同步运动时,来自电机3的转矩随着电机1的变化是稳定的,而不是自同步运动中的不规则变化。因此,在图6中的相位差从-4°到8°被调整到图7中的-3°到3°,并且最后电机1和电机2实现了自同步运动,从而振动系统的多频复合同步被实现。图7e~图7g分别是x、y和ψ方向上的响应。由于电机1和电机2在相反方向上的自同步运动,电机1和电机2在x方向上的力被抵消。因此,x方向的响应取决于电机3。这就是图7e呈现基频同步趋势的原因。图7f呈现与3个感应电机在相同方向上旋转的情况相同的现象,因为没有任何影响在y方向上。图7g是振动系统的摆动角度,给出了n=1.5的情形。
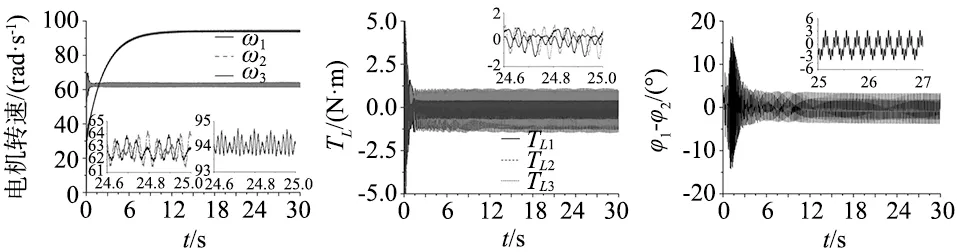
(a) 三台电机速度 (b) 三台电机负载扭矩 (c) 电机1与电机2相位差
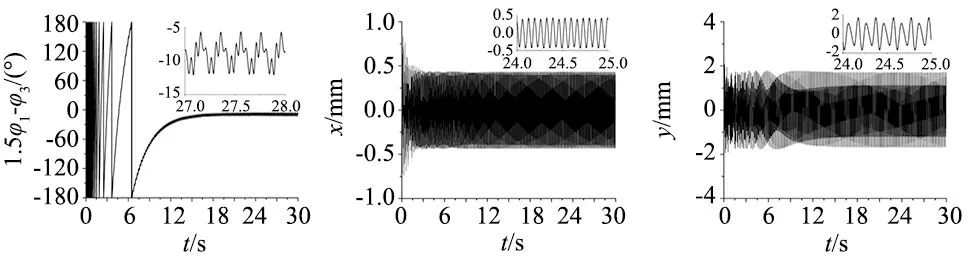
(d) 电机1与电机3相位差 (e) x方向响应 (f) y方向响应
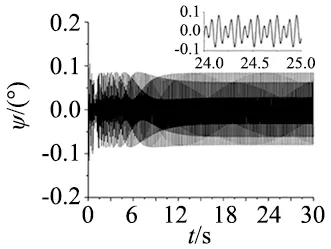
(g) ψ方向响应图7 α0=0,n=1.5,η=50%条件下三感应电机复合同步
为了证明参数n的任意性,将其从1.5调整为1.2。如图8所示,图8b中从-1到1的扭矩载荷也满足动力学方程。图8c表示电机1和电机2之间的相位差。波动范围从-5°到5°。这是由于具有整数和半整数周期的振动系统的稳定性高于非整数周期振动系统的稳定性。文献[17]证明了这一结论。因此,自同步运动部分是稳定的。图8d是电机1和电机3之间的相位差。就像图7d一样,动力学方程1.2φ1-φ3=constant也被实现。所以,改变参数n对实现多频复合同步运动没有影响。图8e~图8g分别是x,y和ψ方向的响应。因此,这一结果证明了参数n的任意性。
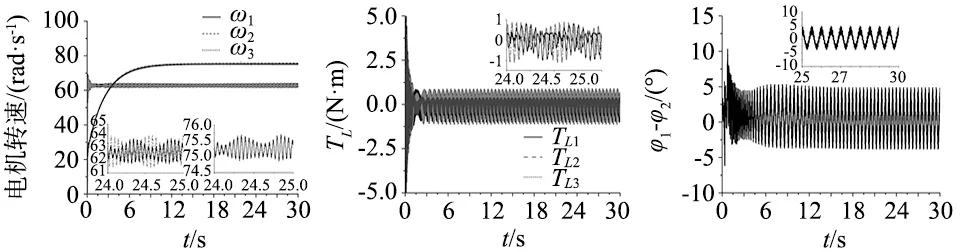
(a) 三台电机速度 (b) 扭矩负载 (c) 电机1与电机2相位差

(d) 电机1与电机3相位差 (e) x方向响应 (f) y方向响应

(g) ψ方向响应图8 α0=0,n=1.2,η=50%条件下三感应电机复合同步
4 结论