永磁同步电动机基于滑模与自抗扰控制研究*

齐 歌,黄文豪,马 丁

(1.郑州大学电气与信息工程学院,郑州 450001;2.河南工业大学人工智能与大数据学院,郑州 450001)

0 引言

永磁同步电动机(permanent magnet synchronous motor,PMSM)由于其功率密度高、可靠性高、输出转矩大等诸多优点,在各个工业领域得到了广泛的应用[1-2]。随着控制理论的快速发展和诸多学者的不断研究,许多的控制策略被应用到PMSM控制系统中,如:模糊控制[3]、模型预测控制[4]、自抗扰控制[5]、自适应控制[6]等,其中滑模控制(SMC)系统因对参数和扰动不敏感,滑动模态的可设计性等优点而被应用于许多领域[7]。传统滑模控制由于切换函数高频转换,容易造成控制信号的抖动,因此设计新型的趋近律抑制系统抖振是诸多学者研究的热点。如岳聪聪等[8]提出一种多幂次趋近律,使系统在不同趋近阶段获得不同的趋近速度,有效减小系统抖振和稳态误差。ASHOK等[9]使用可变开关函数,消除了由恒定开关函数带来的抖振,并通过新型趋近律减少了收敛时间。张国山等[10]提出一种离散滑模变速趋近律,在幂次趋近律基础上引入改进的变指数趋近律和正切函数,加快了收敛速度。JUNEJO等[11]提出一种自适应终端滑模趋近律,有效减少了系统控制输入中的抖振。参考以上文献,可知合适的趋近律可以削弱抖振,提高收敛速度。

为了获得更好的动态性能,本文采用自抗扰控制作用于交轴电流环。针对传统自抗扰控制中fal函数拐点处不平滑而引起的系统抖振、误差较大等问题,选择合适的fal函数能够提高控制器的收敛速度和抗干扰能力,如闫桂林等[12]使用线性函数和正切函数的拟合代替fal函数的指数形式,避免了拐点和较大的误差增益。孙斌等[13]采用fhan函数应用在NLSEF和TD上,实现了误差快速收敛且消除了高频抖振。蒲明等[14]提出一种具有固定时间收敛能力的fal函数,此函数收敛时间较快,且收敛时间上界与初始误差无关,提升了收敛速度和跟踪误差。本文在此基础上对新型fal函数进一步改进,并引入到交轴电流环中。

综上所述,本文提出一种改进趋近律的新型滑模控制方法,作用于永磁同步电动机的矢量控制转速环;并提出一种改进fal函数的自抗扰控制方法作用于交轴电流环。通过Simulink搭建电机控制模型,并与传统滑模控制、自抗扰控制进行比较分析。

1 PMSM数学模型

永磁同步电动机是一个非线性、高耦合系统,电磁关系十分复杂,建立精确的数学模型比较困难。为了简化分析过程,在不影响控制性能的前提下忽略一些影响较小的参数,假设:

(1)空间磁场呈正弦分布;

(2)忽略定子铁心饱和,认为磁路线性,电感参数不变;

(3)不计磁滞和涡流损耗的影响;

(4)转子上无阻尼绕组。

通常采用id=0的永磁同步电动机转子磁场控制,转矩的大小只与定子电流幅值成正比,实现了永磁同步电动机的解耦控制。则永磁同步电机在d-q轴下的定子电压方程为:

(1)

式中:ud、uq为d、q轴电压,id、iq为d、q轴电流,ωe为转子的电角速度。

定子磁链方程为:

(2)

(3)

式中:Ld、Lq分别为d、q轴的电感,在表贴式PMSM中一般认为Ld=Lq;R为定子电枢绕组电阻,ψf为永磁体磁链。

2 速度环滑模控制器设计

滑模控制是一种系统结构随时间不断变化的控制,包括趋近运动和滑模运动两个过程,其中趋近运动的轨迹与趋近律息息相关,不同的趋近律对应趋近运动的不同的动态品质。几种典型的趋近律为:等速趋近律,指数趋近律,幂次趋近律,一般趋近律。

2.1 新型趋近律的提出

为了解决传统指数趋近律滑模控制超调量大,收敛速度慢等问题,本文结合文献[15]的思想对变结构控制中的指数趋近律进行改进,并将状态变量|x|引入趋近律中,其具体形式为:

(4)

式中:ε>0,1>γ>0,β>0结构框图如图1所示。

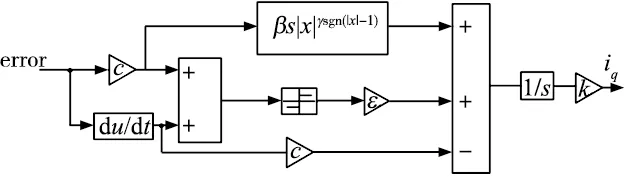
图1 新型趋近律结构框图

2.2 稳定性分析

构造Lyapunvo函数:

V=s2/2

(5)

对V求导并将式(5)代入得:

(6)

显然新型趋近律是渐进稳定的。

2.3 性能分析

对新型趋近律性能进行验证分析,考虑如下被控对象:

(7)

式中:f(θ,t)=25,b=133,取指令信号θd(t)=sin(t),被控对象初始状态为[-0.15 0.15],滑模函数设计为:

(8)

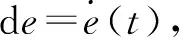
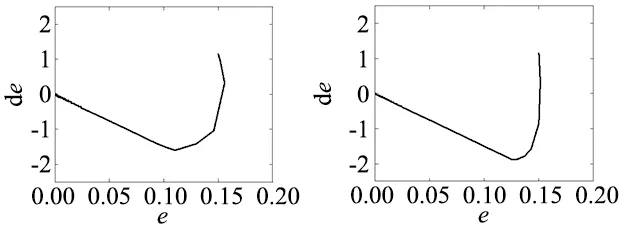
(a) 指数趋近律 (b) 新型趋近律图2 相轨迹

(a) 指数趋近律 (b) 新型趋近律图3 状态变量收敛时间

通过仿真结果可知,初始状态相同时,新型趋近律趋近滑模面的时间优于指数趋近律,状态变量收敛效果更好,收敛后波动更加平稳。

3 电流环变结构自抗扰控制器设计

自抗扰控制(ADRC)一般由跟踪-微分器(TD)、扩张状态观测器(ESO)和非线性状态误差控制率(NLSEF)3部分组成。fal函数在ADRC中起到保证系统具有快速响应的同时不会使误差过大的作用。

3.1 跟踪微分器(TD)

跟踪微分器通常情况下运用差分的方式来定义,方程为:

(9)

式中:v为输入信号,y为输出信号。

将上式离散化为:

(10)

3.2 扩张状态观测器(ESO)

最早由中国科学院院士韩京清教授提出,能够在扰动类型不明的情况下对系统受到的未知扰动进行实时估测。传统ESO通常设计为:

(11)

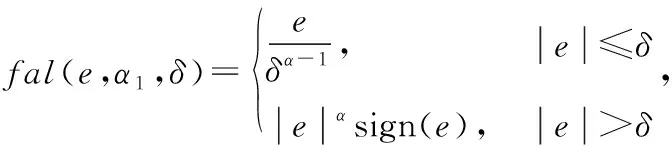
3.3 非线性状态误差控制律(NLSEF)

传统非线性状态误差控制律NLSEF实现形式为:

(12)

式中:z1、z2为ESO的状态变量,e1为给定信号的误差,e2为输出信号的误差。将所得误差经过NLSEF进行非线性组合,替代线性加权和的PI运算。

3.4 改进fal函数的交轴电流环自抗扰控制器设计

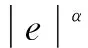
(13)

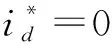
(14)

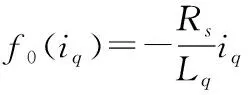
(15)

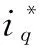
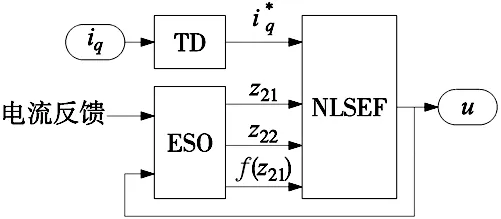
图4 ADRC结构框图

4 仿真及分析

根据以上设计,得到基于滑模-自抗扰控制的永磁同步电机矢量控制框图如图5所示。

为了验证所提控制策略的有效性和合理性,在MATLAB/Simulink环境下进行仿真实验,采用电机参数如表1所示,新型趋近律的参数为:c=180,β=500,γ=0.1,ε=10,改进型ADRC的参数如表2所示。分别采用4种不同的控制方案分析永磁同步电机的空载起动阶段、空载突变转速阶段、突加负载和突减负载阶段的性能。

表2 改进型ADRC参数

4.1 空载转速突变性能分析

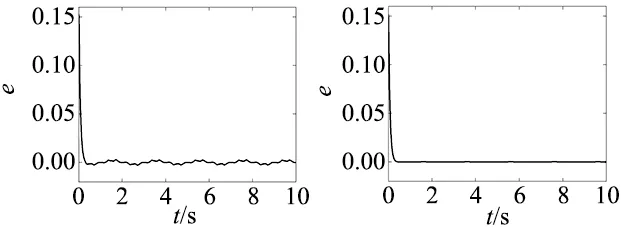
首先进行速度环新型趋近律(NRLSMC)与指数趋近律(ERLSMC)滑模控制的对比,电流环均采用传统PI控制。在空载下进行突变转速实验:电机在给定转速800 r/min空载起动,在0.2 s时突变转速为1000 r/min,仿真总时长0.4 s。转速波形如图6所示,可以看出新型趋近律极大地消除了在起动阶段的超调,但在突变转速阶段依然有较大的超调,并且变速后稳态运行阶段转速波动较大。

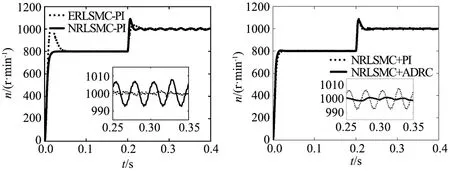
图6 转速环的两种趋近律的转速响应 图7 新型趋近律-PI与ADRC控制的转速响应

由于转速环采用新型趋近律滑模控制的系统依然有些不足,尝试将交轴电流环的PI替换为文献[14]中新型fal函数的自抗扰控制(NRLSMC-ADRC),将其与NRLSMC-PI控制方案对比,如图7所示。可以看出q轴电流环采用文献[14]的ADRC代替PI后,转速响应在变速后的稳态阶段波动大幅减小,更加稳定,但不足之处是突变转速时依然有大量超调。对q轴电流环采用本文改进后的式(13)的新型fal函数新型自抗扰控制,转速响应如图8所示。由图8可知,本文改进的自抗扰控制相比于文献[14]中的自抗扰控制应用于永磁同步电动机时,能够减弱变速时引起的超调,响应速度更快。图9为4种控制方案的空载变速的转矩响应,可知新型趋近律-新型自抗扰控制方案能够最快且以最小脉动进入稳态,变速时波动最小。

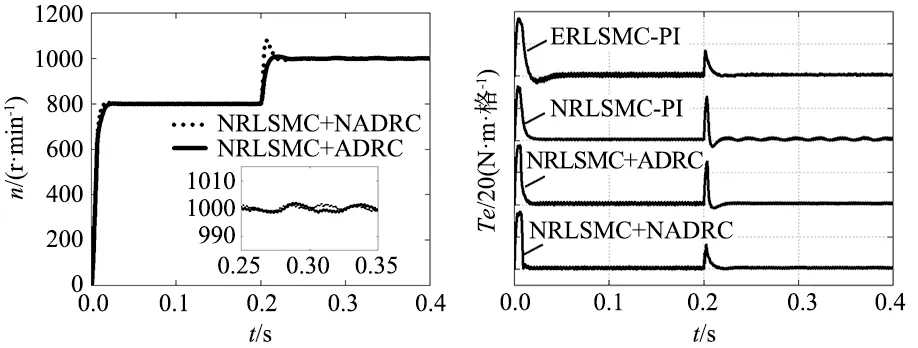
图8 新型趋近律-两种ADRC控制的转速响应 图9 空载变速转矩响应

经过以上对比,可以得出运用本文提出的转速环新型趋近律滑模控制复合电流环的新型自抗扰控制在系统空载情况下可以得到较好的响应效果。

4.2 突加突减负载性能分析

电动机空载起动,给定转速800 r/min,在0.15 s时对系统施加10 N·m的负载,在0.3 s时将负载突减为0,至0.4 s仿真结束。对4种控制方式的仿真波形对比分析,如图10、图11所示,可以看出,突加、突减负载的情况下,传统滑模控制器下的系统抖振最大,新型趋近律(NRLSMC-PI)能削弱一部分抖振,当电流环采用文献[14]提出的ADRC时,抖振得到进一步削弱,NRLSMC-NADRC控制方案下系统抗负载扰动性能最强,抖振量小,具有更快的响应速度。因此本文针对永磁电机矢量控制转速环和电流环的改进方法可以有效提高调速系统的控制品质,降低了系统的电磁损耗。

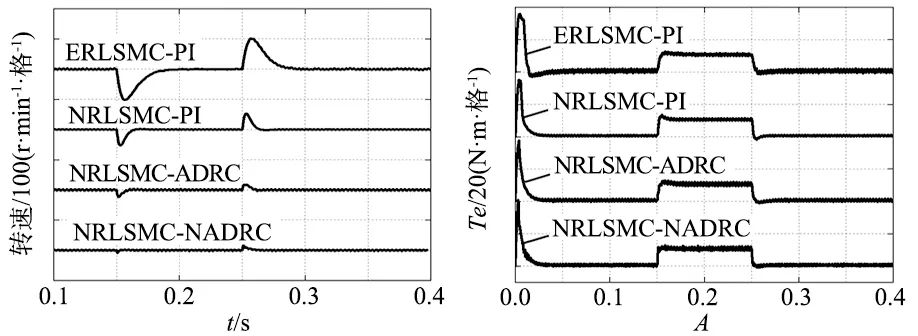
图10 负载扰动下转速响应 图11 负载扰动下转矩响应

5 结束语

本文在指数趋近律滑模控制基础上引入了系统状态变量,提出一种新型趋近律滑模控制器,并将电流环PI控制替代为改进fal函数的自抗扰控制器。并将该方案在变速、外部负载扰动等复杂工况下与其他方案进行仿真对比,仿真结果表明此控制方法具有较强抗干扰能力,能有效地抑制抖振,能克服传统滑模控制快速性与超调不能兼得的问题,因此能够提升永磁同步电动机的控制效率、改善调速性能。