透水鱼礁型潜堤内部流场及绕流特性模拟
2023-08-02匡翠萍郑宇华顾杰韩雪健
匡翠萍, 郑宇华, 顾杰, 韩雪健
(1.同济大学 土木工程学院,上海 200092;2.上海海洋大学 海洋生态与环境学院,上海 201306)
近年来,在国内外大力提倡效法自然的工程设计理念背景下,新兴的环境友好型海岸防护建筑物——鱼礁型潜堤应运而生。鱼礁型潜堤将人工鱼礁的设计融合到离岸潜堤的结构中,这一概念最早由Armono和Hall[1]提出并通过试验证明了这两类构筑物结合设计使用的可行性。我国一直致力于提升海域、海岛和海岸带的环境和生态价值。自2010年起,我国京津冀旅游胜地北戴河为修复侵蚀严重的海岸开展了一系列的灾害治理工程,工程岸线长度3.5km,工程后海岸修复成效显著。值得注意的是,在工程中首次采用了鱼礁型潜堤代替了传统的堆石离岸堤应用于海岸恢复治理,改善了近岸海域的生态环境,增加了渔业资源[2]。鱼礁型潜堤多设计为空心的透水结构,投放于工程海域中礁体内部和周围会形成连续多变的流场形态,能够迎合不同海洋生物对水流条件的趋向性[3],兼具生态修复和改造流场的效果。鱼礁型潜堤形成的流场本质上体现了复杂的钝体绕流现象,包含了高度非线性的湍流流动过程,如流体分离和涡旋演化,这类问题往往难以得到解析解,却又是准确评估鱼礁型潜堤产生的流场效应和生态效应的重要依据[4]。
至今,已有众多学者利用物模试验和数值模拟方法研究了鱼礁型潜堤绕流流场特性。吴建[5]基于ADV测流结果分析了不同来流速度下方体礁型潜堤周围的流场变化,分别采用重整化群k-ε(Renormalization Groupk-ε)和可实现k-ε(Realizablek-ε)湍流模型模拟计算了单体箱型人工鱼礁的绕流特征,结果表明2个湍流模型对礁体周围的涡旋结构都有一定的预测能力,而可实现kε模型在流线曲率变化较大的地方比重整化群k-ε更准确一些。Li等[6]通过重构的k-ε湍流数学模型和PIV测流技术分析了圆管型人工鱼礁周围上升流的强度和尺度,发现上升流的强度和尺度随着鱼礁数量的增多而增大,当礁高与水深比值为0.224时,鱼礁组合产生的效应更强。王者也和李爽[7]使用并行大涡模拟模式(Parallelizeda Large-eddy Simulation Model, PALM)及示踪物模型,研究了不同流速条件下方型鱼礁型潜堤对流场形态和湍流动能收支的影响。崔勇等[8]和胡聪等[9]均采用水槽试验和重整化群k-ε湍流模型分析了不同纵横布设间距对圆筒形礁体流场的影响,得到上升流体积随礁体横纵向布设变化的规律。Tang等[10]根据氢气球试验结果对比了3个双方程k-ε模型(标准k-ε、重整化群k-ε和可实现k-ε模型)对方体人工鱼礁流场的适用性,发现标准k-ε(Standardk-ε)模拟结果与试验得到的礁体外流场中的流线变化基本一致。Maslov等[11]以不规则多功能人工鱼礁为研究对象,将双方程k-ε、k-ω(ω为比耗散率[12],μt=ρk/ω)模型以及剪切应力输运模型(Shear Stress Transport, SST)模拟得到的礁体周围流速分布与ADV测量结果进行对比,发现以单调迎风格式离散的k-ω模型计算结果与实测值吻合最好。Kim等[13]基于粒子图像测速(particle image velocimetry,PIV)的试验结果,比较了标准k-ε、重整化群k-ε、k-ω、SSTk-ω和雷诺应力(Reynolds Stress Model,RSM)模型在半球形人工鱼礁流场模拟中,礁体尾流的规模和位置的不同,发现RSM模型能够最准确地预测鱼礁尾流的规模和位置,然而RSM模型的计算时间明显高于其他另外4种湍流模型,计算量大且难以收敛,因此在工程中不常采用。近年来越来越多学者关注鱼礁型潜堤的绕流流场特性,大多数仍通过改变外界条件研究礁体周围水流结构(如上升流)的变化,而对于透水鱼礁型潜堤流场中湍流扰动最复杂的部分,即礁体内部的流动分离特征尚未有详细讨论。针对鱼礁型潜堤的数值计算,由于每种湍流模型基于的各种假设和包含的经验常数都具有一定局限性,可以看到各家研究中湍流模型的采用不单一且不唯一,根据特定水流条件下结构物的不同,湍流模型的选择也可能不同。从已有的研究成果可以看出,双方程湍流模型已经能够基本刻画鱼礁型潜堤周围的紊流情况,其中以双方程标准k-ε和重整化群k-ε模型应用最为广泛。随着计算机技术的飞速发展和计算流体力学的精度要求不断提高,大涡模拟也被更多地应用于结构-流体相互作用形成绕流流场的精细化研究,其在复杂的鱼礁型潜堤绕流流场内精确求解某个尺度上所有的湍流运动体现了很大的优势。可见,目前对于鱼礁型潜堤周围绕流流场的预测可选的模拟方式较多,可根据不同的环境条件选择不同的湍流模型,而对于鱼礁型潜堤内部紊流场的刻画方式目前仍未有足够的研究成果支持统一定论。
本文以北戴河生态修复工程中投放的透水鱼礁型潜堤为原型,通过合理比尺制作试验模型,采用PIV技术对单体鱼礁型潜堤模型进行测流试验,分析鱼礁型潜堤内部和周围形成的绕流流场特征。基于有限体积法,建立与PIV试验相同的数学模型,分别采用3个双方程k-ε模型(标准k-ε、重整化群k-ε、可实现k-ε)和大涡模拟对鱼礁型潜堤的绕流流场进行数值模拟,通过对比计算与实测得到的流场分布和礁体内外的涡旋结构分析这4种湍流模型的准确性和适用性,为进一步了解和优化其在海洋生态修复工程领域的应用提供参考。
1 水槽试验
试验在上海海洋大学水动力学实验室的循环水槽中进行, 水槽试验段长6.00m、宽0.45m、高0.55m,水槽底板及侧壁均为钢化玻璃,便于开展PIV流速测量,具体如图1a所示。水槽系统采用循环方式供水,进口处底部为蜂窝状钢板,具有整流和消除大尺度涡结构的作用,进水段壁面向直道段沿曲线收缩,使得水流流速沿下游方向单调增加,保证了水体进入试验段后流态平稳。基于目标投放海域水深(约7m)和实验水槽尺寸,将鱼礁型潜堤按几何比尺1:12.5进行模型设计,材料为亚克力有机玻璃,透光率为92%,模型长L=0.214m、宽B=0.152m、高H=0.224m,模型的顶板和迎流面上均开有4 个直径为0.024m的圆孔,如图1b所示。考虑到鱼礁型潜堤的实际投放情况,北戴河海域平均流速约为0.3m·s-1,工程区内流速基本小于0.10 m·s-1[14],因此,在本试验中,经均匀流测试后,将进口流量设置为40 m3·h-1,相应入口平均流速为u0=0.091 4 m·s-1。鱼礁型潜堤模型放置于水槽中央,距离入水口3m,水深为0.27m。试验中雷诺数为18 121,属高雷诺数的湍流。
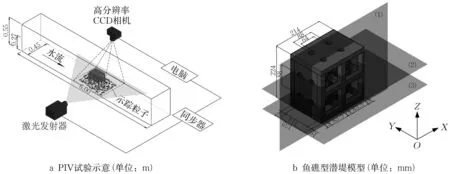
图1 PIV试验及鱼礁型潜堤模型示意Fig.1 Schematic diagram of PIV test stand and reef-type breakwater model
流速测量采用美国TSI公司研发的粒子图像测速系统,连续记录礁型潜堤近区瞬时速度场的时间序列数据,并计算出反映流场特性的速度剖面及相应的紊流脉动数据。PIV系统主要包括示踪粒子、光学照明系统、图像记录系统和图像处理系统4个部分。示踪粒子采用聚氯乙烯微粉(PVC-6500),具有跟随性好、化学性质稳定的优点。照明光源采用双脉冲激光器,片光厚约2 mm;图像记录系统主要通过高频CCD相机(分辨率为2 048×2 048像素)连续曝光,在不同时段拍摄鱼礁型潜堤近区流场的粒子图像,采样频率为4.83Hz,即每秒获得4.83对PIV图像,进而得到4.83个速度场的数据。所得流场图的后处理通过PIV系统自带的Insight 4G软件,基于互相关算法[15]对粒子速度场图中的流速矢量进行拟合计算。研究表明,人工鱼礁周围的三维涡结构在由展向涡和流向涡组合而成,在垂向和水平向上差异显著[16]。因此,试验选取了3个不同位置的剖面进行流速测量,激光光源首先从水槽上方向下投射,激光垂直穿过礁体顶板的一列圆孔;随后调整激光器位置,分别使激光水平穿过礁体迎流面的上、下2排圆孔,利用CCD相机依次捕捉激光照亮的粒子图像得到3个剖面的流场图,即图1b鱼礁型潜堤中的剖面(1)、(2)和(3)。每个剖面的测流每次连续捕捉500个瞬时流速场,然后将瞬时流场数据进行平均,得到时均流场图,并获得相应的流场参数。
2 数学模型
2.1 模型设置
模拟采用的鱼礁型潜堤规格与PIV试验中的一致。计算域尺寸的设定根据PIV试验中水槽的尺寸和礁体潜堤模型的尺寸综合决定。在数学模型中,将计算域的宽度设定为水槽宽度0.45m,计算域的高度设定为水深高度0.27m,计算域的长度则根据单体鱼礁型潜堤的尺寸进行设定,为16倍的礁体长度(礁体前方5倍,礁体后方10倍),以确保礁体后方尾流区的范围能达到10倍的礁体尺寸。
因多孔透水鱼礁型潜堤结构较为复杂,采用非结构网格对鱼礁型潜堤进行网格划分,如图2所示。鱼礁型潜堤壁面和底部壁面与水流的交界处存在边界层,边界层很薄,但是其中的各项流体参数却发生着剧烈的变化,存在较大的速度梯度。为准确模拟礁体近区的绕流流动,将近壁边界层第1层网格厚度设为0.5mm,变化率为1.1,对鱼礁型潜堤迎流面、礁顶及透水圆孔内壁进行局部加密。数值计算结果的准确性很大程度上取决于网格的数量和质量。为减小数值模拟过程中由于网格尺度所引起的误差,首先针对网格数量无关性进行了研究,并保证网格质量都在同一水平,通过改变模型表面和周围网格的大小来确定最优的网格数。考虑到不同湍流模型对网格划分及密度的要求不一样,大涡模拟模型对网格要求最高,因此以大涡模拟模型计算结果为参考,依据Biron等[17]的方法进行网格无关性验证,确定最合适的网格全局尺寸,即当不同网格模型的计算结果相近时,90%流场点的误差控制在5%以内,可以认为计算值与真实值比较接近。以最密网格(网格数量360万)为基准计算不同网格数量下的标准差,结果如表1所示,网格在97万时即已经达到了网格独立性要求,过密的网格对流场最高流速的精确度没有明显的提高。基于流固交界面的流动特性分析,综合考虑模型的计算时间和计算精度,采用网格总数为112万时确定的全局网格尺寸。

表1 网格无关性验证Tab.1 Verification of grid independence
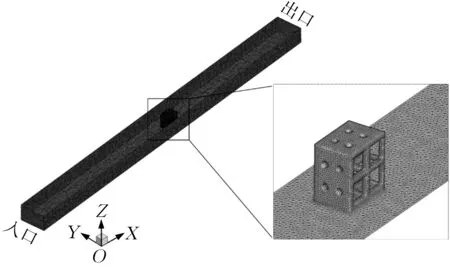
图2 数值水槽及鱼礁型潜堤模型网格划分示意Fig.2 Schematic diagram of computational domain and the grids distributed near a single reeftype breakwater
网格无关性标准差为
式中:Xi为第i次最大流速Umax;δ为第i次之后所有Xi的标准差;n为次数;g为重力加速度。
计算域边界条件设置为:入口边界条件选择速度入口,流速根据水槽试验的实际测量值给定; 出口边界条件选择压力出口,平均静压P为零;鱼礁型潜堤个体及水槽壁面均设置为无滑移固壁边界,并采用无滑移边界条件;由于鱼礁型潜堤在淹没状态下水面较平稳,自由水面采用刚盖假定处理,设置为对称边界(在进行鱼礁型潜堤结构周围和内部水力特性研究时,主要观察其内部和周围的流场,而其水面起伏及水位变化对研究结果影响不大,考虑到计算资源及计算时间,采用刚盖假定对其表面进行处理)。
根据鱼礁型潜堤近区水流运动的特性,将流体假设为不可压缩、定常、黏性流体,采用有限体积法离散控制方程,基于压力求解器,压力-速度耦合方式采用SIMPLE算法,压力项采用二阶方法离散,单元中心梯度插值方法采用基于单元体的最小二乘法插值。
2.2 湍流模型
鱼礁型潜堤近区形成的绕流是空间上不规则和时间上无秩序的非线性湍流流体运动。湍流数值模拟可分为直接数值模拟和间接数值模拟,前者直接求解Navior-Stokes(N-S)方程得到有效的湍流信息,但由于N-S方程本身求解的复杂性和巨大的计算量,现有的计算资源往往难以满足高雷诺数流动直接模拟的条件,因此限制了其应用范围。为简化计算过程使工程计算具有可行性,通常对湍流做某种程度的近似处理以简化N-S方程进行间接数值模拟,主要手段包括雷诺平均法(Reynolds Average Navier-Stokes,RANS)和大涡模拟法(Large Eddy Simulation,LES)。RANS模型通过引入雷诺应力和湍流模型实现对N-S方程的间接求解,在鱼礁型潜堤工程湍流问题中得到广泛应用的模式是引入双方程k-ε湍流模型。由于各湍流模型的差异,其结果存在差异,因此根据试验结果对引入不同湍流模型的RANS模型和LES模型进行分析比选,以获得合适的湍流模型和参数。
2.2.1 基于RANS的双方程k-ε湍流模型
对于不可压缩流体,其瞬态控制方程为
式中:ui为i方向的速度分量;xi为i方向的坐标分量;xj为j方向的坐标分量;t为时间;ρ为流体密度;P为压强;ν为运动黏滞系数;fi为作用于单位质量水体的体积力。
对瞬态控制方程进行雷诺平均,得到时均形式的控制方程为
标准k-ε模型是标准的双方程湍流模型,是由Launder和Spalding[18]通过实验现象总结出来的半经验公式,其输运方程可整理如下:
k方程为
ε方程为
式中:k为紊动能;ε为紊动耗散率;Gk为湍流应力或速度梯度引起的k的产生项;Dk为k的耗散项;μ为动力黏滞系数;μt为涡黏系数;ρ为密度;σk、σε、Cμ、C1ε、C2ε和C3ε均为经验常数或改进的变量,具体取值可参考文献[19]。
标准k-ε模型假定流场为完全湍流,忽略分子之间的黏性,将涡黏系数假定为各向同性的标量,故其只对完全是湍流的流场有效,并非适用于任何流动。因此,许多学者进一步对其改进,提出不同的假设修正k-ε模型,并由此发展出许多衍生的k-ε模型。
重整化群k-ε模型是Yakhot和Orszag[20]采用重整化群数学方法对k-ε模型进行改进后的湍流模型,通过在大尺度运动和修正的黏度项体现小尺度的影响,使这些小尺度运动有系统地从控制方程中去除。重整化群k-ε模型的k方程与标准k-ε模方程中的k方程一样,但ε方程增加了一项Rε,其源项为计算方法为
同时,在ε方程产生项的系数C*2ε的计算中引入了主流应变率,这样在重整化群k-ε模型中C*2ε不仅与流动情况有关,而且在同一问题中也是空间坐标的函数。
可实现k-ε模型是20世纪末由Shih等[21]提出的带旋流修正的k-ε模型,与标准k-ε模型相比有2个主要的不同点:一是在模型中为湍流黏性增加了一个公式,湍流黏性系数仍由式(5)确定,但是Cμ不再是常数,而是与k、ε和旋转应变率U*有关的函数,即
二是耗散率ε输运方程不同,为耗散率ε增加了新的传输项,这个方程来源于一个为层流速度波动而作的精确方程,更适于表达能谱的传输[22]。可实现k-ε模型较前2种k-ε模型的优点是可以保持雷诺应力与真实湍流一致,对涡旋流计算、带压强梯度的边界层计算和分离流计算等问题的处理可以更符合实际情况。
2.2.2 大涡模拟
湍流由不同尺度的涡旋组成,湍流的脉动与混合主要由大尺度涡造成,小尺度涡的主要作用是耗散紊动能。大涡模拟以特定的分辨尺度将流动分解为大尺度运动(大于网格尺度)和小尺度运动,对大尺度湍流运动直接用N-S方程求解,而对于小尺度湍流运动通过构建亚格子模型封闭于求解方程组中。不同尺度流动的区分依靠滤波函数来实现,对不可压缩N-S方程在物理空间过滤得到的控制方程为
式中:xi、xj为坐标分量为滤波后的流速分量为滤波后的压强;τij为亚格子尺度雷诺应力,代表过滤掉的小尺度脉动和大尺度脉动之间的能量运输。为了使方程闭合,采用Boltzmann假定的涡黏模型求解亚格子应力,为
3 结果分析
3.1 流场分布
图3为利用PIV技术测量得到的单体鱼礁型潜堤近区在垂向上和水平向上3个不同位置剖面的时均流场图,通过在流场图中加入流线的方式更清晰地展示鱼礁型潜堤近区的紊流形态。由图3a可以看出,由于礁体的阻水作用,水流行至鱼礁型潜堤前方沿着礁体迎流面抬升,在礁体上方形成了明显的上升流,最大流速达到0.106m·s-1,较入流速度增加了18%。上升流从鱼礁型潜堤顶板流过,顶板阻力沿程消耗水流的能量,导致贴近顶板的流速较小。流过鱼礁型潜堤顶板的水流,因礁体后没有了礁体占有的固体空间,水流向下跌落,流线向下,形成了较大的逆时针回旋流,即背涡流,并从背流面底部再次进入礁体。显然,鱼礁型潜堤内部水流主要来自从鱼礁型潜堤后方进入的背涡流,礁体内平均流速较入流速度减小约70%。鱼礁型潜堤迎流面和顶板都有透水圆孔,部分水流透过迎流面圆孔进入鱼礁型潜堤,产生了类射流效应,在礁体内部形成了2个条状的较高流速区(vxz≥ 0.058 m·s-1),该区内射流方向与主流方向一致。背涡流底流绕过礁体内方柱流向迎流面,受自迎流面圆孔进入的水流干扰,被分割形成上下2对涡旋。同时,由于礁体内部流速小,鱼礁型潜堤顶部上方流速大,在礁体顶板附近产生了虹吸效应,导致部分水流从顶板圆孔流出,使鱼礁型潜堤内部的水体与礁顶上方的主流发生交换。

图3 水槽试验结果及特征断面位置示意Fig.3 Experimental results and the locations of specific cross-section for validation of the numerical models
图3b和图3c分别为穿过迎流面近底部(Z=48mm)和近表面(Z=136mm)2排圆孔的水平流场。水流经过鱼礁型潜堤时,主流过水断面束窄,在礁体两侧分离形成高流速带(vxy≥ 0.116 m·s-1)流向下游,并在礁体后方背涡流区域内形成了一对水平展向涡。由于孔隙透水,在鱼礁型潜堤内部也形成了大小不一的涡旋。在鱼礁型潜堤迎流面后方靠近两侧边界处,受水槽两侧高速水流的影响,礁体内、外流体的强力剪切作用最显著,流速沿鱼礁型潜堤两侧边界的法向变化剧烈,因此在近底部和近表层流场中都出现涡旋,且该处的涡旋结构在不同高度的水平截面上基本一致。近表层流场比近底部流场形成更多涡旋,这是因为近表层截面与鱼礁型潜堤顶板的距离小于近底部截面与水槽底部的距离,近表层水流受礁顶壁面影响更大,消耗了更多水流能量。同样地,在垂向流场中,礁体内上半部也产生了更多涡旋,与水平流场情况一致。
为考察不同湍流模型对流场中速度矢量计算结果的精确性,将对流场中不同位置的特征剖面中的纵向流速进行比较。基于PIV试验结果,提取鱼礁型潜堤近区不同特征断面沿程的纵向流速,垂向上为穿过礁顶圆孔中心线和背流面的A1—A1、A2—A2和A3—A3;横向上为穿过礁体前后隔间的中心线C1—C1和C2—C2;纵向上为穿过鱼礁型潜堤迎流面圆孔的中心线S1—S1和S2—S2,具体位置如图3所示。图4对比了实验测量值与4种湍流模型的模拟结果。图4a、4b、4c为3个垂向截面的纵向流速分布图,其中位于鱼礁型潜堤内部的A1—A1和A2—A2截面的流速峰值都出现在迎流面透水孔正后方,这也验证了由于孔隙透水在礁体内部产生的射流效应,导致该处水流紊动最为强烈。在A1—A1断面,各湍流模型对纵向流速变化趋势的预测与试验测量结果基本一致,根据断面平均流速,与实测值吻合程度的排序依次为标准k-ε> 大涡模拟> 重整化群kε> 可实现k-ε。在A2—A2断面,标准k-ε和可实现k-ε模型较准确地反映了沿程流速变化的大小和趋势,可实现k-ε稍优于标准k-ε模型,但重整化群k-ε和大涡模拟得到透水孔后方的纵向流速与实测值偏差较大,且远高于另外2个模型。在A3—A3断面,由于不再受到迎流面透水孔入流的影响,各湍流模型计算结果均与实测值吻合较好。图4d、4e为近底层水平流场2个位于中横向断面的纵向流速分布图,各湍流模型对C1—C1断面流速的计算结果显示出了较好的吻合性。对于C2—C2断面,大涡模拟的计算值出现了最大的偏差,大涡模拟得到的C2—C2断面流速变化与C1—C1的基本一致,在迎流面透水孔正后方都出现了速度峰值,而在其余模型结果中该处流速已大幅降低,无明显峰值。这由两方面原因造成,主要原因是大涡模拟水流通过迎流面透水孔后在鱼礁型潜堤内部形成的条状高流速区较其他模型结果长,可延伸至礁体内后半区,与C2—C2过流断面相交,导致C2—C2断面流速在相应位置出现了速度峰值,这在对流场做进一步分析后得到了证实(图5);其次,C2—C2断面位置恰处于2个大小相近、方向相反的涡对交界处(图3b),由于LES模型对出流断面流速的变化最敏感[23],因此在该断面下大涡模拟计算的流速变化较其他模型大。在其余的3个模型中,以可实现k-ε模型的计算值与实测值最为接近。图4f、4g为近表层流场中2个穿过迎流面圆孔中心线的纵向流速分布图,需要注意的是,在鱼礁型潜堤迎流面圆孔内的流速在试验测量和数值计算之间存在较大的差异,产生该现象的原因可能是因为在数值模型中,壁面小尺度孔结构边界的准确刻画对网格模型的要求很高,且近壁面由于边界层的存在流速变化更为剧烈,即使已针对鱼礁型潜堤模型的结构特征做了局部加密处理,但基于计算时间和计算精度综合考量下选取的网格模型可能仍难以将小尺度孔结构内部的实际流速情况精准复演。上述现象产生的原因涉及湍流模型中壁面函数的选择、边界处三维网格划分以及近壁面处理等多个方面,本文主要讨论不同湍流模型对鱼礁型潜堤内部及近区复杂湍流情况的预测能力,对这类“结构中的结构内部”,即相关鱼礁型潜堤中小尺度孔结构内流速变化的讨论分析仍存在一定局限性,未来需要对其做进一步研究予以解决。除去孔内流速外,根据平均纵向流速分布情况,对于S1—S1,各模型在纵向截面的吻合度由大到小为:标准k-ε、可实现k-ε、 大涡模拟、重整化群k-ε;对于S2—S2,为:可实现k-ε、标准k-ε、重整化群k-ε、大涡模拟。

图5 鱼礁型潜堤近区流场数值模拟结果Fig.5 Computed results of flow field in vicinity of the reef-type breakwater
3.2 涡旋结构分布
图5给出了4个湍流模型对鱼礁型潜堤流场的模拟结果,并局部放大了礁体内部的流场及其流线变化,以展示各湍流模型对鱼礁型潜堤内部水流结构的刻画结果。各模型均较好地预测了鱼礁型潜堤前方的上升流和背涡流的形态,这两者是最常用于评价鱼礁型潜堤流场效应的指标。当垂直方向的流速等于或者大于10%的来流速率时,就把该区域定义为上升流区域[6]。表2展示了各湍流模型的计算结果及计算效率,对比垂向上的最大流速可以看出,4种模型的差异很小,并且十分接近实验数据。除大涡模拟模型外,其余模型的相对误差均小于5%,其中,标准k-ε模型的计算结果误差最小。流体流过鱼礁型潜堤在其背流面形成规模最大的回流区,回流区内流向速率为负值,回流区后流体速率不断恢复至明渠流分布状态。不同湍流模型所得回流区长度不同,从图5a可以看出,各模型计算得到的垂向剖面流场图中鱼礁型潜堤后方回流区的长度各不相同。大涡模拟所得回流长度最短,而重整化群k-ε模型所得回流区最长,这与陈善群和王泽[24]的研究结论一致。受PIV试验中CCD相机分辨率的限制,本试验观测范围约为400×300mm,由于鱼礁型潜堤后方形成的回流区规模较大,本试验未能捕捉到完整的垂向回流区,但试验结果清晰显示了礁体内部的涡流结构特征和礁体后方形成的一对水平展向涡的位置。对比鱼礁型潜堤内部的垂向涡旋结构,重整化群k-ε和大涡模拟结果较试验结果偏差较大,主要差别表现在礁体内部的前半区内(迎流面中段正后方),该处流线虽出现较大变形,但仍无涡旋形成,说明上述模型对垂向分离螺旋点的预测较低,这与夏超等[25]的研究结果一致。其余2个湍流模型得到的涡旋结构分布与PIV试验结果基本吻合,但所得的涡旋数量存在不同。上述4个湍流模型中,可实现k-ε模型的计算结果在垂向涡旋分布和数量上都与实测结果最吻合。鱼礁型潜堤内部的水流结构是由高速入射流和低速缓流相互作用形成的,以连续的强旋流为主要形态特征,可实现k-ε模型引入了与旋转和曲率相关的内容,因此在涡旋结构特征明显的鱼礁型潜堤内部流场计算中体现了较高的吻合度。
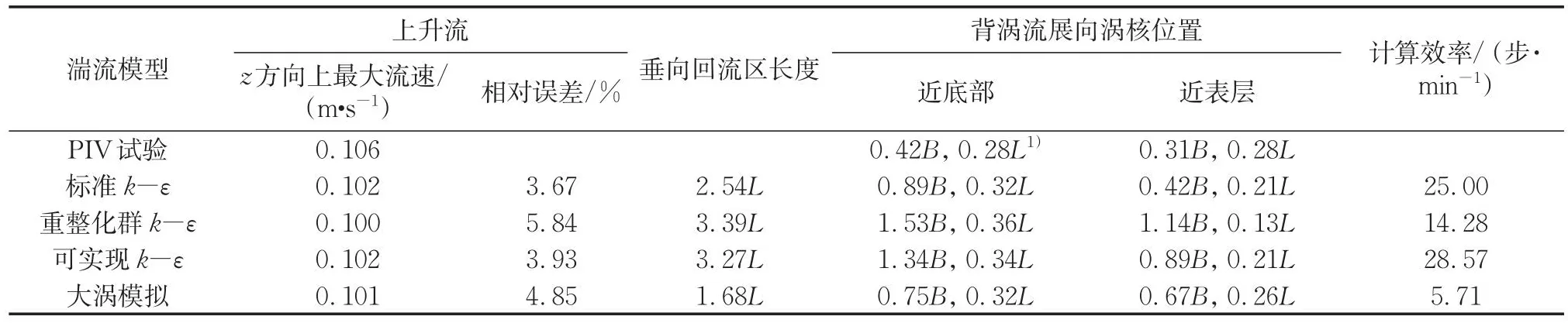
表2 各湍流模型计算结果及计算效率Tab.2 Simulated resulted of different turbulent models and their computational efficiencies
图5b和图5c分别为各湍流模型对近底部和近表层水平流场的模拟结果,鱼礁型潜堤内部和后方涡旋结构的规模和位置存在一定差异。其中,鱼礁型潜堤后方形成的一对展向涡基本以礁体纵向中轴线为对称。因此以鱼礁型潜堤纵向中轴线为基准,计算出不同湍流模型预测的礁体后方右涡核与中轴线和背流面的距离,并通过礁体外部尺寸将其量纲一化,以此来表征涡核的位置(如图3b所示),所得结果列于表2中。从表中可以看出,在近底层流场中,各湍流模型对涡核位置的预测存在不同程度的误差,其中,大涡模拟的结果误差最小,而重整化群k-ε的结果误差最大,各模型模拟得到的涡核位置距离鱼礁型潜堤背流面比实测的更长,这可能是因为试验中近底部流速较低,部分示踪粒子沉积在礁体底部,影响了近底层流场结构;而在近表层流场中,标准k-ε模拟结果与试验结果最接近,大涡模拟次之,重整化群k-ε预测效果仍最差,分析原因为重整化群k-ε中的涡黏系数μt计算公式中的系数Cμ是经验常数,可能只适用于某些流场。进一步对比礁体内部的水平涡旋结构,大涡模拟能够预测最全面的涡旋分布情况,重整化群k-ε亦能模拟得到礁体内部较多的大尺度涡旋,但流场内的涡旋分布因礁体结构而应呈现的对称性仍存在偏差;可实现k-ε模型对近底部水平流场的预测效果优于近表层,但在近表层水平流场中,仅该模型复演了与PIV测试结果一致的附着于礁体背流面方柱的2个尺度最小的角涡;标准k-ε的模拟结果误差最大,在礁体内部预测到的涡旋数量最少,在近表层中甚至表现为无涡旋流场。这是由于标准k-ε模型假定了涡黏系数μt是各向同性的标量,所以其用于模拟鱼礁型潜堤内部复杂结构引起的强涡旋流动时会产生一定的失真。
由表2 中可见,模型计算效率大小次序为:可实现k-ε、标准k-ε、重整化群k-ε、大涡模拟,由于大涡模拟模型对网格精度和计算资源的要求最高,故计算效率最低。虽然大涡模拟计算量相对于k-ε模型大,但大涡模拟方法对N-S方程直接求解大涡的优势使其对礁体近区涡旋结构的预测效果明显优于k-ε模型,尤其是鱼礁型潜堤内部和后方的展向涡对形态。双方程k-ε模型对上升流的模拟效果比背涡流更加准确,其中双方程模型以可实现k-ε模型对礁体近区的流动分离现象预测最准确,且计算效率最高。总体而言,在计算能力有限的条件下,可优先考虑使用可实现k-ε模型对多孔箱体鱼礁型潜堤的三维湍流场进行模拟计算。
4 结论
针对多孔箱体鱼礁型潜堤,分别采用水槽试验和数值模拟获得了单体鱼礁型潜堤近区的三维绕流流场和涡旋结构,结果表明礁体近区复杂的绕流流场是由不同强度的涡旋之间相互作用的结果。此外,基于试验结果,评估了4种典型的湍流模型的计算精度和效率,所得主要结论如下:
(1)试验结果表明,鱼礁型潜堤前形成了明显的上升流,最大上升流速为0.106 m·s-1,较入流速率增加了18%;背涡流在礁体后方形成,水平上呈现为一对以鱼礁型潜堤纵向中轴线为对称的展向涡对,并穿过背流面进入鱼礁型潜堤,礁内平均流速较入流速率减小约70%;水流通过迎流面圆孔以射流方式进入鱼礁型潜堤,在对应圆孔后方形成了2个较高流速区(vxz≥ 0.058 m·s-1),并对礁内水流结构起到重新调整的作用,在垂向上将内部水体分割成了上下2对涡旋,近表层由于受礁顶壁面影响更大而产生了更多涡旋。
(2)采用的4种湍流模型都能在一定精度内模拟鱼礁型潜堤绕流流场的速度分布,其中标准k-ε和可实现k-ε在纵向流速的计算上精度最高;对鱼礁型潜堤上升流的预测各模型差别不大,且都接近实测值;对于背涡流的复演,各湍流模型对涡核位置的预测都存在不同程度的误差,大涡模拟误差最小,而重整化群k-ε所得流场偏差最大;此外,双方程k-ε模型对上升流的模拟效果比背涡流更准确。
(3)礁体内部形成的涡旋结构,各湍流模型之间呈现出较大的差别。对于垂向涡旋结构,重整化群k-ε和大涡模拟对垂向分离螺旋点的预测较低,可实现k-ε模型的计算结果在垂向涡旋分布和数量上都与实测结果最吻合,且模型计算效率最高;对于水平涡旋结构,大涡模拟能够预测最全面的涡旋分布,但模型计算效率最低,标准k-ε在紊流场的刻画效果最低,可实现k-ε对近壁面小尺度角涡的刻画效果最佳。
(4)由于透水鱼礁型潜堤结构的复杂性,考虑到礁体近区绕流流动是三维的,且流态复杂,礁体内部流速很低,准确模拟存在难度。在比选的4个湍流模型中,综合模型的计算精度和效率来看,可实现k-ε是在计算能力有限的条件下最适用于多孔箱体鱼礁型潜堤近区复杂绕流流场模拟的湍流模型。
作者贡献声明:
匡翠萍:研究思路与论文结构确定、论文审阅和修改。
郑宇华:实验操作、数据处理与分析、初稿撰写与修改。
顾 杰:实验设计与指导。
韩雪健:实验操作。
