南麂列岛海域两种框型人工鱼礁水动力性能试验
2021-03-09叶功照萧云朴俞鸿源胡夫祥尤鑫星宋伟华
叶功照,王 莹,陈 舜,萧云朴,俞鸿源,,胡夫祥,尤鑫星,宋伟华
(1 浙江海洋大学水产学院,浙江省海洋渔业装备技术研究重点试验室,浙江 舟山,316000;2 浙江省平阳县海洋与渔业局,浙江 平阳,325400;3 日本东京海洋大学,日本 东京,1080075)
随着海洋渔业资源的衰退,海洋牧场作为一种生态型渔业增养殖模式是短期内恢复渔业资源的重要举措[1]。南麂列岛是1990年经国务院批准建立的中国首批5个国家级海洋自然保护区之一,渔业修复实践已进行了30多年并卓有成效。但经过基于计算回波角瞬时图像技术的侧扫声呐技术(C3D)对南麂列岛海域5个海区人工鱼礁的位置及布局、礁体稳定性、礁体沉降情况等进行侧扫探测分析,南麂列岛所建礁体普遍存在沉陷、移位等现象,建设效果没有达到预期的目标[2]。对南麂列岛所布设的人工鱼礁进行相应的水动力性能分析研究很重要[3-4]。
目前,国内对于人工鱼礁水动力性能的研究方法较常使用的有水槽模型试验[5-7]、粒子图像测速水槽试验[6-8]及数值模拟试验[8-13]。水槽模型试验以其直观、真实的特点而在国内外得到了快速发展。史红卫等[14]通过水槽试验对无盖礁体和有盖礁体在不同迎流角度下的水动力性能进行对比研究。张硕等[15-16]通过水槽模型试验对6种不同高度的混凝土鱼礁模型的流场特性进行了对比。姜昭阳等[17-18]通过水槽试验、数值模拟以及粒子图像测速技术对人工鱼礁模型各断面压力分布、流场效应以及礁体的受力情况进行对比验证。佐藤修等[19]通过水槽模型试验研究了4种不同形状鱼礁的水动力性能和其他系数。总体上,对框型人工鱼礁在不同迎流角度与迎流速度的水动力性能尚缺乏研究。
利用水槽模型试验,对传统的与改良后的两种框型礁体在不同水流速度和迎流方式时的水动力和安全性能进行比较研究,探讨礁体结构的改变对水动力性能的影响,为进一步改良人工鱼礁的稳定性与防沉陷性能研究提供参考。
1 材料与方法
1.1 试验模型
实物礁体有两种(礁体A和礁体B,见图1)。
都是以钢筋混凝土为材料,查询水力学表糙率为nf=0.014[20-22]。礁体A为边长3 m的正方形框型鱼礁,棱柱宽0.3 m,礁体内部加入框架结构,框架棱柱宽0.3 m;礁体B以礁体A为基础,底部再加高1 m,加高部分棱柱宽0.3 m,各棱柱末端以平板连接,平板长3 m、宽3 m、厚0.2 m,平板中心为1 m×1 m的镂空,相比礁体A,礁体B既增加了礁体底面积,减缓了礁体淤泥底质环境的沉降速度,同时还增加了礁体高度,可保证沉降过程中礁体的有效高度。

两种礁体的实物与模型参数见表1。

表1 两种礁体的实物与模型参数
1.2 水槽试验条件
试验在东京海洋大学(TUMST)的大型回流水槽中进行。水槽的观测部长9.0 m、宽2.2 m、水深1.6 m,水流速度可由变速装置控制,可以在0~3 m/s之间变换。其中,鱼礁模型试验均在中层水域进行,以减弱流体池壁效应与自由表面效应的影响。试验时采用螺旋式流速计来测量流速,六分力测力仪来测量模型的升力与阻力。图2为测量系统示意图。
1.3 研究方法
1.3.1 水槽模型试验
对A、B两种礁体模型,测量其在水平方向迎流角度为0°、15°、30°、45°时(图3),按照雷诺相似准则计算出0.15、0.20、0.25、0.30、0.35 m/s时的水动力性能。在稳定流速时,采集阻力值与升力值。
1.3.2 阻力系数与雷诺数的计算方法
礁体的迎流面积A:
A=P(cosθ+sinθ)
(1)
礁体的阻力系数Cd:
(2)
礁体的雷诺数Re:
(3)
式中:A为礁体迎流面积,m2;P为礁体正面迎流时的投影面积,m2;Cd为阻力系数;F为阻力,N;ρ为海水密度,一般取1 025 kg/m3;u0为海水流速,本试验中即为水流速度,m/s;Re为雷诺数;d为特征长度,m;v为运动黏性系数,m2/s。两种礁体的实物与模型迎流面积见表2。

表2 两种礁体的迎流面积
1.3.3 实物礁体作用力计算方法
人工鱼礁礁体在一定流速下的流体作用力可分为拖曳力Fd和附加质量力Fm两部分,可以用数学形式表示成流速与流速导数的函数关系。根据中村充[23]的研究,在无波浪的条件下,礁体所受的作用力F就等于拖曳力Fd:
(4)
式中:Cd为阻力系数,取礁体在流场中达到自动模型区时的值,需要从试验中得出;ρ为海水密度,一般取1 025 kg/m3;A为礁体的迎流面积,m2。计算出的礁体作用力与实际测得作用力比较,根据中村充的研究[23],模型礁体所受的作用力FM与实物礁体所受作用力FS的比值与流体密度、迎流面积、海流速度有关:
(5)
式中:ρS为海水密度,一般取1 025 kg/m3;ρM为水槽中的水密度,一般取1 000 kg/m3;AS为实物礁体迎流面积;AM为模型礁体迎流面积,m2;u0S为实物礁体的迎流速度,m/s;u0M为模型礁体的迎流速度,m/s。
1.3.4 礁体安全性校核计算公式
礁体在水流冲击下不发生移动,即礁体不滑动,要求礁体与海底接触面间的静摩擦力大于流体作用力。静摩擦力与最大流体作用力的比值称为抗漂移系数S,该数值必须大于1,才能保证礁体不发生滑动或漂移[24]。
礁体的抗滑移安全性校核计算公式为:
(6)
式中:W为礁体所受重力(N),其中,礁体A所受重力WA=148 204 N,礁体B所受重力WB=207 288 N;ω0为海水密度,取1 025 kg/m3;σG为鱼礁材料密度,取值1 900 kg/m3;μ为鱼礁与底质摩擦系数,一般情况下取0.5;F为礁体作用力,由式(3)得出。
礁体在波流作用下不发生翻滚,这就要求礁体的重力和浮力的合力矩M1大于波流最大作用力矩M2,M2与M1的比值称为抗倾覆系数S,该数值必须大于1,才能保证礁体不发生倾覆[25-26]。
礁体的抗倾覆安全性校核计算公式为:
(7)
式中:L为翻转中心到礁体中心的水平距离,m;h0为流体作用力的作用高度,m。
吴子岳等[27-28]研究认为,结构简单且对称的礁体可假设L为其边长的1/2,F为礁体作用力由式(3)得出,h0为礁高的1/2。
1.4 试验数据处理
由于水槽试验中不可避免的会产生一定的误差,此次水槽试验采用求取平均值的方法来作为水槽试验的最终试验结果。并将试验结果代入式(4),以求得礁体在不同流速、冲角下的作用力,计算得出抗滑移系数与抗倾覆系数。
2 水动力试验结果与分析
2.1 礁体阻力与流速的关系
流速是影响礁体所受作用力的重要因素。针对两种礁体、4种迎流方式,所测得的阻力与流速的关系如图4与图5所示。从两图中可以看出,不论是模型礁体A还是B,均能反映出人工鱼礁模型的水阻力随着流速增大而增大的规律,且两者的变化趋势基本相同。
当迎流角度为0°、15°、30°、45°时,在5种流速(0.15、0.20、0.25、0.30和0.35 m/s)下,模型礁体B比A的水阻力分别高34.50%~51.49%、29.39%~40.10%、35.96%~43.16%、40.30%~45.06%、25.84%~30.33%,平均高40.95%、33.43%、38.72%、42.49%、27.67%。从平均差值可以看出,两种模型礁体在迎流速度v=0.35 m/s时阻力差值明显小于其他迎流速度下的阻力差值。
通过回归分析,模型礁体A与B的阻力与流速的关系相似,礁体所受阻力与迎流速度的关系呈幂函数关系。从幂函数关系式种可以看出,在迎流角为0°、15°、30°、45°时,模型礁体B幂函数关系式的系数与指数都要比A的大;且A与B的幂函数关系相似,即都在冲角θ=30°时系数最大,指数随冲角递增而递减。
2.2 礁体阻力与冲角的关系
冲角也是影响礁体所受作用力的重要因素。针对两种礁体、5种迎流速度,所测得的阻力与流速的关系如图6所示。从图6中能反映出人工鱼礁模型的水阻力随着冲角增大而增大的规律,这与唐衍力等[29]的研究结果相似,且两者所有速度随冲角的变化趋势基本相同,即:角度越大上升的斜率越低。无论是哪一种迎流方式,模型礁体B所受阻力都要大于A。
当迎流速度为0.15、0.20、0.25、0.30和0.35 m/s时,在4种迎流角度(0°、15°、30°、45°)下,模型礁体B比A水阻力分别高30.33%~51.49%、27.94%~43.55%、25.84%~41.04%、26.58%~40.30%,平均高42.03%、36.82%、34.22%、33.55%。从平均差值可以看出,两种模型礁体的阻力差比值随冲角递增而递减。
2.3 礁体阻力系数与雷诺数的关系
模型礁体A与B在不同迎流角度下的阻力系数和雷诺数关系曲线如图7所示。
可以发现两种模型礁体阻力系数与雷诺数的关系在4种迎流方式下都相似。当阻力系数Cd随着雷诺数Re的增加基本保持稳定,即可认为进入自动模型区域[30]。因此,当两种礁体模型在迎流方式为θ=0°时,模型礁体A的阻力系数Cd=2.03,B的Cd=2.10,其自动模型区域为Re>3×104;当两种礁体模型在迎流方式为θ=15°时,模型礁体A的阻力系数Cd=2.13,B的Cd=2.13,其自动模型区域为Re>3.20×104;当两种礁体模型在迎流方式为θ=30°时,模型礁体A的阻力系数Cd=2.22,B的Cd=2.22,其自动模型区域为Re>3.25×104;当两种礁体模型在迎流方式为θ=45°时,阻力系数随着雷诺数Re的增加在试验范围内仍处于递减的趋势,因此对后三点采用插值法并估计自动模型区域为Re>4×104,所得模型礁体A的阻力系数Cd=2.18,B的Cd=2.16。
2.4 礁体的阻力系数与冲角的关系
模型礁体A和B的阻力系数与冲角的关系如图8、图9所示。
均能反映出阻力系数随冲角增大而增大的规律,但在大部分情况下,当冲角θ>15°后随着冲角变大,其上升的效率降低,甚至在迎流速度v=0.35 m/s、冲角θ=45°时的阻力系数比θ=30°时的还要低;在数值上,各流速下礁体的阻力系数在冲角15°时差异最小,在冲角θ=45°时数值差异最大。
3 实物礁体安全性能校核
3.1 礁体作用力计算
将模型礁体A和B通过试验所测得的在迎流速度v= 0.35 m/s时的阻力值与实物礁体的计算阻力值、冲角在0°、15°、30°、45°时的结果进行比较(表3),可以发现两种礁体的实际阻力值小于计算阻力值。模型礁体A的相对误差小于3%,差异不大;模型礁体B的相对误差约6%,差异较大。
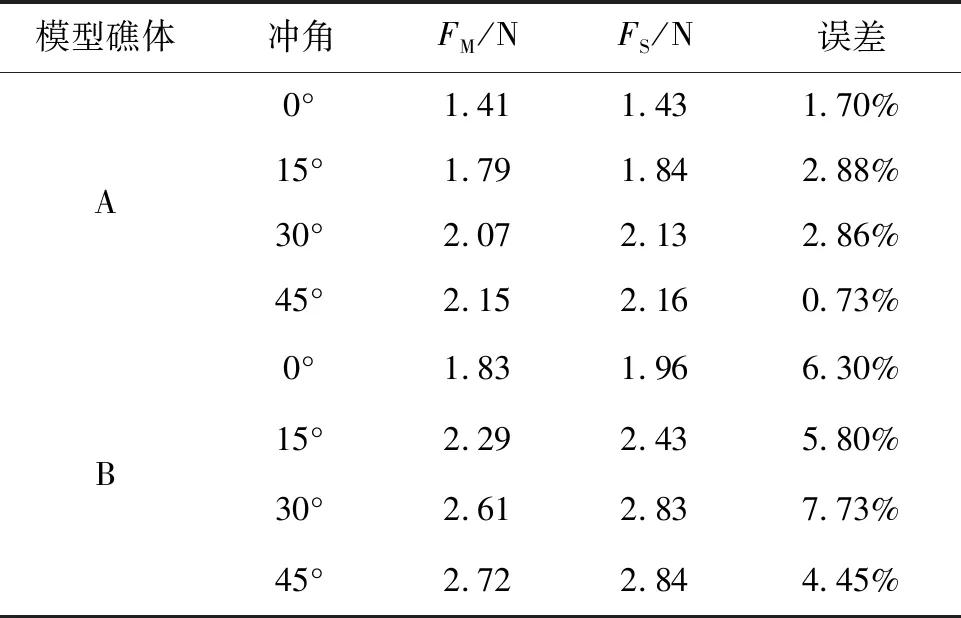
表3 两种模型礁体的试验阻力与计算阻力结果比较
3.2 礁体抗滑移的安全性分析
实物礁体A、B的抗滑移系数计算结果见表4、表5。可以发现,礁体A与礁体B在实际冲角0~45°之间、海水流速≤3节时,S值均远>1.2,是相当安全的[31];当海水流速=4节、冲角≥30°时,1 表4 实物礁体A抗滑移系数 表5 实物礁体B抗滑移系数 实物礁体A和B的抗倾覆系数计算结果见表6、表7。可以看出,两者均反映出抗倾覆系数随着冲角增大而增大的规律,但由于抗倾覆系数皆大于1.2,因此可以判断,礁体A、B在此海域不会发生倾覆。 表6 实物礁体A抗倾覆系数 表7 实物礁体B抗倾覆系数 通过水槽试验和安全性分析,探究框架型人工鱼礁的水动力性能。在礁体高度增加40%及底部结构改变的情况下,两种礁体的阻力系数在相同雷诺数时相似;两种礁体在不同工况的阻力均与流速呈幂函数关系;低流速时阻力系数随冲角增加而增加,可能是超过一定流速、冲角时,形状对阻力的影响超过了黏性对阻力的影响,这还需进一步研究。改良后礁体抗滑移、抗倾覆能力与改良前相似,但底部结构的改变,使得改良后礁体的防沉陷性能更加突出,达到了改良的目的。但是,底部结构与礁高的改变是否会带来流场效应的改变,尚未研究,今后将使用数值模拟相关软件进行比较研究。 □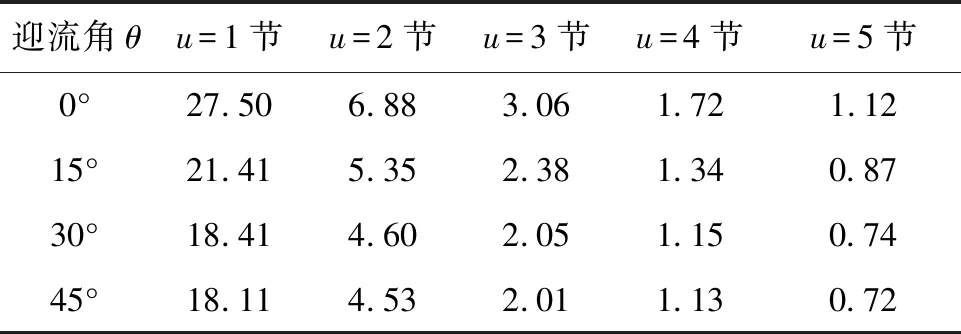
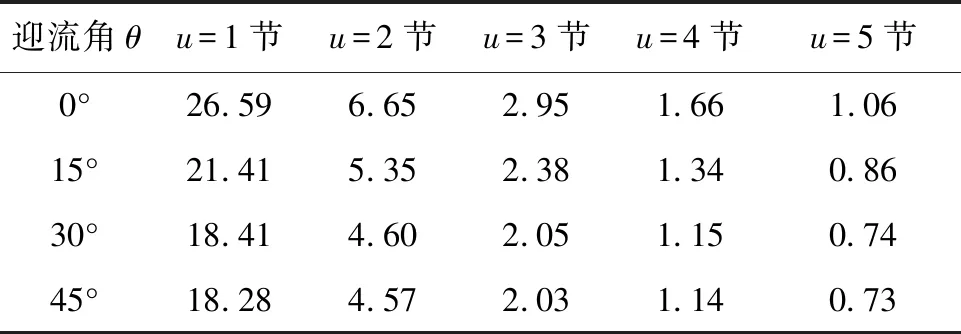
3.3 礁体抗倾覆安全性分析

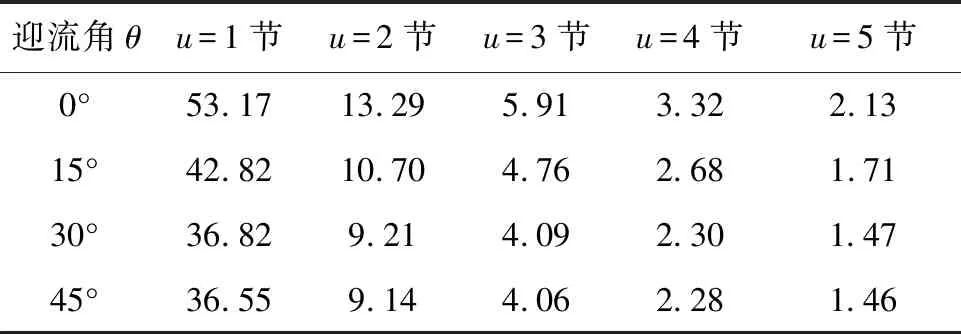
4 结论
