总弯沉比及其在机场刚性道面板底脱空判定中的适用性

凌建明， 刘海伦， 马正好， 唐龙

（1.同济大学 道路与交通工程教育部重点实验室， 上海 201804；2.同济大学 民航飞行区设施耐久与运行安全重点实验室， 上海 201804；3.民航专业工程质量监督总站华东地区监督站 ，上海 200335；4.民航机场规划设计研究总院有限公司， 辽宁 沈阳 110041）

板底脱空是机场刚性道面中普遍发生的一种病害。大量研究表明［1-3］，脱空板在荷载作用下板内应力急剧增加，易引发道面断板、错台等病害，严重影响机场道面使用寿命和服务水平，威胁飞机运行安全，因此，及时、准确地发现板底脱空、适时采取预防性养护措施，对有效控制道面结构损坏、保障机场道面使用性能和服役寿命具有重要意义。

目前，国内外最普遍的板底脱空检测技术是弯沉检测。基于弯沉判定板底脱空，评价指标的选取最为关键。自20世纪80年代以来，国内外学者提出了多种弯沉指标用于板底脱空判定，如荷载中心弯沉值、弯沉盆曲线特征、同板弯沉差、弯沉比、荷载—弯沉曲线截距值等［4］。相较于公路刚性路面，机场刚性道面结构形式更为多变，因而，能够考虑道面结构差异的弯沉比法和截距法在民航领域内得到普遍应用。如我国民航推荐采用弯沉比法［5］，而欧美国家则推荐采用截距法［6］。然而，在实际工程应用中，截距法存在板底脱空时的零截距问题［7］，而弯沉比法则难以区分板底脱空与接缝传荷对弯沉的耦合影响［4］，严重影响机场道面板底脱空评价结果的准确性。因此，寻找一种适用性更好的板底脱空判定弯沉指标显得尤为迫切和必要。

既有研究多着眼于单块板，极少同时考虑接缝两侧道面板，实际上无论是板底脱空判定还是接缝传荷能力评价，都与接缝两侧的道面板紧密相关，因而可同时反映接缝两侧道面板状况的弯沉指标就显得尤为重要，其中较具代表性的是接缝两侧弯沉之和（sum of deflections on two sides of joints，SD）。SD在基于Winkler地基假定进行分析时，有一项重要特征——“接缝两侧弯沉之和等于自由板边弯沉”，即SD与接缝传荷能力无关。自20世纪八九十年代开始，SD的这一特征被广泛应用于刚性道面性能评价［8-9］。此外，文献［10-12］基于美国NAPTF(National Airport Pavement Test Facility）现场试验结果研究发现，即使应用SD的前提（面层板与基础完全接触［13］）不成立，实测的SD仍然不受道面接缝传荷系数波动影响。这表明，SD在避免接缝传荷影响评价道面性能方面具备一定优势。

为此，本文借鉴弯沉比指标构建方法，基于SD构建总弯沉比（total deflection ratio，RTD）这一指标，并采用有限元建模计算分析RTD对道面结构参数、接缝传荷能力及脱空参数等的敏感性，同时与目前机场常用板底脱空判定弯沉指标进行对比，分析RTD在机场刚性道面板底脱空评价中的适用性。

1 总弯沉比的提出及其特征

1.1 总弯沉比的提出

道面板弯沉受荷载参数、道面板结构参数及基础参数等多种因素影响，为降低上述因素对弯沉的影响，借鉴弯沉比指标的构建思路，构建新的弯沉指标——总弯沉比。

式中：RTD为总弯沉比；Dcenter为板中位置荷载中心弯沉值；Dsum为与板中测试同荷载级位下的接缝两侧弯沉之和，以图1传感器布置为例，Dsum即为D2传感器测试值与D3传感器测试值之和；DLoad和DUnload分别为板边或板角测试时接缝两侧等距离处受荷板和未受荷板的弯沉值，对应图1中D2传感器测试值和D3传感器测试值。

图1 传感器布设位置（单位：cm）Fig.1 Layout of sensors position(unit: cm)

以我国机场道面测试常用的落锤式弯沉仪（Falling Weight Deflectometer，FWD）为例，承载板直径30cm，传感器布设位置如图1所示。测试时以FWD分别测试同一块板的板中、板边中点和板角位置的弯沉：板中测试时承载板中心位于道面板几何中心处；板边测试时承载板位于板边中点并需保证距荷载中心最近的2个传感器（图1中D2、D3）跨缝布置；板角测试时尽可能靠近板角，传感器跨缝布置与板边测试类似。各位置测试示意如图2所示。

图2 FWD弯沉测试位置Fig.2 Layout of FWD measurement points

按照上述方法确定板中、板边或板角的测试位置，具体弯沉测试操作要求可参照《民用机场道面现场测试规程》（MH/T 5110—2015）［14］执行，不再赘述。

1.2 总弯沉比特征理论分析

对Winkler地基上设接缝的2块板，基于接缝仅传递弯矩和剪力、接缝两侧道面板结构完全对称、道面板与基础完全接触等假定，Guo［13］推导证明了板边荷位的接缝两侧弯沉之和等于自由板边弯沉。对板角荷位，侧边约束影响可视作荷载按一定比例折减，对最终结论并无实质性影响。因此，可将总弯沉比简化为自由板板角、板边与板中不同荷位的弯沉比值进行分析。

对于Winkler地基上无限大板或半无限大板，当圆形荷载分别作用于板角、板边及板中时，Westergaard给出了各典型荷位的最大弯沉计算式［15］如式（3）—（5）。

板角荷位弯沉：

板边荷位弯沉：

板中荷位弯沉：

式中：wc、we、wi分别为圆形荷载作用自由板板角、板边及板中道面相应荷位的最大弯沉；P为荷载；kc、ke、ki分别为板角、板边及板中处基础模量；r为道面相对刚度半径；u为道面泊松比；a为圆形荷载半径。由此可得板角总弯沉比和板边总弯沉比计算式为

式中：RTD，c、RTD，e分别为板角总弯沉比和板边总弯沉比。

需要说明的是，式（6）和式（7）是以板角荷位和板边荷位最大弯沉推导所得，与1.1节所述RTD测试所需特定位置的板角弯沉或板边弯沉结果略有不同，但组成形式一致。为便于分析，仍以式（6）和式（7）为例进行阐述。

圆形荷载半径a及道面板泊松比u均可视为定值，则式（6）和式（7）均由两部分组成：第一部分为相应荷位与板中荷位的基础模量比，第二部分为道面相对刚度半径r的复杂函数。由此可知，RTD仅与板底脱空（基础模量k）和道面结构参数（道面相对刚度半径r）相关，不受接缝传荷能力影响。当道面板底无脱空时，有kc=ke=ki，RTD是仅与道面相对刚度半径r有关的函数；对确定道面结构，当道面板底发生脱空时，有ki＞kc或ki＞ke，此时RTD值必大于无脱空道面RTD值，且板底脱空越严重（kc或ke越小），RTD值越大。此亦即基于RTD评价道面板底脱空的基本原理。

2 适用性分析方法

2.1 适用性分析原则

弯沉指标在机场刚性道面板底脱空判定中的适用性分析主要包括3个方面：①弯沉指标随道面结构参数的变化趋势；②弯沉指标随接缝传荷能力的变化趋势；③弯沉指标随脱空参数的变化趋势。为直观分析构建的总弯沉比的适用性，将目前常用的脱空判定弯沉指标即弯沉比和截距作为对比研究对象。

弯沉比是我国《民用机场道面评价管理技术规范》（MH/T 5024—2019）中推荐的板底脱空判定指标，其测试计算方法为：采用FWD分别测试同一板块板中、板边中点和板角位置的弯沉（荷载中心值），计算“板边中点弯沉除以板中弯沉”和“板角弯沉除以板中弯沉”2项指标，并依据表1判定板底脱空状况。表中，Dedge为板边荷位荷载中心弯沉值；Dcorner为板角荷位荷载中心弯沉值。

表1 机场刚性道面板底脱空状况判定标准［5］Tab.1 Criteria for detecting void of airport rigid pavement[5]

截距法是美国FAA（Federal Aviation Administration）咨询通告AC 150/5370-11B中推荐的板底脱空判定方法［6］，其测试计算方法为：在道面板边中点或板角处采用多级荷载测试表面弯沉，以荷载值为纵轴、弯沉值为横轴作图，并以荷载-弯沉最佳拟合直线在横轴（弯沉轴）上的截距值作为板底脱空判定指标，一般认为当该截距值大于3mils（约76μm）时即发生板底脱空。

道面结构参数主要考察道面面层厚度、面层板弯拉弹性模量以及基层顶面反应模量，而这三者对弯沉指标的影响可综合为道面相对刚度半径r这一指标进行分析，r计算方法见式（8）：

式中：u为泊松比；h为道面面层厚度；E为面层板弯拉弹性模量；K为基层顶面反应模量。

接缝传荷能力是指道面接缝传递荷载的能力，一般采用接缝传荷系数LTE（load transfer efficiency at joint）表征，其常用的基于弯沉比传递系数表示的计算方法如式（9）所示：

式中：ELT为接缝传荷递系数。

脱空参数方面主要考察脱空形式和脱空范围变化对指标的影响。脱空形式包括接缝单侧脱空、接缝双侧不对称脱空和接缝双侧对称脱空3种形式，考察不同脱空形式及荷载作用位置对指标的影响；脱空范围主要指脱空区域的平面面积，考察指标与脱空范围间的相关性。

2.2 有限元模型构建

采用大型通用有限元软件Abaqus进行建模计算。模型构型采用与弯沉比法和截距法相同的Winkler地基上单层板形式。研究表明［16］，当以道面弯沉为分析对象时，对板中、板边和板角不同荷位分别采用2块板、2块板和4块板模型即可获得足够计算精度。因此，统一采用4块板模型。道面板平面尺寸采用机场道面常用的5m×5m，密度2 400kg·m-3，泊松比0.15。

道面相对刚度半径r在机场道面所常见的0.7～1.4m之间选取，其值通过调整h、E、K获得：①我国运输机场绝大多数为C类以上［17］，根据设计要求，C类以上机场K值不低于80MN·m-3，本文在80～300MN·m-3间选用；②板厚h在机场道面常用的32～42cm间取值；③E值变化对r影响很小，按机场道面设计常用值取37GPa。

道面板间接缝传荷能力通过板间设置剪切弹簧并改变剪切弹簧刚度模拟，根据试算结果设置10%～90%共计9种不同接缝传荷系数。不考虑接缝宽度。

荷载采用FWD测试荷载。根据FWD常用传感器布置确定荷载中心位置及分析点位。鉴于以静载代替动载计算结果误差不足5%［16］，本文选用静载分析。为获得较高质量的有限元网格，将FWD圆形荷载作用面（半径0.15m）近似等效为边长0.3m的正方形；荷载级位按机场道面测试要求［14］，截距法采用100kN、140kN两个级位，弯沉比法及总弯沉比法均采用140kN。

板底脱空通过移除脱空区板底基础模量模拟。板角脱空区设为正方形，板边脱空区设为沿板边全长分布的矩形。双侧不对称脱空通过固定一侧脱空宽度（0.5m）、改变另一侧脱空宽度模拟不同工况；3种基本脱空形式根据荷载作用位置又可拓展为单侧-荷载位于脱空区（V1L1）、单侧-荷载位于未脱空区（V1L0）、双侧不对称-荷载位于变动脱空区（V2UL1）、双侧不对称-荷载位于固定脱空区（V2UL0）、双侧对称（V2S）5种不同形式。不同脱空范围通过改变脱空区宽度（0.25～1.50m）模拟。

在模型单元类型选取方面，C3D8I在沿厚度方向包括4个及以上单元时，应力和挠度均可以获得稳定的收敛结果且计算代价较小［18］，因此选用C3D8I作为模型基本单元，并在厚度方向划分4层。模型单元基本平面尺寸取25cm，在荷载作用范围及重点分析区域适当加密。

综上共计建立800个模型进行计算分析。

3 结果分析

3.1 道面结构参数变化影响

在接缝传荷能力不变（ELT=60%）、板底无脱空的条件下，调整h、E、K获得41种不同道面相对刚度半径r，分析不同弯沉指标随r变化规律。结果如图3～5所示。

图3 道面相对刚度半径对弯沉比的影响Fig.3 Effect of relative stiffness radius on deflection ratio

对比图3和图4可知，随r变化，弯沉比和RTD并不固定。以板角为例，随着r变化，弯沉比变化率约为18.8%，RTD变化率约为12.4%。表明弯沉比和RTD均无法避免道面结构参数带来的影响。但是，弯沉比随r增加并不单调增加，二者间并无明显相关性；而RTD与r之间则存在较高的关联性，以二次函数拟合，判定系数R2可达0.9左右，这与RTD特征的理论分析结果相符。因此，在无法避免道面结构参数影响的前提下，RTD这一特点为建立精确判定标准提供了可能。

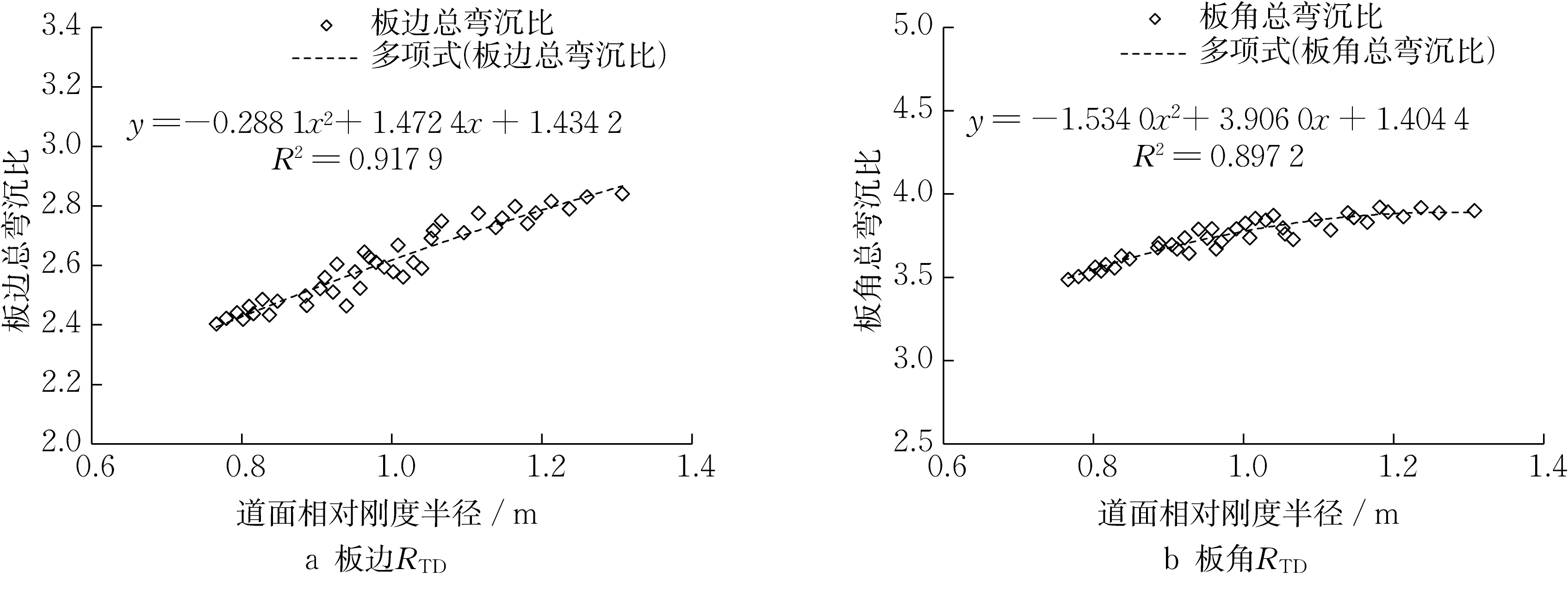
图4 道面相对刚度半径对RTD的影响Fig.4 Effect of relative stiffness radius on RTD

图5计算结果显示，当r变化时，不同荷位截距值均在零附近，即截距这一指标并不受道面结构参数变化影响。应该说，截距这一特点对板底脱空判定是有利的。然而，后续结果表明，以截距判定道面板底脱空的理论依据可能并不成立。

图5 道面相对刚度半径对截距的影响Fig.5 Effect of relative stiffness radius on intercept

3.2 接缝传荷能力变化影响

机场水泥道面纵缝一般为设拉杆的平缝或企口缝［19］。研究表明［20-22］，相比假缝，其接缝传荷能力较高且稳定。因此，将纵缝接缝刚度设为定值，考察横缝传荷能力变化对各指标的影响。计算结果如图6～8所示。

图6 ELT对弯沉比的影响Fig.6 Effect of ELT on deflection ratio

图6表明，ELT由10%增加到90%，板边弯沉比减小了40.1%（2.28到1.37）；而板角弯沉比则减小了41.0%（3.21到1.89）；表明接缝传荷能力变化对弯沉比影响显著。此外，由图7还可知，当板底无脱空时，以二次函数拟合弯沉比与ELT间关系，其判别系数R2接近1；这表明，对特定结构道面，以弯沉比判定板底脱空时，其判定标准应是ELT的函数，现有规范中推荐的以接缝传荷能力等级选用判定标准具有合理性；但由于脱空与接缝传荷的耦合影响（见3.3节分析），其标准选用的准确性有待商榷。

图7 ELT对RTD的影响Fig.7 Effect of ELT on RTD

由图7可知，随着ELT变化，板边RTD、板角RTD均保持稳定，分别为2.80、3.83；这表明，RTD这一指标并不受接缝传荷能力变化的影响。结合3.1节结果，基于RTD可建立不受接缝传荷能力影响的判定标准。这一特点使得RTD在判定板底脱空时能够避免接缝传荷与脱空耦合带来的影响，在基于弯沉进行板底脱空判定时尤为重要。

图8计算结果显示，与道面结构参数类似，随着ELT变化，不同荷位的截距值均为零；截距与接缝传荷能力间并无相关关系。

图8 ELT对截距的影响Fig.8 Effect of ELT on intercept

3.3 脱空参数变化影响

根据2.2节设置不同脱空参数，考察脱空形式和脱空范围对各指标的影响。计算结果如图9～11所示（图中黑实线为无脱空计算结果）。

图9 脱空参数对弯沉比的影响Fig.9 Effect of void parameters on deflection ratio

对比图9、图10可知，不同脱空形式下，弯沉比、RTD均随脱空区宽度增大而单调增加，且二者均与脱空区宽度具有良好相关性。然而，由于同一弯沉比或RTD值可能对应不同脱空形式的不同脱空范围，这表明单纯以弯沉比值或RTD值大小并不能实现定量判定脱空。

图10 脱空参数对RTD的影响Fig.10 Effect of void parameters on RTD

对比图9与图6可知，接缝传荷能力降低和板底脱空均会导致弯沉比的增大，以弯沉比判别板底脱空时尚需考虑接缝传荷能力影响；现行方法是根据接缝传荷能力等级选取不同判别标准（见表1）。然而，大量研究证实［23-25］，板底脱空会影响接缝传荷系数测试结果；以本文不同脱空工况为例，在相同接缝刚度条件下，测试所得ELT结果相差可达20%；这种误差可能导致选用不同的弯沉比判别标准，进而造成误判。而图10和图7结果表明，RTD能够不受ELT变化影响而识别板底脱空，可有效区分板底脱空和接缝传荷能力的耦合影响，表明RTD能够更好地适用机场刚性道面板底脱空判定。

图11计算结果显示，无论脱空形式、荷载位置及脱空范围如何变化，均未出现预期截距，即截距法并不能识别板底脱空。这一结论与唐伯明［7］的室内实验结果一致。分析认为，出现这一现象的原因可能在于板底脱空并不能影响道面板在荷载作用下的线弹性变形性质，因此以截距法判定道面板底脱空的依据可能并不成立。

图11 脱空参数对截距的影响Fig.11 Effect of void parameters on intercept

4 结论

（1）基于接缝两侧弯沉之和构建了机场刚性道面板底脱空判定的弯沉指标——总弯沉比RTD，明确了RTD的测试方法；推导了RTD的解析计算式，理论分析表明RTD仅与道面结构参数和板底脱空相关。

（2）基于Winkler地基假定建立有限元模型，选取弯沉比和截距为对比研究对象，计算分析了道面结构参数、接缝传荷能力、脱空参数等的变化对RTD、弯沉比和截距的影响规律，对比分析了RTD在机场刚性道面板底脱空判定中的适用性。

（3）道面结构参数和脱空参数变化均会影响弯沉比和RTD，但RTD与道面结构参数间具有更好的关联性；随着接缝传荷能力增加，弯沉比降低，而RTD则不受影响；RTD特征的有限元计算结果与理论分析结果相吻合；截距法与道面结构参数、接缝传荷能力、脱空参数间均无相关性。

（4）由于弯沉比不能很好考虑结构参数差异与接缝传荷能力变化带来的影响，可能导致结果误判，在实际使用中具有较大局限性。以截距法判定板底脱空时，无论道面结构参数、接缝传荷能力、脱空参数如何变化，均得不到有效截距，因而截距这一指标可能无法有效判定脱空。RTD与道面板结构参数具有良好相关性，且对脱空敏感，可据此建立相对精确的判定标准；同时，RTD能避免接缝传荷与板底脱空之间的耦合影响问题，更适用于机场刚性道面板底脱空判定。

作者贡献声明：

凌建明：主要负责研究思路、架构及文稿撰写。

刘海伦：主要负责模型构建、计算及文稿撰写。

马正好：主要负责数据处理、文稿撰写。

唐 龙：主要负责数据处理、文稿校核。