2.5维有限元分析高铁荷载下弹塑性地基动偏应力与沉降

高广运， 耿建龙， 毕俊伟，3， 张继严， 徐晨晓

（1.同济大学 土木工程学院，上海 200092；2.同济大学 岩土及地下工程教育部重点实验室，上海 200092；3.广州市设计院集团有限公司，广东 广州 510620；4.重庆高速公路集团有限公司，重庆 401120）

高速铁路作为一种方便快捷的交通工具，以其高速、低排放成为各国竞相发展的交通方式。无砟轨道平顺性好、稳定性强，广泛应用于高速铁路建设中，但其对轨下路基不均匀沉降的适应性较差。我国东部沿海地区广泛分布着承载力低的软土地基，在长期荷载作用下易发生较大累积变形［1］。同时，沿海地区剪切波速较低，车速易达到轨道-路基临界速度而产生类共振现象，激发很大的振幅［2］。因此，准确计算软土地区高铁荷载下路基长期沉降已成为研究热点问题之一。

在循环荷载作用下地面沉降研究中，学者们多通过动三轴试验获得土体的偏应力来计算分析变形发展规律。温日琨等［3］基于室内不排水动三轴试验分析了交通荷载下静偏应力对饱和软黏土变形的影响。黄茂松等［4］基于上海地区第④层饱和软黏土三轴循环试验，提出考虑动偏应力水平的软黏土轴向循环塑性累积应变显式模型。姜洲等［5］在此基础上建立了K0固结条件下软黏土累计塑性应变计算公式。随着计算机的发展，一些学者建立了数值计算模型，并结合经验拟合公式计算地基沉降［6-7］。边学成等［8］通过2.5维有限元结合薄层单元方法，求解了路堤下卧层中动偏应力分布，结合累积塑性应变理论建立了列车长期运行条件下路基下卧层的动力附加沉降计算方法。董亮等［9］基于三维有限元模型计算了列车动荷载下路基内部的动偏应力，并结合路基土体累积塑性应变模型预测了列车长期循环荷载下土质路基的累积变形。

上述对地基沉降的研究均将地基模型简化为弹性介质，不能反映土体的弹塑性特征。笔者在之前研究中提出高铁荷载下弹塑性地基振动与变形的2.5维有限元算法［10］，但路基动偏应力分布和地面沉降计算仍有待进一步研究。此外，列车荷载中轨道不平顺对路基道床影响较大［11］。叶阳升等［12］研究发现有限元模型中列车静轴重乘以动力系数1.35后作为设计动荷载，计算得到的动应力与实测值偏差较小。同时，随着路基累积塑性变形的增加，轨道几何形状的不规则性加剧，也会影响轮轨接触力和地基应力分布［13］，因此有必要分析轨道不平顺等随机激振力对高铁荷载下路基沉降的影响。

基于此，本文根据弹塑性地基2.5维有限元理论，对比了考虑随机激振力前后高铁荷载下弹塑性地基中动偏应力分布规律，在此基础上根据累积塑性变形公式［5］计算了不同车速下的地基沉降。

1 列车荷载模型

如图1所示，每节车厢由1个车体、2个转向架和4个轮对等组成，则列车荷载可视为由一系列的轴重荷载组成。假定列车沿x轴正方向以速度c移动，则一节车厢运行产生的连续轴重荷载表达式为［14］

图1 列车轴重荷载分布示意Fig.1 Schematic diagram of train axle load distribution

式中：N为车厢数量；xl为列车荷载所在位置；t为列车运行时间；Pn1和Pn2分别为第n节车厢前后轮轮对轴重；Lk为第k节车厢长度；an和bn分别为第n节车体同转向架相邻轮对间距和同车不同转向架相邻轮对间距；δ为Dirac函数。

对式（1）对时间t和坐标x进行双重傅里叶变换，可得列车荷载在频域-波数域内的表达式

式中：ω为振动圆频率；ξx表示在x方向上的波数，上标“-”表示频域内的变量。当ξx=ωc时才能使荷载不为零。

目前，轮对轴重Pn多采用未考虑随机激振力和考虑随机激振力2种方式模拟。在不考虑随机激振力时，我国《高速铁路设计规范》［15］规定路基上的轨道及列车荷载可换算为一定高度和宽度的土柱（简称为准静态荷载），相应的列车荷载称为准静态列车荷载。

随机激振力非常复杂，涉及列车悬挂体系、轨道不平顺和地基的均匀性等方面。梁波等［16］提出了一个考虑钢轨、轨枕的分散传递因素，在车轮静载中增加了与高频（100～400Hz）、中频（30～60Hz）和低频（0.5～10Hz）对应并反映轨道不平顺、附加动荷和轨面波形磨耗效应的激励力，如式（3）所示。为描述方便，本文将考虑了随机激振力的轮对轴重简称为修正轮对荷载，相应的列车荷载称为修正列车荷载。

对式（3）修正轮对荷载作双重傅里叶变换［10］，可得到频域-波数域内的表达式为

式中：k1为临近车轮力在线路上的叠加系数，一般为1.2～1.7；k2为钢轨及轨枕的分散系数，一般为0.6～0.9；Q0为车轮静载；Qj=M0ajω2j（j=1，2，3）分别对应3种控制条件中振动荷载的典型值，其中M0为簧下质量；aj为相应于不平稳控制条件下的几何不平顺矢高；ωj=2πcLj为不同控制条件下的振动圆频率，其中Lj为对应的几何不平顺曲线波长；上标“～”表示波数域内的变量。当ω＞0时为“+”，当ω＜0时为“-”。

CRH380AL型列车簧下质量为M0=1 627kg，轮轴荷载为15t。Yang等［17］研究发现当车厢数量不小于4时不同列车编组数对地面振动差异较小。为节约计算时间，取列车1/2编组，即1拖7动进行计算。

2 弹塑性地基2.5维有限元模型

2.1 无砟轨道模型

无砟轨道由钢轨、轨枕、扣件、道床等组成，共同承担列车轮对轴重。在列车荷载作用下，整个轨道系统可近似为整体变形，因此将轨道系统简化为铺设在地基上的欧拉梁。

轨道的动力方程可表示为

式中：EI为轨道的抗弯刚度，E为轨道弹性模量，I为轨道截面的惯性矩；ur为轨道振动位移；mT为轨道系统综合质量；fT为地基反力；p0为外荷载。

对式（5）作双重傅里叶变换得轨道梁在频域-波数域内的表达式为

2.2 弹塑性地基2.5维有限元方程

为获得弹塑性地基的塑性位移，首先通过2.5维有限元法以弹性理论计算了土体初始位移，称为试探位移，然后根据土体的屈服情况进行塑性修正，最后通过切线刚度法获得土体表面的塑性位移。

2.2.1 求解土体试探位移

根据土体平衡方程、几何方程和物理方程，并对时间t进行傅里叶变换，可以得到三维均质弹性土体的波动方程，即频域内的控制方程为

式中：λc和μc为复数形式的拉梅常数，λc=λ(1+2βi)，μc=μ(1+2βi)，其中β为土体阻尼系数为体力；ρ为土体密度；u为土体位移。

频域内的应力边界条件为

不计体力时，对三维均质土体波动方程（7）和应力边界条件（8）应用伽辽金法，得

沿x方向进行波数展开，整理可得

式中：δu*为虚位移；δε*为虚位移对应的虚应变；上标“*”表示共轭复数。

引入形函数可得到频域内离散方程的矩阵形式为

式中：M、K和分别为质量矩阵、刚度矩阵和节点载荷列阵，分别为

式中：e表示对所有单元进行集成；J为Jacobi矩阵；N为形函数矩阵；为单元位移节点列阵ˉ为单元等效节点载荷列阵；B和D为分别为应变位移关系矩阵和应力应变关系矩阵。

采用位移协调条件耦合式（6）和式（10）可得轨道-地基的控制方程，基于VS2013平台编制Fortran程序，求解获得土体的试探位移。

2.2.2 求解土体塑性位移

获得土体试探位移后，采用改进的摩尔-库仑屈服准则式（12）［18］判断土体是否发生塑性变形。

式中：c、φ分别为土体黏聚力和内摩擦角；σm为平均应力为等效应力；θ为洛德角；K(θ)为分段函数［18］；q为反映双曲线对屈服函数的拟合程度和岩土介质抗拉强度的大小的计算参数，取值范围为［0， 1］。

若土体达到屈服条件，则通过施加体荷载pb并更新土体弹性模量来计算土体的弹塑性变形。引起应力重分布的体荷载pb在每一次迭代中均通过对包含高斯屈服点的所有单元积分求和而成。

式中：η为修正塑性矩阵DP的修正因子，由线性插值方法求得；F为屈服函数；Q为塑性势函数；De为弹性矩阵；K为划分的单元数量。

获得体荷载后，通过一致切线模量算法更新一致性刚度矩阵Dct求解土体塑性变形［19］，可表示为

式中：a和b分别表示屈服函数F和塑性势函数Q关于应力的一阶偏导数；R=Q-1De，Q=U+为单位矩阵为黏聚力关于等效塑性应变率的一阶偏导数，B为与屈服准则有关的量。

2.3 模型边界

在模型边界处设置黏弹性边界模拟波在半无限空间中的传播［20］，以黏性阻尼的吸波作用和弹簧的刚性复原作用来模拟无限空间对计算域的影响。边界单元节点上的荷载为

其在频域-波数域内的表达式为

式中：Al为节点黏弹性边界应力作用范围；Kx=Cx=Cy=kρvs，G为剪切模量，λ为拉梅常数，A为刚度调节系数，k为阻尼调节系数，r为结构几何中心到人工边界的垂直距离，vp和vs分别为P波和S波波速。

2.4 计算模型

为提高计算效率，考虑地基对称性取一半结构建模计算，建立的模型宽40.0m、深30.0m，网格尺寸控制在0.5～2.0m之间（近轨道处小、远处大）。模型左侧设置为轴对称边界，右侧设置为黏弹性边界，底部基岩层设置为固定边界，道床直接铺设于地表。根据地基设计尺寸［15］，在模型中设置荷载宽度为1.5m，道床宽度为2.0m，厚度为0.5m，轨道弯曲刚度EI为13.254MN·m2，单位质量mT为540kg·m-1，建立的计算模型如图2所示。

图2 计算模型与网格划分示意Fig.2 Schematic diagram of calculation model and meshing

2.5 模型验证

为验证弹塑性地基2.5维有限元计算模型的准确性与可靠性，分别与移动点荷载作用下弹性地基解析解和压板载荷试验结果进行对比验证。

Eason［21］推导了移动点荷载作用下弹性半无限空间振动位移的解析解。设置黏聚力为大值，使土体不会屈服进入塑性状态，将弹塑性土体退化为弹性均质土体。建立与文献［21］完全相同的计算模型，得到移动点荷载下地表下方1m深处z方向的位移响应。对计算结果进行归一化处理，数值计算结果与理论解的对比情况如图3所示。由图可知，数值计算结果与理论计算吻合较好，验证了本文理论的正确性。

图3 移动点荷载下方1m深处竖向归一化振动位移Fig.3 Vertical normalized vibration displacement value at a depth of 1m below moving point load

杨光华［22］采用压板载荷试验获得了不同荷载下的压板沉降。本文建立与该试验相同的计算模型，绘制计算结果与现场试验位移如图4所示。由图可知，当荷载小于400kPa时，计算值略小于试验值。这是由于土体为弹塑性材料，加载后产生的变形包含弹性变形和塑性变形，而当荷载较小时，采用摩尔-库仑方法判定土体单元节点未达屈服，计算得到的变形只包含弹性变形，较现场试验结果偏小。当荷载大于400kPa后，计算土体达到屈服状态，与实测位移拟合较好。总体而言，计算值与实测值拟合较好，验证了本文模型的可靠性和准确性。

图4 压板载荷试验沉降计算值与试验值对比Fig.4 Comparison of calculated and tested settlement values of pressure plate load test

3 弹塑性地基动偏应力分布及沉降计算

基于弹塑性地基2.5维有限元计算模型，高铁荷载分别考虑为准静态列车荷载和修正列车荷载后，计算加载一次后弹塑性地基中动偏应力的分布情况，并利用软黏土塑性累积应变经验模型计算2种荷载条件下弹塑性地基沉降。

考虑土体瑞利波速（93.4m·s-1）和列车设计运营时速，分别计算车速为200.0km·h-1、250.0km·h-1、300.0km·h-1、334.8km·h-1（93.0m·s-1，跨前速度）、338.4km·h-1（94.0m·s-1，跨后速度）、350.0km·h-1、400.0km·h-1时弹塑性地基的动偏应力分布情况。模型土体采用上海第②层土（粉质黏土），计算参数如表1所示。

表1 道床及土体力学材料参数Tab.1 Mechanical material parameters of ballast bed and soil

3.1 软黏土塑性累积应变经验模型

采用姜洲等［5］建立的K0固结条件下软黏土累计塑性应变公式计算地基长期沉降，如式（18）—（22）：

式中：a1、a2、a3、a4、b1、b2为拟合参数；p0为初始平均固结应力；pa=101kPa；Dd为动偏应力水平；K0为土体的侧限系数；σ′cz为求解点深度处土体的自重应力；n为求解的土体层数；γs为第s层土的有效重度；hs为第s层土体的厚度；g为计算范围内划分的土层数量；qd为动应力水平，用于判定弹塑性土体是否达到屈服条件；quit为土体破坏强度或极限强度；Mc为临界状态应力比，由固结不排水剪切试验确定；χ和κ分别为e-lgp空间正常固结和回弹线斜率；pc为初始固结平均应力；ς为初始屈服面轴线方向。

地基土模型计算参数如表2所示。

表2 模型计算参数［5］Tab.2 Parameters of model[5]

3.2 弹塑性地基动偏应力分析

3.2.1 准静态列车荷载下地基动偏应力

采用准静态列车荷载作为高铁输入荷载，计算得到单次列车荷载下土体动偏应力峰值。绘制不同车速时距轨道中心水平距离10m、深度10m范围内地基最大动偏应力分布情况如图5所示。由图可知，近轨道处等值线较密，随与轨道水平间距和深度增加逐渐稀疏，说明轨道近处动偏应力变化较大，远处变化较小。本文结果是取一半地基模型计算得到的，若考虑整个地基范围，则等值线呈马鞍形分布，与文献［23］实测路基动应力分布规律一致。在地基表面，动偏应力峰值位于距轨道中心1.5～2.0m处，这是由于本文计算模型中道床宽度为2.0m，动偏应力最大值出现在道床边缘附近土体中，与静荷载下的试验结果相同。对比不同车速时动偏应力云图的变化可以发现，车速较低时（200km·h-1、250km·h-1和300km·h-1）等值线均匀向外扩散，车速接近或大于土体瑞利波速后等值线变得复杂，这是由于车速接近和超过瑞利波速时地基中产生马赫效应［1］，在车速400km·h-1时这种现象最明显。

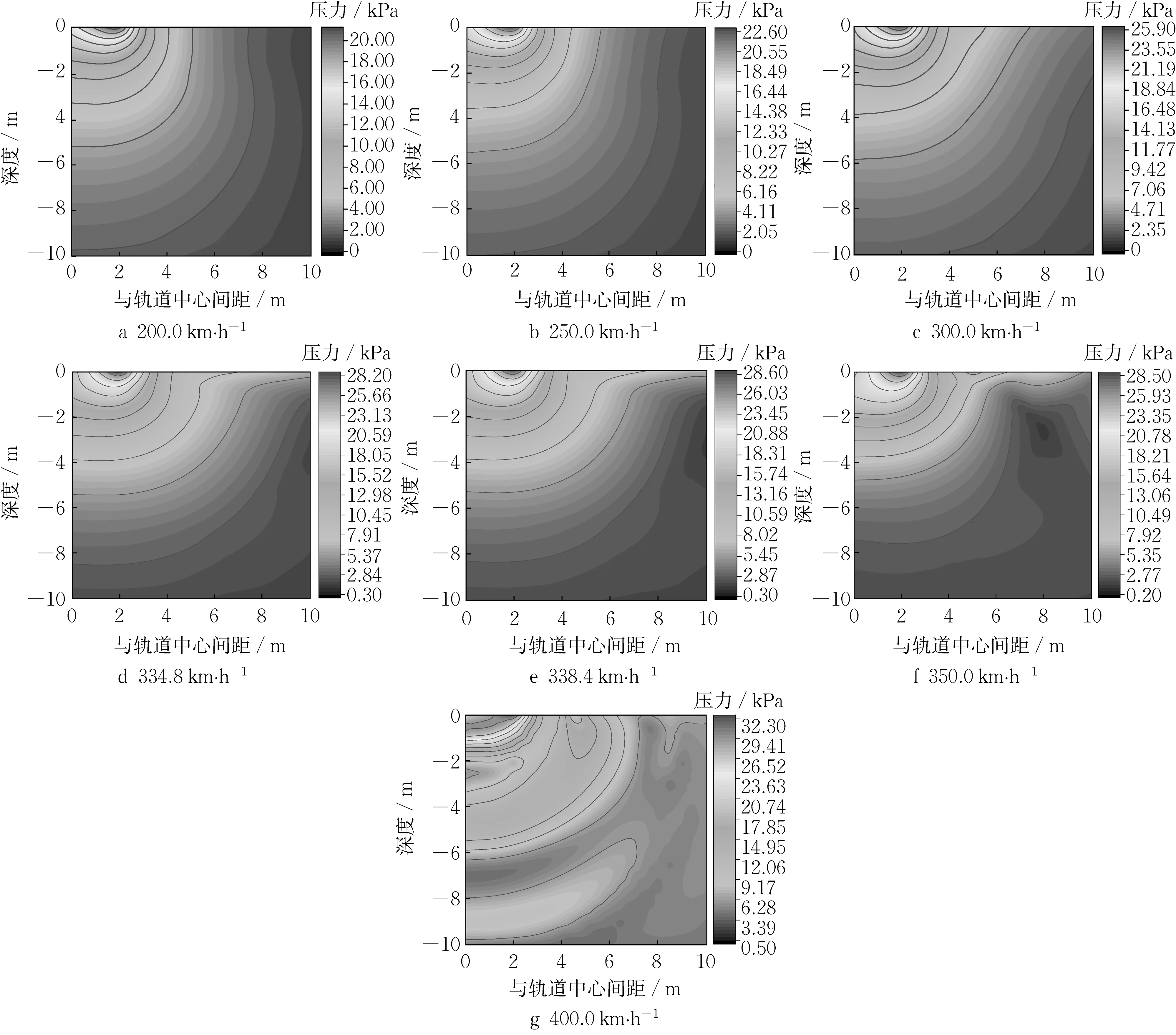
图5 准静态列车荷载下地基动偏应力云图（单位：kPa）Fig.5 Cloud diagram of dynamic deviatoric stress of foundation at quasi-static load（unit：kPa）

图6为不同车速时准静态列车荷载下地基表面动偏应力随与轨道中心间距的衰减曲线。不同车速时衰减曲线整体上均呈现先增大（距轨道中心2m范围内）后减小（距轨道中心2m外）的趋势。距轨道中心2m范围内，动偏应力随车速的增加而增大。距轨道中心2m外，车速小于土体瑞利波速时衰减曲线光滑，动偏应力随车速的增加而增大，车速接近或大于土体瑞利波速时曲线呈波动状衰减。这是由于车速接近或超过土体瑞利波速后会产生马赫效应，瑞利波传播方向与轨道呈一定夹角，而观察方向垂直于轨道方向，列车运行时前后轮对不同能量的瑞利波均通过该观察截面，前后轮轴产生的瑞利波在该截面叠加产生振动放大。

图6 准静态列车荷载下地基表面土体动偏应力衰减曲线Fig.6 Attenuation curve of dynamic deviatoric stress on ground surface at quasi-static load

图7为不同车速时准静态列车荷载下轨道中心处土体动偏应力沿深度衰减曲线。当车速小于土体瑞利波速时，动偏应力最大值出现在地表处，并沿深度光滑单调衰减。当车速接近瑞利波速时（334.8km·h-1、338.4km·h-1和350.0km·h-1），动偏应力最大值出现在距地表一定深度处（本文为0.5m），并沿深度光滑单调衰减。车速超过土体瑞利波速（400km·h-1）后，动偏应力最大值同样出现在距地表0.5m深处，在马赫效应影响下沿深度呈波动衰减。

图7 准静态列车荷载下轨道中心处土体动偏应力沿深度衰减曲线Fig.7 Attenuation curve of dynamic deflection stress of soil at track center along the depth at quasi-static load

3.2.2 修正列车荷载下土体动偏应力

将修正列车荷载作为高铁输入荷载，计算得到单次列车荷载下土体动偏应力峰值，图8为不同车速时距轨道中心水平距离10m、深度10m范围内土体动偏应力峰值云图。地基中动偏应力的分布规律与图5类似，但由于修正列车荷载中包含轨道不平顺和波形磨耗等随机激振力，弹塑性地基动偏应力值整体偏大。车速接近或超过土体瑞利波速后，在马赫效应和随机激振力的共同影响下，地基中动偏应力的分布较准静态列车荷载更加复杂。

图8 修正列车荷载下地基动偏应力云图（单位：kPa）Fig.8 Dynamic deviatoric stress cloud diagram of foundation at modified train load（unit：kPa）

考虑不同车速，图9为修正列车荷载下地基表面土体动偏应力随与轨道中心间距的衰减曲线，图10为轨道中心处不同深度处土体动偏应力沿深度方向的衰减曲线。

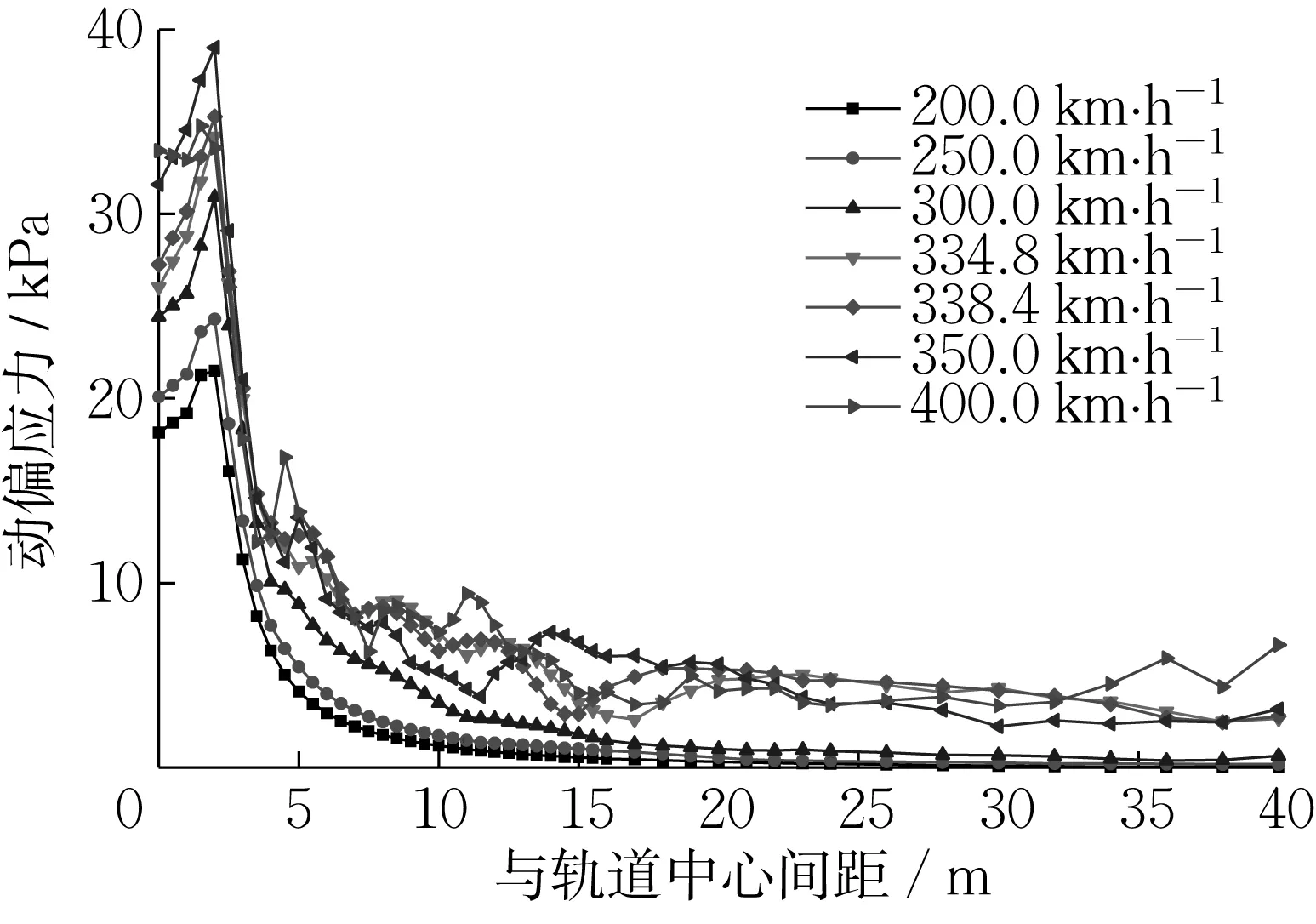
图9 修正列车荷载作用下地基表面土体动偏应力衰减曲线Fig.9 Attenuation curve of dynamic deviatoric stress on ground surface at modified train load

图10 修正列车荷载作用下轨道中心土体动偏应力沿深度衰减曲线Fig.10 Attenuation curve of dynamic deviatoric stress of soil at track center along the depth at modified train load

由图9可知，距轨道中心2m范围内，修正列车荷载下车速350km·h-1（97.22m·s-1）时动偏应力最大，出现振动放大现象，而在准静态列车荷载作用下车速400km·h-1（111.11m·s-1）时动偏应力最大（图6）。实测研究表明车速接近地基表层土体瑞利波速时会出现振动放大现象［24］，本文地基表层瑞利波速为87.93m·s-1，与修正列车荷载下的车速更为接近，说明考虑激振力后弹塑性地基中动偏应力峰值的分布更符合实际情况。

对比图9与图6、图10与图7，在2种荷载条件下，地基表面土体动偏应力衰减规律和轨道中心处土体动偏应力沿深度方向衰减规律大体一致，说明列车轮轴移动速度是影响地基中动偏应力分布规律的主要因素。同时，修正列车荷载下地基中的动偏应力较准静态列车荷载整体偏大，这是由于修正列车荷载中考虑了轨道不平顺等随机激振力，在地基中激发了更大的动偏应力［25］。

表3为不同车速时准静态列车荷载和修正列车荷载下土体动偏应力峰值。不同车速下修正列车荷载计算的动偏应力峰值均大于准静态列车荷载，当车速接近土体瑞利波速时不同荷载模型下的计算结果差异显著增大，最大达37.49%。说明不同车速条件下随机激振力对动偏应力的影响不同，在车速接近瑞利波速时对弹塑性地基的动偏应力影响最大。

表3 准静态列车荷载与修正列车荷载作用下地基动偏应力峰值对比Tab.3 Comparison of peak dynamic deviatoric stress of foundation at quasi-static load and modified train load

3.3 弹塑性地基沉降计算

交通荷载下地基 不同深度处的土体动偏应力水平差异较大，因此基于分层总和沉降计算方法，首先将地基土体划分为0.5～2.0m的若干薄层；然后基于弹塑性地基2.5维有限元模型计算得到2种荷载条件下单次列车通过时弹塑性地基土的最大动偏应力，采用式（18）—（22）计算各层累积应变；最后将所有土层变形叠加得到地基表面位移计算点（图2）的总沉降。京沪高铁日开行列车172次［26］，每列火车经过记在土体中产生一次振动，1年累积产生约6.3万次振动。基于此，考虑不同车速条件下的准静态列车荷载和修正列车荷载，计算得到路基连续加载63万次（运营10年）后弹塑性地基的沉降规律分别如图11和图12所示。

图11 准静态列车荷载作用下不同车速时弹塑性土体沉降Fig.11 Elastic-plastic ground settlement at different train speeds and quasi-static load

图12 修正列车荷载作用下不同车速时弹塑性土体沉降Fig.12 Elastic-plastic ground settlement at different train speeds and modified train load

在2种荷载条件下，路基均在投入使用初期沉降较快，随时间增加沉降速率逐渐变慢并趋于稳定。当荷载为准静态列车荷载时（图11），路基沉降随车速的增加而增大，而在修正列车荷载下（图12），车速350km·h-1时沉降最大，与偏应力峰值的变化规律基本一致。

对比2种荷载作用下地基服役10年时的沉降量可知，准静态列车荷载下沉降量均小于《高速铁路设计规范》中规定的容许值15mm，而修正列车荷载作用下车速大于300km·h-1后，10年路基沉降量均超过了15mm。因此，为了更准确计算高铁运行产生的地基长期沉降，应该同时考虑列车运行速度和随机激振力的影响。

4 结论

建立了弹塑性地基2.5维有限元计算模型，通过与Eason解析解和压板载荷试验对比验证了模型的准确性。分别考虑准静态列车荷载和修正列车荷载，对比分析了不同车速条件下弹塑性地基土体动偏应力分布规律，基于循环荷载下软黏土累积塑性应变模型计算得到高铁荷载下弹塑性地基沉降，主要结论如下：

（1）弹塑性地基中动偏应力最大值出现在道床边缘土体中。地基动偏应力呈马鞍形分布，近轨道处动偏应力的变化较大，远处变化较小。车速接近或超过土体瑞利波速后土体动偏应力变化复杂。

（2）车速是影响土体动偏应力衰减规律的主要因素。车速小于土体瑞利波速时，沿地基表面和轨道中心沿深度方向土体动偏应力的衰减曲线光滑，车速接近或大于土体瑞利波速时由于马赫效应影响动偏应力呈波动衰减。

（3）修正列车荷载下弹塑性地基中动偏应力分布较准静态列车荷载更加复杂，动偏应力峰值的分布更符合实际情况。车速接近瑞利波速时随机激振力对弹塑性地基动偏应力峰值影响最大。

（4）地基在投入使用初期沉降较快，随时间增加沉降速率逐渐趋于稳定。为准确预测高铁运行产生的地基长期沉降，应同时考虑列车运行速率和随机激振力的影响。

作者贡献声明：

高广运：指导研究开展、论文撰写及修改。

耿建龙：参与模型计算、理论分析及论文撰写。

毕俊伟：参与理论分析、论文撰写及修改。

张继严：参与模型计算、理论分析。

徐晨晓：参与理论分析、模型计算及论文撰写。